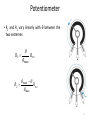* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture-7: Modeling of Real World Systems
Alternating current wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Electrification wikipedia , lookup
Opto-isolator wikipedia , lookup
Three-phase electric power wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electric machine wikipedia , lookup
Commutator (electric) wikipedia , lookup
Potentiometer wikipedia , lookup
Distribution management system wikipedia , lookup
Brushless DC electric motor wikipedia , lookup
Rectiverter wikipedia , lookup
Dynamometer wikipedia , lookup
Electric motor wikipedia , lookup
Induction motor wikipedia , lookup
Variable-frequency drive wikipedia , lookup
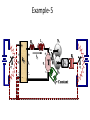
Feedback Control Systems (FCS) Lecture-7 Mathematical Modeling of Real World Systems Dr. Imtiaz Hussain email: [email protected] URL :http://imtiazhussainkalwar.weebly.com/ 1 Modelling of Mechanical Systems • Automatic cruise control • The purpose of the cruise control system is to maintain a constant vehicle speed despite external disturbances, such as changes in wind or road grade. • This is accomplished by measuring the vehicle speed, comparing it to the desired speed, and automatically adjusting the throttle. • The resistive forces, bv, due to rolling resistance and wind drag act in the direction opposite to the vehicle's motion. 2 Modelling of Mechanical Systems u mv bv • The transfer function of the systems would be V (s) 1 U ( s ) ms b 3 Electromechanical Systems • Electromechanics combines electrical and mechanical processes. • Devices which carry out electrical operations by using moving parts are known as electromechanical. – – – – Relays Solenoids Electric Motors Switches and e.t.c 4 Potentiometer 5 Potentiometer • R1 and R2 vary linearly with θ between the two extremes: R1 max Rtot max R2 Rtot max 6 Potentiometer • Potentiometer can be used to sense angular position, consider the circuit of figure-1. Figure-1 • Using the voltage divider principle we can write: eout R1 R1 ein ein R1 R2 Rtot eout max R1 ein max Rtot 7 D.C Drives • Speed control can be achieved using DC drives in a number of ways. • Variable Voltage can be applied to the armature terminals of the DC motor . • Another method is to vary the flux per pole of the motor. • The first method involve adjusting the motor’s armature while the latter method involves adjusting the motor field. These methods are referred to as “armature control” and “field control.” 8 Example-2: Armature Controlled D.C Motor Ra Input: voltage u Output: Angular velocity La B u ia eb T J Electrical Subsystem (loop method): dia u Ra ia La eb , dt Mechanical Subsystem Tmotor Jω Bω where eb back-emf voltage Example-2: Armature Controlled D.C Motor Ra La Power Transformation: Torque-Current: Voltage-Speed: B u Tmotor K t ia ia eb T J eb K b ω where Kt: torque constant, Kb: velocity constant For an ideal motor Kt Kb Combing previous equations results in the following mathematical model: dia Ra ia K b ω u La dt Jω B-K t ia 0 Example-2: Armature Controlled D.C Motor Taking Laplace transform of the system’s differential equations with zero initial conditions gives: La s Ra I a(s) K b Ω(s) U(s) Js B Ω(s)-K t I a(s) 0 Eliminating Ia yields the input-output transfer function Kt Ω(s) U(s) La Js 2 JRa BLa s BRa K t K b Example-2: Armature Controlled D.C Motor Reduced Order Model Assuming small inductance, La 0 K t Ra Ω(s) U(s) Js B K t K b Ra Example-3: Armature Controlled D.C Motor If output of the D.C motor is angular position θ then we know Ra d dt or La B ( s ) s ( s ) u ia eb J T θ Which yields following transfer function K t Ra U(s) sJs B K t K b (s) Ra Example-3: Field Controlled D.C Motor Ra Rf if ef Lf Tm J B ω Applying KVL at field circuit ef if Rf Lf Mechanical Subsystem Tm Jω Bω di f dt La ea Example-3: Field Controlled D.C Motor Power Transformation: Torque-Current: Tm K f i f where Kf: torque constant Combing previous equations and taking Laplace transform (considering initial conditions to zero) results in the following mathematical model: E f ( s ) R f I f ( s ) sL f I f ( s ) Js( s ) B( s ) K f I f ( s ) Example-3: Field Controlled D.C Motor Eliminating If(S) yields Kf Ω(s) E f (s) Js B ( L f s R f ) If angular position θ is output of the motor Ra Rf if ef Lf Tm La J B θ (s) E f (s) Kf sJs B ( L f s R f ) ea Example-4 An armature controlled D.C motor runs at 5000 rpm when 15v applied at the armature circuit. Armature resistance of the motor is 0.2 Ω, armature inductance is negligible, back emf constant is 5.5x10-2 v sec/rad, motor torque constant is 6x10-5, moment of inertia of motor 10-5, viscous friction coefficient is negligible, moment of inertia of load is 4.4x10-3, viscous friction coefficient of load is 4x10-2. La Ra ea 15 v ia N1 Bm eb T Jm BL JL N2 L 1. Drive the overall transfer function of the system i.e. ΩL(s)/ Ea(s) 2. Determine the gear ratio such that the rotational speed of the load is reduced to half and torque is doubled. System constants ea = armature voltage eb = back emf Ra = armature winding resistance = 0.2 Ω La = armature winding inductance = negligible ia = armature winding current Kb = back emf constant = 5.5x10-2 volt-sec/rad Kt = motor torque constant = 6x10-5 N-m/ampere Jm = moment of inertia of the motor = 1x10-5 kg-m2 Bm=viscous-friction coefficients of the motor = negligible JL = moment of inertia of the load = 4.4x10-3 kgm2 BL = viscous friction coefficient of the load = 4x10-2 N-m/rad/sec gear ratio = N1/N2 Example-4 Since armature inductance is negligible therefore reduced order transfer function of the motor is used. Kt ΩL(s) U(s) J eq Ra Beq La s Beq Ra K t K b La Ra ea 15 v ia N1 Bm eb T Jm BL JL N2 2 N J eq J m 1 J L N2 L 2 N Beq Bm 1 BL N2 Example-5 A field controlled D.C motor runs at 10000 rpm when 15v applied at the field circuit. Filed resistance of the motor is 0.25 Ω, Filed inductance is 0.1 H, motor torque constant is 1x10-4, moment of inertia of motor 10-5, viscous friction coefficient is 0.003, moment of inertia of load is 4.4x10-3, viscous friction coefficient of load is 4x10-2. Ra Rf ef if Lf La ea Tm Bm ωm N1 Jm BL JL N2 L 1. Drive the overall transfer function of the system i.e. ΩL(s)/ Ef(s) 2. Determine the gear ratio such that the rotational speed of the load is reduced to 500 rpm. Example-5 + + e kp r _ La Ra + ea _ N1 + ia JM BM T eb _ BL θ JL N2 - if = Constant c Numerical Values for System constants r = angular displacement of the reference input shaft c = angular displacement of the output shaft θ = angular displacement of the motor shaft K1 = gain of the potentiometer shaft = 24/π Kp = amplifier gain = 10 ea = armature voltage eb = back emf Ra = armature winding resistance = 0.2 Ω La = armature winding inductance = negligible ia = armature winding current Kb = back emf constant = 5.5x10-2 volt-sec/rad K = motor torque constant = 6x10-5 N-m/ampere Jm = moment of inertia of the motor = 1x10-5 kg-m2 Bm=viscous-friction coefficients of the motor = negligible JL = moment of inertia of the load = 4.4x10-3 kgm2 BL = viscous friction coefficient of the load = 4x10-2 N-m/rad/sec n= gear ratio = N1/N2 = 1/10 System Equations e(t)=K1[ r(t) - c(t) ] or E(S)=K1 [ R(S) - C(S) ] (1) Ea(s)=Kp E(S) (2) Transfer function of the armature controlled D.C motor Is given by θ(S) Ea(S) = Km S(TmS+1) System Equations (contd…..) Where K Km = RaBeq+KKb And Tm RaJeq = RaBeq+KKb Also Jeq=Jm+(N1/N2)2JL Beq=Bm+(N1/N2)2BL To download this lecture visit http://imtiazhussainkalwar.weebly.com/ END OF LECTURES-7 25