Download Vortex Dynamics in Bose-Einstein Condensates

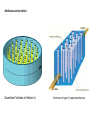
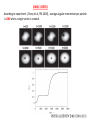
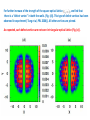
Pinning of Hidden vortices in Bose-Einstein
Condensates
Bishwajyoti Dey
Department of Physics
University of Pune, Pune.
T. M, K.P and B.D
Phys. Rev E 88, 012904 (2013)
Phys. Rev. A (R)(submitted, Feb. 2014)
T.M and K.P , Pondicherry University.
Abrikosov vortex lattice
Quantized Vortices in Helium-4
Vortices in type-II superconductors
Quantized vortices - when a quantum mechanical particle moves in a circle the
circumference of the orbit has to be an integer multiple of the de Broglie wavelength.
This “quantization rule” leads to Bohr model and discrete energy levels of the hydrogen
atom. For a rotating superfluid it leads to quantized vortices.
When normal fluid is rotated in a container, the fluid rotates as a rigid body where
the velocity smoothly increases from the centre to the edge.
Such smooth variation is not possible for particles in a single quantum state.
To fulfill the above mentioned “quantization rule”, the flow field develops singular
regions where the number of de Broglie wavelength on a closed path jumps by one.
Energetically, the most favoured configuration for this is an array of vortices. When an
atom goes around the vortex core, its quantum mechanical phase changes by 2 pi.
Creation of vortices
Liquid Helium - Rotating the Container
Quantized angular momentum - We put liquid helium in a container and rotate the
container slowly. For temperature above the lambda point (liquid helium is normal liquid )
liquid helium starts to rotate with the container and the liquid comes to equilibrium with
the container eventually.
Now, if we cool the liquid below lambda point (2.17K), the liquid stops rotating as soon as
the temperature is 2.17K, regardless of whether we stop rotating the container or we let
the container rotating.
Unlike normal liquid which is pulled along by the container and is forced to rotate with it,
the superfluid does not necessarily rotate with the container. This is because superfluid's
angular momentum is quantized.
This means the superfluid will enter into the state whose quantized angular velocity is
closest to the angular velocity at which we are rotating the container. So, unless we rotate
the container fast enough to put it into first excited state the liquid will not rotate (even if
we rotate the container). Landau 1941.
Vortices - each vortex can be thought of as a quantum of angular momentum. At the center
of the vortex is a phase singularity around which the phase changes by a multiple of 2 pi.
Phase singularity means the matter wave vanishes at the center and there is no superfluid at
the core of the vortex. Instead superfluid flows with quantized circulation around each core.
Normal component of the fluid (uncondensed component) however may be there at the core.
Creation of vortices in BEC - The situation in liquid helium is created in BEC. BEC is confined
in an asymmetries trapping potential to mimic the roughness of the liquid helium container.
The asymmetric trapping potential is then rotated which is analogous to the rotation of the
liquid helium container.
Quantized Vortices in Helium4–
velocity around vortex and number
of vortices depend on h/m.
Vortices in type-II superconductors
Quantum Vortices
Vortex Interaction - The phase circles around a vortex. The force on a vortex is in the
direction of the decreasing phase. So, if there are two vortex, they will feel a force in the
direction perpendicular to the line joining them. This force will motivate the two vortices to
either circle around each other or move parallel to each other. Magnus force.
Vortex pinning - Vortex can interact with normal component of superfluid leading to
dissipation. Vortex can also interact with defects in the system leading to vortex pinning.
Study of vortex pinning and vortex tunneling is important because of its link to the
“manipulation” of vortices. Manipulation of vortices is important for quantum
computing . Quantum vortices can become entangled. This has relevance in quantum
information and quantum computing.
Schematics of Vortex Creation
A condensate of Fermion pairs (red) is trapped in the waist of a focused Laser beam
(pink). Two additional Laser beams (green) rotate around the edges to stir the
condensate. Current-carrying coils (blue) generate the magnetic field used for axial
confinement and to tune the interaction strength by means of a Feshbach resonance.
After releasing the atomic cloud from the electromagnetic trap, the cloud expands
ballistically and inverts its aspect ratio. Resonant absorption imaging yields a density
profile of the atomic cloud containing vortices. http://cua.mit.edu/ketterle_group.
This is a picture of a rotating BEC, stirred by a laser. These sodium atoms were laser
cooled, trapped, and cooled further until they condensed into a BEC. Then the cloud of
atoms was stirred with a laser to determine whether it was in a superfluid state. One
unmistakable characteristic of superfluids is that quantized vortices form when they rotate
too quickly. The bright areas in this image are atoms in the BEC, and the dark areas are
vortices, which form in a lattice pattern as the cloud is rotated faster and faster. This
picture demonstrates unmistakably that this cloud of atoms is in a superfluid state. Martin
Zwierlein.
It has been shown that BEC trapped in rotating double-well potential (anharmonic
potential) supports “Hidden Vortices” (Wen et al, PRA 2010).
Hidden vortices do not have visible cores, but it has non-zero angular momentum.
Ghost vortices: no visible core, no angular momentum. They are formed during the
initial stage of the rotating condensate deformation.
Visible and hidden vortices
Tsubota et al, PRA 2002
Ghost vortices
Motivation
1. It is natural to ask “Like the visible vortices, can the hidden vortices be pinned “?
2. To obtain the critical rotational frequency for the rotating condensate in double-well trap.
This is motivated by the recent conjecture that “surface modes with angular momentum l=4
are excited when the rotating condensate is trapped in double-well trap”.
The critical rotation frequency
for creation of vortices have been calculated
theoretically for harmonic trap and harmonic plus anharmonic potential trap from
thermodynamic arguments (Lundh et al, PRL (2004) ) and also based on spontaneous
shape deformation (surface mode frequency) of the rotating Bose gas
(Ghosh, Phys. Rev. A (2004)).
For condensate in harmonic trap, critical rotational frequency is nearly half of the surface
mode frequency.
We show the validity of the conjecture.
Motivation
3. To obtain Feynman formula for the number of vortices for the condensate trapped in
double-well trap. Role of hidden vortices.
Feynman formula is the relation between the number of vortices and the rotational
frequency.
For the rotating condensate trapped in harmonic trap, Feynman formula shows
divergence of the number of vortices when the rotational frequency approaches
the harmonic trap frequency (Fetter RMP, 2009).
But recent experiment (Williams et al, PRL 2010) do not show such divergence.
Recently it has been suggested (Kato et al, PRA 2011) that the divergence in the number of
vortices can be avoided if one considers optical lattice with Gaussian envelope.
We show that the divergence disappears if the condensate is trapped in anisotropic
double-well trap.
4. Interesting vortex lattice structure and pinning effects the for rotating condensate trapped
in triple-well potential.
Motivation
5. The effect of three-body interaction on the vortex dynamics of the rotating condensate.
This is motivated by the observation of Efimov effect in BEC. (Efimov 1970).
Efimov Effect: There exist bound states (Efimov states) of three bosons even if
the two-particle attraction is too weak to allow two bosons to form a pair.
Borromean ring: If one ring is removed other
falls apart.
A system of atoms with attractive two-body interactions, is unstable against collapse
above certain critical number of atoms Nc. An addition of a repulsive three-body
interaction can overcome the collapse and region of stability for the condensate can be
extended beyond Nc.
The system and the Hamiltonian
The equation of motion of the condensate wave function is described by the mean-field
Gross-Pitaevskii equation
where V(r) is the trapping potential, g is the strength of the mean-field two-body
interaction and Lz = xpy –ypx is the z-component of the angular momentum operator and
is the trap rotation frequency. All the three terms plays crucial roles for the vortex
dynamics in BEC.
Vortices are nucleated when the stirring potential with low anisotropies (plays the role
of roughness of the container for creation of vortices in liquid helium) resonantly excites
the quadruple mode of the condensate and induces large amplitude oscillations of the
condensate, resulting in a dynamical instability (Sinha and Castin, PRL 2001).
The trapped BEC becomes singular when the rotation frequency is equal to or greater
than the harmonic trap frequency, since the outward centrifugal force counteracts the
inward force from the harmonic trap.
Analytical calculations – time-dependent variational analysis.
We calculate the surface mode frequency and the Feynman formula for the vortices number.
Where V(x,y) is the sum of two potentials
VARIATIONAL METHOD
To calculate the average angular momentum <Lz> per particle and its relation with the
spontaneous shape deformation of the BEC, we use time-dependent variational method.
We also calculate <Lz> numerically and compare with the variational results.
The variational wave function of the condensate is taken as
where
and
time-dependent complex variational parameters. The parameters
inverse square of the condensate widths in x and y directions and
parameter.
are
and
are
is the phase
We set
width and phase.
since we are mainly interested in the condensate
The variational parameters
can be obtained by minimizing the variational
energy with variational parameters. This gives
The coupled equations describes how the shape of the condensate changes due to rotation.
We define a parameter in terms of ratio of the widths which defines the deformation of
the condensate as
We calculate the average angular momentum per particle (<Lz> = <xpy – ypx>) as
If is equal to 2 (no deformation), then no angular momentum is transferred to the
condensate even when the system is rotating. When the frequency of rotation is increased
the system starts deforming, it starts transferring angular momentum and a vortex starts to
nucleate when the average angular momentum per particle is 1. This shows that
exist a critical angular frequency
at which the angular momentum per particle
suddenly jumps from 0 to 1.
Experimentally
has been measured and it is one when a single vortex is nucleated
(Chevy et al, PRL 2000).
Lowest energy surface mode frequency: Vortices are nucleated when the rotation excites
the quadruple mode of the condensate and induces large amplitude oscillation of the
condensate, resulting in a dynamical instability (Sinha, Castin, PRL 2001).
Using variational method we calculated the quadruple mode and surface mode frequency.
For this we take small deviations of the variational parameters from its equilibrium
values (keeping only second order deviations) and get coupled linear equations of motion
for the deviations.
SINGLE VORTEX
According to experiment (Chevy et al, PRL 2000), average angular momentum per particle
is ONE when a single vortex is created.
We obtain critical rotation frequency to create a single vortex from numerical simulation.
Critical rotational frequency agrees very well with the value
This shows the initial turbulent motion which leads to single vortex formation indeed
consist higher order surface modes with
Also , unlike the case of harmonic trap, the surface mode frequency is much smaller than
critical rotational frequency for the condensate in double-well trap potential.
Vortex lattice in double-well
potential
Visible vortices=36
Hidden vortices=22
Feynman rule
Vortices number even
since DW-potential is
even parity.
In order to see how the visible vortices distributes itself across the central barrier of the
double-well potential, we consider an asymmetric double-well potential, where the depth
of the well on the right is more than that at the left of the central barrier region
This type of asymmetric double-well is created experimentally (Hall et al, PRL. 2007)
Odd number of vortices
Right-well: 7 visible vortices forming Abrikosov lattice and 5 hidden vortices.
Left-well: 3 visible vortices and 9 hidden vortices.
Vortices in triple-well trap potential
In the central-well, there is a linear chain of vortices, whereas in the neighboring two
wells the vortices forms the usual Abrikosov lattice structure. The linear vortex array is
useful for applications.
The hidden vortices that forms in the two barrier regions is shown in the phase profile.
The rule
is satisfied in this case also.
Feynman Rule: It is a relation between the number of vortices and the angular frequency
of rotation. Feynman showed that for a superfluid rotating in a rigid container of radius R,
the number of vortices are given by
For harmonically trapped rotating BEC, this relation is modified as (Fetter, RMP 2009)
where the radius of the rotating condensate is given by
This relation shows that the radius and hence the number of vortices diverges
when the frequency of the rotation approaches the harmonic trap frequency, i.e. in
the dimensionless unit,
However, no such divergence have been observed in the recent experiment (Williams et al,
PRL 2010).
To explain this, recently Kato et al (PRA 2011) argued that such divergence in the number
of vortices can be avoided if one considers an optical lattice with Gaussian envelope.
We on the other hand show that the divergence can be avoided if the double-well trap
potential is anisotropic.
For this we calculate the Feynman rule for the number of vortices in the rotating condensate
trapped in a anisotropic double-well potential using Thomas Fermi approximation as
For
the rotation at
For harmonic trap b=0 and
is also possible, in agreement with the experiment.
, then
and we get back the previous result for the harmonic trap
PINNING OF VISIBLE AND HIDDEN VORTICES IN OPTICAL LATTICE
Optical lattice : an artificial crystal of light – a periodic intensity pattern that
is formed by the interference of two or more laser beams. More lasers give
3D spatial structure.
Trapping atom in optical lattice – atoms can be trapped in the bright or dark
regions of the optical lattice via Stark shift.
Strength of the optical potential confining can be increased by increasing
laser intensity.
BEC mounted on a optical lattice is like electrons in a periodic potential of
ions in conventional solid. Condensate atoms plays the role of electrons
and optical lattice the role of ions.
We have considered the optical lattices as
The dynamics of condensate in a pancake-shaped rotating trap and co-rotating optical lattice
is described by GPE equation
Where V(x,y) is the sum of the trap potential and optical lattice potential.
Force acting on a vortex = driving force + pinning force + force from other vortices
Driving force = Magnus force + mutual friction force (arising due to interaction between
vortex core and the normal fluid flow).
Pinning force = The vortices gets pinned at the maximum of the lattice potential.
This can be seen by calculating the potential energy of a vortex in the condensate in
optical lattice. Reijinders and Duine, PRL 2004.
For this consider variational ansatz for the condensate wavefunction as
where phase
Substituting in
We get interaction energy as
where
which has minimum when vortices are at maximum of the optical lattice.
Fig: For the strength of the optical lattice
the Abrikosov vortex lattice is completely
pinned to the triangular optical lattice (Fig. (a)) but partially pinned to the square optical
lattice (Fig. (B)). But for higher strength
Abrikosov vortex lattice is completely pinned
To the square optical lattice (Fig. ( c )).
For further increase of the strength of the square optical lattice
, we find that
there is a “defect vortex” in both the wells. (Fig. (d)). This type of defect vortices has been
observed in experiment ( Tung et al, PRL 2006)). All other vortices are pinned.
As expected, such defect vortices are not seen in triangular optical lattice (Fig. (e)).
Pinning of vortices in rotating BEC trapped in triple-well potential and co-rotating optical
lattice.
Fig. : Pinned vortex lattice for (a) triangular optical lattice – alternate vortices pinned in
central well. In the neighbouring well all Abrikosov vortices are pinned
and (b) square optical lattice – all vortices pinned in the central well. In the neighbouring
well all vortices are pinned except the defect vortices.
Pinning of hidden vortices – Difficult problem. Since pinning if any, can be seen only
in the phase profile of the condensate density.
To see pinning of hidden vortices clearly, we first increase the number of hidden vortices
-This can be done by increasing the width of the central barrier region so that it can
accommodate more number of hidden vortices.
We find that a new type of hidden vortices appear whose phase profile is similar to
that of the visible vortices. These new type of hidden vortices are shown by
red dots.
Interestingly, we find that only this new type of hidden vortices can be pinned to the optical
lattice. Shown by red dots in the phase profile of the condensate. However, for pinning of the
hidden vortices, the strength of the optical lattice should be much stronger.
Variation of lattice potential energy with strength of the optical lattice to examine
vortex lattice transition.
Triangular optical lattice
Square optical lattice