* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Higher Physics – Unit 2
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Centripetal force wikipedia , lookup
N-body problem wikipedia , lookup
Atomic theory wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Work (physics) wikipedia , lookup
Seismometer wikipedia , lookup
Equivalence principle wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Center of mass wikipedia , lookup
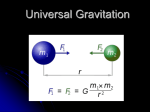
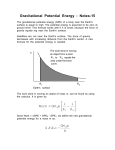
Advanced Higher Physics Unit 1 Gravitation Gravitation investigation Planet Mercury Venus Earth Mars Jupiter Saturn Uranus Neptune m (kg) T (s) r, distance w from sun (m) (radsˉ¹) Fc (N) m/r² Planet mass (x10^24 kg) T(s) w F r (x10^9 m) m/r² mercury 0.33 7600176 8.26716E-07 1.30589E+22 57.9 9.84366E-23 venus 4.87 19394640 3.23965E-07 5.53035E+22 108.2 4.15982E-22 earth 5.98 31536000 1.99238E-07 3.55123E+22 149.6 2.67201E-22 mars 0.65 59319216 1.05922E-07 1.03263E+21 141.6 3.2418E-23 jupiter 1900 3.74E+08 1.6785E-08 4.16625E+23 778.3 3.1366E-21 saturn 570 9.29E+08 6.76531E-09 3.72284E+22 1427 2.79915E-22 uranus 57 2.65E+09 2.36991E-09 9.19121E+20 2871 6.91526E-24 neptune 100 5.2E+09 1.20824E-09 6.56505E+20 4497.1 4.94464E-24 Relationship between Fg and r Plot a graph of Fg against m/r². Fg (N) m/r²(kgmˉ²) Fg(N) Fg against m/d^2 4.5E+23 4E+23 3.5E+23 3E+23 2.5E+23 2E+23 1.5E+23 1E+23 5E+22 0 0 1E-21 2E-21 m /d^2 (kgm ^-2) 3E-21 4E-21 Inverse square law of gravitation The Force of gravitational attraction between any two particles is given by: Gm1m2 F 2 r F is the gravitational force, measured in Newton (N) G is the universal constant of gravitation, G 6.67 1011 Nm2 kg 2 On data sheet m1 and m2 are the masses of the particles in kg r is the distance between the two particles in m Notes: •For orbits, r is taken as the centre of orbit which are taken as circular. In reality, they are not circular. •The mass of a large body can be considered to be concentrated at its centre. Find the mass of the sun Find the gradient of the graph Fg against m/r². m1 Fg k 2 r Gm1m2 F 2 r However, Therefore k Gm2 So mass of the sun = with k m2 G m2= mass of the sun G=universal constant of gravitation Example A spacecraft is travelling from the Earth to the moon. Calculate the distance from the spacecraft to the earth when the resultant gravitational force acting on the spacecraft is 0. (Mean radius of the moon’s orbit is 3.8 108 m ) Fmoon Fearth Gravitational Field Strength The gravitational field strength reduces with increasing distance. The gravitational field strength at a point is defined as the force acting on a 1kg mass at that point. F g m Not in data booklet Now we have two expressions for gravitational force: F mg and If mass of object = m=m2, Gm1m2 F 2 r Equating these and cancelling the mass of the object gives Gm1 g 2 r With m1, mass of the Earth. Not in data booklet. Weighing the Earth Calculate the mass of the earth using Gm2 g 2 r Gravitational Fields A gravitational field line shows the direction of the force a small test mass would experience if placed at that point. Isolated point mass Two equal point masses Gravitational Potential The gravitational potential a point is the work done to move 1 kg Mass from infinity to that point. Using calculus: V is measured in Jkgˉ¹ V=0 at infinity Work V mass Not in data booklet Gm V r In data booklet m mass of the planet, kg r distance from centre of planet m At this point, the potential is: Gm V r r m The work done in bringing the satellite to this point is: r Gm V r m The potential is negative as it becomes less when the satellite gets closer or more when it gets further away. Potential energy The potential energy of a mass M at a point is: E p MV Not in data booklet Therefore: GMm Ep r m, mass of the planet in kg M, mass of the object in kg r, distance from centre of planet to object in m M The potential energy of the satellite is: r GMm Ep r m A gravitational field is a conservative field. The potential energy of an object depends on its position and not how it was placed in that position. Also the overall energy required to move a mass on a round trip is 0. Example A 800 kg satellite is to be placed in a circular orbit 1200 km above the surface of the Earth. 1. Calculate the gravitational potential of the satellite. 2. Calculate its gravitational potential energy. 3. How does the gravitational energy of the satellite compare with its gravitational energy on the Earth’s surface. Escape velocity Consider a mass m2, at the surface of a large body of mass m1 and radius r. m2 To escape the gravitational field of the large body, the mass must be given enough kinetic energy so that when it reaches “infinity” its kinetic energy is 0. r In other words, enough kinetic energy to overcome the potential energy at the surface. m1 At all points: Ek E p 0 1 2 GMm mv 0 2 r 2GM v r 2 You need to be able to derive this ! In data booklet 2GM v r Black holes and photons If the gravitational field of a body is sufficiently large, photons will be affected by it. In some cases the escape velocity for a body is larger than c, and so nothing can escape its surface, not even light. Such a body is called a black hole. Example Calculate the radius of the earth for it to become a black hole. Satellites in circular motion To maintain a circular motion, there must be a centripetal force. The only force which can do this is the gravitational force. v m2 r F m1 2 m2v Gm1m2 2 r r m2v 2 Gm1m2 r r2 Gm1 v r 2 m1 is the mass of the large object (example Earth) Measuring the mass of the milky way The sun orbits the galactic center at: r 2.6 10 m 20 v 2.2 10 ms 5 Use 1 Gm1 v r 2 to find the mass of the milky way. GM v r 2 Now substitute 2r v T 4 2 r 2 GM 2 T r2 3 4 r 2 T GM r3 T 2 GM Now consider energy: GM v r 2 , so 1 2 GMm mv 2 2r GMm Ek 2r We already have an expression for potential energy: GMm Ep r Therefore the total energy of the system is: GMm Ek E p 2r