Download Chapters 6 and 8: Some Additional Forces

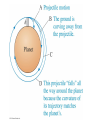
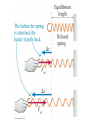
Chapters 6 and 8: Some Additional
Forces
• Key Terms
– Newton’s Law of Gravity
– Orbit
– Hooke’s Law
– Equilibrium position
Orbital Motion
• If a launch speed is great enough, there comes
a point at which the curve of the trajectory
and the curve of the earth are parallel.
• In this case, the projectile “falls” but it never
gets any closer to the ground!
• Such a trajectory around a planet or star is
called an “orbit”.
Weightlessness in Orbit
• Weightlessness does not occur from an absence
of weight or gravity.
• Instead, astronauts in orbit are “weightless”
(apparent weight of 0) because they are falling
freely, along with the spacecraft and everything
in it.
• Space stations rotate to create “artificial gravity”
for safety.
Newton’s Law of Gravity
• The force that attracts the moon to the earth
(and the planets to the sun) is identical to the
force that attracts an apple to the earth.
Sample Problem #1 (Ex. 6.14, page
186)
• The gravitational force between two giant lead
spheres is 0.010 N when the centers of the
spheres are 20 m apart. What is the distance
between their centers when the gravitational
force is 0.160 N?
Sample Problem #2 (Ex. 6.15, page
187)
• You are seated in your physics class next to
another student 0.60 m away. Determine the
magnitude of the gravitational force between
you assuming that you both have a mass of 65
kg.
Sample Problem #3 (Ex. 6.16, page
187)
• What is the magnitude of the gravitational
force of the earth on a 60 kg person? The
earth has a mass of 5.98 x 1024 kg and radius
6.37 x 106 m.
Sample Problem #4 (Ex. 6.17, page
189)
• Saturn, at 5.68 x 1026 kg, has nearly 100 times
the mass of the earth. It is also much larger,
with a radius of 5.85 x 107 m. What is the
value of g on the surface of Saturn?
Sample Problem #5 (Ex. 6.18, page
189)
• Mars has two moons, each much smaller than
the earth’s moon. The smaller of these two
bodies, Deimos, has an average radius of 6.3
kmand a mass of 1.8 x 1015 kg. At what speed
would a projectile movie in a very low orbit
around Deimos?
• How much time would it take to complete this
orbit?
Elastic Systems
• A system that exhibits a restoring force is
called elastic.
• Examples: rubber bands, springs
• When no forces act on a spring to compress or
extend it, it will relax to its equilibrium
position.
Hooke’s Law
• The negative sign reflects the fact that the
force due to a spring always opposes to
direction of stretching/compression.
Sample Problem #6 (Ex. 8.6, page 240)
• A scale used to weight a fish consists of a
spring connected to the ceiling. The spring’s
equilibrium length is 30 cm. When a 4.0 kg
fish is suspended from the end of the spring, it
stretches to a length of 42 cm.
– A) What is the spring constant for this spring?
– B) If an 8.0 kg fish is suspended from the spring,
what will be the length of the spring?
Sample Problem #7 (Ex. 8.7, page 241)
• The figure below shows a spring attached to a 2.0 kg block.
The other end of the spring is pulled by a motorized toy train
that moves forward at 5.0 cm/s. The spring constant is 50
N/m, and the coefficient of static friction between the block
and the surface is 0.60. The spring is at its equilibrium length
at t = 0 s, when the train starts to move. When does the block
slip?