Download Document

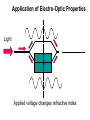
• Linear optical properties of
dielectrics
• Introduction to crystal optics
• Introduction to nonlinear optics
• Relationship between nonlinear
optics and electro-optics
Bernard Kippelen
Maxwell's Equations and the Constitutive
Equations
Light beams are represented by electromagnetic waves propagating in
space. An electromagnetic wave is described by two vector fields: the
electric field E(r, t) and the magnetic field H(r, t).
In free space (i.e. in vacuum or air) they satisfy a set of coupled
partial differential equations known as Maxwell's equations.




E
 H  0
t
H
 E   0
t
 E 0
MKS
 H 0
0 and 0 are called the free
space electric permittivity and
the free space magnetic
permeability, respectively, and
satisfy the condition
c2 = (1 / (0 0)), where c is the
speed of light.
In a dielectric medium: two more field
vectors
D(r,t) the electric displacement field, and B(r,t) the magnetic
induction field
D
  H 
 j
t
  E 
  D
  B0
B
t
Constitutive equations:
D  0 E  P   E
B  0 H
 is the electric permittivity (also called
MKS
 and j are the electric charge density
(density of free conduction carriers) and
the current density vector in the medium,
respectively. For a transparent dielectric
 and j =0.
dielectric function) and P = P (r, t) is the
polarization vector of the medium.
Linear, Nondispersive, Homogeneous, and
Isotropic Dielectric Media
Linear: the vector field P(r, t) is linearly related to the vector field E(r, t).
Nondispersive: its response is instantaneous, meaning that the
polarization at time t depends only on the electric field at that same
time t and not by prior values of E
Homogeneous: the response of the material to an electric field is
independent of r.
Isotropic: if the relation between E and P is
independent of the direction of the field vector E.
P (r ,t )   0  E (r ,t ) (MKS)
P (r ,t )   E (r ,t ) (CGS)
   0 (1   ) (MKS)
 = 1 + 4   (CGS)
 is called the optical susceptibility
Wave equation
From Maxwell’s equations and
by using the identity:   (  E )  (  E )   2 E
n  E
 E 2
0
2
c t
2
2
2
n  1  

 r
0
n  1  4  
(MKS)
(CGS)
Solutions of Wave Equation
E (r ,t ) =  cos (kr   t)  Re  ei(kr   t)  
1
 ei(kr   t)  c .c .  E ei(kr   t)  c .c .

2
Real
number
Complex Complex
number conjugate
Period T = 2/
Dispersion
relationship
Time
Wavelength  = 2/k
Space

n
k 
v
c
In real materials: polarization induced by an
electric field is not instantaneous
t
P(t) 
  (t   ) E(  )d 

Which can be rewritten in
the frequency domain
P(  )   (  ) E(  )
• the susceptibility is a complex number: has a
real and imaginary part (absorption)
• the optical properties are frequency dependent
Lorentz oscillator model
Electron
Absorption
Refractive Index

Photon Energy
Nucleus
Displacement
around
equilibrium
position due to
Coulomb force
exerted by
electric field
Optics of Anisotropic Media
Optical properties (refractive index depend on the orientation of electric
field vector E with respect to optical axis of material
Z
Y
X
Need to define tensors to describe
relationships between field vectors
PX  11 E X  12 EY  13 EZ
PY   21 E X   22 EY   23 EZ
PZ   31 E X   32 EY   33 EZ
 11
    21

 31
12
 22
 32
13 
 23 
 33 
 Pi    ij E j
j
Uniaxial crystals – Index ellipsoid
2
0   nX
  11 0



   0  22 0    0

 0
0  33   0


nX = nY ordinary index
nZ = extraordinary index
Refractive index for arbitrary
direction of propagation can be
derived from the index ellipsoid
1
cos 2  sin 2 


2
2
n ( )
no
ne2
0
nY2
0
0 

0 

nZ2 
Introduction to Nonlinear Optics
P(E)   L E   ( 2 ) E E   ( 3 ) EEE  ...
Linear term
Nonlinear corrections
Example of second-order effect: second
harmonic generation (Franken 1961):
Symmetry restriction for second-order processes
Several electric fields are present
E( r ,t)   E( n )e  i n t  c .c
n
P ( r ,t)   P (  n )e  i n t  c .c
n
Nonlinear polarization
(2)
P(



)

D

 ijk ( n  m ;n ,m ) E j ( n ) Ek ( m )
i
n
m
jk
Tensorial relationship between field and polarization
2)
 PX( 2 )    (XXX
 (2)   (2)
 PY    YXX
 (2)   (2)
 PZ    ZXX

 
2)
 (XYY
2)
 (XZZ
2)
 (XYZ
2)
 (XXZ
2) 
 (XXY
(2)
YYY
(2)
 ZYY
(2)
YZZ
(2)
 ZZZ
(2)
YYZ
(2)
 ZYZ
(2)
YXZ
(2)
 ZXZ
(2)
YXY
(2)
 ZXY





 E X2 


2
 EY 


2
E


Z
 2E E 
 Y Z
 2 E X EZ 
2E E 
 X Y
Second-order nonlinear
susceptibility tensor
~ ( 2)
( 2)
  11

( 2)
   21
 ( 2)
  31
( 2)
 12
( 2)
 22
( 2)
 32
( 2)
 13
( 2)
 23
( 2)
 33
( 2)
 14
( 2)
 24
( 2)
 34
( 2)
 15
( 2)
 25
( 2)
 35
( 2) 
 16

( 2)
 26 
( 2) 

 36

Contracted notation for last two indices: xx = 1; yy = 2, zz = 3; zy or yz = 4;
zx or xz = 5; xy or yx = 6
18 independent tensor elements but can be reduced by invoking group theory
(2)
 0
0
0
0
15
0


(2)
(2)

 0
0
0
15
0
0
 (2)

(2)
(2)
  31



0
0
0
31
33


Example: tensor for poled electro-optic polymers
Introduction to Electro-optics
John Kerr and Friedrich Pockels discovered in 1875 and 1893, respectively,
that the refractive index of a material could be changed by applying a dc or low
frequency electric field
n(E0 )  n( E0  0 ) 
1 3
1 3 2
n r E0 
n s E0  ...
2
2
In this formalism, the effect of the applied electric field was to deform
the index ellipsoid
 1  2
 1  2
 2 X   2 Y 
 n 1
 n 2
 1 
 1 
2  2  XZ  2  2  XY
 n 5
 n 6
 1  2
 1 
 2  Z  2  2  YZ 
 n 3
 n 4
1
Index ellipsoid equation
 1 
 2  
 n i
3
 rij
j 1
Corrections to the
coefficients
E0 j
Electro-optic tensor
  1  
  2  
  n 1 
  1  
 2  
  n  2   r11
  1    r21
 2   
  n 3   r31

  r
1
      41
  n 2 4   r51

  r
1



  61


2
  n 5 


1




  n 2  
6

Relationship with second-order
susceptibility tensor:
r12
r22
r32
r42
r52
r62
r13 
r23 
r33 

r43 
r53 

r63 
 E0 X
E
 0Y
E
 0Z





Simplification of the tensor due to
group theory
rij  
8
n4
 (ji2 )
Example of tensor for electrooptic polymers
0

0
0
r 
0
r
 13
0
0
0
0
r13
0
0
r13 

r13 
r33 

0 
0 

0 
Application of Electro-Optic Properties
Light
Applied voltage changes refractive index
Electro-Optic Properties of Organics
hyperpolarizabilities
p E  E  E
2
A
3
D
nonlinear susceptibilities

P   (1) E   ( 2 ) E 2   (3) E 3 ...
If the molecules are randomly
oriented
inversion symmetry
(2)

0
The Photorefractive Effect
a
T ran sp o rt
Convert an intensity distribution
into a refractive index distribution
b
T ra p p in g
c
d
e

D e p h a s in g
S pace