Download Chapter 5 Section 5.1 * Midsegments of Triangles

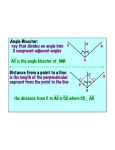
Chapter 5
Section 5.1 – Midsegments
of Triangles
Objectives:
To use properties of midsegments to
solve problems
C
L
A
N
B
In triangle ABC above, LN is a triangle midsegment.
Midsegment - > of a triangle is a segment connecting
the midpoints of two sides.
Theorem 5.1 -> Triangle Midsegment Theorem
If a segment joins the midpoints of two sides of
a triangle, then the segment is parallel to the third
side, and is half its length
LN II AB
-and-
1
LN =
2
AB
Ex: Finding the Length of Segments
In triangle EFG, H, J, and K are midpoints. Find HJ, JK,
and FG.
F
60
H
J
40
E
K
100
G
Ex:
AB = 10 and CD = 18. Find EB, BC, and AC.
A
E
D
B
C
Ex: Identifying Parallel Segments
In triangle DEF, A, B, and C are midpoints.
Name three pairs of parallel segments.
E
B
A
D
C
F
Find the measure of <VUZ. Justify your
answer.
X
65
U
Y
V
Z
Homework #26
Due Friday (November 16)
Page 262 – 263
#1 – 19 odd
#22 – 25 all
Section 5.2 – Bisectors in Triangles
Objectives:
To use properties of perpendicular
bisectors and angle bisectors
In the diagram below to the left, CD is the
perpendicular bisector of AB. CD is perpendicular
to AB at its midpoint. The diagram below to the
right, CA and CB are drawn to complete the
triangles CAD and CBD.
C
C
A
D
B
A
D
B
Theorem 5.2 – Perpendicular Bisector Theorem
If a point is on the perpendicular bisector of a
segment, then it is equidistant from the endpoints of
the segment.
Theorem 5.3 – Converse of the Perpendicular
Bisector Theorem
If a point is equidistant from the endpoints of a
segment, then it is on the perpendicular bisector of
the segment.
Example:
CD is the perpendicular bisector of AB. Find
CA and DB. Explain your reasoning.
C
5
A
B
6
D
Distance from a point to a line -> the length of the
perpendicular segment from the point to the line. In
the diagram below, AD is the bisector of <CAB. If you
measure the lengths of the perpendicular segments
from D to the two sides of the angle, you will find that
the lengths are equal. Therefore, D is equidistant from
the sides.
C
A
D
B
Theorem 5.4 – Angle Bisector Theorem
If a point is on the bisector of an angle, then the
point is equidistant from the sides of the angle.
Theorem 5.5 – Converse of the Angle Bisector
Theorem
If a point in the interior of an angle is
equidistant from the sides of the angle, then the point
is on the angle bisector.
Ex: Using the Angle Bisector Theorem
What is the length of FD ?
C
D
B
2x + 24
5x
A
F
E
A.According to the diagram, how far is K
from EH? From ED?
B.What can you conclude about EK?
C.Find the value of x.
D.Find m<DEH
D
2x
K
E
10
x + 20
H
Homework # 27
Due Friday (November 16)
Page 267 – 268
#1 – 31 odd
Section 5.3 – Concurrent Lines,
Medians, and Altitudes
Objectives: To identify properties of perpendicular
bisectors and angle bisectors.
To identify properties of medians and
altitudes of a triangle.
Concurrent -> when three or more lines intersect in
one point.
Point of Concurrency -> the point at which three or
more lines intersect.
Theorem 5.6
The perpendicular bisectors of the sides of
a triangle are concurrent at a point equidistant
from the vertices.
Theorem 5.7
The bisectors of the angles of a triangle are
concurrent at a point equidistant from the sides.
Circumcenter of the Triangle -> the point of concurrency
of the perpendicular bisectors of a triangle. In triangle
QRS (below), points Q, R, and S are equidistant from C,
the circumcenter. The circle is circumscribed about the
triangle
S
C
Q
R
Ex: Finding the Circumcenter
Find the center of the circle that you can
circumscribe about a triangle with vertices (0,0),
(4,0), and (0,6).
Find the center of the circle that you can
circumscribe about the triangle with vertices (0,0),
(-8,0), and (0,6).
Why is it not necessary to find the third
perpendicular bisector?
The figure below shows triangle UTV with the bisectors of
its angles concurrent at J. The point of concurrency of the
angle bisectors of a triangle is called the incenter of the
triangle.
Points X, Y, Z are equidistant from J, the incenter, The
circle is inscribed in the triangle.
T
Y
X
U
XJ = YJ = ZJ
J
V
Z
Median of a Triangle -> a segment whose endpoints
are a vertex and the midpoint of the opposite side.
Theorem 5.8 – Triangle Medians Theorem
The medians of a triangle are concurrent at a
point that is two thirds the distance from each vertex
to the midpoint of the opposite side.
D
2
DC = DJ
3
H
C
E
G
J
F
2
FC = FH
3
2
EC = EG
3
Centroid -> the point of concurrency of the medians in
a triangle.
**Also called the center of gravity of a triangle
because is the point where a triangular shape
will balance.**
Example: Finding Lengths in Medians
In triangle ABC below, D is the centroid and DE
= 6. Find BE. Find BD.
B
D
A
E
C
Altitude of a Triangle -> the perpendicular segment
from a vertex to the line containing the opposite side.
**Unlike angle bisectors and medians, an
altitude of a triangle can be a side of a triangle
or it may lie outside the triangle.**
Acute Triangle
Altitude is inside
Right Triangle
Altitude is a side
Obtuse Triangle
Altitude is outside
Theorem 5.9
The lines that contain the altitudes of a triangle
are concurrent.
Orthocenter of the Triangle -> the point at which the
lines containing the altitudes of a triangle are
concurrent
Homework #28
Due Monday (November 26)
Page 275 – 276
# 1 – 22 all
Section 5.4 – Inverses, Contrapositives,
and Indirect Reasoning
Objectives:
To write the negation of a statement and the
inverse and contrapositive of a conditional
statement
To use indirect reasoning
Negation -> of a statement has the opposite
truth value.
Ex: Los Angeles is the capital of California
(false)
Los Angeles is not the capital of California
(true)
Inverse -> negates both the hypothesis and the
conclusion of a conditional statement.
Contrapositive -> switches the hypothesis and the
conclusion of a conditional statement and
negates both.
Equivalent Statements -> statements that have
exactly the same truth value.
Summary -> Negation, Inverse, and
Contrapositive Statements
Statement
Example
Symbolic Form
You Read It
Conditional
If an angle is a straight
angle, then its measure
is 180
p -> q
If p, then q.
Negation (of p)
An angle is not a
straight angle.
~p
Not p.
Inverse
If an angles is not a
straight angle, then its
measure is not 180.
~p -> ~q
If not p, then not q.
Contrapositive
If an angle’s measure is
not 180, then it is not a
straight angle.
~q -> ~p
If not q, then not p.
Examples:
Write the negation of each statement.
<ABC is obtuse.
m <JKL is > 70.
Lines m and n are not perpendicular.
Today is not Tuesday.
Write the inverse and the contrapositive of the
conditional statement.
If a figure is a square, then it is a rectangle.
If you don’t stand for something, you’ll fall for anything.
Suppose your brother tells you, “Your girlfriend called a
few minutes ago.” You think through these three steps:
Step 1 – You have two girlfriends.
Step 2 – You know that one of them is at cheerleading
practice.
Step 3 – You conclude that the other one must have
been the one that called.
This type of reasoning is called indirect reasoning.
In this type of reasoning, all possibilities are considered
and then all but one are proved false. Ergo, the
remaining possibility must be true. A proof involving
indirect reasoning is an indirect proof.
Summary -> Writing an Indirect Proof
Step 1 – State as an assumption the
opposite (negation) of what you want to
prove.
Step 2 – Show that this assumption leads
to a contradiction.
Step 3 – Conclude that the assumption
must be false and that what you want to
prove must be true.
Homework # 29
Due Tuesday (November 27)
Page 283
#1 – 19 all
Section 5.5 – Inequalities in Triangles
Objectives: To use inequalities involving angles of triangles
To use inequalities involving sides of triangles
Comparison Property of Inequality
If a = b + c and c > 0, then a > b
Corollary to the Triangle Exterior Angle Theorem
The measure of an exterior angle of a triangle is
greater than the measure of each of its remote interior
angles.
3
m<1 greater than m<2
m<1 greater than m<3
2
1
Theorem 5.10
If two sides of a triangle are not congruent,
then the larger angle lies opposite the longer
side.
Y
If XZ > XY, then m<Y
greater than m<Z
X
Z
Ex:
List the angles of triangle ABC in order from
smallest to largest.
A
C
B
Theorem 5.11 (Converse of 5.10)
If two angles of a triangle are not congruent,
then the longer side lies opposite the larger angle.
B
If m<A greater than
m<B, then BC > AC
C
A
Ex:
List the sides in order from shortest to longest.
T
U
58
62
V
Theorem 5.12 – Triangle Inequality Theorem
The sum of the lengths of any two sides of a
triangle is greater than the length of the third side.
Y
XY + YZ > XZ
YZ + ZX > YX
ZX + XY > ZY
X
Z
Ex:
Can a triangle have sides with the given lengths?
Explain.
a. 3ft, 7ft, 8ft
b. 3cm, 6cm, 10cm
A triangle has sides of lengths 8cm and 10 cm. Describe
the lengths possible for the third side.
Homework #30
Due Wednesday (Nov 28)
Page 292 – 293
# 1 – 27 all
Chapter 5 Test Thursday/Friday