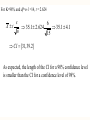* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Confidence Interval
Survey
Document related concepts
Transcript
o Make Copies of: o Areas under the Normal Curve o Appendix B.1, page 784 o (Student’s t distribution) o Appendix B.2, page 785 o Binomial Probability Distribution o Appendix B.9, pages 794,798 n x p( x) P( X x) p (1 p) n x x Confidence Interval Definition: A range of values constructed from sample data so that the population parameter is likely to occur within that range at a specified probability. The specified probability is called the level of confidence. Ex. We are 90% sure that the mean yearly income of construction workers in the New York area is between $61,000 and $69,000. Confidence Interval If normal and σ known The CI is given by: [X z n ,X z n ] X , σ and n are known. We can obtain z from Appendix B.1 by looking for a value of z that satisfies: (Area from 0 to z) = K/2 = (level of confidence)/2 Confidence Interval If (normal, σ unknown and n>30) or If (not normal and n>30) The CI is given by: s s [X z ,X z ] n n X , σ and n are known. We can obtain z from Appendix B.1 by looking for a value of z that satisfies: (Area from 0 to z) = K/2 = (level of confidence)/2 Confidence Interval If (normal, σ unknown and n≤30) The CI is given by: s s [X t , X t ] n n X , σ and n are known. We can obtain t from Appendix B.2 by looking for a value of t that satisfies the level of confidence (K%) and the degrees of freedom (df=n-1). Confidence Interval, c df = n-1 . 9 10 90% 95% 98% 99% When to Use the t Distribution Is the population normal? No Yes Is the population SD known? Is n 30 or more? No Use a nonparametric test Yes Use the z distribution No Use the t distribution Yes Use the z distribution When to Use the t Distribution Is the population normal? No Yes Is the population SD known? Is n 30 or more? No Use a nonparametric test Yes Use the z distribution No Use t if n less than or equal to 30, Use z if n is more than 30 Yes Use the z distribution Example(ex14, page309): Develop a 90% CI interval for the population mean. Develop a 98% CI for the population mean. Interpret the result. 29,38,38,33,38,21,45,34,40,37,37,42,30,29,35 o o o o o n=15 < 30 Assume Normal distribution otherwise we can not use the t distribution. Sample Mean = 35.1, Sample SD = 6.0 For K=90% and df=n-1 =14, t = 1.761 s X t n 6 35.1 1.761 35.1 2.7 15 CI [32.4,37.8] For K=98% and df=n-1 =14, t = 2.624 s 6 X t 35.1 2.624 35.1 4.1 n 15 CI [31,39.2] As expected, the length of the CI for a 90% confidence level is smaller than the CI for a confidence level of 98%. Confidence Interval When looking for a value for z in the expression, X z n 95% of the sample means selected from a population will be within 1.96 SD’s of the population mean µ. (The z value for a confidence level of 95% is 1.96). 99% of the sample means will lie within 2.58 SD’s of the population mean. (The z value for a confidence level of 99% is 2.58). Confidence Interval How did we get the 1.96 and the 2.58 for the 95% and 99% confidence intervals? For the 95% CI: Probability area is 0.95/2=0.475. In Appendix B.1, the z value for .475 is 1.96. Use same reasoning and calculations for the 99% CI. Probability area is 0.99/2=0.495. In Appendix B.1, the z value for .495is 2.58. Finite-Population Correction Factor If the population size N is not very large, then we use a population correction factor when computing the CI. If (n/N > 0.05) then use : s X t n N n N 1 N n N 1 X z n , OR s X z n N n N 1 Example: There are 250 families in a certain area. A poll of 40 families reveals the mean spending per week is $450 with a standard deviation of $75. Construct a 90% CI for the mean spending. n/N = 40/250 = 0.16 > 0.05. s X z n N n 75 450 1.65 N 1 40 450 17.97 250 40 250 1 Finite-Population Correction Factor A population that has a fixed upper bound limit. A small population. Ex. Students registered for this class. When population is finite, need to make adjustments in the way we compute the standard error of the sample means, and the standard error of the sample proportion. Reduce the Standard Error The adjustment is called the finite-population correction factor. Sample Size Fraction of population (size 1000) Correction Factor 10 .01 .9955 50 .05 .9752 100 .1 .9492 500 .5 .7075 Sample Size for Estimating Population Mean zs n E 2 n is the sample size; z is the standard normal value corresponding to the desired level of confidence; s is an estimate of the population SD; E is the maximum allowable error (1/2 length of the CI). If the result is not a whole number, round up. Example: A student wants to determine the mean amount of earnings per month of city council members. The error in estimating the mean is to be less than $100 with a 95% level of confidence. The student found a report by the Department of Labor that estimated the SD to be $1,000. What is the required sample size? K=95% => z=1.96 Error in the estimating mean is to be less than 100 =>E=100 SD=1000 2 2 zs (1.96)(1000) n 384.16 100 E Round up => sample size n = 385 What if the student wanted to increase the level of confidence to 99%? The corresponding z value for k=99% is 2.58. 2 2 zs (2.58)($ 1,000) 2 n ( 25 . 8 ) 665.64 $100 E The recommended sample size is now 666. Notice the change in the required sample size for the different levels of confidence. There is an increase of 281 observations. This could greatly increase the cost and the time of the study. Therefore, the level of confidence should be considered carefully. Sample Size for Estimating Population Mean zs n E 2 o Sample size increase if we need a smaller CI (more precision). o Sample size increases if we need a higher Confidence Level (as K% increase then z increases and as a result, n increases). o If the SD increases (higher variability), then the sample size increases. Proportion o So far the populations characteristics we considered have numerical values. o If the population characteristic we are looking for can only take on two values (true or false), (yes or no), (1 or 0),… then we use a proportion to represent the population characteristic. o Proportion: The fraction, ratio, or percent indicating the part of the sample or the population having a particular trait of interest Proportion Example: A recent survey indicated that 92 out of 100 surveyed favored the continued use of daylight savings time in the summer. The sample proportion is 92/100, or .92, or 92%. o Define p as the sample proportion, and π as the population proportion. o p is the point estimate of π. o To estimate π, we can also construct a CI. Assumptions for Proportion CI Construction 1. 2. The binomial conditions have been met: a. Sample data is a result of counts. b. There are only 2 possible outcomes (Success and Failure). c. The probability of a success remains the same from one trial to the next. d. The trials are independent. The values nπ and n(1-π) should be both ≥5. (π is the population proportion) so that we can use the CLT (z-distribution) Sample Proportion X p n If π is the population proportion, then p is a point estimator for π. X is the number of (successes) obtained from the sample. Confidence Interval for a Population Proportion p z p Standard Error of the Sample Proportion p p(1 p) n Confidence Interval for a Population Proportion p(1 p) pz n Example: The union representing ABC company is considering a merger with Teamsters Union. According to ABC union bylaws, at least three-fourth of the union membership must approve any merger. A random sample of 2,000 current ABC members reveal 1,600 plan to vote for the merger proposal. What is the estimate of the population proportion? Develop a 95% confidence interval for the population proportion. Basing your decision on this sample information, can you conclude that the necessary proportion of ABC members favor the merger? Why? Sample size is N=2000, Number that approve the merger is X=1600. The sample proportion p=X/N=1600/2000 = 0.8. We determine the 95% CI. The z value is 1.96. p(1 p ) .80(1 .80) pz .80 1.96 .80 .018 n 2,000 Example (cont’d) The endpoints are .782 and .818. The lower limit is greater than .75. So, we conclude that the merger proposal will likely pass because the interval estimate includes values greater than 75% of the union membership. Sample Size for the Population Proportion Three items need to be specified: 1. The desired level of confidence. 2. The margin of error in the population proportion. 3. An estimate of the population proportion. z n p (1 p ) E 2 If an estimate of π is not available, use p=0.5 to approximately estimate the sample size. Example: A group of students want to estimate the proportion of cities with subsidized transportation systems. They want the estimate to be within .10 of the population proportion. The desired level of confidence is 90%. No estimate for the population proportion is available. What is the required sample size? E= .10 The level of confidence is 90%. The corresponding z value is 1.65. No estimate for p is available, so we use .50. 2 2 z 1.65 n p (1 p ) (.5)(1 .5) 68.0625 E .10 Round up, so a random sample of 69 cities is needed. Finite-Population Correction Factor If the population size N is not very large, then we use a population correction factor when computing the CI. If (n/N > 0.05) then use : p(1 p) N n pz n N 1 Example (ex22,page315): There are 300 welders at MSC. A sample of 30 welders revealed that 18 graduated from a registered welding course. Construct a 95% CI for the proportion of all welders who graduated from a registered welding course. p = X/n =18/30 = 0.6. n/N = 30/300=0.1>0.05 K=95% => z=1.96. pz p(1 p) N n n N 1 0.6(1 0.4) 300 30 0.6 1.96 30 300 1 CI 0.6 0.167 [0.433, 0.767]