Download Document

Linear Equations in Two
Variables
Linear Equations in Two Variables
may be put in the form
Ax + By = C,
Where A, B, and C are real
numbers and A and B are not
both zero.
Solutions to Linear Equations in Two
Variables

5 x  2 y  20
Consider the equation
 The equation’s solution set is
infinite because there are an
Ordered Pairs
infinite number of x’s and y’s
are listed with the
that make it TRUE.
x-value first and the y-value
second.
 For example, the ordered pair
(0, 10) is a solution because
 Can you list other ordered pairs
that satisfy this equation?
5 0  2 10  20
5 x  2 y  20
 
 
Input-Output Machines


We can think of equations as input-output machines. The
x-values being the “inputs” and the y-values being the
“outputs.”
Choosing any value for input and plugging it into the
equation, we solve for the output.
x=4
y = -2x + 5
y = -2(4) + 5
y = -8 + 5
y = -3
y = -3
Functions

Function- a relationship between two variables
(equation) so that for every INPUT there is
EXACTLY one OUTPUT.
 To determine (algebraically) if an equation is
a function we can examine its x/y table. If it is
possible to get two different outputs for a
certain input- it is NOT a function. In this
case an x-value in the table or ordered pairs
would repeat.
 This may be determined (graphically) by
using the Vertical Line Test. If any vertical
line would touch the graph at more than one
point- it is NOT a function.
Using Tables to List Solutions


For an equation
we can list some
solutions in a table.
Or, we may list the
solutions in ordered
pairs .
{(0,-4), (6,0), (3,-2),
( 3/2, -3), (-3,-6),
(-6,-8), … }
2 x  3 y  12
x
y
0
-4
6
0
3
-2
3/2
-3
-3
-6
-6
-8
…
…
Graphing a Solution Set
To obtain a more complete picture of a
solution set we can graph the ordered
pairs from our table onto a rectangular
coordinate system.
 Let’s familiarize ourselves with the
Cartesian coordinate system.

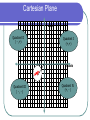
Cartesian Plane
y-axis
Quadrant II
( - ,+)
Quadrant I
(+,+)
x- axis
Quadrant III
(-,-)
Quadrant IV
(+, - )
Graphing Ordered Pairs on a Cartesian Plane
y-axis
1) Begin at the origin
2) Use the x-coordinate
to move right (+) or
left (-) on the x-axis
3) From that position
move either up(+) or
down(-) according to
the
y-coordinate
(6,0)
x- axis
4) Place a dot to indicate
a point on the plane
Examples: (0,-4)
(6, 0)
(-3,-6)
(0,-4)
(-3, -6)
Graphing More Ordered Pairs from our
Table for the equation
y
2 x  3 y  12
•Plotting more points
we see a pattern.
•Connecting the points
a line is formed.
x
(3,-2)
•We indicate that the
pattern continues by placing
arrows on the line.
•Every point on this line is a
solution of its equation.
(3/2,-3)
(-6, -8)
Graphing Linear Equations
in Two Variables





The graph of any linear
equation in two variables
is a straight line.
Finding intercepts can be
helpful when graphing.
The x-intercept is the
point where the line
crosses the x-axis.
The y-intercept is the
point where the line
crosses the y-axis.
On our previous graph,
y = 2x – 3y = 12, find the
intercepts.
y
x
Graphing Linear Equations
in Two Variables
y
On our previous graph,
y = 2x – 3y = 12, find
the intercepts.
The x-intercept is (6,0).
x
The y-intercept is (0,-4).
Finding INTERCEPTS

To find the
x-intercept: Plug in
ZERO for y and solve
for x.
2x – 3y = 12
2x – 3(0) = 12
2x = 12
x=6
Thus, the x-intercept is (6,0).
To find the
y-intercept: Plug in
ZERO for x and solve
for y.
2(0) – 3y = 12
2(0) – 3y = 12
-3y = 12
y = -4
Thus, the y-intercept is
(0,-4).
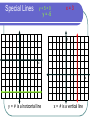
Special Lines
y+5=0
x=3
y = -5
y
y
x
x
y = # is a horizontal line
x = # is a vertical line
NCERT BOOK
QUESTIONS WITH THEIR SOLUTIONS
Exercise 4.1

Question 1:
The cost of a notebook is twice the cost of a pen. Write a linear
equation in two variables to represent this statement.
(Take the cost of a notebook to be Rs x and that of a pen to be
Rs y.)

Answer :
Let the cost of a notebook and a pen be x and y respectively.
Cost of notebook = 2 × Cost of pen
x = 2y
x − 2y = 0
Exercise 4.1

Question 2:
Express the following linear equations in the form ax + by + c = 0
and indicate the values of a, b, c in each case:
(i) 2x + 3y = 9.35

Answer :
(i) 2x + 3y = 9.35
2x + 3y – 9.35 = 0
Comparing this equation with ax + by + c = 0,
a = 2, b = 3, c = - 9.35
Exercise 4.2

Question 1:
Which one of the following options is true, and why?
y = 3x + 5 has
(i) a unique solution, (ii) only two solutions, (iii) infinitely many
solutions

Answer :
y = 3x + 5 is a linear equation in two variables and it has infinite
possible solutions. As for every value of x, there will be a value
of y satisfying the above equation and vice-versa.
Hence, the correct answer is (iii).
Exercise 4.2

Question 3:
Check which of the following are solutions of the equation x − 2y = 4 and
which are not:
(i) (0, 2 (ii) (2, 0)

Answer :
(i) (0, 2)
Putting x = 0 and y = 2 in the L.H.S of the given equation,
x − 2y = 0 − 2×2 = − 4 ≠ 4
L.H.S ≠ R.H.S
Therefore, (0, 2) is not a solution of this equation.
(ii) (2, 0)
Putting x = 2 and y = 0 in the L.H.S of the given equation,
x − 2y = 2 − 2 × 0 = 2 ≠ 4
L.H.S ≠ R.H.S
Therefore, (2, 0) is not a solution of this equation.
Exercise 4.2

Question 4:
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x +
3y = k.

Answer :
Putting x = 2 and y = 1 in the given equation,
2x + 3y = k
⇒ 2(2) + 3(1) = k
⇒4+3=k
⇒k=7
Therefore, the value of k is 7.
Exercise 4.3

Question 1:
Draw the graph of each of the following linear equations in two variable:
(i) y = 3x

Answer :
y = 3x
It can be observed that
x = −1, y = −3 and x = 1, y = 3
are solutions of the above equation.
Therefore, the solution table is as follows:
x
-1
1
y
-3
3
The graph of the above equation
is constructed as follows.
Exercise 4.3

Question 2:
Give the equations of two lines passing through (2, 14). How
many more such lines are there, and why?

Answer :
It can be observed that point (2, 14) satisfies the equation
7x − y = 0 and
x − y + 12 = 0.
Therefore, 7x − y = 0 and x − y + 12 = 0 are two lines
passing through point (2, 14).
As it is known that through one point, infinite number of lines
can pass through, therefore, there are infinite lines of such
type passing through the given point.
Exercise 4.3

Question 3:
If the point (3, 4) lies on the graph of the equation 3y = ax + 7,
find the value of a.

Answer :
Putting x = 3 and y = 4 in the given equation,
3y = ax + 7
3 (4) = a (3) + 7
5 = 3a
a=5/3
Exercise 4.3

Question 4:
The taxi fare in a city is as follows: For the first kilometre, the fares is Rs 8 and for the
subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as
Rs y, write a linear equation for this information, and draw its graph.
 Answer :
Total distance covered = x km
Fare for 1st kilometre = Rs 8
Fare for the rest of the distance = Rs (x − 1) 5
Total fare = Rs [8 + (x − 1) 5]
y = 8 + 5x − 5
y = 5x + 3
5x − y + 3 = 0
It can be observed that point (0, 3) and
(-3 / 5, 0) satisfies the above equation.
Therefore, these are the solutions of this equation.
x
0
-3/5
y
3
0
The graph of this equation is constructed as follows.
Here, it can be seen that variable x and y are representing the distance covered and the fare paid for
that distance respectively and these quantities may not be negative. Hence, only those values
of x andy which are lying in the 1st quadrant will be considered.
Exercise 4.3

Question 7:
Yamini and Fatima, two students of Class IX of a school, together
contributed Rs 100 towards the Prime Minister’s Relief Fund to help the
earthquake victims. Write a linear equation which satisfies this data. (You
may take their contributions as Rs x and Rs y.) Draw the graph of the
same.

Answer :
Let the amount that Yamini and Fatima contributed
be x and y respectively towards the Prime Minister’s Relief fund.
Amount contributed by Yamini + Amount contributed by Fatima = 100
x + y = 100
It can be observed that
(100, 0) and (0, 100) satisfy
the above equation. Therefore,
these are the solutions of the
above equation.
The graph is constructed as follows.
Exercise 4.4

Question 2:
Give the geometric representations of 2x + 9 = 0 as an equation
(1) in one variable
(2) in two variables

Answer :
(1) In one variable,
2x + 9 = 0 represents a point
x = - 9/2 = - 4.5 as shown
in the following figure.
(2) In two variables, 2x + 9 = 0
represents a straight line
passing through point
(−4.5, 0) and parallel to
y-axis. It is a collection of
all points of the plane, having
their x-coordinate as 4.5.
Let`s Practice
Something Interesting
Let`s Try To Do …..
Q1. Determine the point on the graph of the linear equation x + y=6, whose ordinate is twice its abscissa.
Q2. How many solution(s) of the equation 3x+2=2x-3 are there on the
i) Number Line ii) Cartesian plane
Q3. Draw the graph of the equation represented by the straight line which is parallel to the x-axis and 3 units
above it.
Q4. Find the solutions of the linear equation x+2y=8, which represents a point on i) x axis ii) y-axis
Q5. For what values of c, the linear equation 2x+cy=8 has equal values of x and y as its solution.
Q6. Give the geometrical interpretations of 5x+3=3x-7 as an equation
i) in one variable ii) In two variables
Q7. Draw the graph of the equation 3x+4y=6. At what points, the graph cut the x-axis and the y-axis.
Q8. At what point does the graph of equation 2x+3y=9 meet a line which is parallel to y -axis at a distance 4
units from the origin and on the right side of the y-axis.
Q9. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in
each case: (i) -2x + 3y = 6 (ii) x = 3y (iii) 2x = -5y
Q10. Find the value of k if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
Q11. If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a?
Q12. (i) Draw the graph of the linear equation using given Celsius for x-axis and Fahrenheit for y-axis.
F =(9/5)C + 32
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is
the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Summary

An equation in the form of ax + by + c = 0, where a, b and c are real numbers and
a and b are not both zeros is called a linear equation in two variables x and y. A
linear equation in two variables has infinitely many solutions.

The solutions of a linear equation can be obtained by substituting different values
for x in the equation to find the corresponding values of y.

The values of x and y are represented as an order pair. To plot the graph of this
equation, its solutions is found algebraically and then plot the points on the
graph.

Any linear equation of the form 'ax + by + c = 0' represents a straight line on the
graph. Every point that satisfies the linear equation lies on the line. Every point
that lies on the line is a solution of the linear equation. A point that does not lie
on the line is not solution of the linear equation.

The equation of x-axis is y = 0. Any line parallel to x-axis is of the form y = k.

The equation of y-axis is x = 0. Any line parallel to y-axis is of the form x = k.