Download Writing Linear Equations – 10 days Lesson Topics Objective

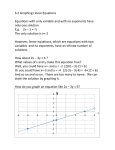
Writing Linear Equations – 10 days
Lesson Topics
Objective
Slope
 Calculate slope given
a graph.
 Calculate slope given
two points.
Example Problems
Find the slope of the line.
Common Core
Standards
2008 State
Standards
MA09-S03-C04-01
Determine the slope and
intercepts of the graph of a
linear function, interpreting
slope as a constant rate of
change
Find the slope of the line through the
given points.
 4, 5
and  5,10
Writing Linear
Equations from a
Graph
Given the graph, write
the linear equation.
Write the equation of the line.
MA09-S03-C03-03
Writing Linear
Equations given
two Points
Write a linear equation
from two points.
Write an equation of the line that
passes through each pair of points.
(3,1) and (2,4)
MA09-S03-C03-03
Write an equation given a
table of values, two points
on the line, the slope and a
point on the line, or the
graph of the line.
Write an equation given a
table of values, two points
on the line, the slope and a
point on the line, or the
graph of the line.
Writing Linear
Equations given
the slope and a
point.
Write linear equation
given a slope and a point.
Write an equation of the line that
passes through (2,1) with a slope of 3
Rate
of Change
Calculate and interpret
the average rate of
change of a function over
a specified interval.
The average rate of change of a function y =
f(x) over an interval [a,b] is
.
Basic Ex. 1
Use the following table to find the average
rate of change of g over the intervals [-2, -1]
and [0,2]:
x
-2
-1
0
2
g(x)
2
-1
-4
-10
Core Ex. 2 (Table to the right)
The table below shows the elapsed time when
two different cars pass a 10, 20, 30, 40 and 50
meter mark on a test track.
o For car 1, what is the average velocity
(change in distance divided by change in
time) between the 0 and 10 meter mark?
Between the 0 and 50 meter mark?
Between the 20 and 30 meter mark?
Analyze the data to describe the motion
of car 1.
o How does the velocity of car 1 compare
to that of car 2?
MA09-S03-C03-03
Write an equation given a
table of values, two points
on the line, the slope and a
point on the line, or the
graph of the line.
HS.F-IF.6. Calculate
and interpret the
average rate of change
of a function (presented
symbolically or as a
table) over a specified
interval. Estimate the
rate of change from a
graph.
Car 1
Car 2
d
t
t
10
4.472
1.742
20
6.325
2.899
30
7.746
3.831
40
8.944
4.633
50
10
5.348
MA09-S03-C04-02
Solve problems involving
rate of change.
Write Linear
Equations in two
or More
Variables using
Real-World
Problems.
Create equations in two
or more variables to
represent relationships
between quantities.
The cost of basic cable is $35 plus $8
per movie channel. Steve installs
cable with "m" movie channels.
What is the total cost “C” of his cable?
HS.A-CED.2. Create
equations in two or
more variables to
represent relationships
between quantities;
graph equations on
coordinate axes with
labels and scales.
MA09-S03-C03-03
Write an equation given a
table of values, two points
on the line, the slope and a
point on the line, or the
graph of the line.
MA09-S03-C02-04
Use equations, graphs,
tables, descriptions, or sets
of ordered pairs to express
a relationship between two
variables.
These standards should be evident throughout the unit (may not be in each lesson).

HS.A-REI.1: Explain each step in solving a simple equation as following from the equality of numbers asserted at the
previous step, starting from the assumption that the original equation has a solution. Construct a viable argument to justify a
solution method.

HS.A-SSE.1: Interpret expressions that represent a quality in terms of its context.
a. Interpret parts of an expression, such as terms, factors and coefficients.

HS.A-SSE.1. Interpret expressions that represent a quantity in terms of its context.