Download Chapter 13

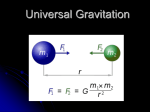
Chapter 13
Gravitation
Newton’s law of gravitation
• Any two (or more) massive bodies attract each other
• Gravitational force (Newton's law of gravitation)

m1m2
F  G 2 rˆ
r
• Gravitational constant G = 6.67*10 –11 N*m2/kg2 =
6.67*10 –11 m3/(kg*s2) – universal constant
Gravitation and the superposition
principle
• For a group of interacting particles, the net
gravitational force on one of the particles is
n 

F1,net   F1i
i2
• For a particle interacting with a continuous
arrangement of masses (a massive finite object) the
sum is replaced with an integral

F1,body 

 dF
body
Chapter 13
Problem 5
Three uniform spheres of mass 2.00 kg, 4.00 kg and 6.00 kg are placed at the
corners of a right triangle. Calculate the resultant gravitational force on the
4.00-kg object, assuming the spheres are isolated from the rest of the Universe.
Shell theorem
• For a particle interacting with a uniform spherical
shell of matter

F1,shell 

 dF
shell
• Result of integration: a uniform spherical shell of
matter attracts a particle that is outside the shell as if
all the shell's mass were concentrated at its center
Gravity force near the surface of Earth
• Earth can be though of as a nest of shells, one
within another and each attracting a particle outside
the Earth’s surface
• Thus Earth behaves like a particle located at the
center of Earth with a mass equal to that of Earth

mEarthm1 ˆ
 GmEarth  ˆ
F1, Earth  G 2
j   2
m1 j  g m1 ˆj
REarth
 REarth 
g = 9.8 m/s2
• This formula is derived for stationary Earth of ideal
spherical shape and uniform density
Gravity force near the surface of Earth
In reality g is not a constant because:
Earth is rotating,
Earth is approximately an ellipsoid
with a non-uniform density
Gravitational field
• A gravitational field exists at every point in space
• When a particle is placed at a point where there is
gravitational field, the particle experiences a force
• The field exerts a force on the particle
• The gravitational field is defined as:

g

Fg
m
• The gravitational field is the gravitational force
experienced by a test particle placed at that point
divided by the mass of the test particle
Gravitational field
• The presence of the test particle is not necessary
for the field to exist
• The source particle creates the field
• The gravitational field vectors point in the direction
of the acceleration a particle would experience if
placed in that field
GmEarth
g
2
REarth
• The magnitude is that of the freefall acceleration at
that location
Gravitational potential energy
• Gravitation is a conservative force (work done by it
is path-independent)
• For conservative forces (Ch. 8):

rf
rf
 
 Gm1mEarth 
dr 
U    F  d r     
2

r

ri 
ri
1 1 
 Gm1mEarth  
r r 
f 
 i
Gravitational potential energy
1 1 
U  U f  U i  Gm1mEarth  
r r 
f 
 i
• To remove a particle from initial position to infinity
 1 1  Gm1mEarth
U   U i  Gm1mEarth   
ri
 ri  
• Assuming U∞
=0
Gm1mEarth
U i (ri )  
ri
Gm1m2
U (r )  
r
Gravitational potential energy
Gm1m2
U (r )  
r
Escape speed
• Accounting for the shape of Earth, projectile motion
(Ch. 4) has to be modified:
2
v
ac 
 g  v  gR
R
Escape speed
• Escape speed: speed required for a particle to
escape from the planet into infinity (and stop there)
Ki  U i  K f  U f
2
m1v Gm1m planet

 00
2
R planet
vescape 
2Gm planet
R planet
Escape speed
• If for some astronomical object
vescape 
2Gmobject
Robject
 3 10 m / s  c
8
• Nothing (even light) can escape from the surface of
this object – a black hole
Chapter 13
Problem 30
(a) What is the minimum speed, relative to the Sun, necessary for a spacecraft
to escape the solar system, if it starts at the Earth’s orbit? (b) Voyager 1
achieved a maximum speed of 125 000 km/h on its way to photograph
Jupiter. Beyond what distance from the Sun is this speed sufficient to escape
the solar system?
Kepler’s laws
Tycho Brahe/
Tyge Ottesen
Brahe de Knudstrup
(1546-1601)
Johannes Kepler
(1571-1630)
Three Kepler’s laws
• 1. The law of orbits: All planets move in elliptical
orbits, with the Sun at one focus
• 2. The law of areas: A line that connects the planet
to the Sun sweeps out equal areas in the plane of the
planet’s orbit in equal time intervals
• 3. The law of periods: The square of the period of
any planet is proportional to the cube of the
semimajor axis of its orbit
First Kepler’s law
• Elliptical orbits of planets are described by a
semimajor axis a and an eccentricity e
• For most planets, the eccentricities are very small
(Earth's e is 0.00167)
Second Kepler’s law
• For a star-planet system, the total angular
momentum is constant (no external torques)
L  rp  (r )(mv )  (r )( mr )  mr 2
  const
• For the elementary area swept by vector r
2
2
1
dA
r
d

r

dA  (r )( rd )


2
2
dt
2 dt
dA
L

dt 2m
Third Kepler’s law
• For a circular orbit and the Newton’s Second law
GMm
GM
2
2
 (m)( r )   3
2
r
r
F  ma
• From the definition of a period
T
2

T 
2
4

2
2
4 3
T 
r
GM
2
2
• For elliptic orbits
4 3
T 
a
GM
2
2
Satellites
• For a circular orbit and the Newton’s Second law
2

GMm
v 
 (m) 
F  ma
2
r
 r 
• Kinetic energy of a satellite
2
GMm
U
mv


K
2r
2
2
• Total mechanical energy of a satellite
GMm
GMm
GMm
E  K U 


 K
2r
r
2r
Satellites
• For an elliptic orbit it can be shown
GMm
E
2a
• Orbits with different e but the same a have the same
total mechanical energy
Chapter 13
Problem 26
At the Earth’s surface a projectile is launched straight up at a speed of 10.0
km/s. To what height will it rise? Ignore air resistance and the rotation of the
Earth.
Questions?
Answers to the even-numbered problems
Chapter 13
Problem 2
2.67 × 10−7 m/s2
Answers to the even-numbered problems
Chapter 13
Problem 4
3.00 kg and 2.00 kg
Answers to the even-numbered problems
Chapter 13
Problem 10
(a) 7.61 cm/s2
(b) 363 s
(c) 3.08 km
(d) 28.9 m/s at 72.9° below the horizontal
Answers to the even-numbered problems
Chapter 13
Problem 24
(a) −4.77 × 109 J
(b) 569 N down
(c) 569 N up