* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 1 - Digilent Learn site
Analog-to-digital converter wikipedia , lookup
Analog television wikipedia , lookup
Waveguide filter wikipedia , lookup
405-line television system wikipedia , lookup
Amateur radio repeater wikipedia , lookup
Loudspeaker wikipedia , lookup
Atomic clock wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Spectrum analyzer wikipedia , lookup
Mechanical filter wikipedia , lookup
Rectiverter wikipedia , lookup
Regenerative circuit wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Distributed element filter wikipedia , lookup
RLC circuit wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Analogue filter wikipedia , lookup
Audio crossover wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Phase-locked loop wikipedia , lookup
Index of electronics articles wikipedia , lookup
Radio transmitter design wikipedia , lookup
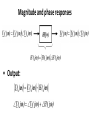
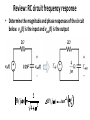
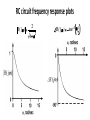
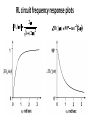
Lecture 29 •Review: • Frequency response •Frequency response examples •Frequency response plots & signal spectra •Filters •Related educational modules: –Section 2.8.1, 2.8.2 Frequency Response • Systems are characterized in the frequency domain, by their frequency response, H(j) • Magnitude response: the ratio of the output amplitude to the input amplitude as a function of frequency • Phase response: the difference between the output phase and the input phase, as a function of frequency Magnitude and phase responses • Output: Review: RC circuit frequency response • Determine the magnitude and phase responses of the circuit below. vin(t) is the input and vout(t) is the output H ( j ) 2 4 2 2 H ( j ) tan1 • Annotate previous slide to denote |H|=mag resp, <H = phase resp. Example: RL circuit frequency response • Determine the magnitude and phase responses of the circuit below. vS(t) is the input and v(t) is the output Frequency response plots • Frequency responses are often presented graphically in the form of two plots: • Magnitude response vs. frequency • Phase response vs. frequency RC circuit frequency response plots H ( j ) 2 4 2 2 H ( j ) tan1 RL circuit frequency response plots H ( j ) 2 1 ( 2 )2 H ( j ) 90 tan1 2 Signal spectra • The frequency domain content of a signal is called the spectrum of the signal • Example: v(t) = 3cos(t+20) + 7cos(2t-60) • Spectrum: 3 20 , ω 1 rad / sec V ( j ) 7 60 , ω 2 rad / sec 0 , otherwise Plots of signal spectra • Signal spectra plotted like frequency responses • Amplitude and phase vs. frequency • For our previous example: V ( j ) V ( j ) 7 20 2 , rad/sec 0 1 3 , rad/sec 0 0 1 2 3 -60 3 Graphical interpretation of system response • Plots of the input spectrum and frequency response can combine to provide an output spectrum plot • Point-by-point multiplication of magnitude plots • Point-by-point addition of phase plots • Can provide conceptual insight into system behavior Example – RL circuit response to example input Frequency selective circuits and filters • Circuits are often categorized by the general “shape” of their magnitude response • The response in some frequency ranges will be high relative to the input; these frequencies are passed • H(j) is “large” in these frequency ranges • The response in some frequency ranges will be low relative to the input; these frequencies are stopped • H(j) is “small” in these frequency ranges Filters • Circuits which select certain frequency ranges to pass and other frequency ranges to stop are often called frequency selective circuits or filters • Example: audio system graphic equalizer • The range (or band) of frequencies that are passed by the filter is called the passband • The range (or band) of frequencies that are stopped by the filter is called the stopband Specific case I – Lowpass filters • Lowpass filters pass low frequencies and stop high frequencies • The boundary between the two bands is the cutoff frequency, c • “Low” frequencies are less than c, “high” frequencies are greater than c • On previous slide, note that IDEAL filters absolutely remove all components outside the passband. • Also point out that these cannot be implemented in the real world (turns out that they would need to respond to the input before the input is applied – they need to see into the future) Specific case II – Highpass filters • Highpass filters pass high frequencies and stop low frequencies • The boundary between the two bands is (still) called the cutoff frequency, c Additional filter categories • Filters are often categorized by the order of the differential equation governing the circuit • e.g. First order filter, second order filter • Filters can also be bandpass or bandstop • A band of frequencies between two cutoff frequencies is either passed or stopped • Lowpass & highpass filters can be first or higher order • Bandpass & bandstop filters must be at least second order • We will only work with first order filters in this course Filter example 1 – Lowpass filter • RC circuit: Filter example 2 – Highpass filter • RL circuit: Non-ideal first order filters • Realizable filters do not have sharp transitions between the passband and stopband • So where is the cutoff frequency (c)? • Define the cutoff frequency where the magnitude • response is 1 2 times the maximum magnitude • Why? • The power is (generally) the square of the signal the cutoff frequency is where we have half of the maximum power (it is sometimes called the half power point) RC circuit cutoff frequency • Magnitude response: H ( j ) 2 4 2 • Annotate previous slide to calculate maximum value and frequency where we have 0.707 times maximum value RL circuit cutoff frequency • Magnitude response: H ( j ) 2 1 ( 2 )2 • Annotate to show calculation of cutoff frequency