* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Muscular System notes
Survey
Document related concepts
Transcript
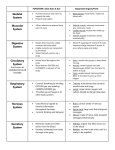
Muscular System notes (Marieb & Hoehn chapter 10) WCR Oct 2016 Know the information as specified for the muscles in the Muscles to Know list (…/notes/MusclesToKnow.docx). For the muscles in the list, you should know where they are in the body and what their actions are. Be able to identify the muscle on a picture. Be able to translate a muscle’s textbook action into a real-world activity. For example, since you know that the triceps brachii extend the elbow, then you also understand that the triceps brachii are important for doing push-ups, since elbow extension is a key part of doing a push-up. For the bolded muscles, also know their origins and insertions. For bolded muscles with multiple heads or parts, know the origins and insertions of all heads or parts. If a muscle is not on the list, it will not be on the test. We looked at four limb cross sections: two upper limb and two lower limb. It is likely that cross sectional drawings will appear on the test. Be familiar with those drawings, at the level of detail that they appear in the textbook. The test for this chapter will not include innervations (i.e. what nerve innervates what muscle). The test will not include questions about arrangement of fascicles. It will not include questions about muscle naming conventions, i.e. no questions about the meaning of word roots such as albus, brevis, rectus, etc. ____________________________ Know the basic principles of levers, force, distance from the fulcrum, and how that applies to muscles. We discussed this with examples in class. I summarize the same information below. The summary takes a lot of space, but it is not that complicated. It will not account for much of the test. If you are short on time, you may want to study this last. ____________________________ If you know the distance from the joint center to the load and the distance from the joint center to the point of muscle attachment, then you can calculate muscle force, if you are given the load. (I assume that “joint center” = “fucrum”.) Alternatively, you can calculate the load, if you are given the muscle force. The key concept we discussed in class is that of torque, which equals force times distance*. The torque exerted by the muscle equals the torque exerted by the load, if the load is not moving. The force exerted by muscle is multiplied by the distance from the joint center to the muscle attachment point, to get “torque 1”. The force of the load is multiplied by the distance from the joint center to the load point, to get “torque 2”. If the subject is supporting the load, the torques will be equal (but opposite). (The following text uses the multiplication symbol: . It displays correctly on my version of MS Word but I can’t guarantee it will display correctly for all.) Example1 Assume the patellar ligament is attached to the tibial tuberosity with an effective distance of 4 cm from the joint center of rotation, and that the quadriceps femoris muscles can pull on this ligament with 1000 Newtons of force. How much “kick-out” force (in Newtons) can the subject generate at the distal end of the tibia, 40 cm from the joint center of rotation? Answer 1 Remember that (force distance) at one location = (force distance) at another location along the tibia. In this case: (quads force) (effective distance from joint center to quads attachment point) = (distal tibial load) (distance from joint center to distal tibia). Now plug in the numbers for this particular problem: 1000 N 4 cm = (distal tibial load) 40 cm. Solve for the unknown load at the distal tibia: distal tibial load = 1000 N 4 cm / 40 cm therefore distal tibial load = 100 N. Example 2 Same system as in Example 1, but now the effective distance from the joint center to the tibial tuberosity is 3 cm, and the distance from the joint center to the distal tibia is 36 cm. The load at the distal tibia is 90 N. How much force do the quadriceps need to generate? Answer 2 Remember that force distance = force distance. In this case, (quads force) (effective distance from joint center to quads attachment point) = (distal tibial load) (distance from joint center to distal tibia). Now plug in the numbers for this particular problem: (quads force) 3 cm = 90 N 36 cm Solve for the unknown quads force: quads force = 90 N 36 cm / 3 cm therefore quads force = 90 N 12 = 1080 N. *The equation torque = force times distance assumes that the force direction is perpendicular to the line from the fulcrum (joint center) to the point of force application. In real life, and in more advanced courses, this assumption is not always true, so a more complicated equation may be needed. But in this course we will make the “perpendicular assumption” and use the simple equation above.