Download Special Relativity

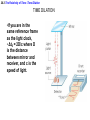
Chapter 28 – Special Relativity
What’s special about special relativity?
• In 1905, Einstein’s first paper
on relativity dealt only with
inertial reference frames
(constant velocity).
• 10 years later, he published a
more encompassing theory of
relativity that considered
accelerated motion and it’s
connection to gravity. This
was a discussion of “general”
relativity.
• His earlier work was special in
that it discussed the “special
case” of inertial reference
frames.
28.1 Events and Inertial Reference Frames
An event is a physical “happening” that occurs at a certain
place and time. Liftoff!
Reference Frame: Coordinate system in which observers
may make measurements in time and space. Anyone at
rest in the reference frame (as well as a video recorder, or
other data acquisition device) can be considered an
observer.
28.1 Events and Inertial Reference Frames
An inertial reference frame is one in which Newton’s law
of inertia is valid. An inertial reference frame can be
moving, but it cannot be accelerating. The plane moves at
constant velocity. In spite of its centripetal acceleration,
the Earth is treated as an inertial reference frame,
because the effects of its rotation and orbit are relatively
minor.
Reference Frames
•Extend infinitely far in all
directions. You can be thousands
of miles away, yet still in the same
reference frame
•Observers are at rest in their
reference frames.
•A reference frame is not the same
as a point of view. Therefore all
observers at rest relative to each
other share the same reference
frame and will view time and length
the same way.
Relative Velocity Simulation
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140
3.4 Relative Velocity without relativity
One example of an inertial reference frame is
on the ground. This observer is at rest in his
reference frame.
The train traveling at a constant speed
is another frame of reference.
Anybody sitting down in the train is an
observer at rest in their reference
frame.
3.4 Relative Velocity
An observer at rest on the ground sees the
train traveling at 9m/s relative to the ground:
vTG = +9 m/s, where + indicates to the right
(TG = Train relative to ground).
An observer at rest in the trains sees the
man on the ground traveling at
vGT = -9m/s, where – indicates to the left
(GT = Ground relative to train).
Is one of these reference frames more
“real” than the other?
Considering that the Earth revolves around
the Sun and the whole Universe is
expanding, I think not.
3.4 Relative Velocity
A passenger inside the train starts to walk up to the bar car at
the front of the moving train. Observers in their seats note that
he is traveling at vPT = +2 m/s. The passenger is moving
relative to the train’s frame of reference, therefore v PT
What is his velocity (v PG ) according to the ground-based
observer? Recall vTG is +9.0 m/s



v PG  v PT  v TG
3.4 Relative Velocity (See Chapter 3)
A passenger inside the train starts to walk up to the bar car at
the front of the moving train. Observers in their seats note that
he is traveling at vPT = +2 m/s. The passenger is moving
relative to the train’s frame of reference, therefore v PT
What is his velocity (v PG ) according to the ground-based
observer? Recall vTG is +9.0 m/s
A. + 2m/s, B. +7 m/s C. +9 m/s D. +11m/s
3.4 Relative Velocity
Same situation, but now imagine the passenger moving to the
rear of the train (that’s left). What is his speed vPG now?
A. + 2m/s, B. +7 m/s C. +9 m/s D. -7 m/s
An airplane is flying at a constant velocity, vPG = +200
m/s. In the diagram, the plane’s reference frame is
labeled S’. Two sound waves travel towards the plane.
Wave 1 travels left at vS1G = - 340 m/s, and Wave 2
travels right at vS2G = +340 m/s. What is the speed of
each wave relative to the plane (vS1P) and (vS2P) ?
vPG = +200 m/s.
vS1G = - 340 m/s.
vS2G = + 340 m/s.
Find (vS1P) and (vS2P)
vSP = vSG + vGP
vPG = +200 m/s, and vGP = -200 m/s
vS1G = - 340 m/s
vS2G = + 340 m/s.
Find (vS1P) and (vS2P)
vS1P = vS1G + vGP =-340 m/s - 200 m/s = -540 m/s
vS2P = vS2G + vGP = +340 m/s - 200 m/s = +140 m/s
Ocean waves are approaching the beach at
10 m/s relative to the ground(vWG). A boat
heading out to sea travels at 6 m/s relative
to the ground (vBG ). How fast (speed only,
not direction) are the waves moving in the
boat’s reference frame (vWB )?
A. 4 m/s
B. 6 m/s
C.16 m/s
D.10 m/s
28.2 The Postulates of Special Relativity
THE POSTULATES OF SPECIAL RELATIVITY
1. The Relativity Postulate. The laws of physics are the same
in every inertial reference frame. All inertial reference frames are
equally valid (and all are just as valid as the earth’s reference frame.
2. The Speed of Light Postulate. The speed of light in a vacuum,
measured in any inertial reference frame, always has the same value
of c, no matter how fast the source of light and the observer are
moving relative to one another.
Number 2 seems to contradict our idea of inertial reference frames.
How could this be true. Why should a light wave be different from a
sound wave?
Einstein’s Principle of Relativity
• Maxwell’s equations are considered to be laws
of physics
• Maxwell’s equations are true in all inertial
reference frames.
• Maxwell’s equations predict that electromagnetic
waves, including light, travel at speed c = 3.00
× 108 m/s.
• Therefore, light travels at speed c in all
inertial reference frames.
Every experiment has found that light travels at 3.00
× 108 m/s in every inertial reference frame,
regardless of how the reference frames are moving
with respect to each other.
28.2 The Postulates of Special Relativity
THE POSTULATES OF SPECIAL RELATIVITY
1. The Relativity Postulate. The laws of physics are the same
in every inertial reference frame. All inertial reference frames are
equally valid (and all are just as valid as the earth’s reference frame.
2. The Speed of Light Postulate. The speed of light in a vacuum,
measured in any inertial reference frame, always has the same value
of c, no matter how fast the source of light and the observer are
moving relative to one another.
The only way #2 could be true is if Δt is NOT the same in all inertial
reference frames. This was the great genius of Einstein’s Theory of
Relativity. Time and length are not always what they seem to be!
28.3 The Relativity of Time: Time Dilation
TIME DILATION
•If you are in the
same reference frame
as the light clock,
• Δt0 = 2D/c where D
is the distance
between mirror and
receiver, and c is the
speed of light.
28.3 The Relativity of Time: Time Dilation
An observer on the earth measures the light pulse traveling a greater
distance between ticks (2s > 2D). She still measures the speed of light in
the spaceship as c (postulate #2).
Therefore, her clock reads a Δt = 2s/c instead of 2D/c and Δt > Δt0
The observer in the earth’s frame of reference measures an expanded, or
dilated time.
28.3 The Relativity of Time: Time Dilation
The time interval between two events that occur at the same position is
called the proper time interval (Δt0)
In general, the proper time interval between events is the time
interval measured by an observer who is at rest relative to the
events.
In the light clock example, the proper time interval was measured by the
astronaut, because from his reference frame, both events (light leaving
source, light hitting detector) happened at the same position.
28.3 The Relativity of Time: Time Dilation
PROPER TIME INTERVAL
The time interval between two events that occur at the same position
is called the proper time interval
In general, the proper time interval between events is the time
interval measured by an observer who is at rest relative to the
events.
In the light clock example, the proper time interval was measured by
the astronaut, because from his reference frame, both events (light
leaving source, light hitting detector) happened at the same position.
leaving but not by the earth-bound observer.
t 
Proper time interval =
to
1 v c
2
to
2
Dilated time interval =
t
28.3 The Relativity of Time: Time Dilation
This is the time interval the earth-based observer
would read. Since v< c, the denominator is less than
1, so Δt (Earth-based observer time interval) is be
greater than Δt0 (astronaut observer time interval). It
can be shown that:
t 
to
1 v2 c2
From the Sun to Saturn
Who measures the proper time interval?
From the Sun to Saturn
From the Sun to Saturn
This implies it is the astronaut who measures the
proper time interval, Δt0 .
From the Sun to Saturn
From the Sun to Saturn
From the Sun to Saturn
t 
to
1 v2 c2
to find the proper time interval,Δt0
t0  t 1  v 2 c 2
Δt0 = 2310 s
From the Sun to Saturn
t0  t 1  v 2 c 2
to find the proper time interval, Δt0
Δt0 = 2310s
From the Sun to Saturn
28.4 The Relativity of Length: Length Contraction
The shortening of the distance between two points is one
example of a phenomenon known as length contraction.
Length contraction:
L0 is the proper length,
the length between 2
points measured by an
observer at rest with
respect to them.
Note that the observer
who experiences the
proper time interval, is
not the one who
measures the proper
length
v2
L  Lo 1  2
c
28.4 The Relativity of Length: Length Contraction
Example 4 The Contraction of a Spacecraft
An astronaut, using a meter stick that is at rest relative to a cylindrical
spacecraft, measures the length and diameter to be 82 m and 21 m
respectively. The spacecraft moves with a constant speed of 0.95c
relative to the earth. What are the dimensions of the spacecraft,
as measured by an observer on earth.
28.4 The Relativity of Length: Length Contraction
For this problem, the earthbound observer would determine the
distance to Alpha Centaur to be the proper length, L0, as shown in the
picture, and the observer in the spaceship would see the contracted
length.
However, it is the astronaut that sees the proper length of the
spaceship she is traveling in, while experimenters will measure it at
the contracted length.
v2
2
L  Lo 1  2  82 m  1  0.95c c   26 m
c
The distance from the sun to
Saturn
The distance from the sun to
Saturn
v2
L  Lo 1  2
c
The distance from the sun to
Saturn
v2
L  Lo 1  2
c
L = 0.62 x 1012 m
Beth and Charles are at
rest relative to each
other. Anjay runs past at
velocity v while holding a
long pole parallel to his
motion. Anjay, Beth, and
Charles each measure
the length of the pole at
the instant Anjay passes
Beth. Rank in order,
from largest to smallest,
the three lengths LA, LB,
and LC.
A.
B.
C.
D.
E.
LA = LB = LC
LB = LC > LA
LA > LB = LC
LA > LB > LC
LB > LC > LA
Conservation of momentum
• The Newtonian
momentum of an object
is defined as the product
of its mass and velocity
(mv).
• Conservation of
momentum of a system
of objects before and
after they interact, is a
law of physics that is
valid in all inertial
reference frames.
28.5 Relativistic Momentum
When the speed of an
object is close to c, the
effects of relativity must be
taken into account.
The calculation for
relativistic momentum is:
mv
p
1 v2 c2
The graph shows the effects
of relativity are not
significant until the objects
moves at some fraction of c
The relativistic momentum
is always larger than its
non-relativistic counterpart.
28.5 Relativistic Momentum
Often it is convenient to ask
for the ratio of relativistic to
non-relativistic momenta for
an object. This number can
be thought of as the
“relativistic factor” and can
be calculated as:
p
1

mv
1 v2 c2
This number is always
larger than one!
A collision of an electron with a
target in a particle
accelerator produces a
muon that moves forward
with a speed of 0.95c
relative to the laboratory.
The muon’s mass is 1.90 x
10-28 kg.
Determine the “relativity
factor”, the factor by which
the relativistic momentum is
greater than the classical
momentum.
A collision of an electron with a
target in a particle
accelerator produces a
muon that moves forward
with a speed of 0.95c
relative to the laboratory.
The muon’s mass is 1.90 x
10-28 kg. The relativistic
factor is:
p
1

mv
1 v2 c2
= 3.20
The relativistic momentum is
3.20 times that of the nonrelativistic momentum.
28.6 The Equivalence of Mass and Energy
In a short addendum to his original
paper, Einstein showed that the total
energy, and not only the kinetic
energy, of an object was dependent
on its speed and mass:
If the object is at rest relative to its
reference frame, the denominator
becomes 1 and we get the the most
famous equation in the world:
The ratio of E/E0 is the relativistic
factor:
E
mc2
1 v2 c2
Eo  mc 2
Relativistic Kinetic Energy
• It can be shown,
by use of a
binomial
expansion of the
square root term
that when v<<c,
KE = ½ mv2.
KE  E  Eo


1
KE  mc 
 1
 1 v2 c2



2
Kinetic energy and total
energy
Kinetic energy and total
energy
Kinetic energy and total
energy
Note the difference between the values for resting energy
and kinetic energy for an object moving at non-relativistic
speeds.
Kinetic energy and total
energy
For the electron, m = 9.11 x 10-31 kg, start by calculating the
relativistic factor E/E0:
E
1

E0
1 v2 c2
EXAMPLE 37.12 Kinetic
energy and total energy
28.6 The Equivalence of Mass and Energy
Example 8 The Sun is Losing Mass
The sun radiates electromagnetic energy at a rate of 3.92x1026W.
What is the change in the sun’s mass during each second that it
is radiating energy? What fraction of the sun’s mass is lost during
a human lifetime of 75 years.
28.6 The Equivalence of Mass and Energy


Eo 3.92 1026 J s 1.0 s 
m  2 
 4.36 109 kg
2
c
3.00 108 m s





m
4.36 109 kg s 3.16 107 s
12


5
.
0

10
msun
1.99 1030 kg