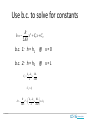Download 2d_porous_media_flow

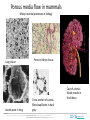
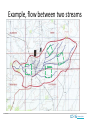
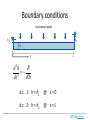
Flow Through Porous Media
• Applications and examples
• Conceptual model
• Analysis
– Governing equations
Historic picture of Thousand Springs, Idaho
– boundary/initial conditions,
– parameters
– Scaling, dimensionless numbers
• Exercise
Clemson Hydro
Sand Filter
Trap material in water
Industrial filter
Home water
filter
Sintered nickel filter
media
Sand filter for a
swimming pool
http://www.thermaxindia.com/Water-and-Waste-Solutions/Systems-and-Solutions/Filtration.aspx
http://sti.srs.gov/fulltext/ms2002431/ms2002431.html
http://www.dgssupply.dk/dgs-info/irrigation.html
http://www.poolcenter.com/filter_poolstor_pentair.htm
Clemson Hydro
High Efficiency Sand Filter
Trap material in water, reduce clogging
http://www.ameriwater.com/products/industrial/cooling-tower-filtration/
Clemson Hydro
Darcy’s Experiment
Design Water Filter
Clemson Hydro
Plants
Nutrients, heat, growth
Cross-section of a monocot root, showing cortex, pith
and vascular tissue. Image courtesy of Wendy Paul
Water flow from soil to
atmosphere through a tree
Section through woody tissue, showing xylem tracheids.
Image courtesy of Roberta Farrell.
http://ugt-online.de/en/produkte/oekologie/saftfluss-und-wasserpotenzial/xylemflusssensor-hfd.html
http://sci.waikato.ac.nz/farm/content/plantstructure.html
http://serc.carleton.edu/eslabs/weather/1d.html
Clemson Hydro
Two-way porous media flow in plants
Sap flow meter
[Kent, 2000]
Water with inorganic nutrients flows from
roots to leaves through xylem, sugar
produced in leaves flows down the phloem.
http://kids.britannica.com/elementary/art66141/Cross-section-of-a-tree-trunk
Clemson Hydro
Porous media flow in mammals
Many essential processes in biology
Lung tissue
Aveola pore in lung
Pores in kidney tissue
Cross-section of aveola.
Blood capillaries in dark
grey
http://www.scielo.cl/scielo.php?script=sci_arttext&pid=S0717http://www.sciencedirect.com/science/article/pii/S109564330000218X
95022009000300024&lng=en&nrm=iso&ignore=.html
http://www.nature.com/pr/journal/v55/n2/fig_tab/pr200444f8.html
Cast of arterial
blood vessels in
the kidney
Clemson Hydro
Rock and sediment
Recovery of important resources
•
Original void space
Photomicrograph of carbonate rock,
blue is pore space
Photomicrograph of Nubian sandstone
Christopher Kendall, 8/17/2005 ,http://strata.geol.sc.edu
[email protected]
Beach sand, Rodeo Beach, CA
http://www.msnucleus.org/membership/html/k-6/rc/rocks/3/images/rckr06.jpg
Vesicular basalt, Hawaii
meteorites.wustl.edu/id/vesicles.htm
Clemson Hydro
Pore space in Sandstone
From x-ray tomography
22 percent porosity
7 percent porosity
1 mm
Clemson Hydro
3-D Pore space with computed tomography
http://www.netl.doe.gov/newsroom/labnotes/2010/11-2010.html
Shale
Connected pores: red
Disconnected pores: green
Main flow path: blue
Sandstone
Connected pores: white
Disconnected pores: red
Image size: 1.2 mm
Clemson Hydro
Shale
SEM
CT
micron
Clemson Hydro
Aquifers and confining units
Clemson Hydro
Oil and Gas Reservoirs
Interbedded gravel, coarse- and finegrained sand stone
Spindletop well, TX
http://www.sjvgeology.org/history/lakeview/spindletop_bg.jpg
http://www.southampton.ac.uk/~imw/Oil-South-of-England.htm
Clemson Hydro
Analyze fluid flow
through porous media
Objective: Determine flux and pressure
1.Conceptual model
2.Governing Equations
3.Boundary Conditions
4.Properties
5.Examples
Clemson Hydro
General Concepts
• Average properties over REV, REV>>pores
continuum
• Mass of fluid is conserved
• Momentum is conserved
Clemson Hydro
Continuum
Representative Elementary Volume
REV
Average the effects of complex pore geometries
Clemson Hydro
Average Properties over REV
Porosity
1
0
REV Size
Use volume average of properties
Clemson Hydro
Governing Eqns
Problem: Flux and pressure are unknowns. They are what we want to
determine.
Approach: Two unknowns, need two governing equations
1. Conservation of momentum
2. Conservation of mass
Implementation:
1. general expressions first, then tailor them for porous media
2. Start here:
c
S
t
= flux vector
 
c =quantity per unit vol
S =source
Divergence of flux vector plus rate of storage change equals the rate of source production
Clemson Hydro
Conservation of Mass
c
S
t
= D +A
 
M
c 3
Lc
Storage
Advective Flux
c = rfSe
 M L3p L3f   M 
 3 3 3  3 
 L f Lc Lp   Lc 
A = qc/(fSe) =qr
r: fluid density
F: porosity
Se : degree of saturation
c rf Se

t
t
 L3f M   M 
A  qr   2 3    2 
 LcT L f   TLc 
No Diffusive Flux
Source
Governing
S=M
   rq 
rf S e
M
t
Clemson Hydro
Conservation of Momentum
c
S
t
= D +A
 
Mv
c 3
Lc
Storage
c = rv
A= vc= vvr
Diffusive Flux
D  
Governing
Lc  L f
 M Lc   MLc 
 3
 3 
 L f T   TLc 
Advective Flux
Source
Use pore
only as CV
Lc Lc M
M

T T Lc 3 T 2 Lc
c r v

t
t
Units of stress or pressure
 yx  
SF
 yx  r
   r vv    
r v
F
t
r vx
y
vx
v
 x
y
y
D  
Clemson Hydro
   r vv    
r v
F
t
v F
   v  v  P     
r
r
t r
1
1
Slow (laminar) flow with no acceleration or body forces
v F
   v  v  P     
r
r
t r
1
1
P  
P  
average
P   P
  
  
1
V
    dV
1
1
   dV 

V
V
   ndS 
Apore
w
d
Gauss’s Theorem
Clemson Hydro
P    
dP G  q
 2
dx
d
P
d2
dP   d

 x
P
dx  4

4

d
Hagen-Pouiselle Law for
laminar flow in tube
2
 dx
Force balance on a differential fluid element
with a circular cross-section
dP
4

dx
d
Force balance

d
  

d


G q
4d 2
G q
 P
4d 2
q  G
d2

Substitute into HP
Sub into average
P
Clemson Hydro
q  G
q
k

P
d2

Darcy’s Law for
horizontal flow
Need to include gravity for vertical flow
F  r g z
Body force in fluid
Need to start from two slides
ago and revise. The result is
q
k

 P  r gz 
P
In terms of hydraulic head
P
z
rg
k
q   H
H

q   K H

K k

Darcy’s Law is conservation of momentum averaged over the REV
Clemson Hydro
Things you need to know to define a process
Governing equations
Conservation Laws, constitutive equations
Define dependant variable(s)
Possibly multiple, coupled
Boundary conditions
Dirichlet, Neumann, Cauchy-type, other;
names vary with process
Properties
Constant
Spatially variable (heterogeneous)
Temporally variable, controlled externally
Temporally variable, coupled to dependent variable
Sources
Constant
Spatially variable (heterogeneous)
Temporally variable, controlled externally
Temporally variable, coupled to dependent variable
Clemson Hydro
Implementation
Hydraulic head as dependent variable
• Governing Equations
– Mass balance
  ru  Qm
rSs
steady state
h
   ru  Qm
t
transient
– Momentum balance—flow law
u
krg

h
Darcy's Law
Properties
r: fluid density [M/L3]
Ss: specific storage [1/L]
k: permeability [L2]
g: gravity acceleration [L/T2]
: viscosity [M/LT]
Source
Qm: mass source [M/(L3T)]
– Dependent variable
• Hydraulic head, h = p/ + z
[L]
z: upward coordinate [L]
u: volumetric flux vector [L/T]
Clemson Hydro
Defining Flow through Porous Media
Pressure as dependent variable
• Governing Equations
– Mass balance
  ru  Qm
rSs
steady state
h
   ru  Qm
t
transient
– Momentum balance—flow law
u
krg

 p  r gD 
Darcy's Law
Properties
r: fluid density [M/L3]
Ss: specific storage [1/L]
k: permeability [L2]
g: gravity acceleration [L/T2]
: viscosity [M/LT]
Source
Qm: mass source [M/(L3T)]
– Dependent variable
• pressure, p
[M/LT2]
D: upward coordinate [L]
u: volumetric flux vector [L/T]
Clemson Hydro
Boundary Conditions
All external boundaries
• Dirichlet (specified head/pressure)
• Neumann
h  C1
[ L]
p  C1
[ M / LT 2 ]
(specified gradient or flux)
n  u  C1
n u  0
• Cauchy
n
[L / T ]
no flow [ L / T ]
n.u
(head dependent flux)
n  u  C1h
[L / T ]
n unit vector normal to boundary
u flux vector
C1 known function
Clemson Hydro
Initial Conditions
•
•
•
•
Transient problems
Must specify values of c (head or pressure) at t=0.
Base on info about the problem, conditions at the start
i.c. not needed for steady state.
• One strategy is to run a steady state problem and use
the results as initial conditions for transient problem
Clemson Hydro
Properties
Properties
r: fluid density [M/L3]
k: permeability [L2]
g: gravity acceleration [L/T2]
: viscosity [M/LT]
cs: compressibility [1/P]
Hydraulic conductivity
K k
rg

Needed for transient models only
• Assume properties are constant for basic problems (saturated, locally
deformable).
• Properties vary as functions of h or p if unsaturated, non-local
deformation
Clemson Hydro
Fluid Properties
Depend on P, T, C, other. Values for standard conditions
Viscosity of liquids
(at 25 °C unless otherwise specified) wikipedia
Liquid :
water
sulfuric acid
[24]
Viscosity
[Pa·s]
Viscosity
[cP=mPa·s]
8.94×10−4
0.894
2.42×10
−2
1.945×10−3
propanol[24]
pitch
2.3×10
olive oil
8
nitrobenzene
81
1.863×10
motor oil SAE 40 (20 °C)
[13]
−3
0.319
mercury
1.526×10
liquid nitrogen @ 77K
1.58×10
HFO-380
2.022
glycerol (at 20 °C)
ethylene glycol
[24]
ethanol
corn syrup
castor oil
benzene
acetone
[25]
[24]
−3
−4
1.2
1.61×10
−3
Kinematic viscosity.  = r
1 Stoke =10-4m2/s
water: 10-6 m2/ s = 1centiStoke.
air: ~10x10-6 m2/ s
0.158
16.1
Density, r
at standard P and T
rwater: 1000 kg/m3
rair: 1.2 kg/m3
1.074
1380.6
0.985
3.06×10
Dynamic viscosity.  Depends on te
1 Poise = 0.1 Pa s
at standard PT conditions,
water: 0.001 Pa s = 0.01 Poise = 1 cen
air: 1.8x10-5 Pa s = roughly 1/50 of wa
1.526
1200
−2
1.3806
6.04×10
0.544
2022
1.074×10
[24]
[24]
[24]
65
5.44×10−4
[24]
1.863
319
motor oil SAE 10 (20 °C)[13] 0.065
methanol[24]
1.945
2.3×1011
.081
[24]
24.2
985
−4
−4
0.604
0.306
http://www.engineeringtoolbox.com/liquids-densities-d_743.html
Clemson Hydro
Porous media properties
-1
Darcy
–6
–7
– 2.6×10
Plastic clay
2×10
Stiff clay
2.6×10
Medium-hard clay
1.3×10
Loose sand
1×10
Dense sand
2×10
Dense, sandy gravel
1×10
Rock, fissured
6.9×10
Rock, sound
<3.3×10
Water at 25 °C (undrained)
[2]
β (m²/N or Pa )
Material
milliDarcy
microDarcy
Vertical, drained compressibilities
[3]
–7
– 1.3×10
–7
–7
– 6.9×10
–8
–7
– 5.2×10
–8
– 1.3×10
–8
– 5.2×10
4.6×10
–8
–8
–9
–10
– 3.3×10
–10
–10
http://faculty.gg.uwyo.edu/neil/teaching/geohydro/lect_images/FIG6_5.JPG
Clemson Hydro
–10
Units
•
•
•
•
Default is SI: m, kg, s, Pa
Write with square brackets: 23[m] 12[Pa]
Can change units system
Using units helpful, but not required. Orange
color on equation indicates problem with units.
• Recommend using SI
• Water density: 1000 [kg/m^3]; viscosity: 0.001
[kg/(m*s)]; g: 981 [m/s^2]
Clemson Hydro
Examples
•
•
•
•
Steady flow between two streams
Transient flow between two streams
Transient flow to a well
Transient flow in a tree
Clemson Hydro
Example, flow between two streams
What is the hydraulic head and flow between two streams?
K=1E-6 m/s; recharge R=1E-9 m/s; thickness b=10m. Qm = R*density/b
Stream
CH boundary
1000 m
Clemson Hydro
Boundary conditions
Conceptual model
h1
h2
b
L
x
2
d h
R

2
dx
Kb
b.c. 1: h = h1
@ x=0
b.c. 2: h = h2
@ x=L
Clemson Hydro
Use b.c. to solve for constants
R 2
h
x  C1 x  C2
2 Kb
b.c. 1: h = h1
@ x=0
b.c. 2: h = h2
@ x=L
C1 
h2  h1 RL

L
2 Kb
C2  h1
h
R 2  h2  h1 RL 
x 

 x  h1
2 Kb
2 Kb 
 L
Clemson Hydro
Substitute constants and solve for h
Assume L=1000m, b=25m
h
R 2  h2  h1 RL 
x 

 x  h1
2 Kb
2 Kb 
 L
RL2  x  
RL2  x
h
  h1
     h2  h1  
2 Kb  L  
2 Kb  L
2
2
RL2   x 
x 
x
h


  
   h2  h1   h1
2 Kb   L  L 
L
2

x
x
 x

h  R        h2  h1   h1
L
  L  L


*
R L2
R 
K 2b
*
Clemson Hydro
Exercise, steady state
1. Determine heads using specified geometry
and parameters
– Plot heads as color flood, contours
– Plot flow vectors, streamlines
2.Include head gradient in stream using
h=y*0.02 on boundary. Repeat above
Clemson Hydro
Exercise, Transient
Include “Storage Model,” Same properties as above. “user defined”
Storage Model, S=1E-8 1/Pa
Assume h=0 as initial conditions (default)
h=1 at boundary. This will cause pressure wave to propagate from left
to right.
R S h
  K h    
b b t
b.c
h=0
i.c.
h=1
1000 m
Run transient 0<t<3E7s.
Plot head along cross section normal to boundaries
Clemson Hydro
Verify transient problem




x
h  ( ho  hi ) 1  erf (
)   hi

K 
2
t 

Ss 

Clemson Hydro
Steady State as Initial Conditions
The previous transient example assumed initial
conditions were uniform, h=0. What if the initial
conditions were actually the steady state
conditions?
Add new study, stationary. Set up conditions for
stationary model, solve.
Then change b.c. (raise the head along boundary).
Change transient study solver configuration
dependent variables initial values of variables
solved forselect the stationary solution. See
following screen capture.
Clemson Hydro
Transient pumping test
• In the field: pump well at constant rate,
measure pressure as function of time.
• Simulation: pump well at constant rate,
simulate pressure, adjust parameters until
simulations match field data.
Clemson Hydro
Pumping rate 7 cfm,
Radial distance to monitoring well, r = 50 ft,
Aquifer thickness, b = 25 ft
Distance to stream L=150 ft
Assume rwell = 0.25 ft
Example
150ft
Drawdown at well = 90 ft at t=1000 minutes.
Determine T, K, and S
Well efficiency, Specific capacity
data
minutes
1
10
50
100
200
500
1000
1010
1020
1100
1300
1600
2000
dtw dtw-initial
10.03
0.0
12.50
2.5
17.97
8.0
20.74
10.7
23.61
13.6
27.47
17.5
30.42
20.4
26.17
16.2
24.31
14.3
19.08
9.1
15.61
5.6
13.76
3.8
12.66
2.7
T = 0.13 ft2/s
S = 0.001
Well efficiency: 0.73
T
2.25Tto
r2
0.183Q
(slope)
S
Q

Ptotal
2 T
 2L 
ln  
 rw 
Clemson Hydro
Flow in a tree
Clemson Hydro