Download Chapter 3 Lecture notes

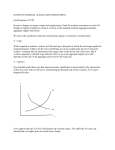
Chapter 3 Lecture notes
The classical model (I)
Essentially a supply side model. GDP is determined on the supply side of the economy.
The demand side only determines how this GDP is distributed.
We assume that the economy is characterized by a perfectly competitive model
1. There are a large number of buyers and sellers. No buyer or seller can set prices,
they must take what the market determines to be the equilibrium price. If they try
to sell above the equilibrium price they sell nothing. I guess they could sell below
market price, but why would they?
2. A buyer or seller can either take the market determined price or go away.
3. Perfect information – all buyers and sellers know what the market determined
price is precisely.
4. Workers are homogenous production units. Each worker produces the same
output per hour and each one earns the same wage W.
Production
y  y( K , N )
K  a fixed amount of capital
N  the amount of labor hours used
We will use short run models in this course. Only 1 variable factor – labor. Can’t change
capital.
See how output, y, changes as we vary the amount of labor
1
Figure 3—1 A production function for a firm showing that
y
decreases as N increases
N
Fig. 3—1 show a hypothetical production function for a firm. In this figure y
represents the amount of output that can be produced for a given amount of labor (in
terms of hours) input . Let y indicate the change in output for a given change in
labor input N . Here we will only assert that this assumption seems reasonable.
Because the amount of capital that the workers have to use is fixed we would expect
to find the amount of output that can be obtained by the purchase of an additional
hour of labor should increase with the amount of labor hired. If this were not true one
would have to ask what good does the capital do?
The demand for labor—nominal wages
We have assumed the economy is described by the competitive model. This means
that firms do not have any control over prices. The only choice the a firm can make
is how much output to produce. The competitive model also assumes that firms are
profit maximizers. The profit maximizing condition for a competitive firm is
2
W  P  MPN
MPN  Number of units of output an additional hour of labor can produce
(called the marginal product of labor)
P  Price per unit of output
P  MPN  value of output produced by an additional hour of labor
(called the value marginal product)
W  wage rate = cost of that additional hour of labor
Terms:
y
 the marginal product of labor . This shows how much output can be
N
created using an additional unit of labor.
MNP 
P MPN  the value marginal product. This is what the additional output can be sold
for – that is the nominal value of the marginal product of labor.
Example: If W=$10, P=$5, MPN=4 units, then W=$10 < P*MPN=$20. The firm
should hire that unit of labor because it will cost $10.00 but it will produce $20.00 worth
of output. The firm should hire while W  P MPN .
Suppose that W  $10, P  $5, and MPN  1 and the firm must decide whether to
purchase that unit of labor. The hour of labor will cost $10.00 but will only produce
$5.00 worth of output. So the firm shout not hire additional labor if W  P MPN .
Profit maximizing condition for a competitive firm
W  P MPN
N  MPN 
N  MPN 
Some relations between real and nominal values
If W=$10 and P=$10, then W/P=1. If W=$20 and P=$20 then the real wage is
unchanged. The paycheck workers receive will be doubled, but the price they must pay
for goods also doubled so households are no better off. If W=$10 and P=$5 then
household could buy twice as much as they could with the initial situation. The paycheck
stays the same but can buy twice as much.
3
Figure 3—2 The labor demand curve where the price level is fixed.
We will use the profit maximizing condition to derive the demand for labor curve as
shown in Fig. 3—2.
Figure 3—3. The start of the demand for labor curve.
First we will suppose that the firm is initially maximizing profits by hiring N1
amount of labor where the wage rate is W1 and the price level is P1 . Pick a point on
the graph somewhere to start with as shown in Fig. 3—3. The location of the initial
4
point is arbitrary. What we want to so is see what happens as W changes. This initial
point is a profit maximizing point
W1  P1 MPN ( N1 )
where MPN ( N1 ) is the marginal product of labor if N1 hours of labor are used.
Now we want to let something (only one thing) change. It could be either W or P but
not both. We will first see how we can represent the effect of a change in W and then
look at the effects of a change in P.
Suppose that W falls from W1 to W2 . If
W1  P1 MPN ( N1 )
then
W2  W1  W2  P1 MPN ( N1 ) .
We were at a point where the cost of an hour of labor was just equal to the value that that
hour of labor could produce. If the wage rate declines, then the firm is no longer
maximizing profit. It can make additional profits by hiring additional hours of labor and
producing more output until if reaches a new maximizing point where
W2  P1 MPN ( N 2 )
It must be the case that MPN ( N 2 )  MPN ( N1 ) . This follows because W2  W1 . The
requirement that MPN ( N 2 )  MPN ( N1 ) means that N 2  N1. Note here that we have
kept the price level fixed at P1 . We represent the labor demand curve as N d W ; P1 
where N is the number of hours of labor, d indicates this is a demand curve. The P1 after
the semicolon indicates that this is a curve where the price level is fixed at some value,
call it P1 . The labor demand curve shows how the firms demand for labor changes as the
wage rate changes.
5
Figure 3—4 The demand for labor curve in terms of nominal wages with the price level
fixed at P1 .
Next we will see how to represent the effects of price changes on the labor demand curve.
Start with some point on an existing demand for labor curve, say N d W ; P1  as shown in
Fig. 3—5. Recall we can only let one thing change at a time, so we will hold the nominal
wage rate fixed at W1 . The firm will be maximizing profits at N1 at the point W1 , P1  .
Note that all the points on the curve are combinations of wage rates and hours where the
firm maximizes profits. So at that point W1  P1 MPN ( N1 ) . Now suppse that the price
level increases from P1 to P2 . The firm will no longer be maximizing profits at W1 , P1 
because P2  P1  W1  P2 MPN  N1  . To restore profit maximization the firm must
restore equality between the wage rate and the value marginal product.
Equality can be restored by either reducing the nominal wage rate or reducing the value
marginal product. The firm cannot reduce the nominal wage rate (why?), so it must
reduce the value marginal product. The firm can’t reduce P (why?) either, so it must
reduce MPN. The firm reduces MPN by hiring more labor, increasing output, and
earning more profits until it reaches the profit maximizing output level of labor use given
by W1  P2 MNP( N2 ) . We designate the new demand for labor curve by N d (W ; P2 ) .
Note that the price variable shifts the curve. Changes in W are represented by changes
along the labor demand curve. Any other change must be represented by a shift of the
labor demand curve.
6
Figure 3—5. Changes in the price level shift the demand for labor curve in terms of
nominal wages
The demand for labor—real wages
At times it is more convenient to look at the labor market using real wages rather than
nominal wages. In that case the profit maximizing condition is
W
 MPN ( N )
P
or when the real wage is equal to the marginal product of labor. Let’s start with a graph
where the firm is maximizing profits at (W / P)1  MPN ( N1 ) as shown in Fig 3—6. As
with the case of nominal wages we arbitrarily start at some point on the graph. Suppose
now that the real wage decreases to W / P 2 . So if
W 
   MPN  N1 
 P 1
then
W  W 
   
 P 2  P 1
means that
W 
   MPN ( N1 )
 P 2
and the firm must establish equality between the real wage rate and the marginal product
of labor. If the firm hires more labor it will keep increasing profits up the point where
W 
   MPN ( N2 )
 P 2
7
as shown in Fig. 3—7.
Fig. 3—6 The initial point of the labor demand curve in terms of real wages.
Either one of two things can cause a change in the real wage. The nominal wage can
change or the price level can change. In the real wage case a change in the price level
does not shift the demand curve. A change in the price level changes the real wage and
in represented by a move along the labor demand curve.
8
Figure 3—7. The demand for labor curve in terms of real wages.
The supply of labor
Labor supply using real wages
In determining the workers choice of how much labor to supply we picture workers as
choosing between income and leisure. One can get more income supplying more hours
to the labor market, but this means the loss of leisure. One can get more leisure by
working less, but then the worker must accept a smaller income. There are two kinds of
tradeoffs to be considered. The first is the tradeoff the worker can make. The second is
the tradeoff the worker is willing to make.
9
Figure 3—8. Budget constraint curves in terms of real wages.
First consider the tradeoff the worker can make. We will consider the amount of income
the worker can earn in a day by providing different combinations of work—leisure. If the
worker works 0 hours and takes 24 hours of leisure he will receive 0 dollars of income.
If he works on hour he will receive a payment (W/P) if that is the market wage rate. If he
works 2 hours the payment will be 2(W/P). If he works 24 hours a day the payment will
be 24(W/P). These are constraints imposed on the worker. These are the substitutions
that he can make between income and leisure. Budget constraint lines for two different
real wage rates are shown in Fig. 3—8.
10
Figure 3—9 The income—leisure tradeoff . This is the tradeoff the worker is willing to
make
The other kind of tradeoff is the one workers are willing to make. This kind of tradeoff is
represented by indifference curves such as those shown in Fig 3—9. Consider the
indifference curve labeled U1 in Fig. 3—9. Any point on that curve will give the worker
a certain level of satistaction. That level of satisfaction is the same for any point on U1 .
The same holds for any point on U 2 as well. Workers would prefer any point on U 2 to
any point on U1 , however. Note that for any indifference curve if you have a large
amount of income, then you would be willing to give up a fairly large amount to get a
small addition of leisure. If you have a low level of income, you would have to receive a
very large amount of leisure to give up any of that income.
11
Figure 3—10. The worker maximizes satisfaction where the budget constraint line is
tangent to the indifference curve.
It should not be too surprising that workers optimize their leisure—income choice when
the tradeoff they can make is just equal to the tradeoff they are willing to make. That
optimum is shown in Fig. 3—10. The worker gets the maximum satisfaction possible
where the budget constraint line is just tangent to the indifference curve. The worker
cannot reach a higher indifference curve even though he would like to (the budget line
prevents this). While the worker could reach any point inside the budget constraint line,
he would not obtain a level of satisfaction inside the line that he can obtain where the two
lines are tangent. Hence the worker receives the maximum level of satisfaction by
providing N1 hours of work earning W1 N1 income.
12
Figure 3—11 The worker responds to an decrease in the real wage rate by supplying less
labor
Now consider Fig. 3—11. Suppose that the initial conditions are that the wage rate is
W / P 1 . The worker will receive the maximum level of satisfaction by providing N1
hours of labor. Suppose that the wage rate drops to W / P 2 . In that case the worker
will receive the most satisfaction possible by providing N 2 of labor. Note carefully that
a decrease in the real wage rate led to a decrease in the number of hours the worker is
willing to provide. The worker would prefer more leisure now.
13
Figure 3—12. The labor supply curve in real terms for the worker.
The labor supply curve for this worker is derived in Figure 3—12. If the real wage
decreases then the worker will be willing to supply less labor for the reduce wage. Both
the nominal and the real wage have decreased. The real wage has decreased because the
price level has remained unchanged. Next we will derive the labor supply curve using
nominal wages.
14
Labor supply using nominal wages
Figure 3—13. Budget constraint lines for two different nominal wage rates. These are
tradeoffs that workers can make.
The labor supply curve in nominal wage terms is derived by holding the price level fixed.
After we have derived the supply curve we will show how price changes can be
represented. Figure 3—13 shows the budget constraint curve letting nominal wages
change while holding the price level fixed. Here we have a decrease in the nominal wage
from W1 to W2 . Because the price level has not changed this is also a decrease in the real
wage rate. The things that we said about the workers response to a change in the real
wage rate will hold here also.
15
Figure 3—14 The worker’s response to a change in the nominal wage rate.
Now consider Fig. 3—14. Suppose that the initial conditions are that the wage rate is W1 .
The worker will receive the maximum level of satisfaction by providing N1 hours of
labor. Suppose that the wage rate drops to W2 . In that case the worker will receive the
most satisfaction possible by providing N 2 of labor. Note carefully that a decrease in the
wage rate led to a decrease in the number of hours the worker is willing to provide. The
worker would prefer more leisure now. Using this we can derive the labor supply curve.
Figure 3—15. The labor supply curve for a single worker in terms of nominal wages.
Note the price level has been kept fixed
16
To show the effects of price changes on the labor supply curve in nominal terms we will
hold the nominal wage rate fixed (only allow one thing to change at a time). Start with
the worker supplying N1 labor at W1 / P1  . Now let the price level decrease to P2 . In
this case the real wage has increased (the workers paycheck still has the same amount
written on it—he can buy more the same nominal wage).
Figure 3—16. Changes in the price level shift the labor supply curve expressed in
nominal wage terms. Note that the nominal wage rate is held fixed here.
17
Market supply and demand curves.
The supply and demand curves we derived above were for individual workers or firms.
The market curves will be the addition of these curves for a very large number of workers
or firms. Here we will show how such an aggregate curve can be derived for two
workers. The results can be generalized for any number of workers. We will just derive
a market supply curve; the market demand curve is derived in the same way.
Figure 3—17. The market labor supply curve is obtained by adding the amount of labor
supplied by each individual at a given wage rate.
As shown in Figure 3—17 we determine the amount of labor hours supplied by each
worker at wage rate W1 , Adding the hours worked for each worker determines the
market supply at W1 . The same holds for W2 and all other wage rates.
18
Output determination in the classical model
We can determine the level of output in the classical model by combining the supply and
demand for labor. The equilibrium of supply and demand will determine the actual
number of hours of labor employed and this, in turn, will determine the level of output
produced.
Figure 13—18. Output determination in the classical model. Equilibrium in the labor
market givens an equilibrium solution with N1 hours of labor employed. This leads to a
level of output of y1 using a market production function (the sum of firms individual
production functions).
19
Appendix
An Excel spreadsheet showing that P*MPN = W is the profit maximizing condition. In
this spreadsheet the production function is y  10 N 0.8 . The spreadsheet computes y,
MPN, and profit for values of N with W given.
Note that the profit is maximized at N=11 where W=20=P*MPN. A graph of profit,
wages and P*MPN is shown below. Note that profit is maximized at N=11 where
W=P*MNP.
60.0
50.0
40.0
W
30.0
profit
P*MPN
20.0
10.0
0.0
0
5
10
15
20
25
20
Example using table 3.2 in Chapter 3 in Froyen 7 ed
Change the wage rate
Change the price level
21
22