Download PLAyer: A Tool for Fast Mapping of Combinational Logic for Design

ABC:
An Industrial-Strength Academic
Synthesis and Verification Tool
(based on a tutorial given at CAV 2010)
Berkeley Verification and Synthesis Research Center
UC Berkeley
Robert Brayton, Niklas Een, Alan Mishchenko
Jiang Long, Sayak Ray, Baruch Sterin
Thanks to: NSA, SRC, and industrial sponsors,
Actel, Altera, Atrenta, IBM, Intel, Jasper, Magma, Oasys,
Real Intent, Synopsys, Tabula, and Verific
Overview
What is ABC?
 Synthesis/verification synergy
 Introduction to AIGs
 Representative transformations
 Integrated verification flow
 Verification example
 Future work

2
A Plethora of ABCs
http://en.wikipedia.org/wiki/Abc

ABC (American Broadcasting Company)


ABC (Active Body Control)


In C++, these are generic classes at the base of the
inheritance tree; objects of such abstract classes
cannot be created…
Atanasoff-Berry Computer


ABC is designed to minimize body roll in corner,
accelerating, and braking. The system uses 13
sensors which monitor body movement to supply the
computer with information every 10 ms…
ABC (Abstract Base Class)


A television network…
The Atanasoff–Berry Computer (ABC) was the first
electronic digital computing device. Conceived in
1937, the machine was not programmable, being
designed only to solve systems of linear equations. It
was successfully tested in 1942.
ABC (supposed to mean “as simple as ABC”)

A system for sequential synthesis and verification at
Berkeley
3
ABC



Started 6 years ago as a replacement for SIS
Academic public-domain tool
“Industrial-strength”



Focuses on efficient implementation
Has been employed in commercial offerings of
several CAD companies
Exploits the synergy between synthesis and
verification
4
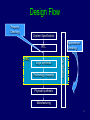
Design Flow
Property
Checking
System Specification
Equivalence
checking
RTL
Logic synthesis
Technology mapping
Verification
ABC
Physical synthesis
Manufacturing
5
Synthesis and Verification

Synthesis

Given a Boolean function
 Represented


by a truth table, BDD, or a circuit
Derive a “good” circuit implementing it
Verification
Given a (very large) circuit
 Prove that its output is always constant

6
Synthesis/Verification Synergy

Similar solutions


Algorithm migration


e.g. BDDs, SAT, induction, interpolation, rewriting
Related complexity


e.g. retiming in synthesis / retiming in verification
scalable synthesis <=> scalable verification
Common data-structures

combinational and sequential AIGs
7
Areas Addressed by ABC

Combinational synthesis




AIG rewriting
technology mapping
resynthesis after mapping
Combinational verification




SAT solving
SAT sweeping
combinational equivalence
checking (CEC)
Sequential synthesis




retiming
structural register sweep
merging seq. equiv. nodes
Sequential verification




bounded model checking
(BMC)
unbounded model/equiv
checking (MC/EC)
safety/liveness properties
exploits synthesis history
8
Terminology

Logic function (e.g. F = ab+cd)




Variables (e.g. b)
Minterms (e.g. abcd)
Cube (e.g. ab)
Logic network





Primary inputs/outputs
Logic nodes
Fanins/fanouts
Transitive fanin/fanout cone
Cut and window (defined later)
Primary outputs
TFO
Fanouts
Fanins
TFI
Primary inputs
9
AIG (And-Inverter Graphs)
Definition and Examples
AIG is a Boolean network composed of two-input ANDs and inverters
ab
00
01
11
10
00
0
0
1
0
01
0
0
1
1
11
0
1
1
0
10
0
0
1
0
cd
F(a,b,c,d) = ab + d(ac’+bc)
a
6 nodes
d
b
4 levels
a
a
c
b
c
F(a,b,c,d) = ac’(b’d’)’ + c(a’d’)’ =
ac’(b+d) + bc(a+d)
00
01
11
10
00
0
0
1
0
01
0
0
1
1
11
0
1
1
0
7 nodes
10
0
0
1
0
3 levels
cd
b
a
c
b
d
b
c a
d
10
Structural Hashing



Propagates constants and merges structural equivalences
Is applied on-the-fly during AIG construction
Results in circuit compaction
Example: F = abc
Before structural hashing
G = (abc)’ H = abc’
After structural hashing
11
Why AIGs?
Same reasons hold for both synthesis and verification

Easy to construct, relatively compact, robust


Can be efficiently stored on disk


3-4 bytes / AIG node (1M AIG ~ 4Mb file)
Unifying representation



1M AIG ~ 12Mb RAM
Used by all the different verification engines
Easy to pass around, duplicate, save
Compatible with SAT solvers



Efficient AIG-to-CNF conversion available
Circuit-based SAT solvers work directly on AIG
“AIGs + simulation + SAT” works well in many cases
12
AIG Memory Usage

Fixed amount of memory for each node



Can be done by a simple custom memory manager
Dynamic fanout manipulation is supported!
Allocate memory for nodes in a topological order

Optimized for traversal in the same topological order



Mostly AIG can be stored in cache – fewer cache misses.
Small static memory footprint in many applications
Compute fanout information on demand
13
“Classical” Logic Synthesis
Boolean network in SIS
Equivalent AIG in ABC
f
f
z
ze
xd  yd  xy
x
z
y
ab
x
cd  cd
y
e
a
b
c
d
e
a b c
d
AIG is a Boolean network of 2-input
14
AND nodes and invertors (dotted lines)
One AIG Node – Many Cuts
Combinational AIG
f


a
b
c
d
Each AIG cut represents a
different logic node
AIG manipulation with cuts is
equivalent to working on many
Boolean networks at the same
time
e
Different cuts for the same node
15
Combinational Synthesis

AIG rewriting minimizes the number of AIG nodes
without increasing the number of AIG levels
Rewriting AIG subgraphs

Pre-computing AIG subgraphs

Rewriting node A
Consider function f = abc
Subgraph 1
Subgraph 2
A
A
a b
Subgraph 3

a
b
a c
c
Subgraph 2
Subgraph 1
Rewriting node B
a
a b
a c
b
b
c
B
a
B

c
a
a b
a c
b
c
Subgraph 2
a b
a c
Subgraph 1
In both cases 1 node is saved 16
Combinational Rewriting
iterate 10 times {
for each AIG node {
for each k-cut
derive node output as function of cut variables
if ( smaller AIG is in the pre-computed library )
rewrite using improved AIG structure
}
}
Note: For 4-cuts, each AIG node has, on average, 5 cuts
compared to a SIS node with only 1 cut
Rewriting at a node can be very fast – using hash-table
lookups, truth table manipulation, disjoint decomposition
17
Resubstitution

Resubstitution means expressing
one function in terms of others


Given f(x) and {gi(x)}, is it possible
to express f in terms of a subset of
functions gi?
If so, what is function f(g)?
f(g)
f(x)
g1 g2 g3
x


x
An efficient truth-table-based and SAT-based solution exists
Runs in seconds for functions with hundreds of I/Os

A. Mishchenko, R. Brayton, J.-H. R. Jiang, and S. Jang, "Scalable
don't care based logic optimization and resynthesis", Proc. FPGA'09.
18
Technology Mapping
Input: A Boolean network
(And-Inverter Graph)
Output: A netlist of K-LUTs implementing
AIG and optimizing some cost function
f
f
Technology
Mapping
a
b
c
d
e
The subject graph
a b
c d e
The mapped netlist
19
Library Formats for Tech Mapping

GENLIB format


Simple format used in academic tools
For each gate, lists its name, Boolean function, pin names and
order, area, pin-to-pin delays, etc
http://www.eecs.berkeley.edu/~alanmi/publications/other/SIS_paper_genlib.pdf

LIBERTY format


Elaborate format used in industrial tools
For each gate, represents all information needed for synthesis,
mapping, delay/power computation, etc
http://www.opensourceliberty.org/

ABC reads both formats but uses only a subset of
available information
20
Comparison of Two Syntheses
“Contemporary” synthesis
“Classical” synthesis


Boolean network
Network manipulation
(algebraic)






AIG network
DAG-aware AIG rewriting (Boolean)




Espresso
Don’t cares computed using
BDDs
Resubstitution
Several related algorithms

Elimination
Decomposition (common
kernel extraction)
Node minimization


Node minimization



Rewriting
Refactoring
Balancing
Boolean decomposition
Don’t cares computed using
simulation and SAT
Resubstitution with don’t cares
Note: here all algorithms are scalable:
no SOP, no BDDs, no Espresso
21
Formal Verification

Property checking


Create miter from the design and
the safety property
Special construction for liveness



p
0
Biere et al, Proc. FMICS’06
D1
Equivalence checking


Property checking miter
Create miter from two versions
of the same design
Assuming the initial state is given
The goal is to prove that the
output of the miter is 0, for all
states reachable from the initial.
Equivalence checking miter
0
D1
D2
22
Outcomes of Verification

Success


Failure


The property holds in all reachable states
A finite-length counter-example (CEX) is found
Undecided

A limit on resources (such as runtime) is reached
23
Inductive Invariant

An inductive invariant is a
Boolean function in terms of
register variables, such that


It is true for the initial state(s)
It is inductive


assuming that is holds in one
(or more) time-frames allows us to
prove it in the next time-frame
State space
Bad
Invariant
Reached
Init
It does not contain “bad states”
where the property fails
24
Inductive Invariant (cont.)


It does not matter how inductive invariant is derived!
If it is available in any form (as a circuit, BDD or CNF),
it can be checked for correctness using a third-party tool



This way, verification proof can be certified
Comment 1: If the property is true, the set of all
reachable states is an inductive invariant
Comment 2: In practice, computing the set of all
reachable states is often impossible.
In such cases, an inductive invariant is an overapproximation of reachable states.
25
Verification Engines

Bug-hunters




Provers





random simulation
bounded model checking (BMC)
hybrids of the above two (“semi-formal”)
K-step induction, with or without uniqueness constraints
BDDs (exact reachability)
Interpolation (over-approximate reachability)
Property directed reachability (over-approximate reachability)
Transformers



Combinational synthesis
Reparameterization
Retiming
26
Integrated Verification Flow

Preprocessing




Creating a miter
Computing the intial state, etc
Handling combinational problems
Handling sequential problems




Start with faster engines
Continue with slower engines
Run main induction loop
Call last-gasp engines
27
Command “dprove” in ABC












transforming initial state (“undc”, “zero”)
converting into an AIG (“strash”)
creating sequential miter (“miter -c”)
combinational equivalence checking (“iprove”)
bounded model checking (“bmc”)
sequential sweep (“scl”)
phase-abstraction (“phase”)
most forward retiming (“dret -f”)
partitioned register correspondence (“lcorr”)
min-register retiming (“dretime”)
combinational SAT sweeping (“fraig”)
for ( K = 1; K  16; K = K * 2 )







signal correspondence (“scorr”)
stronger AIG rewriting (“dc2”)
min-register retiming (“dretime”)
sequential AIG simulation
interpolation (“int”)
BDD-based reachability (“reach”)
saving reduced hard miter (“write_aiger”)
Preprocessors
Combinational solver
Faster engines
Slower engines
Main induction loop
Last-gasp engines
28
Typical Run of SEC in ABC
abc - > miter –cm r\orig\s38584.1.blif r\rrr\s38584.1_r.blif
abc - > dprove –vb
Original miter:
Sequential cleanup:
Forward retiming:
Latch-corr (I= 15):
Fraiging:
Min-reg retiming:
K-step (K= 1,I= 8):
Min-reg retiming:
Rewriting:
Seq simulation :
K-step (K= 2,I= 9):
Min-reg retiming:
Rewriting:
Seq simulation :
K-step (K= 4,I= 8):
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Latches
Networks are equivalent.
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
4162.
3777.
5196.
4311.
4311.
2280.
2053.
2036.
2036.
2036.
1517.
1516.
1516.
1516.
0.
Time =
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
Nodes
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
23649.
22081.
21743.
19670.
18872.
18867.
16602.
16518.
14399.
14399.
10725.
10725.
10498.
10498.
0.
Time
Time
Time
Time
Time
Time
Time
Time
Time
Time
Time
Time
Time
Time
=
=
=
=
=
=
=
=
=
=
=
=
=
=
0.07
0.24
2.88
0.35
0.93
13.19
0.14
1.64
0.29
14.81
0.14
1.09
0.45
11.89
sec
sec
sec
sec
sec
sec
sec
sec
sec
sec
sec
sec
sec
sec
48.16 sec
29
Combinational Equivalence Checking
(command ‘cec’)
Naïve approach
• Build output miter – call SAT
 works well for many easy problems
D1
D2
?
SAT-2
D
?
C
SAT-1
A
B
Proving internal equivalences
in a topological order
Better approach - SAT sweeping
• based on incremental SAT solving
• detect possibly equivalent nodes using
simulation
• candidate constant nodes
• candidate equivalent nodes
• run SAT on the intermediate miters in a
topological order
30
• refine candidates using counterexamples
Improved CEC (command ‘&cec’)

For hard CEC instances


Heuristic: skip some equivalences
Results in
5x reduction in runtime
 Solving previously unresolved problems

Given a combinational miter with
equivalence class {A, B, A’, B’}
Possible equivalences:
A = B, A = A’, A = B’, B = A’, B = B’, A’ = B’
A
B
A’
B’
- only try to prove A=A’ and B=B’
- do not try to prove
D1
D2
A = B, A’ = B’, A’ = B
A = B’
31
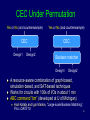
CEC Under Permutation
Yes or No (and counterexample)
Yes or No (and counterexample)
CEC
CEC
Design1
Design2
Boolean matcher
Design1



Design2
A resource-aware combination of graph-based,
simulation-based, and SAT-based techniques
Works for circuits with 100s of I/Os in about 1 min
ABC command ”bm” (developed at U of Michigan)

Hadi Katebi and Igor Markov, “Large-scale Boolean Matching”,
Proc. DATE’10.
32
HWMCC 2011

4th Hardware Model Checking Competition


Organized by


6 universities submitted 14 solvers + 4 solvers that won previous
competitions
Benchmarks


Armin Biere, Keijo Heljanko, Siert Wieringa, Niklas Soerensson
Participants


Held at FMCAD’11 in Austin, TX (Oct 30 – Nov 2, 2011)
465 benchmarks from different sources
Resources


15 min, 7Gb RAM, 4 cores
Using 32 node cluster, Intel Quad Core 2.6 GHz, 8 GB, Ubuntu
33
Courtesy Armin Biere
34
Courtesy Armin Biere
35
Courtesy Armin Biere
36
Future Work

Exploring new directions




Satisfiability Modulo Theories (SMT)
Software verification
Using concurrency, etc
Improving bit-level engines



Application-specific SAT solvers
A modern BDD package
Improved sequential logic simulators



combining random, guided and symbolic simulation
Improved abstraction refinement
… and may be a new engine or two
37
To Learn More
Visit BVSRC webpage www.bvsrc.org
 Read recent papers

http://www.eecs.berkeley.edu/~alanmi/publications

Send email


[email protected]
[email protected]
38
39