* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Analysis
Survey
Document related concepts
Transcript
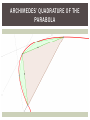
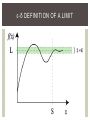
ANALYSIS History & Philosophy of Calculus WHAT IS ANALYSIS? Over the past few weeks we’ve begun to see some problems with the calculus as it was developed by Newton and Leibniz. Though it seemed to give good results, it also seemed to use dubious arguments to arrive at them. Analysis is the attempt to fix these problems and put calculus on a firm footing. This means the ideas used in its arguments must be made precise and clear, and shown to be logically consistent. Analysis is, in a sense, more philosophical than calculus. Note that in older texts (C17/18), “Analysis” is often used to mean what we mean by “Calculus”. The distinction between the two only arises in the C19/20. CALCULUS VS ANALYSIS Calculus Practical Methods(“how?”) Science & engineering Easy to learn Analysis Theoretical Proofs (“why?”) “Pure” maths Hard to learn AUGUSTIN-LOIS CAUCHY Like the Calculus itself, Analysis was arrived at by a number of mathematicians over a long period. Cauchy was one of the key early figures in this process. He did a great deal of work in both physics and pure maths. In 1821 his book, the Cours d’Analyse, was published. It is the textbook of a (reportedly very unpopular) course he taught at that time at the École Polytechnique. In this book he sought to overturn what he called the assumption of the “generality of algebra”, which had led C18 mathematicians to manipulate infinite sequences using ordinary algebra, sometimes getting absurd results. He replaced this with a rigorous notion called a “limit”, an idea already used by Newton and others but never made explicitly clear. Limits allowed some later Analysts to reconstruct calculus without referring to infinitesimal quantities. In the modern version (though not quite in Cauchy’s), infinitesimals are completely expunged. LIMITS JOHN WALLIS’S INFINITE FRACTIONS “Since, moreover, as the number of terms increases, that excess over one third is continually decreased, in such a way that at length it becomes less than any assignable quantity (as is clear); if one continues to infinity, it will vanish completely.” -- John Wallis, The Arithmetic of Infinitesimals, Prop 20. ARCHIMEDES’ QUADRATURE OF THE PARABOLA AN INFINITE SUM… ∞ 𝐴𝑟𝑒𝑎 = 𝐴 + 𝑖=1 1 4 𝑖 4 𝐴= 𝐴 3 Though the series of powers of ¼ goes on forever, when we add them we get another series that seems to converge towards the total area of all the white squares. LIMITS Both of these arguments use the same general idea. They create an infinitely long sequence of values that gradually gets closer and closer to some particular value. Since the sequence is always getting closer to that value, we say that “in the limit” it becomes equal to it. This is the definition of the limit – we don’t have to “go to infinity” to complete the sequence in order to get there. Historically, the notion of limits took a long time to crystallize and in C18 texts is often vague, like the description above. Joseph-Lois Lagrange (17361813), among others, famously lamented the lack of a clear definition of the term. LIMITS We define a limit to be the value that a sequence tends towards. For example: 1 lim = 0 𝑛→∞ 𝑛 Our intuition here is that 1/n gets smaller and smaller – closer and closer to 0 – as n gets bigger. We can make 1/n as close to 0 as we like just by making n very big. This does NOT commit us to saying something mathematically silly like 1 =0 ∞ We can countenance a process that goes on as long as we like (the potential infinite) but not an actual infinite quantity. ε-δ DEFINITION OF A LIMIT ε-δ DEFINITION OF A LIMIT The definition works like a game: I give you a sequence, s(n), and claim that its limit is L. You give me an “error”, ε, as a challenge. I can meet your challenge if I can give you a number, δ, such that for every n > δ, |s(n) – L| < ε. |x| is the “absolute value” or “size” of x – when x is negative, it flips the sign to positive. In other words, after a certain point in the sequence it is always within the margin of error defined by ε. (That is, it never leaves that small neighbourhood around L again). BUT you could give me any value of ε, no matter how small. We can keep playing this game with ε=0.1, ε=0.01, ε=0.001, ε=0.0001 and so on, and I will always have to find a point in the sequence where it never leaves that neighbourhood of L. If I can prove I can always do this, then L is indeed the limit of the sequence s(n). THE DERIVATIVE We can actually use the “converging secant lines” idea of the tangent to define the derivative using limits. Define the following sequence: 𝑠 𝑛 = 𝑓 𝑥 + 1/𝑛 − 𝑓(𝑥) 1/𝑛 Then we have: 𝑑𝑓 𝑓 𝑥 + 1/𝑛 − 𝑓 (𝑥) = lim 𝑑𝑥 𝑛→∞ 1/𝑛 Notice that 1/n is always a “proper” number, with a size – never an infinitesimal. The derivative is defined to be the value this sequence converges towards. The only way to “see” that this works is by calculating a derivative, so with apologies… Suppose f(x) = x 2 : 𝑑𝑓 𝑓 𝑥 + 1/𝑛 − 𝑓 (𝑥) = lim 𝑑𝑥 𝑛→∞ 1/𝑛 = lim 𝑛→∞ (𝒙 + Definition of the derivative. Replace f with what it actually does. 𝟏/𝒏) 𝟐 −𝒙 𝟐 1/𝑛 Multiply out the bracket. 𝒙 𝟐 + 𝟐 𝟏/𝒏 𝒙 + (𝟏/𝒏) 𝟐 −𝑥 2 = lim 𝑛→∞ 1/𝑛 2 1/𝑛 𝑥 + (1/𝑛) = lim 𝑛→∞ 1/𝑛 = lim 2𝑥 + 1/𝑛 = 2𝑥 𝑛→∞ 2 The x2 and –x2 cancel each other out. The 1/n on top and bottom cancel out. Now the limit is easy to find. CAUCHY SEQUENCES Intuitively speaking, sequences that converge to a limit must “bunch up together” around that limit in the long term. We can use this to make a definition of convergence that doesn’t need the idea of a limit. The definition is a bit unintuitive but it’s very useful in practice. A sequence is Cauchy if for every error term e, we can find an N such that, whenever n, m > N, |s(n) – s(m)| < e. In other words, “past N, everything stays bunched up in an e-sized neighbourhood”. COMPLETENESS In any continuum, every sequence that converges to a limit is Cauchy. In a “nice” continuum (technically, a “complete metric space”), every Cauchy sequence converges to a limit, and the limit is a point in the continuum. So “convergent sequences” and “Cauchy sequences” are the same objects, if your continuum is “nice” (i.e., complete). HOW TO MAKE A NICE CONTINUUM DIFFERENT CONSTRUCTIONS OF THE REAL NUMBERS Cauchy’s Cours still used infinitesimals, but tried to put them on a more rigorous footing. In the C19 quite a few attempts made to use Cauchy’s ideas to either get rid of infinitesimals or make them logically sound. Richard Dedekind saw Real numbers as arising from all the ways you could “cut” the continuum (under suitable definitions, of course). Karl Weierstrass saw Real numbers as infinite decimals. All these start from the assumption that the continuous geometric line is a coherent idea, and that it’s made up of points that can be represented by numbers. All give rise to essentially the same version of the continuum by a variety of methods. But some rest on more “fancy” arguments than others. The version we will use is the one first described by Charles Méray in his Nouveau Précis d’Analyse Infinitesimale (1872). This is the standard one used in most (though not all) introductory Analysis courses. It’s also easy to generalise beyond the Real numbers, unlike some of the others. It’s also probably the “fanciest” of all. KNOW YOUR NUMBER SYSTEM Usually we just use numbers as if they were all given to us in a lump. But it helps to sort them out and be clear about which ones we need for dif ferent jobs. The natural numbers, ℕ, are the basic counting numbers. This is fine if you just want to add and multiply. The integers, ℤ, are the negative and positive whole numbers, plus zero. This is handy if you want to be able to subtract. The rationals, ℚ, are the positive and negative fractions, plus zero. Here we can also divide. The reals, ℝ, are the numbers you need to identify the points in a continuous line. Question: are the reals and the rationals the same numbers? THE RATIONAL NUMBERS AREN’T “NICE” Our only model of a continuum so far has been the rational numbers – the fractions a/b, where a and b are whole numbers and b isn’t 0. But Cauchy sequences of rational numbers don’t always converge to a rational number limit. It’s not hard to prove that 2 is not a rational number; it’s also quite easy to produce a sequence whose limit ought to be 2. This can be repeated many times with square roots, cube roots, numbers like pi and so on. This means the rational numbers are “incomplete” – there are lots of “gaps” where there ought to be limits of Cauchy sequences. We will now, by magic, construct a number system that is complete. THE ALGEBRA OF LIMITS It turns out that the following likely -seeming things are true of Cauchy sequences: lim 𝑠 𝑛 + 𝑡 𝑛 = lim 𝑠 𝑛 + lim 𝑡 𝑛 lim 𝑠 𝑛 − 𝑡 𝑛 = lim 𝑠 𝑛 − lim 𝑡 𝑛 lim 𝑠 𝑛 × 𝑡 𝑛 = lim 𝑠 𝑛 × lim 𝑡 𝑛 lim 𝑠 𝑛 ÷ 𝑡 𝑛 = lim 𝑠 𝑛 ÷ lim 𝑡 𝑛 𝑛→∞ 𝑛→∞ 𝑛→∞ 𝑛→∞ lim 𝑛→∞ 𝑛→∞ 𝑛→∞ 𝑛→∞ 𝑛→∞ 𝑠(𝑛) = 𝑛→∞ 𝑛→∞ 𝑛→∞ 𝑛→∞ lim 𝑠(𝑛) 𝑛→∞ The things on the left are ordinary numbers – limits of Cauchy sequences. The things on the right are arithmetic operations on the limits of other Cauchy sequences. This means we can “do arithmetic with Cauchy sequences” – they “look like a number system”. THE REAL NUMBERS We now define a real number to be a Cauchy sequence of rational numbers. (Actually, this is a bit like defining a rational number to be a/b. We want 1/4 to be the same number as 2/8, so we have to do a bit more work to “group equivalent fractions together”. In the same way we want two Cauchy sequences that converge to the same limit to represent the same real number. But this is a detail.) This new model of the continuum has no “gaps” because every Cauchy sequence converges to the number that it represents ! Is this cheating? Number systems (except maybe the “natural numbers”) don’t drop out of the sky; we must construct them. Any continuum worth the name should contain all the limits of its Cauchy sequences. We just constructed it in a way that guaranteed that. And remember, the limits of Cauchy sequences obey the normal laws of arithmetic, so although its elements look a bit weird, this new continuum behaves just the way we expect it to.