Download EMR notes

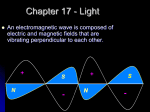
UNIT THREE – ELECTROMAGNETIC RADIATION
LESSON 1-History:
 Describe, qualitatively, how all accelerating charges produce EMR
 Explain the propagation of EMR in terms of perpendicular electric
and magnetic fields that are varying with time and travelling away
from their source at the speed of light
Faraday believed in unity in nature and that there was a
relationship between light, electricity and magnetism. He however,
lacked the mathematics to prove this.
James Clerk Maxwell, in 1860’s, developed the mathematical
theory known as the theory of electromagnetic radiation. There are 4
principles to the theory; Oersted and Faraday established the first two:
1. Oersted: An electric current will produce a magnetic field
(motor effect)
2. Faraday: A magnetic field can produce an electric current
(generator effect)
Maxwell added to these principles so that they apply to electric and
magnetic fields in conductors, insulators, and even in free space.
Maxwell’s principles are:
3. A changing electric field in space produces a magnetic field of
a magnitude that is proportional to the RATE of change of the
electric field.
BE/t
4. A changing magnetic field in space produces an electric field of
magnitude proportional to the RATE of change of the magnetic
field.
EB/t
To explain these last two principles, Maxwell used the concept of
displacement current. (movement of electrons in a substance because of
induction-this is a temporary current) To maintain a current the
conditions around the substance must continually change.
Maxwell assumed that these principles could exist in free space!! (outer
space-no atmosphere) According to his theory, a changing magnetic
field produces a changing electric field, which produces a changing
magnetic field and so on. It’s an unending sequence of events.
Since magnetic field around a current-carrying conductor depends on
the current (rate of flow of charge), a constant current would have a
constant magnetic field. If the current changes, so does the magnetic
field. Therefore, according to Maxwell’s theory, an accelerating
charged particle will produce a changing magnetic field, which will
produce the changing electric field, etc. Maxwell called this unending
sequence of events the electromagnetic wave (EMR)!!! It’s vibrating
electric and magnetic fields generate one another. The fields are
perpendicular to each other at any point and perpendicular to the
direction of propagation of the wave.
http://en.wikipedia.org/wiki/Electromagnetic_radiation
**Maxwell calculated the speed of EMR to be 3.00 x 108 m/s. Just a few
years after, the speed of light was also measured to be 3.00 x 108m/s.
Maxwell concluded that light is a form of electromagnetic radiation! (as
Faraday had suspected)
**Maxwell predicted that EMR waves of many different frequencies
could exist. All such waves would travel through space at the speed of
light and have the same properties of light; they would all reflect,
refract, diffract, interfere and be polarized.
HEINRICH HERTZ
Maxwell never produced or detected these waves, he only predicted
their existence. IN 1886, Hertz successfully did both of the above.
Using a spark gap across which electric charges move rapidly back and
forth (accelerating charged particles), Hertz generated EMR waves
whose frequency was about 109 Hz. He was able to detect these waves
some distance away using a loop of wire as a receiver (antenna). Hertz
was able to show that theses waves traveled at a speed of 3.00 x 108m/s
and have light characteristics. Hertz called these waves radio waves.
Marconi who became the first to transmit radio waves across the
Atlantic Ocean in 1901 used his discovery.
LESSON 2 – EMR SPECTRUM
 Compare and contrast the constituents of the electromagnetic
spectrum on the basis of frequency and wavelength
There is a broad range of continuous frequencies for EMR called the
electromagnetic spectrum. It may be described in terms of wavelength
and energy, as well as frequency – all of which are mathematically
related!
http://www.youtube.com/watch?v=bjOGNVH3D4Y
Visible light has a very small part of the EMR spectrum. Its range is
between 7.0x10-7 (700 nm) and 4.0x10-7 (400nm).
Recall the universal wave equation: v = 
Where v=speed of the wave (m/s)
=wavelength (m)
=frequency (Hz-revolutions per second)
This equation applies to EMR as well. The speed of EMR is given the
symbol c, which is 3.00x108 m/s.
c= Thus, the greater the frequency of EMR the lower its
wavelength. (inverse relationship)
pg 189-193
**All EMR is produced by accelerating charged particles.
Radio waves (including television signals and cell phones) and
microwaves (radar) are produced by the oscillations of electric current.
Microwaves are extremely high frequency radio waves of wavelengths
of 12.2 cm and frequency 2.45x109 Hz. It causes water molecules to
vibrate. This increases kinetic energy and therefore temperature.
Radar signals are high frequency microwaves. Cell phones use
microwaves as does satellite communication.
Infrared radiation is produced by molecular vibrations. Infrared is
associated with heat. The hotter an object, the greater the infrared
radiation coming from the object. It is used in remote controls, heat
lamps, burglar alarms, and infrared cameras.
Visible light and UV are produced by the transitions of electrons in
atoms. Visible is 400-700nm in wavelength and runs respectively from
violet, indigo, blue, green, yellow, orange and red (ROYGBIV
backwards). Ultraviolet means beyond violet and has a lower
wavelength than 400nm. It causes skin cancer and sunburn and is
blocked somewhat by the ozone layer in the atmosphere.
X-rays are produced by high-energy electrons undergoing rapid
deceleration by hitting a target. Used in medicine and airport security.
Can cause cell damage.
Gamma rays (or gamma radiation)are produced by the decaying nuclei
of unstable atoms. Carries the most energy of all EMR (lowest
wavelength – highest frequency) and therefore causes the most damage,
so it is the most dangerous. Its high energy can cause cancer, but it is
also used in medicine to destroy cancer cells (radio-therapy).
*Some of these forms may overlap in frequency and wavelength, but are
classified by their method of production (above) instead of their
fundamental properties of frequency and wavelength.
Activity:
 Determine the wavelength of EMR
Purpose: To calculate the speed of EMR (microwaves).
Background: Microwave ovens produce EMR waves by accelerating
electrons in a device called a magnetron. The electrons are accelerated
back and forth at a frequency of 2.45x109 Hz (2.45GHz). Also, reflection
of the waves within the microwave oven occurs to produce standing
waves. (draw) You can determine the wavelength of a microwave by
placing a slice of cheese in a microwave oven and microwaving it for
approximately 10s. (You may have to experiment with the time a little
bit). If the microwave oven has a rotating plate, you should remove it.
The cheese will begin to melt only at the antinodes of the standing wave.
By measuring the distance between the antinodes, you can determine
the wavelength. (Remember  = 2 times the distance between
antinodes)
Data:
Frequency of microwaves______________
Distance between antinodes______________
Microwave wavelength______________
Speed of EMR _________________
Percent error________________
LESSON THREE– SPEED OF LIGHT EXPERIMENTS



Explain qualitatively, various methods of measuring the speed of EMR
Calculate the speed of EMR, given data from a Michelson-type experiment
Design an experiment to measure the speed of light
Late 16th century: first recorded attempt to measure the speed of light. Galileo and
an assistant measured the distance across a field and took lanterns to opposite
sides. Galileo opened the lantern and when the assistant saw it they opened their
lantern. When Galileo saw the light from the second lantern he stopped the timer.
This method was not successful as the speed of light is too high and the reaction
time error was too great. v=d/t
1675: first successful measurement of the speed of light. Roemer and Huygens. A
time of astronomy. Roemer made predictions about astronomical events (Jupiter
and its moon) and for the most part was correct. However, on some occasions (6
months later) it was off by a small amount. Huygens interpreted this as the time
required for the light to travel across Earth’s orbit. The orbital diameter was
approximated and the extra time that Roemer was off by was used in the equation
v=d/t to find the speed of light. It was found to be 2.26 x 108 m/s.
19th century: it was determined that to get an accurate speed of light, long distances
or short time periods were required. Fizeau and Foucault measure the speed of
light using short time periods. A rotating slotted wheel was used and light was
passed through it and had to return through it to be seen. Adjusting the rps or rpm
of the wheel for maximum brightness, allowed for determining the speed of light.
mirror
d
Foucault used this method to measure the speed of light in water. This
measurement had great significance since particle theory of light stated that it
should speed up in water and wave theory said light should slow down in water.
Foucault found that the speed of light in water was slower than in air supporting the
wave theory.
1880: A.A. Michelson measures the speed of light using a rotating mirror and a fixed
mirror over a large distance.
light source
30 km
observer
Light reflected from the eight sided mirror to a fixed mirror 30 km away and
returned to the eight-sided mirror. When the eight-sided mirror was rotated, the
fixed mirror would receive flashes of light. The flash would return to the eight-sided
mirror and would be picked up by the viewing instrument. In order for the light to
be picked up by the viewing instrument, the eight-sided mirror had to rotate exactly
one side (1/8), two sides (2/8), etc, of a revolution while the light travelled from one
mirror to the other and back. Knowing the speed of rotation of the eight-sided
mirror, the speed of light could be calculated.
c=299,792,458 m/s. At this speed, light travels 9.46 x 1012 km in a year. This
distance is a light-year.
Michelson received a Nobel Prize for this experiment.
Pg 195-202
LESSON FOUR: PROPERTIES OF EMR
 Describe, quantitatively, the phenomena of reflection and
refraction, including total internal reflection
All forms of EMR have the same properties. Since we can view light
without additional special equipment, we will study the properties
according to light. The properties do vary, however, according to
wavelength. An example of this is that the longer the wavelength, the
greater the diffraction. (However, all EMR diffracts)
The properties of EMR include:
Reflection
Refraction
Diffraction
Interference
Polarization
1. Reflection:
Both waves and particles will reflect according to the law of
reflection: the angle of reflection equals the angle of incidence.
r = i
Plane Mirror-flat smooth mirror:
The incident ray is the incoming ray. The reflected ray is the outgoing
ray. The normal is a line perpendicular to the reflecting surface. The
angles of incidence and reflection are both measured with respect to
the normal.
Light obeys this law, however, this does not help us in determining if
light is a wave or particle since this law is a property of both forms of
energy.
Properties of the image from a plane mirror: (read pg 654-656)
Virtual Image – an image formed by diverging light rays. It is
always on the opposite side of the mirror from the object.
 Position- the image position is equal to the negative of the
object position. The negative sign indicates that the image
is virtual.
 Height- image height is equal to object height
 Orientation- the image has the same orientation as the
object (top and bottom) but has a front-to-back reversal
(mirror image-right and left are reversed).
Some of pages 203-213
Assignment:
1. If the angle of incidence of a ray of light to a mirror is 50.0o, what
is the angle of reflection from the mirror?
2. IF the angle of incidence of a ray of light to a mirror is 20.0o, what
angle does the reflected light ray make with the mirror?
3. If an incident ray of light makes an angle of 58o with a mirror,
what is the angle between the incident ray and the reflected ray?
4. A ray of light is reflected in series off of two mirrors, A and B, as
shown in the diagram below. What is the angle of reflection from
mirror B?
LESSON 5 – REFLECTION FROM CURVED MIRRORS
 Describe, quantitatively, simple optical systems, consisting of only
one component, for both lenses and curved mirrors
 Use ray diagrams to describe an image formed by thin lenses and
curved mirrors
There are two types of curved mirrors; concave and convex. Concave
mirrors have a ‘caved in’ shape: convex mirrors have a ‘pot belly’ shape.
Of course it depends which side is mirrored and which side you are
standing on!
Concave mirrors are used in reflector telescopes and satellite dishes to
reflect television signals. The mirror in the back of the drugstore is a
convex mirror. Rear view/side mirrors on some vehicles may also be
convex.
A convex mirror has a VIRTUAL focus and is called a DIVERGING
MIRROR.
A concave mirror has a REAL focus and is called a CONVERGING
MIRROR.
SPHERICAL ABERRATION – all spherical mirrors have a defect called
the spherical aberration. Rays of light parallel to the principle axis that
reflect NEAR THE EDGE OF THE MIRROR do not reflect through the
principle focal point. To correct this problem, the shape of the mirror
maybe adjusted to a parabolic shape, or their size is kept relatively
small compared to the radius of curvature. We will assume that the
mirrors are relatively small and the problem is not significant.
RAY DIAGRAMS – CURVED MIRRORS:
The position, size, and nature of an image produced by a curved mirror
can be found by a scale ray diagram. Use the following steps:
1. Draw the mirror, including its principle axis, centre of curvature,
and principle focal point.
2. Place a vertical arrow on the principle axis to illustrate the
position and size of the object.
3. Draw two rays from the tip of the object arrow to the mirror.
Choose from the following 3 types of rays:
a. A ray from the head of the object and parallel to the
principle axis that then reflects through (or appear to
diverge from) the principle focal point.
b. A ray passing through the centre of curvature and the head
of the object, which will reflect, back along the same path.
c. A ray passing through the head of the object and the focal
point (or directed at the focal point) that then reflects
parallel to the principle axis.
Where the reflected rays meet (real image) or appear to diverge
from (virtual image), is the position of the image. A vertical arrow
can be drawn from the principle axis to the meeting point
described to represent the position and size of the image.
Convex:
Concave:
Characteristics of the images:
 Real or virtual
 Erect or inverted
 Larger, smaller, or the same size as the real object
Pg 225-227
Summarize properties of images based on object positions:
The numerical values produced by ray diagrams may not be as precise as
those produced mathematically. They are used to describe
characteristics of the image.
MATHEMATICS OF MIRRORS:
To indicate the difference between images that are real or virtual, focal points that
are real or virtual, images that are erect or inverted, we need to incorporate some
sign conventions into the mathematics.
Real focal points: f (focal length) is positive
Real images: di (distance of the image) is positive
Erect images: hi (height of image) is positive
Virtual focal points: f is negative
Virtual image: di is negative
Inverted image: hi is negative
 You might note that ALL real images are inverted, and all virtual
images are erect!!!!
Formulas:
1. Magnification: M = hi/ho or di/do
where M = magnification (how many times bigger the image is than
the object)
hi= image height
ho = object height
di = image distance from the mirror
do = object distance from the mirror
therefore:
hi/ho = -di/do
* the negative sign is part of the formula and necessary!
2. Mirror equation:
1/f = 1/do +1/di
Examples:
Pg 228-229
LESSON SIX– REFRACTION AND SNELL’S LAW
 Describe, qualitatively and quantitatively, how refraction
supports the wave model of EMR using the wave equation for
refraction.
http://www.youtube.com/watch?v=FAivtXJOsiI
Refraction is the bending of a wave as it changes velocity. A change in
velocity is caused by a change in the medium (material) through which
the wave travels. Waves bend when they change medium/speed,
particles don’t.
Similar to reflection, the angles of incidence and angle of refraction are
measured with respect to the normal. However, the relationship
between the refracted angle and the incident angle is more difficult to
see. It was worked out by Willebrord Snell and is therefore referred to
as the law of refraction or SNELL’S LAW:
sin1/sin2 =v1/v2 = 1/2 = n2/n1
Where ‘n’ is a constant that compares the speed of light in the medium
to the speed of light in air or a vacuum. ( n=c/v ) This is called the index
of refraction for the medium. The greater the index of refraction is, the
greater the change in direction. Diamond has an index of 2.42 while ice
has an index of 1.31. Note that the index ratio is an inverse ratio to the
others!!!
n for air/vacuum is 1.00 and the speed of light in the same is 3.00 x
108m/s. KNOWN QUANTITIES!!
When light slows down (smaller speed), the angle will be smaller and
the wavelength will be smaller. (higher index!!)
Any time a wave hits a boundary between mediums, you get a
combination of reflection and refraction. We are going to focus on the
refraction:
What happens to the frequency of waves or light when it passes from
one medium to another?
Does a mechanical wave speed up of slow down in a denser medium?
(think water/sound waves). What does EMR do? What do particles do?
Critical angle!
When light passes from a medium that has a high index of refraction
(water) into a substance that has a lower index of refraction (air), the
light speeds up and bends away from the normal. An angle of incidence
can occur such that the refracted angle is 90o and this angle that creates
a 90o refraction is called the critical angle. Any incident light ray at an
angle bigger than the critical angle will cause reflection only! This
result is called total internal reflection. It only occurs when light from
a medium with a high index hits a barrier to one with a lower index.
Some of pages 203-213
EXAMPLES OF REFRACTION;
 A pool of water is deeper than it appears; this is because the light
waves in the water are shorter than in the air. The actual depth of
the water is 1.33 times great than the apparent depth!
 The highway ahead of you when you drive your car appears to be
wet, but you never reach the wet road; this is a mirage. The image
that you see is a reflection of the sky on the hot layer of air above
the road. The index of refraction of hot air is less than the index of
refraction of cool air; therefore, the light passes from cool air
(high index) into hot air (low index). Total reflection can occur –
you will see a reflection of the sky.
 The twinkling of stars or distant lights is due to refraction. The
direction the light travels changes as it passes through air of
different temperatures. Because this air is in motion, it will
change the position that the star or light appears to be – but only
slightly.
 You see the sun and the sunlight for a few minutes before it rises
and after it sets. Earth’s atmosphere refracts the light from the
sun.
 Fibre optics uses total internal reflection. As the light travels
down these glass fibres, it cannot escape. Light enter at one end
of the fibre and each time it strikes the surface the angle of
incidence is larger than the critical angle. The light is therefore
kept within the fibre. Fibre optics is replacing electric circuits in
communication technology, such as cable television and
telephone. Physicians can even use fibre optics to look inside
your body.
LESSON SEVEN– LENSES
Lenses work on the principle of refraction much like mirrors are
reflection. Similar to mirrors there are two types of lenses: concave and
convex.
Any lens that is thinner at the center than at the edges is a concave lens.
These lenses are ‘caved in’ on one or both sides. They are called a
diverging lens (concave is diverging!!! Backwards to mirrors!) because
when light passes through it, the light spreads out.
Any lens that is thicker at the centre than at the edges is a convex lens.
They have a pot-belly shape on one or both sides. A convex lens is a
converging lens because when light passes through it, the light comes
together. (Again! backwards to mirrors)
Eg.
Our examples will focus on double concave and double convex lenses
for simplicity, and they will be referred to as concave or convex lenses.
Because light can travel through a lens in either direction, a focal point
is indicated on both sides (principle and secondary) of the lens at the
same distance from the lens. In a convex lens the principle focal point is
a real focal point (on the refracted side), but in the concave lens the
principle focal point is a virtual focal point (on the incident ray side).
In mirrors the focal point was ½ the radius of curvature, but in lenses
the material of the lens as well as the curvature affect the distance of the
focal length from the optical centre. The lower the index of refraction of
the material the longer the focal length. The greater the radius of
curvature, the longer the focal length.
Ray Diagrams:
The position, size and nature (real or virtual) of images can be found by
a scale diagram much like mirrors. Use the following steps;
1. Draw the lens, including the principle axis and both focal points.
2. Place a vertical arrow on the principle axis to illustrate the
position and size of the object.
3. Draw two rays from the tip of the object arrow to the lens by
choosing from the following:
a. A ray parallel to the principle axis, refracting through (or
will appear to diverge from) the principle focal point.
b. A ray passing through the optical centre, which does not
change direction.
c. A ray passing through the secondary focal point (or directed
toward it), that refracts parallel to the principle axis
The point where the REFRACTED rays meet (real image) or
appear to diverge from (virtual image) is the position of the
image. If a vertical arrow is drawn from the principle axis to the
point described, the position and size of the image will be
indicated.
The characteristics of the image are described the same way as
with mirror images. I.e. Erect or inverted, real or virtual, larger
smaller or same size.
Convex:
Concave:
Pg 216-217
MATHEMATICS OF LENSES: -More accurate way to find image
characteristics
Sign conventions are the same as with mirrors:
Real focal points: f (focal length) is positive
Real images: di (distance of the image) is positive
Erect images: hi (height of image) is positive
Virtual focal points: f is negative
Virtual image: di is negative
Inverted image: hi is negative
 You might note that ALL real images are inverted, and all virtual
images are erect!!!!
Equations are the same!
Eg. 1 A glowing object 2.5 cm tall is placed 15 cm from a convex lens. If
the lens has a focal length of 7.5 cm, what
a) is the distance of the image from the lens?
b) Is the size of the image?
c) Are the characteristics of the image?
Eg. 2 A glowing 4.0 cm tall object is placed 9.0 cm from a concave lens.
If the lens has a focal length of 5.0 cm, what
a) is the distance of the image from the lens?
b) Is the size of the image?
c) Are the characteristics of the image?
Pg 218-222
Applications of Lenses and Mirrors
LESSON EIGHT– Wave Nature of Light (Diffraction/Interference
and Poisson’s Spot)
 Describe, qualitatively, diffraction, interference and polarization
 Describe, qualitatively, how the results of Young’s double-slit
experiment support the wave model of light
 Solve double-slit and diffraction grating problems using the
formulas
 Demonstrate the relationship among the wavelength, slit
separation, and screen distance using empirical data and
algorithms
In the 17th century there was debate about the nature of light. Light is a
form of energy, and energy can be transmitted by means of particles or
by means of waves. Sir Isaac Newton believed that light traveled by
particles while Christian Huygens believed that it traveled as waves.
During the 1st part of the 19th century, a number of developments
supported the wave theory. These were:




Young’s double slit experiment
The discovery of Poisson’s spot
The measurement of the speed of light in water
Polarization
DIFFRACTION:
Diffraction and wave interference are fundamental properties of waves.
Neither diffraction nor wave interference can be explained using the
particle model since particles do not exhibit these behaviors. Therefore,
it can be concluded that if light exhibits these properties, it must travel
as a wave.
Diffraction- energy bends (or spreads out) as it passes through a
small opening, or when it moves past an obstacle. From studies of
water waves, it is known that the extent of diffraction depends on the
wavelength of the wave and width of the opening. The longer the
wavelength is, the greater the diffraction; the smaller the opening, the
greater the diffraction.
Light has a very small wavelength in the order of 10-7m. Therefore, you
have to use a very small opening, or slit, in order to observe significant
diffraction.
INTERFERENCE:
Wave interference is another fundamental property of waves. Particles
do not interfere constructively or destructively.
When a crest from one source meets a crest from another source, their
energies combine to displace the medium.
Constructive interference – the amplitude of the combined waves is
larger. Destructive interference – the amplitude of the combined waves
is smaller.
If you were to look in the glass side at the end of the ripple tank, you
would see alternating constructive and destructive interference points.
This is a diffraction pattern! The maxima and minima occur in
alternating patterns.
Thomas Young applied the concept of diffraction pattern to light. In
1803, he demonstrated it with the following procedure
1. He blackened a glass slide and put two very narrow scratches on
the slide.
2. He passed monochromatic light through these scratches.
3. From this setup, Young observed a diffraction pattern on a screen.
This shows that light both diffracts and interferes and is evidence
of light as a wave. Yet, at the time light as a wave was not
accepted by all scientists.
λ = dsinθ/n
maxima/bright fringe or band/antinode
If d is small relative to l, then the angles are small and the two angles are
close to equal. At this point we can assume several things: that the two
angles are equal, and that sin θ = tan θ. Because of this, we can use the
equation λ = dx/nl but recognize that this is only accurate if the angle is
less than 100.
**maximum interference(bright spots are brightest) occurs when the
size/spacing of the opening matches the wavelength of EMR.
Diffraction gratings:
Pg237-243
POISSON’S SPOT: (see shared physics lab video)
In 1818 Fresnel wrote a paper about light as a wave and that a shadow
of a sphere illuminated by monochromatic light should have a bright
spot at the centre (due to diffraction). Poisson argued that light did not
travel as a wave and thought this idea was ridiculous. Arago tested
Poisson’s prediction and it was demonstrated that there is indeed the
existence of this bright spot. The centre of a spherical or circular object
is equidistant from all points along the circumference and therefore the
light waves should reach the centre of the shadow from all around the
circumference in phase, resulting in constructive interference (a
maxima). This only occurs, however, if the circular (spherical) object is
small enough that light can diffract to the centre. It works best if the
circular/spheres diameter matches the wavelength of EMR – maximum
diffraction and brightest spot.
LESSON NINE– POLARIZATION
Not only is there evidence that light travels as a wave but there are two types of
waves – transverse and longitudinal. Transverse waves can be polarized. Light can
be polarized. Therefore, light is most likely a transverse wave. Transverse waves
can be polarized because their particles vibrate perpendicular to the direction of the
energy flow. They therefore can vibrate in any plane and when vibrating in all
planes are called non-polarized light. When light goes through a polarizing filter, it
is restricted to one plane and therefore polarized. If two filters are used, they can be
rotated to adjust the amount of light passing through. When the filter axes are
perpendicular to each other, they block all of the light. This is evidence that light is a
not only a wave, but a transverse wave.
Much of the glare reflected from horizontal surfaces is polarized horizontally. This
is why polarized sunglasses are used to reduce glare. The polarization axis is
vertical – therefore greatly reducing the glare.
Three-dimensional movies also use polarization to give the appearance of depth.
Two pictures are taken from slightly different angles. These pictures are then
projected by using two projectors. One of these is fitted with a vertical polarizer and
the other with a horizontal polarizer. When you watch the pictures wearing
polarized glasses, one of the lenses is vertical and the other is horizontal. This
allows your two eyes to observe the original scene from slightly different angles.
This explanation for polarization was given by Young and Fresnel in 1820. Up until
that time, the wave model of light supported the concept that light travelled by
longitudinal waves.
Pg232-234
LESSON TEN – DISPERSION OF LIGHT
 Compare and contrast the visible spectra produced by diffraction
gratings and triangular prisms.
White light is composed of 7 colours of light; red, orange, yellow, green,
blue, indigo, and violet. The dispersion of light is the separation of
white light into those components. It can be separated by means of
refraction or diffraction.
Dispersion by means of refraction: The order of the colours produced by
the spectrum should show that violet is refracted the most and red is
refracted the least!
(lower λ (violet) refracts the most – it has a lower speed in glass than
higher wavelengths (red), smaller angle of refraction, larger change in
direction)
Violet and blue light also scatters more by molecules in the atmosphere
producing the image of a blue sky.
Dispersion by means of diffraction: The order of the spectrum
produced should show violet at the inside of the 1st maxima and red at
the outside of the first maxima!
(higher λ (red) diffracts the most; λ = dsinθ/n)
This is why the initial light seen from a sunrise is red/orange in color
and the last light from sunset is also red/orange as it diffracts the most
around the Earth.
Pg232-234
Wave properties review pg 246
LESSON ELEVEN – WAVE PARTICLE DUALITY
Read PG 702-705 (Pearson)
 Define the photon as a quantum of EMR and calculate its energy
 Classify the regions of the electromagnetic spectrum by photon
energy
Classical physics could not explain blackbody (incandescent – perfect
radiator of light as well as a perfect absorber of all frequencies)
radiation using wave model of light.
When hot solids and gases are heated they emit EMR. At low
temperature they emit IR and at high temperatures they emit most of
the visible spectrum as well as UV. The brightness is mainly dependent
on the temperature so that as the temperature rises the spectrum shifts
to higher frequencies. Maxwell’s theory of EMR predicts that radiation
is causes by the oscillation of electric charges (changing fields) and as
the temperature increases, so too should the intensity and frequency at
a steady rate –classical physics. However, this was not observed. In
1900, Max Planck derived an equation to describe the blackbody
radiation but in order to do that he had to hypothesize that an oscillator,
including vibrating atoms and molecules is quantized. That is, the
oscillator can only have certain values of energy. The energies allowed
are given by
E=nhf
Where E = energy
n = positive integer
h = Planck’s constant (6.63 x 10-34 Js)
f = frequency of vibration
Planck’s hypothesis was the beginning of the quantum theory.
It seemed too radical at the time and was not generally accepted. It was
compared to saying that a swinging pendulum could only have certain
energies and could only increase in height by certain intervals.
In 1905, Albert Einstein used Planck’s hypothesis to include light
energy. He explained that energy in light was not continuous but
quantized. The energy of a quantum depended on the frequency of the
light (or EMR). A ‘quantum’ is now called a ‘photon’.
E = hf or hc/λ
The quanta in the red region have lower energy than quanta in the UV
region.
This energy is often expressed in eV for photon energy and the
conversion is on your data sheet.
Planck’s theory has two important implications”
1. EMR waves do not transmit energy continuously but rather in
small packages called quanta – later known as photons
2. Physical objects do not vibrate with random energy because
the energy is restricted to certain discrete values. This is seen
only with microphysics – atomic physics. It is insignificant to
macrophysics (large body objects)
Pg252-256
LESSON TWELVE – Einstein and the PHOTOELECTRIC EFFECT
 Describe the photoelectric effect in terms of the intensity and
wavelength or frequency of the incident light and surface material
 Predict the effect, on photoelectric emissions, of changing the
intensity and/or frequency of the incident radiation or material of
the photocathode
 Describe, quantitatively, photoelectric emission, using concepts
related to the conservation of energy
 Describe the photoelectric effect as a phenomenon that supports
the notion of the wave-particle duality of EMR
 Analyze and interpret empirical data from an experiment on the
photoelectric effect using a graph
While he was doing experiments on Maxwell’s Theory of
Electromagnetic Waves, Heinrich Hertz noticed that some metallic
surfaces lost their negative charges when they were exposed to
ultraviolet light. This phenomenon was called the photoelectric effect
and the electrons emitted from the metal’s surface were termed
photoelectrons.
Many experiments on photoelectricity were performed using a Cathode
Ray Tube (CRT).
If the voltage applied is reversed then the anode becomes negative. If
the potential is then increased it is possible to ‘turn back’(stop) the
photoelectric current.
The experiments yielded several important results:
1. Electrons are only emitted when the frequency of the incident
light is above a certain value called the threshold frequency. At
this frequency or above this the frequency magnitude of the
photoelectric current varies directly as the intensity of the
light. More intense light more photoelectrons (current)
2. Below the threshold frequency there is no photoelectric
current regardless of the intensity of the light.
3. The threshold frequency is different for different kinds of
cathodes (metals)
4. As a retarding potential is increased the photoelectric current
decreases independent of the intensity of the light. From this
scientists learned that photoelectrons have different amounts
of energy. A potential can be reached that completely stops the
photoelectric current. This potential difference is called the
cut-off potential or stopping voltage, Vstop.
5. Different frequencies of light (above the threshold frequency)
have different stopping potentials. The higher the frequency of
light the higher the stopping potential. The stopping potential
is related to the maximum kinetic energy of the
photoelectrons.
(The slope of all three graphs is the same – later known to be
planck’s constant)
6. When photoelectrons are emitted the electrons are released
immediately even for weak light sources. (There was no time
needed to build up energy absorption.)
Albert Einstein proposed a new theory to account for the experimental
results. He suggested that light energy is not transmitted as a
continuous wave but rather as small packets of energy called photons
(quanta). The amount of energy in each photon was a definite amount
determined by the frequency of the light. The amount of energy in a
photon was given by E=hf.
Einstein reasoned that the electrons near the surface of a metal
(cathode) needed some energy to escape from the surface. Any extra
energy they received showed up in the electrons as kinetic energy.
(measured by the stopping voltage).
Summary:
Light
Higher frequency (color)
Higher intensity (brightness)
Photoelectron
Higher energy (voltage)
More electrons (current)
Theory: When a photon hit an electron all the energy of the photon was
given to the electron. If this energy was NOT sufficient for the electron
to escape it was re-emitted by the electron. If the energy was sufficient
then the electron could escape immediately. If the energy of the photon
was more than the electron required then it showed up as kinetic
energy in the electron (high velocity).
Photon energy  escape energy + kinetic energy of electron
(conservation of energy)
Ephoton= W + Ek electron
If the electron just escapes but has no Ek, then Ephoton= W
Voltage to stop the current can be used to find the Ek of the electron:
Vstop = ΔEk/q
Millikan showed that Einstein’s theory was correct in 1916; by
showing that the slope of the energy vs. frequency graph for any
metal was equal to planck’s constant (h).
Pg 259-267
COMPTON EFFECT-MOMENTUM OF A PHOTON
 Explain, qualitatively and quantitatively, the Compton effect as
another example of wave-particle duality, applying the laws of
mechanics and of conservation of momentum and energy to
photons.
Arthur Compton performed an experiment in 1923 in which he directed
high-energy X-rays at a metal foil. Compton noted that lower energy
(low frequency) X-ray photons were being emitted as well as electrons!
Classical electro-magnetic theory could not explain these results.
Compton’s theory was that the photon acted like a particle. When a
photon struck an electron the photon bounced off the electron but lost
some of its energy in the collision. Such a collision would be elastic –
that is BOTH momentum and energy would be conserved.
Compton used Einstein’s idea that mass was a form of energy (and vice
versa) to explain his experimental results. Einstein’s theory of relativity
(E=mc2) said that a body with energy E has a mass equivalent of
m=E/c2.
Because momentum is given by p=mv the momentum of a photon is
given by p=E/c2 times v
p=E/c
but since E=hf for photons, then p=hf/c or p=h/λ
Compton’s experiments demonstrated that particle-like property of
light or EMR – photons could exhibit mathematically, the conservation
of energy and momentum in a collision.
Compton’s Scattering Equation:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/compeq.html
where m=mass of the electron
θ=angle of scatter of the EMR (x-ray)
pg 269-276
De Broglie: (also in Unit 4)
In 1924 shortly after the discovery that EMR exhibited both wave and particle
behavior, Louis De Broglie suggested that particles might also have both wave
and particle behavior. The wavelength of a particle could be related to their
momentum.
λ = h/p for EMR
but p = mv for particles
therefore λ = h/(mv)
This is called the DeBroglie wavelength!!
This seems absurd for large masses to have a wavelength to their motion; and
because of their large mass, you can see that mathematically the λ would be near
zero. But for extremely small mass particles (like electrons) it can actually be
detected that they move with a wave motion (wavelength).
Diffraction is a characteristic of wave motion and observed for EMR, but it is also
demonstrated by electrons when they pass through a crystal or thin metal foil. They
produce a diffraction pattern!
Today, the electron microscope uses the wave nature of electrons. However, the
wavelength is extremely small. This small wavelength is used to allow us to
distinguish the detail so much more clearly with an electron microscope than with a
light microscope!
Pg 296-298
Theory of relativity:
http://topdocumentaryfilms.com/nova-the-elegant-universe/