Download Control surface Control Volume

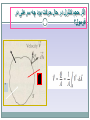
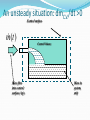
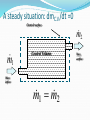
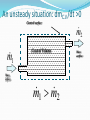
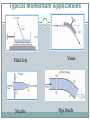
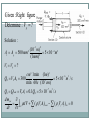
‫اگر حجم کنترل در حال حرکت بود چه سرعتی در‬
‫فرمول؟‬
‫‪+‬‬
‫–‬
‫بقای جرم‬
• Incompressible Fluids
 Steady, Compressible Flow
‫فرض یکنواخت و یک بعدی‬
‫بودن سرعت در هر مقطع‬
An unsteady situation: dmC.V./dt >0
Control surface
m (t )
Mass flow
into control
surface, kg/s
Control Volume
Mass in
system,
m(t)
A steady situation: dmC.V./dt =0
Control surface
2
m
m 1
Control Volume
Mass
inflow
1  m
2
m
Mass
outflow
An unsteady situation: dmC.V./dt >0
Control surface
2
m
m 1
Control Volume
Mass
inflow
1  m
2
m
Mass
outflow
EXP1)The balloon is being filled through section 1, where the area is A1, velocity
is V1,and fluid density is ρ1. The average density within the balloon is ρb(t). Find
an expression for the rate of change of system mass within the balloon at this
instant.
‫با توجه به پروفیل سرعت داده شده برای‬
‫جریان درون لوله‪ ،‬سرعت متوسط را‬
‫محاسبه کنید‪.‬‬
‫)‪EXP2‬‬
EXP3)
Use the triangular control volume in Fig., bounded by (0, 0),(L, L), and
(0, L), with depth b into the paper. Compute the volume flow through
sections 1, 2, and 3, and compare to see whether mass is conserved.
V = Ui; U=30 m/s.
The boundary-layer thickness at location d is δ=5 mm. The fluid is air with density ρ=1.24
kg/m3. Assuming the plate width perpendicular to the paper to be w=0.6 m, calculate the
mass flow rate across surface bc of control volume abcd.
‫هر یک از سرعت ها چه‬
‫مفهومی دارند؟‬
Typical Momentum Applications
Fluid Jets
Nozzles
Vanes
Pipe Bends
EXAMPLE : Momentum Application
A 15 m/s jet of water (diameter 30 mm) is filling a tank. The tank has a
mass of 5 kg, and contains 20 liters of water as shown. The water temp
is 15 deg C.
Find:
‐ Force acting on the stop block.
‐ Force acting on the bottom of the tank
SOLUTION………….cont.
EXAMPLE:
Momentum Application-Vane
 A horizontal jet strikes a vane that is moving at a speed vv = 7 m/s.
Diameter of the jet is 6 cm. Speed of the fluid jet is 20 m/s, relative to a
fixed frame. What components of force are exerted on the vane by the
water in the x and y directions? Assume negligible friction between the
water and the vane.
SOLUTIONS
‫پره‬
SOLUTIONS cont……..
‫معادله برنولی‬
Restrictions on Bernoullis’ Equation
Valid only for incompressible fluids
No energy is added or removed by pumps, brakes,
valves, etc.
No heat transfer from or to liquid
No energy lost due to friction
Torricelli’s Theorem
 For a liquid flowing from a tank or
reservoir with constant fluid
elevation, the velocity through the
orifice is given by:
v2 
2 gh
h
where, h is the difference in
elevation between the orifice and
the top of the tank
Example: If h = 3.00 m, compute v2
Given : Right figure
Determine : Vp  ?
24
Solution :
3
2
(
10
m
)
4
2
A1  Ap  500 mm2

5

10
m
(1mm) 2
V1  V p  ?
cm 3 1min (1m)3
6
3
Q2  V2 A2  300

5

10
m
/s
2
3
min 60 s (10 cm)
Q1  Qleak  V1 A1  0.1Q2  5  10 7 m3 / s
dmsys 
 cv dV   ( iVi Ai ) out   (  jV j Aj )in  0
dt
t
i
j
dmsys
dt



t

cv
25
dV   ( iVi Ai ) out   (  jV j A j )in  0
i
j
[ A1l  needle ]  V1 A1  V2 A2  0
t
Since   const .
and
needle  0

l
( A1l )  V1 A1  V2 A2  A1  Q1  Q2  0
t
t
l
1
   Q1  Q2 
t
A1

l 1
1
7
6
3
2
V p    Q1  Q2  
5

10

5

10
m
/
s

1
.
1

10
m/s
4
2
t A
5  10 m
3
 2 m 10 mm 60 s
 1.1 10
 0.66 mm / min
s 1m 1 min

