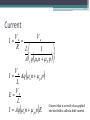Download Carrier Mobility

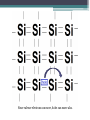
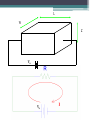
Carrier Motion - Electric Fields
ECE 2204
Movement of Electrons and Holes
• Nearly free electrons can easily move in a semiconductor
since they are not part of a chemical bond between atoms.
• Valence electrons are shared between atoms. It turns out
that a valence electron can also exchange places with
another valence electron that is being shared with a
different atom.
Since valence electrons can move, holes can move also.
Carrier Mobility and Velocity
• Mobility - the ease at which a carrier (electron
or hole) moves in a semiconductor
▫ Symbol: mn for electrons and mp for holes
• Drift velocity – the speed at which a carrier
moves in a crystal when an electric field is
present. The electric field is the force applied to
the carrier.
▫ For electrons: vd = mn E
▫ For holes:
v d = mp E
Carrier mobility
• The ease at which electrons and holes can move
depends on the semiconductor material.
Semiconductor
mn (cm2-V-1-s-1)
mp (cm2-V-1-s-1)
Si
1350
450
Ge
2000
2000
GaAs
8500
400
▫ Nearly free electrons in direct semiconductors are
faster than nearly free electrons in indirect
semiconductors. Extremely high speed electronic
devices are usually made from these materials.
Direction of Carrier Motion
• Suppose we consider a piece of intrinsic
semiconductor to be a resistor (which it is) and
attach a dc voltage source to it.
▫ Let say that the length of the semiconductor is L,
its width is W, and the height is Z.
▫ The magnitude of the voltage source is Va.
L
W
Z
Va
Va
Resistance
The equation for resistance that we used in ECE 2004 is shown below.
L
L
R
 
WZ
A
R is resistance in W.
 is resistivity with units of W-cm.
L is the distance that the current has to flow as it enters and leaves the
resistor.
WZ is the cross-sectional area A of the material.
Resistivity and Conductivity
• Fundamental material properties
1
1


q m n n  m p p  q m n  m p ni

1

Questions
• Since the resistance of the semiconductor
depends on its geometry
▫ What do you expect to happen to the resistance of
the Si bar if L increases?
▫ How about as either W and H increases?
Current
Va
Va
I

R

L 
1

A  q m n n  m p p  
Va
I
Aq m n n  m p p 
L
Va
E
L
Current that is a result of an applied
electric field is called a drift current.
I  Aq m n n  m p p E
Drift Currents
I
driftt
I
drift
n
A
I
drift
p
A
 Aqm n n  m p p E
J
drift
n
 qm n nE
J
drift
p
 qm p pE
Energy Diagram
e
eVa
EC
EF
EV
Slopes on the energy
diagram indicate that an
electric field is present at
that location.
h
e
h
Ip
Va
In
Questions
• Assume that the electron and hole mobilities are
constant.
▫ What happens to the resistance of the Si bar as the
temperature increases?
• Suppose there were bars of Si, Ge, and GaAs that
had exactly the same dimensions.
▫ At a particular temperature (say 300K), which bar
has the lowest resistance?