* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The First Law of Thermodynamics
Survey
Document related concepts
Transcript
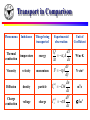
Physics I The First Law of Thermodynamics Prof. WAN, Xin [email protected] http://zimp.zju.edu.cn/~xinwan/ Heat Conduction Fourier heat conduction law Q dT t A t dx Remind you of Ohm’s law? Energy Transfer Through Two Slabs Kinetic Theory T Energy exchange across plane A 1 1 Q U R U L CV T 2 2 f 2 N V Al k B dT l dx 1 f P l T t lvth T 22T UL, NL UR, NR Q l l Q dT t A t dx f 1 ~ 2 dm m t for Air at Room Temperature From last lecture l 2.25 107 m v 500 m/s 5 1 f P 1 5 10 N/m t lvth 2.25 107 m 500m/s 22T 2 2 300K 0.047 W/(m K) A factor less than 2 larger than the measured value of 0.026. Not bad after so many crude approximations. Transport in Comparison Phenomena Imbalance Things being transported Thermal conduction temperature energy Viscosity velocity momentum Diffusion density particle Charge conduction voltage charge Experimental observation Q dT t A t dx dv F A dy dn (n) I x DA dx dV (e) I x A dx Unit of Coefficient W/m·K N·s/m2 m2/s W-1m-1 Internal Energy, Heat & Work Heat is defined as the transfer of energy across the boundary of a system due to a temperature difference between the system and its surroundings. Energy can also be transferred to or from the system by work. Internal energy is all the energy of a system that is associated with its microscopic components —atoms and molecules —when viewed from a reference frame at rest with respect to the object. Mechanical Equivalence of Heat The amount of energy transfer necessary to raise the temperature of 1 g of water from 14.5oC to 15.5oC. Specific Heat Note: Last time we defined molar specific heat. In physics, we also use specific heat per particle. Help Young Leonardo DiCaprio A cowboy fires a silver bullet with a mass of 2 g and with a muzzle speed of 200 m/s into the pine wall of a saloon. Assume that all the internal energy generated by the impact remains with the bullet. What is the temperature change of the bullet? Kinetic energy 1 2 1 2 mv 2 10 3 kg 200 m/s 40 J 2 2 convert to heat Q 40 J T 85 . 5 C 3 mc 2 10 kg 234 J/kg C Latent Heat in Phase Changes Latent Heat The latent heat of vaporization for a given substance is usually somewhat higher than the latent heat of fusion. Why? Work in Thermodynamic Processes Quasi-static assumption: the gas expands slowly enough to allow the system to remain essentially in thermal equilibrium at all times. Work done by the gas dW Fdy PAdy PdV Vf W PdV Vi Work in Thermodynamic Processes Work done by the gas dW Fdy PAdy PdV Vf W PdV Vi The work done by a gas in the expansion from an initial state to a final state is the area under the curve connecting the states in a PV diagram. Warning: Sign Convention Historically, people are interested in the amount of work done by the expansion of gas, say, to drive a steam engine. The common treatment is – Positive work: gas expands – Negative work: gas compressed In mechanics we use the opposite sign, unfortunately. But some books follow the same convention in thermal physics as in mechanics. Trust your common sense! Work Depends on the Path W ( a ) Pf (V f Vi ) W ( a ) W ( c ) W (b ) W (b) Pi (V f Vi ) The work done by a system depends on the initial, final, and intermediate states of the system. Isothermal Expansion • The gas does work on the piston W 0 • Energy is transferred slowly to the gas Q0 An energy reservoiris a source of energy that is considered to be so great that a finite transfer of energy from the reservoir does not change its temperature. Free Expansion • No heat or energy is transferred Q0 • The value of the work done is zero W 0 Energy transfer by heat, like work done, depends on the initial, final, and intermediate states of the system. The 1st Law of Thermodynamics Although Q and W both depend on the path, the quantity Q-W is independent of the path change. The change in the internal energy U of the system can be expressed as: U Q W The infinitesimal change: dU dQ PdV reminding you that it is path dependent Discussion on the 1st Law The 1st law is a statement of energy conservation (now with the internal energy included). The internal energy of an isolated system remains constant. In a cyclic process, U 0, Q W – The net work done by the system per cycle equals the area enclosed by the path representing the process on a PV diagram. Discussion on the 1st Law On a microscopic scale, no distinction exists between the result of heat and that of work. The internal energy function is therefore called a state function, whose value is determined by the state of the system. – In general, U U (T , V ) Digression on Multivariate Calculus If we take energy and volume as parameters, how comes heat is path dependent? dQ dU PdV In mathematical language, dU + pdV is an inexact differential. – In multivariate calculus, a differential is said to be exact (or perfect), as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q. Inexact Differential x Assume dg dx dy y ( 2,1) ( 2, 2) dx x dy 1 2 ln 2 ( 2,1) y (1,1) (1, 2) ( 2, 2) dx x dy ln 2 1 (1,2) y (1,1) dg dx dy Note: df x x y Integrating factor is an exact differential. f ( x, y) ln x ln y f 0 Ideal Gas Experiments found pV NkBT Kinetic theory found 2N 1 2 pV mv 3 2 1 2 3 mv k BT 2 2 Generalized equipartition theorem (can be proved based on statistical principles f U N k BT 2 f U CV NkB T fixed V 2 Isobaric & Isovolumetric Processes isobaric W P(V f Vi ) U CV T Q U W CV T PV PV Nk BT CV T Nk B T Q CP CV Nk B T fixed P CV f / 2NkB CP f 2 CV f Isobaric & Isovolumetric Processes isobaric W P(V f Vi ) U CV T Q U W CV T PV PV Nk BT CV T Nk B T Q CP CV Nk B T fixed P Molar specific heat: CP CV R Isobaric & Isovolumetric Processes isobaric W P(V f Vi ) U CV T Q U W CP T isovolumetric W 0 U CV T Q U CV T Isothermal Expansion Vf Vf Vi Vi W PdV Vf NkBT dV NkBT ln V Vi U 0 Q W Nk BT ln Vf Vi Adiabatic Expansion adiabatic dQ 0 CV dT dU PdV P Nk BT V CV dT Nk B dV T V TV CP C 1 NkB C V V 1 const or PV const (Adiabatic) Free Expansion U 0 Q W 0 Questions: • Is it possible to show the process on the PV diagram? • Is it reversible? Degrees of Freedom, Again f CV Nk B 2 f 2 CP Nk B 2 CP f f 2 CV f 3 5 7 1.67 1.4 1.28 Homework CHAP. 22 Exercises 11, 19, 21 (P540) 24, 25 (P541)