* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download MATH103
Functional decomposition wikipedia , lookup
Line (geometry) wikipedia , lookup
Big O notation wikipedia , lookup
Principia Mathematica wikipedia , lookup
Dirac delta function wikipedia , lookup
Continuous function wikipedia , lookup
Non-standard calculus wikipedia , lookup
History of the function concept wikipedia , lookup
Multiple integral wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Function (mathematics) wikipedia , lookup
MATH103
Mathematics for Business and
Economics - I
Chapter 2 – Functions and Graphs
2.1 Functions
The idea of a function is this: a correspondence between two
sets D and R such that to each element of the first set, D,
there corresponds one and only one element of the second
set, R.
The first set is called the domain, and the set of corresponding
elements in the second set is called the range.
Notation: if y is a function of x, we write
◦ y = f(x)
◦ Other common symbols for functions include but are not
limited to g, h, F, G
Function Evaluation
2
• Consider our function f ( x) x 2
• What does f (-3) mean?
Replace x with the value –3 and evaluate the
expression
f (3) (3)2 2
• The result is 7 . This means that the point (-3,7) is
on the graph of the function.
EXAMPLE 1
Evaluating a Function
Let g be the function defined by the equation
y = x2 – 6x + 8.
Evaluate each function value.
1
b. g 2
c. g
a. g 3
2
e. g x h
d. g a 2
Solution
a. g 3 32 6 3 8 1
b. g 2 2 6 2 8 24
2
EXAMPLE 1
Evaluating a Function
Solution continued
2
21
1 1
1
c. g 6 8
2 2
2
4
d. g a 2 a 2 6 a 2 8
2
a 2 4a 4 6a 12 8
a 2 2a
e. g x h x h 6 x h 8
2
x 2xh h 6x 6h 8
2
2
AGREEMENT ON DOMAIN
If the domain of a function that is defined
by an equation is not explicitly specified,
then we take the domain of the function to
be the largest set of real numbers that result
in real numbers as outputs.
Domain of a Function
• Consider f ( x) 3x 2
f (0) ?
f (0) 3(0) 2 2
which is not a real number.
• Question: for what values of x is the function defined?
• Answer: f ( x) 3x 2
is defined only when the radicand (3x-2) is equal to or greater
than zero. This implies that
x
2
3
Therefore, the domain of our function is the set of real numbers that are greater
than or equal to 2/3.
• Example1: Find the domain of the function
f ( x)
• Answer:
1
x4
2
x x 8 ,
[8, )
• Example : Find the domain of
1
f ( x)
3x 5
• In this case, the function is defined for all values of x
except where the denominator of the fraction is zero.
This means all real numbers x except 5/3.
EXAMPLE 3
Finding the Domain of a Function
Find the domain of each function.
1
a. f x
b. g x x
2
1 x
1
c. h x
d. P t 2t 1
x 1
Solution
a. f is not defined when the denominator is 0.
1 x2 0
x 1
Domain: {x|x ≠ –1 and x ≠ 1}
, 1 1,1 1,
EXAMPLE 3
Finding the Domain of a Function
Solution continued
b. g x x
The square root of a negative number is not a
real number and is excluded from the domain.
Domain: {x|x ≥ 0}, [0, ∞)
1
c. h x
x 1
The square root of a negative number is not a
real number and is excluded from the domain,
so x – 1 ≥ 0. However, the denominator ≠ 0.
EXAMPLE 3
Finding the Domain of a Function
Solution continued
So x – 1 > 0 so x > 1.
Domain: {x|x > 1}, or (1, ∞)
d. P t 2t 1
Any real number substituted for t yields a
unique real number.
Domain: {t|t is a real number}, or (–∞, ∞)
Example #2a (p.80)
• Find the domain of f(x) = x/(x2 –x – 2)
– The domain would be the set of all real numbers except
those values of x which set the denominator equal to zero
– These values are found by factoring
• (x2 –x – 2) = (x + 1)(x - 2)
• x = -1, 2
– So the domain is the set of all real numbers , except x =-1, 2
Equality of Functions
• Two functions, f and g are equal (f = g) if
– The domain of f is equal to the domain of g
– For every x in the domain of f and g, the values of
the two functions are the same; that is f(x) = g(x)
Example #1 (p. 79-80)
• Which of the following functions are equal
– f(x) = (x + 2)(x + 1)/(x – 1)
– g(x) = x + 2
– h(x) = x + 2
• Domains of g, h, the set of all real numbers
and are equal,
• but the domain of f is the set of all real
numbers except x = 1
1
2
A polynomial function of degree n is a function of the form
f x an x an1 x
n
n1
... a2 x a1 x a0 ,
2
where n is a nonnegative integer and the coefficients an, an–1, …, a2,
a1, a0 are real numbers with a ≠ 0.
3
4
2.3 Combinations of Functions
(i) Sum
f g x f x g x
(ii) Difference
f g x f x g x
(iii) Product
fg x f x g x
(iv) Quotient
f x
f
g x g x , g x 0.
(v)
EXAMPLE 1
Combining Functions
EXAMPLE 2
Combining Functions
f(x) = x2 , g(x) = 3x, find;
i. f(x) + g(x) = x2 + 3x
ii.
f(x).g(x) = 3x3
iii. f(x) – g(x) = x2 – 3x
iv. f(x)/g(x) = x2/3x = x/3
v.
cf(x) = cx2
EXAMPLE 3
Combining Functions
Let f x x 6x 8, and g x x 2.
Find each of the following functions.
2
a. f g x
b. f g x
c. fg x
f
d. x
g
Solution
a. f g x f x g x
x 6x 8 x 2
2
x 2 5x 6
EXAMPLE 3
Combining Functions
Solution continued
f x x 2 6x 8 and g x x 2
b. f g x f x g x
x 6x 8 x 2
2
x 2 7x 10
c. fg x x 2 6x 8 x 2
x 2x 6x 12x 8x 16
3
2
2
x 8x 20x 16
3
2
EXAMPLE 3
Combining Functions
Solution continued
f x x 2 6x 8 and g x x 2
f x
f
d. x
, g x 0
g
g x
x 6x 8
, x20
x2
x 2 x 4
, x2
x2
2
COMPOSITION OF FUNCTIONS
If f and g are two functions, the composition
of function f with function g is written as
f og and is defined by the equation
f og x f g x ,
where the domain of f og consists of those
values x in the domain of g for which g(x) is
in the domain of f.
COMPOSITION OF FUNCTIONS
EXAMPLE 1
Evaluating a Composite Function
3
f
x
x
and g x x 1.
Let
Find each of the following.
a. f og 1
b. g o f 1
c. f o f 1
Solution
d. g og 1
a. f og 1 f g 1
f 2
23
8
EXAMPLE 1
Evaluating a Composite Function
Solution continued
f x x 3 and g x x 1
b. g o f 1 g f 1
g 1 1 1 2
c. f o f 1 f f 1
f 1 1 1
3
d. g og 1 g g 1
g 0 0 1 1
EXAMPLE 2
Finding Composite Functions
2
f
x
2x
1
and
g
x
x
3.
Let
Find each composite function.
a. f og x
b. g o f x
Solution
a. f og x f g x
2 x
3 1
f x 3
2
2
2x 2 6 1
2x 2 5
c. f o f x
EXAMPLE 2
Finding Composite Functions
Solution continued
f x 2x 1 and g x x 2 3.
b. g o f x g f x
g 2x 1
2x 1 3 4x 4x 2
2
2
c. f o f x f f x
f 2x 1
2 2x 1 1 4x 3
EXAMPLE 3
Finding the Domain of a Composite Function
1
Let f x x 1 and g x .
x
a. Find f og 1.
b. Find g o f 1.
c. Find f og x and its domain.
d. Find g o f x and its domain.
Solution
a.
f og 1 f g 1
f 1 1 1 0
EXAMPLE 3
Finding the Domain of a Composite Function
1
f x x 1 and g x
x
b. g o f 1 g f 1
Solution continued
g 0 not defined
1 1
c. f og x f g x f 1
x x
Domain is (–∞, 0) U (0, ∞).
1
d. g o f x g f x g x 1
x 1
Domain is (–∞, –1) U (–1, ∞).
EXAMPLE 4
Let H x
Decomposing a Function
1
. Show that each of the
2x 1
following provides a decomposition of H(x).
2
a. Express H x as f g x ,
1
where f x
and g x 2x 2 1.
x
b. Express H x as f g x ,
1
where f x and g x 2x 2 1.
x
EXAMPLE 4
Decomposing a Function
Solution
a. f g x f 2x 2 1
1
2x 2 1
H x
b. f g x f
2x 1
2
1
2x 1
H x
2
An ordered pair of real numbers is a pair of
real numbers in which the order is specified,
and is written by enclosing a pair of numbers in
parentheses and separating them with a comma.
The ordered pair (a, b) has first component a
and second component b. Two ordered pairs
(x, y) and (a, b) are equal if and only if x = a
and y = b.
The sets of ordered pairs of real numbers are
identified with points on a plane called the
coordinate plane or the Cartesian plane.
Definitions
We begin with two coordinate lines, one
horizontal (x-axis) and one vertical (y-axis), that
intersect at their zero points. The point of
intersection of the x-axis and y-axis is called the
origin. The x-axis and y-axis are called
coordinate axes, and the plane formed by them
is sometimes called the xy-plane.
The axes divide the plane into four regions called
quadrants, which are numbered as shown in the
next slide. The points on the axes themselves do
not belong to any of the quadrants.
Definitions
The figure shows how each ordered pair (a, b)
of real numbers is associated with a unique
point in the plane P, and each point in the plane
is associated with a unique ordered pair of real
numbers. The first component, a, is called the
x-coordinate of P and the second component,
b, is called the y-coordinate of P, since we
have called our horizontal axis the x-axis and
our vertical axis the y-axis.
Definitions
The x-coordinate indicates the point’s distance to
the right of, left of, or on the y-axis. Similarly, the
y-coordinate of a point indicates its distance above,
below, or on the x-axis. The signs of the x- and ycoordinates are shown in the figure for each
quadrant. We refer to the point corresponding to
the ordered pair (a, b) as the graph of the ordered
pair (a, b) in the coordinate system. The notation
P(a, b) designates the point P in the coordinate
plane whose x-coordinate is a and whose
y-coordinate is b.
EXAMPLE 1
Graphing Points
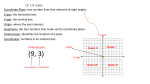
Graph the following points in the xy-plane:
A 3,1, B 2, 4 , C 3, 4 , D 2, 3, E 3, 0
Solution
A 3,1
3 units right, 1 unit up
B 2, 4 2 units left, 4 units up
C 3, 4 3 units left, 4 units down
D 2, 3 2 units right, 3 units down
E 3, 0
3 units left, 0 units up or down
EXAMPLE 1
Graphing Points
Solution continued
Copyright © 2007 Pearson Education, Inc. Publishing as
Pearson Addison-Wesley
Slide 2.1- 42
Definitions
The points where a graph intersects (crosses or touches) the
coordinate axes are of special interest in many problems.
Since all points on the x-axis have a y-coordinate of 0, any
point where a graph intersects the x-axis has the form (a, 0).
The number a is called an x-intercept of the graph. Similarly,
any point where a graph intersects the y-axis has the form (0,
b), and the number b is called a y-intercept of the graph.
PROCEDURE FOR FINDING THE INTERCEPTS OF A GRAPH
Step1
To find the x-intercepts of an equation, set y = 0 in
the equation and solve for x.
Step 2
To find the y-intercepts of an equation, set x = 0 in
the equation and solve for y.
EXAMPLE 1
Finding Intercepts
EXAMPLE 2
Finding Intercepts
Find the x- and y-intercepts of the graph of the
equation y = x2 – x – 2.
Solution
Step 1 To find the x-intercepts, set y = 0, solve
2
for x.
0 x x2
0 x 1x 2
x 1 0 or x 2 0
x 1 or
x2
The x-intercepts are –1 and 2.
EXAMPLE 2
Finding Intercepts
Solution continued
Step 2 To find the y-intercepts, set x = 0, solve
for y.
y 02 0 2
y 2
The y-intercept is –2.
The graph of the linear equation(line)
The following steps can be used to draw the graph of
a linear equation.
Step1 ) Select at least 2 values for x
Step2 ) Substitute them in the equation and find the
corresponding values for y
Step3 ) Plot the points on cartesian plane
Step4 ) Draw a straight line through the points.
X
-2
-1
0
1
y
-1
1
3
5
5
3
1
-2
-1
1
-1
x-intercept
y=0 0=2x+3
x= 2/3
(2/3 , 0) is x-intercept
y- intercept
x=0 y=2.0+3
y= 3
(0,3) y-intercept
y-intercept
x-intercept
3
-2
Step1
Step2
Step3
Step4
x-intercept
x-intercept
3/2
-2
5
y-intercept
-49/4
Vertex point
Step1
Step3
Step2
Step4
Step5
Step 4 : a 1 0, concave up
Ex : Sketch the Graph of y x 2 4 x 8
Solution :
step1: Vp 2, 4
b
4
b 2 4ac 16 4(1)(8) 16
2,
4
2a 2(1)
4a
4(1)
4
Step 2 : x intercept(s), y 0
x2 4 x 8 0
42 4(1)(8) 16 32 16 0 no x intercept(s)
this graph never cuts x-axis
Step3 : y intercept, x 0
y 8 (0, 8)
Step 4 : a 1 0, concave down
2
4
y-intercept
-8
Vertex point