* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download CommonGeometricTerms Lines
Line (geometry) wikipedia , lookup
Perceived visual angle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
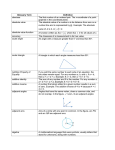
CommonGeometric Terms
Lines
90°
INTERSECTINGLINES
1. Two lines that cross
through a common
point.
PERPENDICULARLINES
2. Two lines that form a
90° angle.
TANGENTLINES
3. A line that touches a
geometric shape at one
point only.
'i
PARALLELLINES
4. Unes that are an equal
distan98 apart and when
extended willnever intersect.
Angles
-"
SYMBOL FOR
RIGHT ANGLE
\VERTEAA
90°
ANGLE
1. A figure fonned when
two straight lines meet
at a point. The point
where lines meet is
called the vertex.
I
~
.or
~LE
I
GREATER
THAN
RIGHTANGLE
2. An angle that measures
90°.
ACUTE ANGLE
3. An angle less than 90°.
OBTUSE ANGLE
4. An angle greater than
90°.
Triangles
II
I
I
~
EQUILATERAL TRIANGLE
RIGHT TRIANGLE
1. A triangle with all sides
2. A triangle that has two
perpendicular sides.
of equal length.
62
Industrial Communication
ISOSCELES TRIANGLE
3. A triangle that has two
sides the same length.
SCALENETRIANGLE
4. A triangle that has three
sides of unequal length.
TO Draw a Line P,rpendlcular to An.other LiRe:
a
0
1, Put a center point 0 on
the line where you wish
the perpel7ldicOrar line to
be. Swing an arc A of
any radius.
64
Industria,1
2. Use the intersection of
arc A and the line as
the new eerlter point.
Swing an arc B with the
radius 'I!arger than the
radius of arc A.
Communication
3~U~et~e oPPOsiteside
of arc A as the center
point. Swing an ar,;eC
with the same rattius as
arc B.
A
0
4. Draw a line from the
intersection 0,1Band C
to the center point
O.
This line is perpendicular
to the first line.
eta
~1'!(orDiv;dea
LiDS into TwoEoualP.rtsJ;
A
.,
~,:tre
compass to a
more than one"1ehgthof the
2. Swing.arc A with the
corhpasscentered on
one end of the line.
3. Swingarc 8 with the
same radius as A from
theo1ber end of the line.
4. Draw a iinefrom. the
point where arcs A and
B intersi8Cton either
side of the line. This
new line bisects the
original line.
Ceo'metricConsitructian
63
\
-roRounda 90 Degree,Cornier:
..
..
'RADIUS
OF
OOrRNER
1, Swingan arc A that
RADIUS
OF
CORNER
RAD1US
OF
GORNiER
has tile same
2. Swingarcs Band C usIng the
radius as the round comer to,be
added~
same radius as arc A..The
center points for Band Care
the points where' arc A
ifltersects with the edges.
--
J
-.
.
3. Use the intersection point o,f
arcs Band C as the cel"lter
point.Swing the finalarc at the
same radius as A, 8, and C to
roundthe corner,
tt:J81sec\taniAI111eCor
Dfvidean Angle Into J:Cll.lal
, Angles}:
c
B
.
c
~J~
~
\A
1, Using the vertex of the angle
as the center point, swing an
arc A at any convenient radius,
3. Drawa line from the
2. Swing arcs 8 and C as !?hown. Arcs
Band C shouldhave the same radius
and should be large enough to
intersect.
intersection of arcs 8
and C to the vertex of
the angle. This line
bisects the angle.
J
!
'o>Qe,.,_trUQtan
'I€luj/atfJ,at
"iangle:
('
t
AB{j7
1. Draw a Unethe length
that you VIIantthe sides
of the triangle to be.
2. Centerthe compassat
one end of the Une.
Swing arc A with a
radiusthe same ength
3.. Centerthe compassat
the opposite end of the
line. Swingarc B with
the same radius.
l
tj
"'."
B
"A
4. Drawstraightlines from
the ends of the line to
the Intersection point of
arcs A and B.
as the line"
,
GeometricConstructIon 65