Download Work, Energy, and Momentum

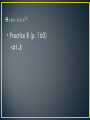
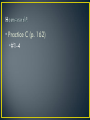
Physics 1-2
Mr. Chumbley
Chapters 5 and 6
Chapter 5, Section 1
• In everyday usage, work is generally referred to as anything
that requires some sort of physical or mental effort
• In physics, work is a specific, measurable quantity
• Work is done on an object when a force causes a displacement
of the object
• Work is the product of the component of a force along the
direction of displacement and the magnitude of the
displacement
𝑊 = 𝐹𝑑
• Taking the SI units of force and displace net, the unit of work
could be N·m
• The N·m is condensed and called the joule (J)
How much work is done on a vacuum cleaner pulled 3.0 m by a
force of 50.0 N?
Given:
F = 50.0 N
d = 3.0 m
𝑊 = 𝐹𝑑
𝑊 = 50.0 N 3.0 m
𝑊 = 150 J
Unknown:
W=?
• Practice A (p. 156)
•#1-4, no angles
1. 1.50 × 107 J
2. 7.0 × 102 J
3. 1.8 × 103 J
4. 1.1 m
Chapter 5, Section 2
• Energy can be defined as the ability to do work
• This means that when work is done on an object, the amount of
energy the object has increases
• Also, if an object does work on another object, or on the
surrounding environment, then its energy decreases
• Objects in motion have a specific type of energy
• Kinetic energy is the energy of an object that is due to the object’s
motion
• If we apply Newton’s 2nd Law to the mathematical definition of work,
the change in kinetic energy due to work can be found
• In a general sense, the kinetic energy of an object is equal to half the
product of the object’s mass and its speed squared
1
𝐾𝐸 = 𝑚𝑣 2
2
A 7.00 kg bowling ball moves at 3.00 m/s. How fast must a 2.45g
ping-pong ball move in order to have the same kinetic energy as the
bowling ball?
𝐾𝐸bb =
1
𝑚𝑣2
2
Given:
mbb = 7.00 kg
v = 3.00 m/s 𝐾𝐸𝑏𝑏 = 1 7.00 kg 3.00 m/s
2
mpp = 2.45 g
Unknown:
KEbb = ?
vpp = ?
𝐾𝐸bb = 31.5 J
1
𝐾𝐸bb = (𝑚pp)(𝑣pp)2
2
2
𝑣pp =
2𝐾𝐸bb
𝑚pp
𝑣pp =
2(31.5 J)
(0.00245 𝑘𝑔)
𝑣pp = 1.60 × 102 m/s
• Practice B (p. 160)
•#1-5
• When work is done on object to change its motion, there is a
specific relationship between the work done and the change in
kinetic energy
• The work-kinetic energy theorem states that the net work done
by all the forces acting on an object is equal to the change in
the object’s kinetic energy
𝑊𝑛𝑒𝑡 = ∆𝐾𝐸
𝑊𝑛𝑒𝑡
1
1
2
= 𝑚𝑣𝑓 − 𝑚𝑣𝑖2
2
2
On a frozen pond, a person kicks a 10.0 kg sled, giving it an initial speed of 2.2
m/s. How far does the sled move if the coefficient of friction between the sled and
the ice is 0.10?
𝑊𝑛𝑒𝑡 = 𝐹𝑛𝑒𝑡 ∆𝑥
Given:
m = 10.0 kg
vi = 2.2 m/s
vf = 0 m/s
μk = 0.10
Unknown:
Δx = ?
𝐹𝑛𝑒𝑡 = 𝐹𝑓 = 𝜇𝑘 𝐹𝑁 = −𝜇𝑘 𝑚𝑔
𝑊𝑛𝑒𝑡
𝑣𝑖2
∆𝑥 = −
2𝜇𝑘 𝑔
1
1
= ∆𝐾𝐸 = 𝑚𝑣𝑓2 − 𝑚𝑣𝑖2
∆𝑥 = −
2
2
1
1
2
𝐹𝑛𝑒𝑡 ∆𝑥 = 𝑚𝑣𝑓 − 𝑚𝑣𝑖2
2
2
1
𝜇𝑘 𝑚𝑔∆𝑥 = − 𝑚𝑣𝑖2
2
m 2
2.2
s
m
2 0.10 −9.81 2
s
∆𝑥 = 2.5 m
• Practice C (p. 162)
•#1-4
• Even when objects are not moving, they possess some capability
to gain kinetic energy
• Potential energy is the energy associated with an object due to
the position, shape, or condition of the object
• Two major types of potential energy in mechanics
• Gravitational Potential Energy
• Elastic Potential Energy
• When looking at falling objects, it is easy to identify the kinetic
energy that is being gained, but that energy needs to come
from somewhere
• Gravitational potential energy is the potential energy stored in
the gravitational fields of interacting bodies
• Gravitational potential energy (PEg) is equal to the product of
the mass of an object, the acceleration due to gravity, and the
height of the object
𝑃𝐸𝑔 = 𝑚𝑔ℎ
A 5.8 kg box is placed on a 2.5 m high shelf. What is the potential energy of the
box as it sits on the shelf?
Given:
m = 5.8 kg
g = 9.81m/s2
h = 2.5 m
Unknown:
PEg= ?
𝑃𝐸𝑔 = 𝑚𝑔ℎ
𝑃𝐸𝑔 = 5.8 kg 9.81m/s2 (2.5 m)
𝑃𝐸𝑔 = 140 J
Chapter 5, Section 3
• When looking at changes in energy in a system, it is necessary
to look at all of the different types of energy
• However, to simplify the total energy, certain types can be
isolated
• Total mechanical energy (ΣME) is the sum of the kinetic and
potential energies
Σ𝑀𝐸 = 𝐾𝐸 + Σ𝑃𝐸
• One of the most fundamental scientific concepts is the
conservation of energy
• Looking at simply mechanical energy, conservation of energy
still generally applies
Σ𝑀𝐸𝑖 = Σ𝑀𝐸𝑓
• This situation only applies if work is not done on an object,
primarily from friction
Starting from rest, a 25.0 kg child zooms down a frictionless slide from an initial
height of 3.00 m. What is her speed at the bottom of the slide?
Given:
m = 25.0 kg
vi = 0 m/s
hi = 3.00 m
hf = 0 m
Unknown:
vf = ?
• Practice E (p. 171)
•#1-3
Chapter 5, Section 4
• So far, we have only looked at the amount of energy gained by
performing work on an object
• The rate at which work is done is also a valuable quantity
• Power is a quantity that measures the rate at which work is done or
energy is transformed
𝑊
𝑃=
∆𝑡
𝑃 = 𝐹𝑣
• The SI unit of power is the watt (W), which is defines as one
joule per second
• Another common unit of power that is horsepower, which is
equal to 746 watts
A 193 kg curtain needs to be raised 7.5 m, at a constant speed, in as close to
5.0 s as possible. The power ratings for three separate motors are listed as 1.0
kW, 3.5 kW, and 5.5 kW. Which motor is best for the job?
Given:
m = 193 kg
Δt = 5.0 s
Δx = 7.5 m
Unknown:
P= ?
𝑊
𝑃=
∆𝑡
𝑊 𝐹∆𝑥 𝑚𝑔∆𝑥
𝑃=
=
=
∆𝑡
∆𝑡
∆𝑡
(193 kg)(9.81 m/s2)(7.5 m)
𝑃=
(5.00 s)
𝑃 = 2839 𝑊 = 2.8 kW
• Practice F (p. 174)
•#1-5
Chapter 6, Section 1
• Previously, we looked at forces being applied over a distance
• Look forces being applied over an amount time also results in a
valuable quantity
• Momentum is a physical quantity of an object in motion defined
by the product of the mass and the velocity of the object
𝐩 = 𝑚𝐯
• There is no specific SI unit of momentum, it is simply the
combination of the units of mass and velocity: kgm/s
• Momentum is also a vector quantity, so inclusion of direction is
needed
A 2250 kg pickup truck has a velocity of 25 m/s to the east. What is the
momentum of the truck?
Given:
m = 2250 kg
v = 25 m/s
𝐩 = 𝑚𝐯
𝐩 = (2250 kg)(25 m/s)
Unknown:
p= ?
𝒑 = 5.6 × 104 kgm/s
• Practice 6A (p. 191)
•#1-3
• Changes in momentum result from forces being applied to
object
• Identifying the connection between forces is fairly simple
• Mathematically, it is also possible to derive a relationship
between force and momentum
• Impulse is a quantity in physics that is used to describe a force
applied on an object during a given time interval,
• Impulse is defined as the product of the force and the time over which
the force acts on the object
• The impulse-momentum theorem states that the impulse acting an
object is equal to its change in momentum
𝐅∆𝑡 = ∆𝐩
𝐅∆𝑡 = ∆𝐩 = 𝑚∆𝐯 = 𝑚v𝒇 − 𝑚v𝒊
A 1400kg car moving westward with a velocity of 15 m/s collides with a utility
pole and is brought to rest in 0.30 s. Find the force exerted on the car durng
the collision.
Given:
m = 1400 kg
vi = 15 m/s west
vf = 0 m/s
Δt = 0.30 s
Unknown:
F= ?
𝐅∆𝑡 = 𝑚v𝒇 − 𝑚v𝒊
𝑚v𝒇 − 𝑚v𝒊
𝐅=
∆𝑡
(1400 kg)(o m s − 15 m s)
𝐅=
(0.30 s)
𝐅 = 𝟕. 𝟎 × 𝟏𝟎𝟒 𝐍 𝐞𝐚𝐬𝐭
• Practice 6B (p. 193)
•#1-4
Chapter 6, Section 2
• Similar to conservation of mechanical energy, the changes that occur
in the motion of objects can be described using conservation of
momentum
• When objects interact, the total momentum of the initial conditions is
equal to the total momentum of the final conditions
𝐩𝑖 = 𝐩𝑓
• The law of conservation of momentum states that the total momentum
of all objects interacting with one another remains constant regardless
of the nature of forces between the objects
𝑚1 𝑣1𝑖 + 𝑚2 𝑣2𝑖 = 𝑚1 𝑣1𝑓 + 𝑚2 𝑣2𝑓
• Conservation of momentum comes from Newton’s 3rd Law
• Conservation of momentum helps describe specific situations:
• Collisions with stationary objects
• Collisions of moving objects
• Objects pushing away from each other
A 76 kg boater, initially at rest in a stationary 45 kg boat, steps out of the
boat and onto a dock. If the boater moves out of the boat with a velocity of
2.5 m/s to the right, what is the final velocity of the boat?
Given:
m1 = 76 kg
v1i = 0 m/s
m2 = 45 kg
v2i = 0 m/s
v1f = 2.5 m/s right
Unknown:
v2f = ?
𝑚1 𝑣1𝑖 + 𝑚2 𝑣2𝑖 = 𝑚1 𝑣1𝑓 + 𝑚2 𝑣2𝑓
0 = 𝑚1 𝑣1𝑓 + 𝑚2 𝑣2𝑓
𝑚2 𝑣2𝑓 = −𝑚1 𝑣1𝑓
𝑣2𝑓
𝑣2𝑓
𝑚1 𝑣1𝑓
=−
𝑚2
(76 kg)(2.5 m/s)
=−
(45 kg)
𝑣2𝑓 = −4.2 m s = 4.2 m s left
• Practice 6D (p. 201)
•#1-4