Download Theory of Massive Star Formation

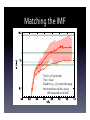
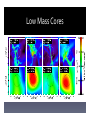
Theory of Massive Star Formation Mark Krumholz (UC Santa Cruz) Collaborators: Chris McKee, Richard Klein (UC Berkeley) Stella Offner, Kaitlin Kratter (CfA) Andrew Cunningham, John Bolstad (LLNL) Chris Matzner, Emmanuel Jacquet (Toronto / CITA) Andi Burkert (Munich) Circumstellar Dynamics at High Resolution, Foz de Iguaçu, Brazil March 1, 2012 Overview •  Introduction and observations •  Massive star formation models –  Fragmentation –  Disks and binarity –  The radiation pressure problem •  Summary The Observed IMF IMF properties: •  Peak at ~0.1 – 1 M"
•  Powerlaw tail (slope ~
−2.3) at high mass, up to 120 – 300 M •  (Nearly) universal − very limited evidence for weak variation IMF in the ONC (black), M35 (blue), Pleiades (green), field (red) (Kroupa 2002) Binarity Higher mass •  Most low mass stars are single •  Most massive stars are members of binary (or higher multiple) systems •  The companions to massive stars are also Multiple system fraction versus stellar mass in three different regions (Brown 2001) usually massive (Sana+ 2008) Star‐Forming Clouds and Cores Pipe nebula with cores circled (Alves+ 2007) The Core Mass Function •  CMF slope matches the IMF slope •  Seen in many regions •  Suggests IMF set by gas fragmentation and universal physics Core mass function in the Serpens, Perseus, & Ophiuchus clouds (Enoch+ 2008) Massive Cores Within these clouds we see centrally concentrated gas cores the right mass and size to be the progenitors of massive stars: M ~ 100 M, R < 0.1 pc, Σ ~ 1 g cm‐2 Core in IRDC 18223‐3 in mid‐IR (Spitzer, color) and mm (Plateau de Bure Interferometer, contours), (Beuther+ 2005) Caveat: fragmentation at unresolved scales Assembling the tail of the IMF Problem 1: Fragmentation •  Fragmentation scale is MJ ~ cs3 / G3/2 ρ1/2 ~ 1 M •  Why do some objects run away to ~100 MJ? Hydrodynamic simulation of the fragmentation of a massive core (Dobbs et al. 2005) Accretion Luminosity •  Accretion can produce > 100 L even for 0.1 M stars •  Accretion luminosity dominates energetics in star‐forming regions Temperature vs. radius before (red) and after (blue) star formation begins in a 50 M, 1 g cm‐2 core (Krumholz 2006) Basic Equations Mass conservation Gas momentum Gas energy Radiation energy Radiation momentum Radiation 4‐
force density Approximate Equations •  Non‐relativistic: work to 1st order in β •  Thermal radiation field: since τ >> 1 spectrum is thermal, integrate over ν •  Flux‐limited diffusion: since τ >> 1, flux F ∝ ‐∇E •  Build these approximations into the ORION adaptive mesh refinement code (Krumholz+ 2007), which also includes gravity and protostellar evolution Simulation of a Massive Core Movie 1  
 
Column density from simulation of a core with M = 100 M, r = 0.1 pc, σ = 1.7 km s–1 (Krumholz+ 2007) Left: whole core; right: central (2000 AU)2 Massive Cores Fragment Weakly •  With RT: few stars, most mass goes onto single largest star •  Without RT: many stars, stellar collisions, disk less massive •  Conclusion: radiation Column density with (upper) and without (lower) RT, for identical times and initial conditions inhibits fragmentation Massive Stars in a Cluster (Krumholz+ 2012, in prep)
Movie 2 Cloud embedded in a larger, turbulent medium; simulation includes protostellar outflows Matching the IMF Thick = 50th percentile Thin = mean Shaded = 25 – 75th percentile range Horizontal lines: da Rio+ (2012) IMF measured in the ONC Massive Cores Low Mass Cores Problem 2: Massive Binaries •  Radiative heating seems to suppress fragmentation into many stars •  Can we still explain the high fraction of massive stars that are binaries, and why those companions are also massive? Binaries from Cluster Simulation Binary Properties Massive Disk Properties •  Mdisk / M* ≈ 0.2 – 0.5, rdisk ~ 1000 AU •  Global GI creates strong spiral pattern •  Spiral waves drive rapid accretion; αeff ~ 1 •  Disks reach Q ~ 1, form stellar fragments Surface density (upper) and Toomre Q (lower); striping is from projection Understanding Massive Disks (Kratter+ 2006, 2008) •  Accretion rate onto star + disk is ~ σ3 / G ~ 10–3 M / yr in a massive core •  Max mass transfer rate through a stable disk (α < 1, Q > 1) is ~ cs3 / G ~ 5 x 10–5 M / yr at T = 100 K •  Core accretes faster than stable disk can process ⇒ massive, unstable disks Gravitational Instability in Disks (Kratter+ 2010; Krumholz & Burkert 2010)
Movie 3 Simulation shows growth of instability in rapidly‐fed disk, leading to fragmentation, and inward migration of fragments Searching For Companions •  Prediction: O stars should have GKM companions at separations of ~100 – 1000 AU •  These may be observable using coronagraphs or interferometers (e.g. GPI, VLTI, Project 1640) The Radiation Pressure Problem •  Dust absorbs UV & visible, re‐
radiates IR frad
fgrav
κL
=
4πr2 c
GM
= 2
r
•  frad > fgrav for (L/M) > 2500 •  Stars exceed this at ~20 M (Larson & Starrfield 1971; Wolfire & Cassinelli 1987)"
⇒  Massive stars exceed the dust Eddington limit while forming Simulations of Radiation Pressure (Krumholz+ 2009)
Movie 4 Radiation RT Instability Accretion occurs through radiation Rayleigh‐Taylor instability (Jacquet & Krumholz 2011) Simulations with Outflows (Krumholz+ 2005; Cunningham+ 2011)
Movie 5 Summary •  The fragmentation problem is solved by radiative feedback •  Binarity of massive stars is explained by a combination of n‐body dynamics and gravitational instability in disks •  The radiation pressure problem is solved by beaming