Download Chapter 7: Mechano-Acoustical Transformations

HANDBOOK OF THE SENSES
Audition Volume
Chapter 7: Mechano-Acoustical Transformations
Sunil Puria1,2 and Charles R. Steele1
1
Stanford University, Mechanical Engineering Department, Mechanics and
Computation Division, 496 Lomita Mall, Durand Building, Room 206, Stanford, CA
94305
2
Department of Otolaryngology-Head and Neck Surgery, 801 Welch Road,
Stanford, CA 94304
1
1. KEYWORDS
2. BIOMECHANICS, OTOBIOMECHANICS, COCHLEA,
COLLAGEN FIBERS, EXTERNAL EAR, IMPEDANCE, INNER
HAIR CELLS, LEVERS, MATHEMATICAL MODELS,
MICROCT, MIDDLE EAR, ORGAN OF CORTI, OUTER HAIR
CELLS, PRESSURE, TYMPANIC MEMBRANE, VIBRATION
2
I. Outline
In this chapter we examine the underlying biophysics of acoustical and mechanical
transformations of sound by the sub components of the ear. The sub components include
the pinna, the ear canal, the middle ear, the cochlear fluid hydrodynamics and the organ
of Corti. Physiological measurements and the deduced general biophysics that can be
applied to the input and output transformations by the different sub components of the ear
are presented.
II. Abstract
The mammalian auditory periphery is a complex system, many components of which
are biomechanical. This complexity increases sensitivity, dynamic range, frequency
range, frequency resolution, and sound localization ability. These must be achieved
within the constraints of available biomaterials, biophysics and anatomical space in the
organism. In this chapter, the focus is on the basic mechanical principles discovered for
the various steps in the process of transforming the input acoustic sound pressure into the
correct stimulation of mechano-receptor cells. The interplay between theory and
measurements is emphasized.
III. Main Body
A. Introduction
The auditory periphery of mammals is one of the most remarkable examples of a
biomechanical system. It is highly evolved with tremendous mechanical complexity.
What is the reason for such complexity? Why can’t hair cells tuned to various frequencies
just sit on the outside and detect motion due to sound? Clearly, the complexity serves the
animal by providing greater functionality. This can be appreciated by looking at simpler
auditory systems.
One of the simplest hearing organs is that of the fly (Drosophila melanogaster), which
has a tiny feather-like arista that produces a twisting force directly exerted by sound. This
sound receiver mechanically oscillates to activate the Johnston’s organ auditory receptors
with a moderately damped resonance at about 430 Hz (Gopfert and Robert 2001). The
level required to elicit a response, due to wing-generated auditory cues involved in
courtship, are in the 70 to 100 dB SPL range (Eberl et al. 1997). An example of a simpler
anatomy with more complex function than that of the fly is the Müller’s organ of the
locust. This invertebrate is capable of discriminating sounds at broadly tuned frequencies
of approximately 3.5-5, 8, 12 and 19 kHz corresponding to the four mechanotransduction
receptors attached to the tympanic membrane (Michelsen 1966). The best threshold for
the receptor cells is about 40 dB SPL. The resonances of the tympanic membrane and
attached organs provide the greater number of frequency channels than the fly (Windmill
3
et al. 2005). Amphibians evolved to have a basilar papilla with a few hundred receptor
cells in a fluid medium. Other amphibians, birds and mammals have many thousands of
hair cells. Other such examples, where structure that is more complex leads to greater
hearing capability, are found in some of the other chapters in this volume.
The peripheral part of the auditory system comprising of the external ear, middle ear
and the inner ear systematically transform and transduce environmental sounds to neural
impulses in the auditory nerve. The precise biophysical mechanisms relating the input
variables to the output variables of some of the subsystems are still being debated.
However, there is general agreement that these transformations lead to improved
functionality. Five of the most important functional considerations are described below.
1. Sensitivity. The human ear is most sensitive to a range of sounds from the
loudest at about 120 dB SPL to the softest at about –3 dB SPL. At its most
sensitive frequency near 4 kHz, the displacement at the tympanic membrane is
less than 1/10th the diameter of a hydrogen atom. At this threshold, the amount
of work that is done at the eardrumi is 3 x 10-18 J. In comparison, the amount
of work done for the perception of light at the retinaii is 4x10-18 J, which is
close to the calculated value at the threshold of hearing. This suggests that at
its limits, the two sensory modalities have comparable thresholds.
2. Dynamic range. The dynamic range of psychophysical hearing in humans is
about 120 dB SPL corresponding to environmental sounds and vocalized
sounds. However, the neurons of the auditory nerve have a dynamic range that
is typically less than 60 dB SPL. The organ of Corti mechanics must facilitate
this dynamic range mismatch problem.
3. Frequency range. Hearing has about 8.5-octave frequency range in human and
in some other mammals this range can be as wide as 11.5-octaves (ferrets). To
handle this processing mechanically, the sensory receptors should have
physical variations on a similar scale. However, the large range is achieved
over an extraordinarily small space in comparison to the wavelengths of
sound.
4. Frequency resolution. One of the most important functions of the cochlea is
the tonotopic organization, which maps different input frequencies to its
characteristic place in the cochlea. Like a Fourier frequency analyzer, each
characteristic place has narrow frequency resolution, which provides greater
sensitivity to narrow-band signals by reducing bandwidth and thus input noise
at the individual mechano-receptor hair cells and thus the auditory nerve.
5. Sound localization. The physical characteristics of the pinna and head diffract
sound in a spatially dependent manner. The diffraction pattern provides
important cues that allow the more central mechanisms to localize, segregate
and stream different sources of sound.
In this chapter, we follow the chain of acousto-mechanical transformations of sound
from the pinna to modulation of tension in inner hair cell tip links which is the final
mechanical output variable of the cochlea from our vantage point. The tension in the tip
links opens ion channels in the stereocilia, which then starts a chain of biochemical
events that leads to the firing of the auditory neurons. We designate the output of a given
4
sub system a proximate variable. The chain of proximate variables leads to the ultimate
output variable, the tip-link tension in hair cells. Input variables are sound pressure level,
morphometry of anatomical structures, and mechanical properties of those structures.
Biomechanical processes combined with the input variables lead to the proximate
variables, which are physiologically measurable.
B. Theories of sound transmission in the ear
Starting with Helmholtz, mathematical models have played a key role in improving our
understanding of the underlying biomechanical processes of the auditory periphery. In
comparison to using natural languages to describe the observed phenomena,
mathematical formulations have advantages and disadvantages. The advantages include a
methodology for the possibility to describe compactly a correspondence to reality. The
disadvantages are that the description may be incomplete or its validity difficult to test. A
mathematical model is also often a statement of a scientific theory that captures the
essence of the current state of the empirical observations. The power of a specific model
is its ability to evolve as more facts become available and to be able to predict facts not
yet observed. Thus the interplay between theory and experiments allows one to test
different hypotheses and generate new hypotheses.
In this chapter we provide a foundation for physiological measurements in the form of
mathematical models. Below we present some common principles, found all through the
auditory periphery, to transform the input variables to the ultimate output variable of hair
cell tip link tension. Several general concepts are presented. These include how levers are
formed, how Newton’s laws apply not only to celestial mechanics as originally
formulated but also in otobiomechanics, how sound transmission through different
materials is described by transmission line formulations, and how modes of vibrations
arise in structures. A combination of these principles is used to understand how the ear
improves sensitivity, frequency range, frequency resolution, dynamic range, and sound
localization within the constraints of biological materials and anatomic space.
1. Mechanical and acoustic levers
One of the simplest transformations of energy is achieved with a simple mechanical
lever. There are numerous places in the auditory periphery where levers produce force
and velocity transformations through anatomical changes in lengths and areas. These
transformations take place in the context of improving sound transmission at the
interfaces of different anatomical structures where there is a change in the impedance. An
example of a change in impedance is the low impedance of air to the high impedance of
the fluid filled cochlea. Examples of the lever action at work include an increase in sound
pressure due to a decrease in area of the concha of the pinna to the ear canal, increase in
pressure from the decrease in surface area from the tympanic membrane to the stapes
footplate, increase in force due to the lever ratio in the ossicular chain, increase in volume
velocity from the stapes footplate to the basilar membrane due to a decrease in surface
area, and transformation of the basilar membrane displacement to hair cell stereocillia tip
link tension due to relative shearing motion between the reticular lamina and the tectorial
membrane.
5
2. Newton’s second law of motion
A key principle in describing dynamic transformation of forces in mechanical systems
to accelerations is the well-celebrated Newton’s second law of motion elegantly written
as
F = ma ,
(Eq. 1)
which states that a force F acted upon a mass, results in acceleration a. Newton’s
second law, transformed to the frequency domain, is:
"
R
K
F(! ) = $ M +
+
$
j!
j!
#
( )
%
' a(! ) .
2
'
&
(Eq. 2)
Here the sinusoidal force F ( w) , with radian frequency ! , acts upon an object
described by the variables in the square bracket. This object has now been generalized to
include mass M, resistance R, and stiffness K. An alternative form of Eq. (2) in terms of
particle velocity v(! ) is:
#
K &
F(! ) = % j! " M + R +
" v(! ) ,
j! ('
$
(Eq. 3)
where the term in the square bracket is the mechanical impedance Z m . Sound
pressure P(! ) , measured with a microphone, is defined as the force per unit area A.
Thus, Eq. (3) can be rewritten for acoustics as
#
K &
P(! ) = % j! " M a + Ra + a ( "V (! )
j! '
$
(Eq. 4)
The term in the square bracket is now the acoustic impedance Z a , which for
uniform properties is the mechanical impedance Z m divided by A2, and V (! ) = v(! ) A is
the volume velocity.
One thing to keep in mind is that impedance concepts are limited to linear steady state
analyses. Despite this limitation, Eqs. (3) and (4) play a prominent role in helping us
understand transformations of forces and pressures to velocities and volume velocities
throughout the ear. It is clear from these equations that the velocity of any structure is
proportional to the applied force but inversely proportional to the impedance due to its
mass (M), damping (R) and stiffness (K). At resonance the velocity reaches a maximum
because the impeding effect of mass is cancelled by the impeding effect of stiffness. One
of the challenges in efficient sound transmission to the hair cell detectors is in minimizing
the impeding effect of fluid damping and stiffness and mass of structures.
3. Transmission lines
Many problems in sound and vibration are described by the wave equation that results
from Newton’s laws of motion. The one-dimensional (1-D) version of the wave equation
6
was formulated by d’Alembert in 1747 for the vibrating string. It did not take Euler very
long (1759) to formulate the first derivation of the wave equation for sound transmission
in one dimension and later in three dimensions (3-D). The wave equation has stood the
test of time as is evident by its use in disciplines that include electromagnetic theory,
transverse waves in stretched membranes, blood vessels, and electromagnetic
transmission lines. Because it was used so extensively in telephone communication and
power line transmission problems, the 1-D wave equation is also known as the
transmission line equation. In these equations the properties of the transmission system
are assumed to be constant along the direction of propagation. A special form of the wave
equation exists when a property along the propagation direction varies exponentially. As
reviewed by Eisner (1967), these equations were originally formulated by Lord Rayleigh
and are now known as Webster’s horn equation.
Subsequent sections will show that the transmission line formulation can be used to
describe ear canal acoustics, the coupling between the canal and tympanic membrane,
wave propagation in the cochlea, and transverse motion on the basilar membrane. The
series of transmission lines that are sequentially coupled may improve frequency
bandwidth while maintaining sensitivity of the proximate variables.
4. Modes of vibration
Anatomical structures and membranes have various modes of vibration with peak
responses at modal frequencies due to resonance. These modes of vibrations are not very
different from modes of vibrations in the strings of violins, guitars and pianos where the
ends of the strings are fixed are both ends. The resonant frequency is directly
proportional to the string tension and density but inversely proportional to its length.
More complicated modes of vibrations are found in membranes and plates. In the ear,
examples where resonances are a characteristic feature include the pinna and ear canal,
tympanic membrane, ossicles, the basilar membrane, organ of Corti, and hair cell
stereocilia. Despite the presence of structural resonances in many of the proximate
variables, the overall sensitivity of hearing varies smoothly with frequency and does not
exhibit sudden changesiii. Understanding this dichotomy has been challenging.
5. The input and output variables
Which input variable, at the ear-canal entrance determines sensitivity? Which output
variable characterizes changes in tension of the inner-hair-cell stereocilia? Possible
candidates for the input variable are pressure measured with a microphone, volumevelocity (acceleration and displacement), power, or transmittance and reflectance. Since
these variables are interrelated, it is difficult to truly separate the effects of one variable
from another. However, the use of pressure has some advantages.
Dallos (1973) showed that there is good agreement between hearing sensitivity
measured behaviorally and the eardrum-to-cochlear pressure transfer function, also called
the middle ear pressure gain resulting from ossicular coupling. It appears that the
combined properties of the middle ear and its cochlear load are the dominant
determinants of the animal’s measured behavioral sensitivity. This has been directly
measured in cat (Nedzelnitsky 1980), guinea pig (Dancer and Franke 1979; 1980;
Magnan et al. 1997), gerbil (Olson 1998) and human (Puria et al. 1997; Aibara et al.
2001; Puria 2003). In agreement with Dallos (1973), Puria et al (1997) show that there is
7
good correlation between the human middle ear pressure gain and behavioral threshold.
This suggests that an important proximate variable, at least at the base of cochlea, is fluid
pressure in the vestibuleiv.
In the organ of Corti it is well accepted that tension in the tip links is the ultimate
mechanical variable for the mechano-electric transduction (Corey and Hudspeth 1983;
Howard and Hudspeth 1988). This tension opens ion channels and initiates the flow of
ions through the stereocilia bundle resulting in depolarization of the hair cell body which
results in firing of the auditory nerve.
In the sections that follow we generally follow the path taken by sound from the
external ear, through the middle ear, into the fluid filled cochlea. We then analyze the
mechanisms that cause the basilar membrane and the organ of Corti to vibrate which then
results in tension modulations of the hair cell stereocilia tip-links.
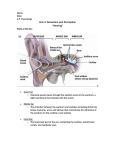
C. External ear
The external ear consists of the highly visible cartilaginous pinna flange, the cavum
concha and the ear canal buried in the skull. It is generally accepted that sound source
localization in a free field consists of two processes. The sound source azimuth is
determined using interaural time or interaural intensity, whichever is the dominant, while
sound source elevation is based on spectral cues from the pinna.
There is significant variability in both size and shape of the external ear amongst
mammals and the resulting pressure transformation from the free field to the tympanic
membrane. Examples of anatomical variations include cone shaped pinna in cats to
almost flat pinna in ferrets, numerous invaginations and protuberances of the pinna flange
and concha, and changes in ear canal cross-sectional area often accompanied by bends in
the canal. The ear canal and concha boost the sound field in the middle frequency range.
A key role of the pinna is to diffract the sound in a spatially dependent manner and thus
augment the sound field spectral cues. The torso also adds to elevation cues particularly
at low elevations and low frequencies in the form of a shadowing effect (Algazi et al.
2002).
A common measure of the effect of external ear function is the free field to tympanic
membrane pressure ratio Ptm/Pff. When measured as a function of spatial angle, the
magnitude of the ratio is often called the head related transfer function (HRTF). Not
surprisingly, the effect of the anatomical structures on the HRTF is likely unique to each
animal and varies significantly in individuals for a given species.
The transformation of the free field sound pressure to that measured at the tympanic
membrane is determined by diffraction, scattering, and resonances due to the asymmetric
structures along the way. The frequency region where different structures become
important occurs when the wavelength of sound becomes smaller than the physical
dimensions of a feature of the external ear.
1. Concha and ear-canal resonance
Dimensionally, the largest feature of the human ear with some acoustic consequence is
the ear canal, which is approximately 25 mm in length, and 7 mm in diameter with a
8
corresponding quarter-wavelength resonance near 2.5 kHz with an approximate pressure
gain of about 10 dB (Békésy 1960; Shaw and Teranishi 1968; Shaw 1974). Significant
developmental changes in the ear canal dimensions and wall properties take place even
up to the age of 24 months (Keefe et al. 1993).
The next larger feature is the concha with a height of 19 mm, a width of 16 mm and a
depth of about 10 mm. There is significant individual variation in these dimensions with
very little correlation between them or with other pinna dimensions (Algazi et al. 2001).
The depth mode resonance in the 4-5 kHz range, results in a pressure gain of about 10
dB. Both the canal and concha-depth resonances are complementary effects and are
approximately independent of angle of the free-field sound and produce a pressure gain
that starts at about 1.5 kHz reaching a maximum gain of up to 20 dB near 3-4 kHz and
then decreasing again. At frequencies above 5 kHz, the width and depth modes of the
concha becomes important and excitation of these modes is dependent on the angle of
incident sound (Shaw and Teranishi 1968; Teranishi and Shaw 1968).
2. Spatial diffraction by the Pinna
To a first order approximation, the pinna flange and the surface of the head
mechanically behave as rigid bodies to acoustic waves. In humans and in some animals
like ferrets the pinna is immobile while in other animals like mice and cats the pinna are
mobile and able to move due to muscular control independent of the skull. Many of the
mobile pinnae have a horn like structure, which improves their sound collecting ability.
The larger cone may allow an effective interaural time delay that is greater than is
possible for the head alone while the mobility allows for the possibility to modulate the
interaural time difference (Shaw and Teranishi 1968).
In humans the pinna is relatively large (64 mm x 29 mm) but it does not seem to be
strongly correlated with a resonant mode (Algazi et al. 2001). One role for the larger
pinna is to increase directivity and thus reduce background noise. There are several
unique geometric features of the pinna that contribute to resonance modes at frequencies
above 6-7 kHz. These modes are dependent on the angle of the incident sound and are
clearly important for determining the HRTFs measured in individual subjects.
The brain continually calibrates and interprets the HRTFs to infer the location of sound
indicating that there is plasticity in the perception of the spectral cues (Hofman et al.
1998). This was demonstrated by modifying the pinna of adult human subjects with a
prosthesis so as to disrupt the spectral cues resulting in poor spatial localization in the
vertical plane. However, after a relearning period of about 30-45 days the subjects were
able to localize accurately again. Furthermore, the subjects did just as well after removal
of the prosthesis suggesting that the new cues did not interfere with the perception of
previous cues.
3. Tympanic-membrane and ear-canal interface
The delicate tympanic membrane is located at the end of the long ear canal deep inside
the skull likely for protection from mechanical damage. At frequencies above
approximately 1 kHz the membrane response is very complex, while the cochlea provides
a mainly resistive load (Onchi 1961; Møller 1963; Zwislocki 1963; Khanna and Tonndorf
1969; Lynch et al. 1994; Puria and Allen 1998). This resistive load is the primary
9
damping factor of the external ear resonances.
D. Middle ear
The ear canal is filled with air that is continuous with the free field. On the other hand
the cochlea is filled with cerebro-spinal and other salty fluids. The mechanical properties
of these media are shown in Table 1. What matters for effective wave propagation is the
specific impedance, which is the product of density and wave-speed of the medium. Even
though the fluid of the cochlea has mechanical properties close to saline, the flexibility of
the cochlear partition greatly slows the wave speed, which causes a lower specific
impedancev and an air-to-cochlea impedance ratio of about 1/200. Such a large
impedance mismatch would cause most of the sound energy entering the ear canal to
reflect and not enter the cochlea.
Table 1 – Acoustical and mechanical properties of air, saline and the input widow to the
cochlea.
medium
density
ρ (kg/m3)
speed of sound
c (m/s)
Air
1.29
350
specific
impedance
z = ρc (Pa-s/m)
448
Saline
Cochlear input
1000
1000
1500
95 (approx)
1.5x106
9.5x104
impedance
ratio
β =z/zcochlea
1/212=
0.0047
15.7
1
The above shows that the slower speed of sound in the cochlea fluid reduces the air to
fluid impedance mismatch by a factor of 15.7 (24 dB). A simple model in Figure 1
illustrates this concept. The model consists of two semi-infinite tubes of cross-sectional
areas A1 and A2, with the ratio α = A1/A2, filled with fluids with the densities ρ1 and ρ2
and speeds of sound c1 and c2. The acoustic impedances are z1 = !1c1 and z2 = !2 c2 , with
the ratio β = z1/z2. The piston has one face in tube 1, and the other face in tube 2.
Figure 1: Greatly simplified
model for the middle ear
consisting of a piston
connecting two acoustic tubes.
Tube 1 represents the ear
canal, with an incident wave
and a wave reflected from the
piston. Tube 2 represents the
fluid filled inner ear with a
transmitted wave.
The hypothetical piston is free from constraint and is massless, so the force on the two
sides of the piston must be equal. An incoming acoustic wave in tube 1 (the ear canal)
10
impinges upon the piston, causing the generation of a transmitted wave in tube 2 (the
cochlea), as well as a reverse reflected wave in tube 1. The standard 1-D transmission
line analysis for acoustic waves yields the ratios of the amplitudes of transmitted and
incident pressure and energy:
E2
4!"
=
E1in
1 + !"
p2
2!
=
p1in 1 + !"
(
)
2
(Eq. 5)
The ratios for the areas of the tympanic membrane and the stapes footplate typical for
human and cat give the results in Table 2. For conduction in air, the large ratio greatly
improves the energy flowing into the cochlea. Since this is far from 100%, it is not
impedance “matching”, but rather impedance mismatch alleviation. Perfect impedance
matching αβ = 1 would provide for humans only a 15 dB improvement in the transmitted
pressure at the considerable cost of a 10 times larger tympanic membrane. It must be
noted that larger areas enhance the signal-to-noise ratio at the hair cell level (Nummela
1995).
So the large tympanic membrane is advantageous to human and cat for hearing in air. It
is interesting to consider a change to hearing under water. For this, the air in tube 1 is
replaced by water, which yields the results in the bottom section of Table 2. The acoustic
pressure transmitted to the cochlea is greatly reduced to a value insensitive to the area
ratio. The difference in pressure in air and water of 49 dB is close to the behavioral
threshold difference measured in divers (Brandt and Hollien 1967; DPA 2005). This
supports the simple relation in Eq. 5 as a fundamental consideration for the design of the
middle ear.
Table 2 – Effect of middle ear area ratio α and specific impedance ratio β in transmitting
sound pressure and energy into the cochlea, according to the basic model in Figure 1.
Replacing the air in the ear canal (tube 1) with saline simulates underwater hearing, which
has a great reduction in the transmitted pressure.
Tube 1 (EC)
β = z1/z2
Air
0.0047
Water
15.7
α = A 1/A 2
1
20 (human)
40 (cat)
212
1
20 (human)
40 (cat)
p2/p1 (lin)
p2/p1 (dB)
2
36
67
212
0.12
0.13
0.13
6
31
36
46
-18
-18
-18
E2/E1 (lin)
1.8%
25
53
100
22
1.7
0.6
In Table 3 the amplitude of the incident sound wave at threshold is given for hearing in
air and water (Fay 1988). The pinnipeds (marine mammals including sea lions, walruses,
and true seals) spend time in both air and water and have hearing sensitivity worse than
humans by a factor 10 (20 dB) in air and better by a factor of 5 (14 dB) in water.
However, the cetaceans (whales and dolphins) have better hearing sensitivity in water
than humans by factor of 54 (36 dB). It is interesting that the intensity of the sound at
threshold is about the same for human in air and pinniped in water, and for human in
water and pinniped in air. Obviously, the middle ear of the pinniped is designed for the
11
water environment. Quite a different middle ear design provides the extraordinary
sensitivity under water of cetaceans (Hemila et al. 1999).
Table 3 – Some approximate thresholds of hearing in air and water.
Human
Pinnipeds
Cetaceans
Pressure
(µPa)
20
200
-
Air
Intensity
(Watts/m2)
8.9 x10–13
8.9 x 10–11
-
Pressure
(µPa)
5400
1000
100
Water
Intensity
(Watts/m2)
2 x 10–11
6.7 x 10–13
6.7 x 10–15
As the simple estimate indicates, without an effective middle ear, the sensitivity of the
cochlea would be compromised and so would the overall bandwidth as is evident by
pathological conditions of the ear repaired by otologists. As discussed in a subsequent
section, another important role of the middle ear is in exerting some degree of dynamic
range control at high input levels via the three sets of muscles.
The simple model of Figure 1 is useful to certain degree but has significant limitations.
In order to build an acoustic lever with an area change from the ear canal to the cochlea
requires using biological materials consisting of bone and soft tissues. A rigid piston with
a large area requires a large mass, which limits its ability to transduce sound particularly
at the higher frequencies. A membrane is lighter but has a significant number of resonant
modes particularly at frequencies above 2-3 kHz. In a very thorough study, Nummela
(1995) show that malleus and incus masses scale with eardrum area, which further limits
high frequency hearing. These factors must be considered when formulating
mathematical models of the middle ear.
More sophisticated models describing sound transmission in the middle ear have been
around for some time. Early studies allocated various acoustic influences to the different
middle ear structures interconnected in 5-6 functional blocks. The blocks were then
assigned more detailed elements, which consist of masses, springs, and dashpots. Some
of the earliest models by Onchi (1949; 1961), Zwislocki (1961), and Møller (1961) use
dynamic analogies and represent the middle ear in the form of electrical circuit models.
These phenomenological models have evolved and continue to be useful for
understanding surgical interventions of the middle ear (Rosowski and Merchant 1995;
Merchant et al. 1997; Rosowski et al. 2004). Nevertheless, they have limitations in that
there is not a tight relationship between the underlying anatomical structure and function.
To overcome these limitations requires models that explicitly incorporate morphometry
of the middle ear into the formulation.
1. Tympanic membrane shape and internal structure
There remain many unanswered questions regarding the biomechanics of the tympanic
membrane. For example, why does the tympanic membrane have a conical shape? Why
do the tympanic membrane sublayers have a highly organized collagen fiber structure?
What is the advantage of its angular placement in the ear canal? Why is there
symmetrical malleus attachment to the eardrum in some animals while in others there is
asymmetry? The functional significance of many of these gross anatomical features of the
12
tympanic membrane is just beginning to be understood and current status is discussed
below.
Helmholtz (1868) discussed the need for impedance matching of the air in the
environment and the fluid of the inner ear and suggested that the tympanic membrane
behaved as a piston. This assumption is widely used in lumped parameter (circuit) models
of the middle ear, which build upon the free piston model (Eq. 5) by adding springs and
the resonances of the malleus-incus complex and of the middle ear cavity. However,
instead of piston behavior, surface displacement measurements revealed multiple modes
of vibration for frequencies above a few kHz (Tonndorf and Khanna 1972). Since the toand-fro motion of a resonance mode would reduce the effective area for the sound
pressure, the presence of these modes has been difficult to explain. Pioneering work by
Rabbitt and Holmes (1986) formulated a continuum analytic model with asymptotic
approximations for the cat tympanic membrane. They included the membrane geometry
and anisotropic ultrastructure in combination with curvilinear membrane equations, but
did not analyze the effects of the eardrum angle and the conical shape of the eardrum, nor
have Eiber and Freitag (2002). Current finite-element models represent the eardrum as an
isotropic membrane (Wada et al. 1992; Koike et al. 2002; Gan et al. 2004) and thus do
not explain the need for the detailed fiber structure (Lim 1995).
Two breakthroughs have increased our understanding of tympanic membrane
mechanics. First, was the observation that there is significant acoustic delay in eardrum
transduction (Olson 1998; Puria and Allen 1998). Second, the multiple modes of
vibration seen on the surface of the eardrum are not transmitted to the cochlea. Rather,
the pressure inside the cochlea as a function of frequency remains relatively smooth, even
when measured at a high frequency resolution (Magnan et al. 1997; Puria et al. 1997;
Olson 1998; Aibara et al. 2001; Puria 2003). Clearly these observations are tied to the
complicated motions of the eardrum observed by Khanna and Tonndorf (1972) but need
explanation.
2. Tympanic Membrane Biomechanics
To understand the functional consequences of the tympanic membrane structure on its
sound transducing capabilities, a biocomputation model has been formulated which leads
to some insights on the posed questions (Fay 2001; Fay et al. 2006). The model
incorporates measurements of the geometry of the ear canal (Stinson and Khanna 1994),
the 3-D cone shape of the eardrum (Decraemer et al. 1991), and details of the eardrum
fiber structure (Lim 1995).
13
Figure 2: Human eardrum photograph with its biomechanical model representation composed of
adjacent wedges. The zoomed box shows the four layer composite of each wedge. The inner radial and
circumferential collagen fiber layers, unique to mammals, provide the scaffolding for the tympanic
membrane. Dimension and material property differences of the wedges lead to mistuned resonances at
high frequencies. The thickness of the eardrum layers increases from the umbo to the tympanic annulus.
The discrete model for the human eardrum is shown in Figure 2, in which a series of
adjacent wedges approximate the eardrum. Near the center, the eardrum is attached to the
malleus, while the outer edge is attached to the bony annulus (not shown). The 1-D
acoustic horn equation is used for a small cross-section of the ear canal. The change in
area from the adjacent section, the curvature of the centerline, and the flexibility of the
portion of the eardrum that intersects with that section of the ear canal are taken into
account. Each strip of the eardrum has a curvature near the outer edge (locally a toroidal
surface) and is straight in the central portion (locally conical). Because the main conical
portion has few circumferential fibers, the approximation is that the radial strips are
weakly coupled in the circumferential direction.
The tympanic membrane is represented as a four-layer composite (Figure 2). The input
14
parameters for the formulation are the thickness of each layer as a function of position
and the Young’s modulus of elasticity (a measure of resistance to deformation) for each
layer. The outer most epithelial layer and the inner most submucosal layers are relatively
flexible. Because the sub-epidermal layer and the sub-mucosal layers consist of
connective tissue and are also relatively flexible, they are part of the epidermal and
mucosal layers respectively (Figure 2). The inner two layers have collagen fibers that are
radially oriented in one layer and circumferentially oriented in the layer directly below.
These two layers, unique to mammals, provide the majority of the scaffolding for the
eardrum and thus those layers mostly determine the compliance of the membrane. The
mass on the other hand comes from overall thickness of the membrane. Quantitative
measurements for cat were used for the overall thickness (Kuypers et al. 2005). From
these measurements and from sparse measurements of collagen sublayers, the thickness
of each sub layer was estimated for human (Figure 2) and cat (Fay et al. 2006; Fay et al.
2005).
Direct measurements of the static elasticity of portions of the eardrum (Békésy 1960;
Decraemer et al. 1980) indicate an effective modulus of elasticity of around 0.03 GPa.
This was re-examined using three very different methods to determine the eardrum
modulus of elasticity (Fay et al. 2005). First, constitutive modeling incorporating the
Young’s modulus of collagen and experimentally observed fiber densities in cat and
human were used. Second, the experimental tension and bending measurements (Békésy
1960; Decraemer et al. 1980) were reinterpreted using composite laminate theory. And
third, dynamic measurements of the cat surface displacement patterns were combined
with a composite shell model. All three methods lead to similar modulus of elasticity
value of 0.1-0.4 GPa for near the center of the eardrum. The corresponding values near
the outer edge are approximately ½ these values due to the liner taper in the elastic
modulus. In previous models the eardrum is treated as a single layer having a uniform
elastic modulus resulting in a low value of elastic modulus (Funnell et al. 1987;
Prendergast et al. 1999; Koike et al. 2002; Gan et al. 2004). In the four-layer model, the
collagen fiber sub layer is much thinner than the overall thickness and hence the
estimated elastic modulus is higher.
The modulus of elasticity was combined with the sub layer thickness to formulate a
complete model of the cat tympanic membrane. The calculation for the dynamic response
of each strip was performed with an algorithm for elastic shells (Steele and Shad 1995),
which has no restriction on wavelength along the strip.
15
Figure 3: Effect of modification of the eardrum depth. (a) In the center is the anatomically normal eardrum. The zcoordinate of all the points is divided by a factor of 10 to obtain the shallow eardrum on the left, and multiplied by a
factor of 2 to obtain the steep eardrum on the right. (b) Effect of eardrum depth on the middle ear pressure transfer
function, which is the ratio in dB of the pressure delivered to the vestibule inside the cochlea (pv) divided by the input
pressure in the ear canal (pec). The deep eardrum calculation is nearly the same as the normal, but the shallow
eardrum has more than a 20 dB loss at higher frequencies. For the normal and deep eardrums, the phase delay is
steeper than it is for the shallow drum, indicating more acoustic delay. (Reproduced from Fay et al., 2006 with
permission).
The full 1-D interaction of the air in the ear canal and the eardrum is included. Behind
the eardrum are the middle ear cavities and the middle-ear bones connected to the
cochlea, for which lumped-element approximations were used. Verification involved
mesh refinement studies, comparison with exact solutions for limiting cases, anatomical
values of geometry, best estimate for elasticity, and comparison with physiological
measurements to 20 kHz, all for the cat middle ear.
Different depths of the eardrum play an important role as shown in Figure 3. With a
shallow eardrum (no cone shape) there is a loss of more than 25 dB for frequencies above
about 4 kHz (Figure 3b, top panel). A deep eardrum shows a response similar to that seen
in anatomic specimens, with little loss for low frequencies. Above 4 kHz, the phase for
the normal and deep eardrum continues to decrease while for the shallow drum the phase
tends to go in the opposite direction and increases. This suggests that there is more phase
delay for the deep and normal shape than for shallow eardrums. In comparison to the
16
normal eardrum the deep drum requires more real estate in the skull, which competes for
space with other organs.
The effect of the two collagen-fiber sub-layers was also analyzed. This was done by
examining the effects of isotropic eardrums that had the same stiffness in the radial and
circumferential directions and orthotropic eardrums where there were radial fibers but no
circumferential fibers (Fay 2001; Fay et al. 2006). Results indicate that there is an
advantage of the orthotropic microstructure with a dominance of radial fibers in the
central region. In the normal drum when both are present, the radial fibers on the inner
portion of the tympanic membrane result in an effectively orthotropic membrane while
the outer circumferential fibers provide a low-impedance beam-like support. The
orthotropic central portion allows maximal sound transmission at both low and high
frequencies.
The model calculations indicate that sound transmission from the ear canal to the
cochlea varies smoothly despite the fact that there are a significant number of resonances
at different points on the eardrum. This suggests a design where drum sections are
deliberately mistuned. Because these resonant points are added together at the malleus,
no single mode ever dominates. Thus the ensemble of eardrum modes produces a
relatively large and yet fairly smooth response at the malleus at the higher frequencies.
Understanding of eardrum biomechanics is of critical importance to the development
and improvement of “myringoplasty” which is a surgical procedure for repairing
damaged eardrums. The underlying disease process is often chronic inflammatory disease
of the middle ear and mastoid, referred to as chronic otitis media (COM), which leads to
a partial or total loss of the tympanic membrane or ossicles. Clinically, isotropic materials
like temporalis fascia are used for myringoplasties. To improve hearing results at the
higher frequencies, orthotropic material with collagen scaffolding preferentially oriented
in the radial direction would be a better choice for improved high frequency hearing
outcomes. Improving post-operative high frequency results may be important for the
perception of sound localization cues present at high frequencies. Currently the standard
practice is to measure clinically to 6 kHz. The above results suggest that clinical
measurements at frequencies above 6 kHz might better show the effects of different
materials.
Since the modulus of elasticity and the biocomputation approach using asymptotic
methods is already developed for the cat, the challenge will be to estimate eardrum
morphometry for other species such as human (Figure 2 shows an approximate guess). Of
particular interest is determining how the shape and thickness of the tympanic membrane
varies from subject to subject. Such quantification will allow for the possibility of using
the eardrum biocomputation on individual subjects. Non-destructive high-resolution
imaging methods are needed to obtain morphometry on individual subjects. A promising
new imaging technology is described in the next section.
3. Middle ear imaging
To obtain morphometry of the ear, histological methods have been the primary
technique. However, this age old technique is destructive and certainly not appropriate
for in-vivo imaging of individual subjects. One of the most recent advances for obtaining
anatomical information is micro computed tomography (microCT). This has been used to
17
obtain volume reconstructions of the temporal bone of living subjects at a resolution of
less than 125 µm (Dalchow et al. 2006). In-vitro resolution can be increased by an order
of magnitude (Decraemer et al. 2003).
Figure 4: MicroCT image of an
intact cadaver temporal bone. This
is image #769, of 1897 images
spanning a length of 28.455 mm.
The image illustrates that most of
the middle ear structures can be
visualized from an intact temporal
bone ear scan. The resolution for
both in-plane and out-of-plane
(slice thickness) is 15 µm. The
tympanic
membrane
although
visible is faint, suggesting that
the basic geometry and an
approximate thickness can be
obtained. The 30.72 mm scan
diameter outline is clearly seen.
Figure 4 shows an image slice from an intact human cadaver temporal bone ear. The
image resolution in the x, y, and z planes is 15 µm (iso-volume). Most of the middle ear
structures, including the tympanic membrane cone shape and thickness, ossicles, and
suspensory soft tissue, can be visualized because there is good density contrast between
these structures and air in the ear canal and middle ear cavity. Because they provide the
best resolution, histological methods remain the standard. However, µCT imaging offers
some distinct advantages (Decraemer et al. 2003). These include: (1) elimination of
stretching distortions commonly found in histological preparations, (2) use of a nondestructive method, (3) shorter preparation time (hours rather than 12-16 months), and (4)
results already in digital format. This imaging technology is rapidly evolving and it is
likely that similar resolutions will be possible for in-vivo imaging in the near future.
4. Malleus-incus complex
The middle ear of most non-mammalian terrestrial animals consists of the tympanic
membrane and a columella, while mammals have a tympanic membrane and a malleusincus complex. Amongst vertebrates a great majority of mammals are sensitive to
ultrasonic sounds (above 20 kHz), while non-mammals are notvi. This suggests that the
mammalian hearing organ evolved to be a superior organ for high-frequency response
compared to that of non-mammals and that the incorporation of the malleus-incus
complex may have something to do with this capability (Fleischer 1978; 1982). However,
the biomechanics of this sub system of the middle ear are not well understood.
Since the time of Helmholtz (1868) the handle of the malleus and the long process of
the incus were described as the two arms of a lever with a fixed axis. Ossicle suspension
also further supported the notion that the malleus and the incus rotate about a fixed axis
18
while driving the stapes in a piston like manner. However, detailed measurements of the
ossicles have changed this view (Decraemer et al. 1991; Decraemer and Khanna 1995).
The malleus motion changes with frequency and all 3-D components of translation and
rotation are present at biologically relevant stimulation levels. These measurements
suggest that a full 3-D model of ossicle motion is required.
Between the malleus and incus is a saddle-shaped joint formed from an indentation in
the head of the malleus into which the surface of the body of the incus fits (Figure 5). The
incus also has a depression into which a part of the malleus head fits, forming a cog-like
mechanism as described by Helmholtz (1868). The significance of such a mechanism is
thought to be a locking of the joint causing one part to move with the other during
rotation in one direction but leaving the parts free to rotate in the orthogonal direction
(Wever and Lawrence 1954). However, measurements (e.g., Helmholtz 1868; Békésy
1960) suggested that the incus and malleus are fused together indicating that there is no
slippage at the incudo-malleolar joint (IMJ). Making measurements in the cat ear, Guinan
and Peake (1967) showed clear evidence of slippage at the IMJ above about 8 kHz. Using
time-averaged holography measurements Gundersen and Høgmoen (1976) concluded that
the “malleus and incus rotate like one stiff body” for frequencies below about 2 kHz. Due
to these measurements, mathematical models of the human middle ear generally treat the
two ossicles as fused and do not include slippage (Goode et al. 1994; Koike et al. 2002).
More recent measurements suggest slippage between the incudo-malleolar joint and lack
of slippage in previous measurements was possibly due to methodological reasons
including a possible lack of a cochlear load and insensitive measurement techniques
(Willi et al. 2002). In some animals, like guinea pig and chinchilla, the IMJ is fused and
thus there is no slippage (Puria et al. 2006). On the other hand, there is no controversy
regarding slippage at the joint between the incus and the stapes, and most mathematical
models currently include it (e.g., Goode et al. 1994).
Natural mode shape calculations indicate that the ossicles can be treated as rigid bodies
only for frequencies below about 3.5 kHz (e.g., Beer et al. 1999). Consequently, the
ossicles have been modeled as finite elements, which require much more computation
time. An alternative approach is to model the ossicles as elastic bodies incorporating just
the first two or three modes in each body (Sim et al. 2003).
Not unlike the biological ligaments found in other parts of the body, the suspensory
ligaments and tendons of the middle ear are a composite, consisting of collagen and
elastin embedded in an amorphous intercellular material often called ground substance or
matrix which is composed of proteoglycans, plasma constituents, metabolites, water and
ions. Almost two-thirds of the weight of ligaments is water, while about three-quarter of
the remaining weight can be attributed to the fibrillar protein collagen (reviewed by
Weiss and Gardiner 2001). Like the eardrum, the primary component resisting tensile
stress in ligaments and tendon is collagen. The primary role of the ground substance is in
maintenance of the collagen scaffolding. As such, the biomechanical behavior of a
ligament is determined by its geometry, shape of the articulating joint surfaces,
orientation and type of insertions to bone, in-situ pretension, and material properties.
What role do the suspensory ligaments play in the complicated 3-D vibrations of the
middle ear bones? This question has yet to addressed with any degree of satisfaction.
In the cat study discussed above, a simple ball and stick model for the malleus-incus
complex was used (Fay et al. 2006). This was a gross simplification but allowed
19
concentration on the tympanic membrane biomechanics. A goal of several laboratories is
to combine anatomical data with human cadaver temporal bone malleus-incus complex 3D motions into a computational model for individual ears, which should increase
understanding of the functional consequences of the anatomy of the ossicles and
suspensory ligaments and tendons.
a)
b)
Figure 5 : Volume reconstruction of the malleus and incus from uCT slices. (a) The incus is made transparent to allow
better visualization of the incudo-malleolar joint. (b) The incudo-malleolar joint saddle shape and thickness map (0 is
dark green while about 300 µm is red).
The biomechanical characterization of the malleus-incus complex requires
morphological and dynamical measurements from individual ears. The center of mass,
moments of inertia, anatomical location and orientation of the ligaments and tensortympani tendon, are obtained from 3-D volume reconstructions (Figure 6) based on µCT
images of the isolated preparation.
Figure 6: Three-dimensional
volume reconstruction of the
malleus,
incus,
suspensory
ligaments and the tensor tympani
tendon. The soft tissue is
represented as tapered cylinders
or as a polyhedron. The origin is
at the umbo. All dimensions are
in mm.
The morphometry is used to construct a computational biomechanical model for the
malleus-incus complex that includes ligament and tendon attachments to the bony walls
and muscle, and slippage at the incudo-malleolar joint. Bending of the malleus and incus
20
handles is also allowed. The viscoelastic parameters of each ligament, tensor tympani
tendon, and the incudo-malleolar joint cannot be determined from the morphometry and
thus 3-D motion measurements are required.
As discussed in previous sections, the biomechanics of the tympanic membrane can be
fairly complicated. This implies that the input to the malleus-incus complex is also
relatively complicated and thus it is difficult to deduce the dynamics of ossicles and soft
tissue attachments with the sound driven eardrum. To better understand ossicle dynamics
an isolated malleus-incus complex preparation was developed where the tympanic
membrane and the stapes were dissected. Without an eardrum or a cochlea, the middle
ear bones have to be directly driven. A tiny magnet and a coil around the tympanic
annulus were used to drive the malleus-incus complex (Sim et al. 2003). The magnet on
the tip of the malleus is oriented to drive it in the forward direction. The preparation is
placed on a set of goniometers and malleus-incus motion measurements made at several
points at several different angles. The resulting three-dimensional x, y and z vector
components of velocity at each point is used within the biomechanical model to obtain
the soft tissue viscoelastic parameters. The 3D volume reconstruction of the magnet and
coil combined with electro-magnetic theory allows accurate calculation of the 3D forces
and moments exerted by the magnet to the malleus. The combined, imaging, physiology
and biomechanics approach should help us better understand the structure and functional
relationships at audio frequencies in normal and pathological ears.
The above discussion concerns the dynamics of the malleus-incus complex. At high
positive and negative static pressures such as during sneezing and coughing the
suspensory ligaments may also play a critical role (Huttenbrink 1989). Incorporation of
this mode of operation requires extension of the linear models to non-linear models.
5. Lenticular process
The inferior end of the long process of the incus terminates in a short perpendicular
bend called the lenticular process consisting of the pedicle and the lenticular plate
surrounded by soft tissue. Between the lenticular plate and the stapes head is the incudostapedial joint. Motion from the incus is transmitted to the stapes via this process and thus
its mechanical description is of significance.
Most previous modeling work has treated the lenticular process to be a rigid bone that
transmits the incus motion directly to the stapes head or with a slippage representing the
incudo-stapedial joint (Beer et al. 1999; Koike et al. 2002). Recent anatomical
measurements suggest that the plate-like bony pedicle is perpendicular to the lenticular
plate and is extremely thin and fragile. In cat the dimensions of the pedicle are 240 µm x
160 µm x 55 µm (Funnell et al. 2005). Model calculations of static displacements suggest
that there is significant relative motion between the incus long process and stapes head
(Funnell et al. 2005). Funnell and colleagues have hypothesized that one role for the thin
pedicle and lenticular plate arrangement may be to convert the rotational modes of
vibration of the incus into translational motion of the stapes. More work is needed to
further test this hypothesis.
It has been observed that at high static pressures, there is a large lateral displacement of
the lenticular process and this serves to protect the cochlea from large motions
(Huttenbrink 1988). Clearly, bending of the pedicle may be involved.
21
6. Stapes
The interface between the malleus-incus complex and the vestibule of the fluid filled
cochlea is the stapes, which is held in place in the oval window (Fenestra vestibule) by
the annular ligament. The mechanics of the stapes is quite independent of the malleusincus complex and of the cochlear fluid load. For this reason the stapes can be considered
a semi-independent sub system of the mammalian ear (Fleischer 1978). This treatment of
the stapes is widely accepted (Wada and Kobayashi 1990; Wada et al. 1992; Goode et al.
1994; Puria and Allen 1998; Beer et al. 1999; Koike et al. 2002).
7. Ossicular reconstruction
While we are discussing the ossicles this is good place to discuss ossiculoplasty, which
is the reconstruction of the middle ear bones to improve hearing sensitivity. Two of the
most common pathologies are missing (or eroded) incus and ossified stapes. Both result
in significant conductive hearing loss. Since the introduction of these surgical procedures
more than fifty years ago, ossiculoplasty continues to pose significant challenges to
otologists.
The interposition of passive prostheses between the malleus or tympanic membrane
and the stapes head or footplate is used to reconstruct the transfer function of the middle
ear in the missing or eroded incus condition. These are the incus replacement prostheses.
Two types, depending on the circumstance, are the partial ossicular reconstruction
prosthesis (PORP) to the stapes head while another is the total ossicular reconstruction
prosthesis (TORP) to the stapes footplate. The PORP is typically used if there is an intact
stapes superstructure. However, ear canal pressure to cochlear pressure transfer function
and clinical measurements suggest that even if the stapes superstructure is present there
are acoustico-mechanical advantages to placing the foot of the prostheses on the footplate
(Murugasu et al. 2005; Puria et al. 2005).
In a very different disease process called otosclerosis, the stapes becomes fixed to the
surrounding oval window through ossification. The immobile stapes prevents sounds
from entering the cochlea and results in significant hearing loss. The precise cause of
otosclerosis is not well understood. However, it is becoming well established that
otosclerosis is hereditary. Otolaryngologists repair the condition by a procedure called
stapedotomy. A hole is made in the footplate often with a surgical laser (Perkins 1980)
and then covered with soft tissue to prevent the inner ear fluid perilymph from leaking
out. Sound transmission is restored with a piston like prosthesis. One end of the
prosthesis is crimped to the long process of the mobile incus while the other end is
inserted in the covered artificial hole in the footplate.
8. Middle-ear muscles
The malleus and stapes each have a tendon attached to a tiny muscle, the tensor
tympani muscle and the stapedius muscle respectively. The muscles contract when
exposed to high level sounds and are part of the middle ear reflex arc involving the spiral
ganglion neurons, the auditory nerve, cochlear nucleus, the superior olive, the facial
nerve nucleus, the facial nerve and the two middle ear muscles (Margolis 1993). This
reflex arc can reduce sound transmission through the middle ear at high levels and may
serve to control the dynamic range of the auditory system and to protect the cochlea at
22
high sound levels. The reflex is slow and thus does not provide protection to the cochlea
against sudden impulsive sounds. The time for the stapedius reflex may be on order of
about 20 ms while the tensor tympani arc is more than ten times slower.
Two additional functions are attributed to the middle ear muscle reflex. Low frequency
sounds, particularly when they are high in level, normally tend to mask mid and high
frequency sounds due to their upward excitation patterns on the basilar membrane. One
role of the middle ear muscles is to reduce the level of low frequency inputs so they do
not mask the higher frequency sounds on the basilar membrane (Pang and Guinan 1997).
A second role of the middle ear reflex is in the reduction of the audibility of generated
sounds during speech, mastication, yawning and sneezing (Simmons and Beatty 1962;
Margolis and Popelka 1975). Because the reflex arc involves so many mechanisms, its
measurement is clinically used to diagnose central and peripheral pathologies.
Recently it has been discovered that there are smooth muscle arrays on the peripheral
edge, annulus fibrous, of the tympanic membrane in all four (bats, rodents, insectivores,
and humans) of mammalian species studied (Henson and Henson 2000; Henson et al.
2005). The role of this rim of contractile muscle cells in the par tensa region is not clear,
but two suggested possibilities are to maintain tension of the tympanic membrane and to
control blood flow to the membrane (Henson et al. 2005). Measurements indicate that
these smooth muscles can exert control over the input to the cochlea as measured by
cochlear microphonics (Yang and Henson 2002).
9. Middle-ear cavity
One role of the middle-ear cavity is to act as a baffle for the tympanic membrane so
that sound does not impinge on both sides of the eardrum. Without this, the sensitivity of
the membrane, and thus hearing sensitivity, would be significantly reducedvii. However,
the presence of the cavity results in an increase in overall impedance, due to volume
compliance, at low frequencies and resonant modes at high frequencies. An increase in
middle ear impedance results in a decrease in hearing sensitivity (Wiener et al. 1966).
In humans the middle ear cavity is relatively large but is irregular in shape. The
mastoid cavity portion has many air cells, or air pockets, that results in an increase in
surface area. Each cell is lined by a mucous membrane of thin epithelial cells. It is
thought that the irregular shape minimizes resonant modes and the air cells effectively
dampen remaining resonance (Fleisher, 1978).
10.
Middle-ear acoustic load
The primary load to the middle ear is the acoustic input impedance of the cochlea Zc.
As defined by Zwislocki (1975), Zc is the ratio of sound pressure in the scala vestibuli at
the stapes footplate to the volume velocity of the footplate. Based on simplifications to
the equations of motion at the base of the cochlea, Zwislocki (1948; 1965; 1975)
predicted that the cochlear input impedance is primarily resistive. Direct measurements in
the cat (Lynch et al. 1982), guinea pig (Dancer and Franke 1980), and human cadaver
ears (Aibara et al. 2001) suggest that the prediction by Zwislocki was essentially correct
for a broad range of frequencies.
Zwislocki’s calculation had not included effects from the apical region of the cochlea.
Calculations of the cochlear input impedance in the constant scalae area standard box
23
models of the cochlea, that include the apical region, shows that below approximately 1-2
kHz, the cochlear input impedance magnitude decreases and becomes more mass like.
This calculated result diverges from the measured data and from Zwislocki’s prediction
(Puria and Allen 1991; Shera and Zweig 1991). The decrease in the acoustic impedance
and mass like response is shown to be due to the use of constant cross sectional area for
the scala vestibule and scala tympani in all standard box models. Using a more realistic
scalae area that decreases from base to apex of the cochlea avoids the diverging
catastrophe in the model calculations of cochlear input impedance at low frequencies.
The resistive nature of the cochlear input impedance, which is the primary damping
component of sound transmission in the middle ear, has two consequences. Foremost is
that a large fraction of the acoustic energy that enters the cochlea is absorbed by it rather
than being reflected by it. Second, is that it smoothes out the peaks and valleys resulting
from any resonances in the middle ear structures.
E. Cochlear hydrodynamics
In the preceding section, methods of imaging, physiology, and computational
biomechanics were presented in the context of understanding the relationship between
acousto-mechanical transformations of sound by the middle ear. The end result is that the
proximate output variable of the middle ear, which is the vestibule pressure at the base of
cochlea, smoothly varies with frequency and typically with pressure gain for a wide
bandwidth relevant to the specific species. In the following sections we analyze how
sound energy at the base of the cochlea propagates in the cochlea. Much effort has been
devoted to this topic, on which many survey papers have been written, as represented by
Allen and Neely (1992), Nobili et al. (1998), and deBoer (1991). DeBoer (2006) provides
a summary of current thought. In addition, other articles in this Handbook address
different aspects of cochlear function. Our focus is on what appear to be key acoustomechanical mechanisms that have a basis in the physiology.
1. Vestibule pressure
A simple description of what happens to the pressure transmitted into the cochlea by
the middle ear is shown in Figure 7 for a given frequency. This represents a standard
tapered box model for the cochlea with two symmetric fluid ducts divided by a partition.
The stapes provides the input pressure. The wall of the cochlea is bone, which is
normally assumed to be rigid, so for air-conducted sound the stapes and round window
have equal and opposite volume displacement, preserving the volume of fluid in the
cochlea. However, a very compliant membrane covers the round window, so the fluid
pressure at this point is nearly zero. Therefore the total pressure is divided into an “even”
and an “odd” solution (Peterson and Bogert 1950), as indicated in Figure 7. The even
distribution must cause a compression of the fluid. This corresponds to a wave that
travels with the speed of sound in the fluid, which is relatively “fast”. The odd solution
produces net pressure acting on the partition that causes an elastic deformation of the
flexible portion of the partition, the basilar membrane (BM). This interacts with the fluid
motion, causing a wave that is relatively “slow”. This slow wave is the “traveling wave”
first observed in the guinea pig by Békésy (1952). Because the BM is narrow at the
stapes and wide at the apex, there is a gradient in stiffness of the partition, which causes
24
the traveling wave to have a long wavelength near the stapes, then build up to a
maximum as the wavelength becomes short. In the very short wavelength region, the
viscosity of the fluid causes this wave to die out exponentially. The traveling wave is so
slow, relative to the fast wave, that the fast wave can often be approximated as
instantaneous, i.e., for incompressible fluid.
For simplicity, we consider the properties of the partition to be continuous. The actual
tissue consists of discrete elements. As shown by Békésy (1960, p. 510) by models with
coupled, discrete elements, behavior similar to that of a continuous system can be
obtained. This holds, of course for wavelengths of response that are long in comparison
with the spacing between elements. Many authors use discrete systems directly for
advantage in computation and/or construction.
The description in Figure 7 for the spatial distribution for a fixed frequency also holds
for the waves seen at a fixed point as frequency varies. For frequencies less than the best
frequency (BF), the slow wave has long wavelength, and for frequencies greater than BF,
the slow wave decays to negligible magnitude, leaving only the fast wave.
Figure 7: Simple tapered box model for the pressure in the cochlea. The fluid regions scala vestibuli
(SV) and scala tympani (ST) with tapered areas are divided by the partition containing the elastic
basilar membrane (BM). At the apex the partition has an opening, the helicotrema. The input sound
pressure acts at the round window (stapes). The response for a single frequency is divided into an
even (symmetric) solution with equal pressure in SV and ST, and an odd (asymmetric) solution with
the pressures in SV and ST of opposite sign. The symmetric solution causes a compression of the
fluid, so the wave travels with the speed of sound in saline, which is the “fast wave” in the upper
drawing. In contrast, the asymmetric solution has a net pressure on the partition, which causes a
displacement of the BM that slows the wave considerably. This is the “slow wave” in the lower
drawing. Because of the taper of the BM the stiffness changes and the slow wave has a wavelength
that is long near the input but becomes short near the region of maximum amplitude. The driving
frequency is the “best frequency” (BF) for this “place”. In the region of short wavelength, the fluid
motion is 3-D, with a pressure that is maximum on the BM and decays exponentially with both the
distance from the BM and the distance toward the apex. The round window is compliant, so the total
25
fluid pressure at that location is nearly zero. Thus at the input end, the pressures from the slow and
fast wave must cancel in ST and so are equal in magnitude.
The first direct evidence for this behavior is provided by the measurement of pressure
in the gerbil (Olson 1998) at a distance 1.2 mm from the stapes. Some of the
experimental values are shown in Figure 8, along with calculated values from a 3-D
cochlear model to be discussed later. Near BF the pressure is strongly dependent on the
distance from the BM, with much larger values near the BM (Figure 8a). This shows the
3-D behavior of the fluid in the short wavelength region. For low frequencies, the
pressures at the different distances from the BM converge, showing the long wavelength
region. The phase response shows the near cancellation of the waves for low frequencies
(Figure 8b). For higher frequencies the slow wave dominates, and the rapid accumulation
in phase is characteristic of a traveling wave. For even higher frequencies, the traveling
wave disappears, so all that is left is the fast wave with constant phase, which at different
distances from the BM differ by one cycle, so these are in fact the same. The phase
measurements show that far from the BM (305 µm) the traveling wave quickly
disappears, while the points closer (3 – 228 µm) all have the same phase. In contrast, the
calculation shows differences at these points. This may be due to the large pressure probe
interfering with the fluid motion, which is only simulated in the calculation by taking the
average of the pressure at nine points in the 100 µm diameter of the probe. This is for 80
dB SPL input eardrum pressure. The measured pressure shows a constant value for high
frequency equal to 100 dB SPL. This corresponds to the 80 dB input to the eardrum, with
a 26 dB gain through the middle ear, and a 6 dB drop because the fast wave has half the
amplitude of the vestibular pressure at the stapes.
Figure 8 (a): Pressure magnitude in the
cochlea at the distance 1.2 mm from the
stapes in ST measured in the gerbil (Olson
1998) and calculated (Baker 2000). For
frequencies higher than BF (> 40 kHz), the
slow wave is negligible and only the fast
wave remains (Figure 7). For low
frequencies, the fast and slow waves
nearly cancel in ST. Near BF (25 kHz), the
fast wave dominates, with 3-D fluid
motion that has much higher pressure
near the BM. The discrete points x show
the measurements at the distances from
the BM of 3 and 305 µm, while the
calculated
values,
shown
by
the
continuous curves, include distances in
between.
Figure 8(b): Pressure phase relative to the
simultaneously measured scala vestibule
pressure at the base of the cochlea. For
frequencies above BF (> 40 kHz), only the
fast wave remains. The plateaus differ by
one cycle, which shows that the fast wave
is uniform with distance from the BM and
exactly in phase with the eardrum
pressure. For low frequency, the phases at
the different distances from the BM are
26
also the same, corresponding to the fast
wave and the long wavelength region of
the slow wave. For frequency approaching
BF (25 kHz), the slow wave dominates and
shows the rapid decrease in phase
signifying the traveling wave.
2. Partition resonance
At one time or another almost every component of the cochlea has been suggested as a
key tuned resonator that will cause a significant local response for a given frequency (the
BF in Figure 7). The basilar membrane (BM) is the thin compliant portion of the partition
that divides the two fluid ducts in Figure 7. The component for which the tuning can be
best related to the physical dimensions is the pectinate zone of the BM. Mathematical
treatments of the BM include both bending stiffness and tension in addition to their
interaction with the surrounding fluid. From the mathematical formulation, the frequency
range and the place to frequency map of the cochlea given the anatomical dimensions
with material properties can be predicted.
a) Plate
A cross section of the basilar membrane is sketched in Figure 9. For many mammals,
the BM pectinate zone consists of a sandwich of collagen fibers in the radial (y) direction
embedded in amorphous ground substance. For the same amount of material thickness,
the sandwich provides increased bending stiffness. For simplicity, the details of the
sandwich are omitted, and only the motion in the cross section (y–z plane) is considered.
For such a plate, the equation of motion in response to an applied pressure is:
D
!4 w
!2 w
!2 w
"
T
+
#
t
= "2 pF
P P
!y 4
!y 2
!t 2
(Eq. 6)
in which w is the displacement of the plate, T is the tension, ρP is the plate density, tP is
the plate thickness, pF is the pressure in the fluid above the plate, which is doubled in Eq.
6 for fluid above and below the plate, and the bending stiffness is D = f Et P3 12 , where E
is the Young’s modulus of the fibers and f is the volume fraction of the fibers. For hinged
edges at y = 0 and b, the solution is:
w = We j! t sin ny
n =! /b
(Eq. 7)
in which W is the amplitude and ω the frequency. For static loading and for zero tension,
the results for the volume stiffness and point load stiffness are:
27
K Vol =
2 pF !
= Dn5
bw 8
kPtL =
P 48Dd
=
W
b3
(Eq. 8)
where w is the average displacement, and P is the magnitude of a load on a probe at the
center with diameter d. With all terms retained, Eq. 6 gives the impedance, the relation
between the pressure and velocity v = w! :
(
Dn4 + Tn2 ! tP "P# 2
2 pF
=!
v
j#
)
(Eq. 9)
Figure 9: Cross section consisting of an
elastic plate in vacuum with tension T. The
plate thickness is t and the width between
the support points is b. The resonant
1/ 2
frequency is proportional to T / tb 2
.
The dashed line shows
position of the plate.
( ( ))
the
deformed
Figure 10: Cross section consisting of an
elastic plate in infinite fluid. When the
density of plate and fluid are the same, the
plate density is negligible, and the resonant
frequency
is
proportional
to
(ft
3
b5
)
1/2
where f is the volume fraction of
BM fibers.
b) Fluid
The BM is mainly covered with soft cells that are in contact with extra-cellular fluid.
For the effect of the mass on the pressure distribution, there is little difference between
fluid, soft cells or a gel. As demonstrated by Békésy (1960, p. 445) in an experimental
model there is no change in localization when the fluid is replaced by gel. Consequently,
for modeling, the soft cells are often replaced by fluid. Both have similar acoustical
properties. The motion of an inviscid, incompressible fluid (or gel) is governed by the
well-known Laplace’s equation:
! 2" ! 2"
+
=0
!2 y !2 z
(Eq. 10)
in which ! is the displacement potential. The z-displacement and pressure are:
!"
w=
!z
# 2$
pF = ! "F 2
#t
(Eq. 11)
The solution giving the compatible displacement with the plate (Eq. 7) is:
28
W j# t " nz
e
sin ny
n
!="
(Eq. 12)
which gives the ratio of pressure to velocity:
pF
"#
= ! F = j "F# teffective
v
in
t effective =
1
= b /!
n
(Eq. 13)
Thus the inviscid, incompressible fluid has only the effect of a mass attached to the
plate, with the effective thickness t effective , about a third of the plate width b. Soft cells or a
gel, representing the organ of Corti, also satisfy the same equation, so Eq. 13 holds for
the fluid consisting of a thin or thick layer of soft cells and fluid. The difference between
the fluid with and without cells attached to the plate lies in the viscous correction, not the
effective mass.
c) Plate and fluid
Equating the impedance of the plate (Eq. 9) to the impedance of the fluid (Eq. 13)
gives the resonant frequency:
!2 =
Dn4 + Tn2
"P tP + 2 "F n
(Eq. 14)
Helmholtz (1868) proposed that the transverse fibers of the BM behaved as strings
under tension in air, as in a harp. This corresponds to setting the bending stiffness D and
the fluid inertia !F to zero in Eq. 14. A sketch of this is in Figure 9 and the result for the
first resonant frequency is:
frequencyTension
1" T %
= $
2 # !P tb2 '&
1/ 2
(Eq. 15)
However, there is not much evidence for high tension in the BM and the density of the
surrounding fluid is nearly the same as the BM. Consequently, the plate density term in
Eq. 14 is negligible. Setting the tension T and the plate density !P to zero in Eq. 14 gives
the resonant frequency:
frequency Bending
1 # Dn5 &
=
2! %$ 2 "F ('
1/ 2
1 # E! 5 &
=
2! %$ 24 "F ('
1/ 2
# ft 3 &
% b5 (
$
'
1/ 2
(Eq. 16)
With the BM dimensions and density of fibers (Cabezudo 1978) Eq. 16 provides a
reasonable frequency range for several mammals (Steele and Zais 1983). The formula
also works for recent measurements of the gerbil (Emadi et al. 2004). The wide
frequency bandwidth capability for the bending (Eq. 16) compared to the tension (Eq. 15)
is shown in Table 4. With a nominal Young’s modulus of elasticity for collagen, the
frequencies computed from Eq. 16 are close to the range for the guinea pig. In contrast, a
variation of tension by 104 would be required for the tension model to work, which is not
29
justified by the modest change in the dimensions of the BM support. Shown in Table 4 is
the width g of the spiral ligament. The tension is assumed to be proportional to g, and the
tension frequency is set equal to the bending frequency at the apex for comparison. The
conclusion is that it is bending stiffness that determines the frequency localization on the
BM.
Table 4. Frequency range capability of BM pectinate zone (for guinea pig) for bending
stiffness and tension stiffness.
Elastic modulus E
BM fiber vol fract f
BM width b
BM thickness t
Spiral ligament
width g
Frequency tension
Frequency bending
Base
1 GPa
0.08
80 µm
7 µm
200 µm
247 Hz
52,000 Hz
Apex
1 GPa
0.01
180 µm
1 µm
40 µm
Ratio
1
7
0.44
7
5
130 Hz
130 Hz
1.9
400
3. Vestibular fluid pressure to BM displacement
The equations for the slow wave, (Figure 7) in the model with symmetric SV and ST
without Reissner’s membrane (e.g., Peterson and Bogert 1950; Zwislocki 1953) can be
written as:
!
!2
( Ap ) = " #F 2 Q
!x
!t
(Eq. 17)
!
1
Q = "#A = "
2 pBM
!x
K Vol
(Eq. 18)
The distance along the BM from the stapes is x, the average pressure in SV is p , the
pressure acting on the BM is pBM , the volume displacement of fluid in SV is Q, the area
of SV is A(x), and the area displacement of the partition is !A = bw . Equation 17 follows
directly Newton’s second law of motion (Eq. 1) while Eq. 18 is a statement about
conservation of mass in a segment of scalae. The equations above are valid for 1-D, 2-D
and 3-D description for the fluid flow by incorporating the dimensionality into the
pressure pBM acting on the BM.
a) One-dimensional (1-D) approximation
For long wavelengths, the pressure is nearly constant on the cross section, so the
approximation is pBM = p , and the system is a standard transmission line wave equation.
For a single frequency, with all variables changing with e j! t , this reduces to:
d2
( Ap ) + m 2 ( x, ! ) ( Ap ) = 0
2
dx
(Eq. 19)
30
where the coefficient is:
2 "! 2
m ( x, ! ) =
AK Vol ( x )
2
(Eq. 20)
which can be identified as the local wave number. The wavelength is proportional to the
reciprocal of the wave number. For the cochlea, K Vol decreases with distance from the
stapes, so m increases with distance, meaning that the wavelength becomes short.
Because of the simple interpretation, the 1-D approximation continues to be the most
widely used for cochlear modeling. Zwislocki (1953) and then later Dallos (1973)
provide the history of the development. To improve the results, damping and mass are
added to the stiffness, as in Eq. 2. However, these values have no physical basis, so this
must be considered as a phenomenological model. Another approach is to ignore the
physical basis completely and determine the complex wave number m ( x, ! ) from
measurements of BM displacement phase and amplitude, and the neural response, so that
Eq. 19 will produce the measured response. This is often used in studies of the function
of higher neural centers, for which a simple but reasonable input from the cochlea,
described by Eq. 19, is desired. Flanagan and Bird (1962) developed this approach using
Békésy’s post mortem measurements of the GP cochlear response. Of interest is their use
of the Hilbert transform to show that the measurements are consistent for a causal and
stable system. Zweig (1991) further developed the approach for the in vivo
measurements of Rhode (1971) in squirrel monkey and obtained self-consistent effective
BM impedance. Although the physical behavior is 3-D, the traveling wave can indeed be
described by an equation of the form Eq. 19. So the choice is to fit the wave number from
the measurements of the response or compute it from the actual stiffness and mass
properties of the BM with the 3-D fluid motion. Since measurements are difficult and
restricted, there is interest in improving and verifying the capability for the direct
calculation. De Boer (2006) provides a recent perspective on the issues.
b) Two-dimensional (2-D) approximation
To place the cochlear model on a physical basis, more details of the fluid motion must
be considered (Ranke 1950; Berkley and Lesser 1973; Neely 1981). When the
wavelength is short for large m, the 1-D approximation is not valid because the pressure
on the BM is much larger than the average pressure, as indicated in the measurements
(Figure 8). The 2-D approximation (from Laplace’s equation in the x–z plane) is:
! 1
pBM
mH
=
!"
p
Tanh ( mH ) # mH
for
for
mH < 1 long wavelength
mH > 1 short wavelength
(Eq. 21)
in which H is the height of SV. With this, Eq. 19 is the same, but the wave number is:
2 !" 2
mH
m =
AK Vol ( x ) Tanh ( mH )
2
(Eq. 22)
For the square SV, A = H2, and this can be rewritten as:
31
2 !" 2
,
mHTanh ( mH ) =
K Vol ( x )
(Eq. 23)
which has the approximation:
)# 2 ! " 2 & 1/2
F
+%
+$ K Vol ( x ) ('
mH ! *
2
+ 2 ! F"
+ K ( x)
Vol
,
for
mH < 1 long wavelength
(Eq. 24)
for
mH > 1 short wavelength
Thus in the long wavelength region, the wave number is proportional to the frequency,
which is the characteristic of non-dispersive waves. For the short wavelength region, the
wave number is quadratic with the frequency, which indicates dispersion. At the point of
“partition resonance” defined by Eq. 16, this has the value:
mH !
8
!
(partition "resonance")
(Eq. 25)
A dimensionless form of Eq. 23 is:
m! =
8 "! 2
! Tanhm!
(Eq. 26)
in which
m! = mH ,
!! = ! / ! ref , ! ref
$ 8 K vol '
=&
% " 2#F )(
1/2
,
x! = xH .
The behavior indicated in the sketch of the slow wave in Figure 7 comes from Eq. 23.
Near the stapes, where x is small, the stiffness is large, so the wave number is small, i.e.,
the wavelength is long. As x increases, the wave number increases. The short wavelength
region begins when mH = 1, after which the wave number increases more rapidly. A little
past the beginning of the short wavelength region mH reaches the value shown in Eq. 25.
So when the fluid–elastic behavior is considered, Eq. 16 is seen to be a transition point at
which the wavelength really becomes short, rather than any local “resonance” similar to
the strings of a harp. When the wavelength becomes rather short, the damping due to the
fluid viscosity increases exponentially. It is therefore only a rough approximation to the
actual BF. When the fluid viscosity increases, the BF shifts to the base, and when the
cross-sectional area A of the scalae decreases, the BF shifts to the apex, with a less rapid
decay of the amplitude (Lim 2000).
c) Three-dimensional (3-D) model and viscosity
The extension to the 3-D analysis of the fluid, including the effect of viscosity, is
straightforward but tedious. The pressure at the basilar membrane of the 3-D fluid is
included by making pBM in Eq. 21 a function of not just scalae height H, but also the
scalae width W. Since the first development (Steele and Taber 1979), several authors
have used various approaches. Advances include the proof that Eq. 19 is valid for 3-D
32
without any assumption on the form of the solution; only the dispersion relation of Eq. 23
is modified (Baker 2000; Lim 2000; Lim and Steele 2002). The viscosity of the fluid adds
imaginary components to Eq. 23, so the wave number m becomes complex. Incorporation
of the 3-D fluid becomes critical for capturing both the magnitude and phase behaviour of
basilar membrane response with physical parameters (Kolston 2000).
d) Validation with physical modeling
A comparison of the 1-D, 2-D and 3-D calculations is shown in Figure 11. For this
calculation only the physical properties of fluid and partition measured by Helle are used.
The gain in accuracy with 3-D is well worth the slight extra effort of calculating the wave
number m from the 3-D generalization of Eq. 23. For the 1-D model to have the correct
BF, either the stiffness or mass must be modified from the physical value by a substantial
amount.
Figure 11: Amplitude of BM for
frequency 848 Hz in an experimental
model (Helle 1974). This is a box model
of the cochlea, six times human size,
with an isotropic polymeric BM. The
measured points are shown by ! . The
computations from 1-D, 2-D, and 3-D
approximations show that the 3-D
captures the behavior best (Steele and
Taber
1979).
Helle
measured
all
properties, so there are no free
parameters.
In recent times, several laboratories have used micromachining to obtain life-sized box
models of the cochlea. Traveling waves are found in models with fluid of the viscosity of
saline for (1) fluid on one side and the partition stiffness dominated by tension (White
and Grosh 2005) and (2) fluid on both sides and the stiffness dominated by bending with
9000 ribs to simulate the orthotropic construction in the real cochlea (Wittbrodt et al.
2006). In the latter work, each of four different membrane thicknesses yields reasonable
agreement between the calculation from the physical properties and the frequency
localization from the 3-D “WKB” calculation discussed in the next section. So finally
there is solid evidence that the 3-D fluid motion in the cochlea is captured properly by the
transmission line Eq. 19 with the 3-D determination of wave number.
4. Solution methods
With the advances in computing power, a direct finite difference computation for the
full 3-D cochlea is appealing. The problem is in the dimensions. With the typical cochlear
length 30 times the width, and the BM only 1/10 of the width, and the fluid viscous
boundary layer 1/10 of the width of the BM, a fixed mesh requires millions of degrees of
freedom. Therefore, even full use of parallel processing (Givelberg and Bunn 2003)
requires many hours of computing time for limited results for a linear model, that did
have the advantage of being coiled and with viscosity of the fluid. Kiefer, et al. (2006)
offer the model closest to the actual geometry of the human cochlea with the full 3-D
33
coiling. However, they use inviscid fluid, which greatly reduces the computing challenge.
In comparison, the 1-D model Eq. 19 can be solved by a variety of numerical methods.
Most efficient is an asymptotic method often referred to as “WKB”. For this, the solution
of Eq. 19 is written as:
j ! t " # x,!
Ap ! P ( x, ! ) e ( ( ))
(Eq. 27)
in which P ( x, ! ) is the “amplitude” function, and the exponential term provides the
traveling wave with the phase given by
! ( x, " ) =
# m ( x," ) dx
x
(Eq. 28)
0
The viscosity of the fluid contributes a negative imaginary part of the wave number m,
which causes the exponential decrease in amplitude of the traveling wave in the short
wavelength region. This approach was first used by Ranke (1950) on a 2-D model for the
cochlea. The viscous boundary layer of fluid adds an additional term to Eq. 26:
8
"! 2
m! =
(Eq. 29)
#1/2
! Tanhm! # 1 + j"$
! / m! 2
(
)
in which the viscosity parameter is:
! = " ref H 2 #F / µ .
The viscosity of the fluid is µ . Generally, the term ! is large, so the expansion for the
wave number is:
m! !
)
8"! 2 &
8"! 3/2
1
+
1
$
j
(
)
(
1/2 + ...+
# '
# ( 2% )
*
(Eq. 30)
which shows that the fluid viscosity adds to the effective mass with the positive real part
of the correction term, and provides the damping with the negative imaginary part. The
damping is small for !! < 1 but becomes significant for !! > 1 , causing the rapid high
frequency decay in amplitude.
A comparison of the 3-D calculation and measurements in the chinchilla is in Figure
12. The BM displacement is divided by the stapes displacement, so a linear system would
have the response independent of input amplitude. This is not the case for frequencies
near the maximum. However, for amplitudes greater than 80 dB SPL, the responses
converge, indicating a linear passive behavior, described well by Eq. 19 with the 3-D
extension of Eq. 22. Particularly note the phase in Figure 12(b), which corresponds to Eq.
24, linear in frequency for low frequency and quadratic in frequency for frequency
approaching BF and higher. This clearly shows the transition of wavelength from long to
short near BF. The phase has some dependence on amplitude near BF, but is remarkably
insensitive considering the huge change in the amplitude of the input sound.
34
Figure 12(a): Amplitude of BM
displacement measured in
chinchilla (Ruggero et al.
1997) and computed with 3-D
model with saturating feed
forward
(Lim
and
Steele
2002).
The
amplitude
is
normalized to the stapes
displacement.
Experimental
points are shown for 20 and
80 dB SPL. The active process
increases
the
relative
amplitude for low input sound
levels.
Figure 12(b): Phase relative to
the stapes velocity of BM
displacement
measured
(Ruggero et al. 1997) and
computed (Lim and Steele
2002), corrected by Y.J. Yoon.
The
phase
is
generally
insensitive to amplitude. For
low frequency, the phase is
nearly linear with frequency
(long
wavelength
1-D).
Approaching BF (10 kHz), the
phase
becomes
quadratic,
reflecting the dispersive 3-D
behavior.
A third region that appears in the BM measurements but not in the neural response is
the plateau in amplitude and phase just beginning at 13 kHz in Figure 12a. This is yet to
receive an explanation, but some consider this as evidence for the existence of additional
waves. There may well be more than just the fast and a slow wave shown in Figure 7.
The form of Eq. 27 is also convenient for transients, since the energy for the wave of a
given frequency arrives from the stapes at the point x in the time given by:
t arr ( x, ! ) =
"
"
# ( x, ! ) =
"!
"!
$ m ( x,! ) dx
x
0
(Eq. 31)
This approximation can be used to estimate the neural delay (Anderson et al. 1971). Thus
from Figure 12(b) the low frequencies have a constant low slope of phase, indicating a
fast arrival independent of frequency. For higher frequencies, the slope increases in
magnitude, indicating an increasingly longer time of arrival at this point and a dispersion
of the signal. Note that the slopes depend on the location along the cochlea. We note that
the passive cochlea is a causal and stable system. Eq. 31 is the group delay of the transfer
function relating the response at a point to the input at the stapes.
An important attribute of the auditory system is high frequency resolution of auditory
neurons (Kiang et al. 1965). The source of the high resolution, measured as bandwidth of
the response from the peak, is in the basilar membrane response (Narayan et al. 1998).
The sharp frequency resolution helps reject noise outside the bandwidth of interest for a
specific neuron. Thus the sharp resolution is important for increasing the signal-to-noise
35
ratio, particularly at low levels. It is well accepted that the bandwidth of the basilar
membrane increases as the level increases (Rhode 1971, see Figure 12) and this is now
believed to be due to non-linearity in the organ of Corti mechanics. Many consider this
due to the active process that is significant at low levels. For high levels the BM
response is linear and described well by the mechanics of the passive box model.
F. Organ of Corti – Fluid pressure to neural excitation
The inner ear provides the neural excitation for acousto-mechanical stimuli. Key to this
are receptor cells (hair cells), which transduce mechanical force on cilia (hairs) on one
end of the cell into increased firing of neurons via synapses near the other end. (See
chapter 2.) The hearing organs provides the sensation for the higher frequencies needed
for sound localization and speech reception. Man has an upper frequency of 20 kHz,
while some bats and toothed whales extend to over 150 kHz. As discussed in the previous
section, the box model of the cochlea, consisting only of fluid and BM, results in the
localizing of the BM displacement and fluid pressure to a certain region for a certain
frequency. In the cochlea, the organ of Corti (OC) is attached to the BM and contains the
receptor cells. This is the additional system needed to transfer the BM displacement to
force delivered to the cilia. In addition, the OC provides an active input of energy into
the traveling wave for low sound levels, which greatly increases the sensitivity and
frequency resolution of the basilar membrane displacement and neural excitation.
In non-mammalian vertebrates, receptor cells achieve much of their frequency
selectivity through the operation of electrical resonance. The ion channels in the
basolateral membrane of each cell constitute a miniature electrical circuit that tunes the
cell to a specific frequency of mechanical input. However, the mammalian OHC has the
unique property of high frequency electromotility, defined as a change in the cell length
in response to a change in the electric potential difference across the cell membrane
(Brownell et al. 1985). The potential difference across the cell membrane is the result of
intracellular voltage depolarization due to ion flow in the stereocilia. Ion channels in the
stereocilia are mechanically opened when there is displacement of the bundle in the
excitatory direction. The mechanical opening of the ion channels in the inner ear is
significantly faster than the cascade of chemical signals required for example in the
retina. Therefore, while the sensory receptor hair cells are all mechano-receptive in the
three types of organs in the inner ear, the means for accomplishing their excitation for
hearing are much more elaborate. Consequently, the cochlea remains more mysterious
than the vestibular system on many levels. As a small example, the most striking
geometric feature of coiling of the mammalian cochlea has yet to be adequately
explained. Packaging is certainly a consideration. However, West (1985) finds
correlation between hearing and coiling in land animals, while Cai et al. (2005) compute
the low frequency mechanical effects of coiling and in current work find remarkable
correlation of coiling and hearing in sea mammals.
1. Multi-scale organ of Corti model
The modeling of the OC with the inclusion of more complete anatomical details has
received increasing attention in recent years. Kolston (1999) developed the first detailed
model, in which the components of the OC are simplified to a rectangular grid and the
fluid viscosity neglected. He obtained the traveling waves in a significant length of the
36
cochlea. The calculation is by the finite element method (FEM), which is now the
prevalent method for structures and for fluid-structure interaction. Cai et al. (2004) and
Andoh and Wada (2004) use this to consider more realistic geometry for the cross
section, but use an approximation for the effect of the longitudinal motion, which is
significant for higher frequencies. Another approach is to calculate the stiffness
properties of the components of the OC first, and then incorporate the fluid motion in the
various compartments of the OC. The components are shown in Figure 13 (Steele and
Puria 2005).
It is safe to say that the complete solution for the transformation of the basilar
membrane motion to hair cell excitation for entire cochlea with a reasonable
representation for the OC for all frequencies of excitation is yet to be attained. In the
sections that follow, an approach to understanding the complex transduction that takes
place in the organ of Corti is presented. The model is based on known anatomy and
known material properties with assumptions about the method of feed-forward of outer
hair cell force for active amplification. In another chapter of this handbook, Neely and
Kim summarize other methods for active amplification that have been proposed.
Figure 13. Shell model for
guinea pig apex (y–z
plane). The dashed lines
show
the
undeformed
configuration, while the
solid
lines
show
the
deformed
configuration
due to static pressure
loading toward ST, greatly
amplified. The radial and
axial distances are in mm.
The labels are: SV scala
vestibule,
ST
scala
tympani, IS inner sulcus, C
Cortilymph, TM tectorial
membrane, IP inner pillar,
OP outer pillar, BM basilar
membrane, IHC inner hair
cells, OHC outer hair cells,
HS Hensen’s stripe, and L1
sub-tectorial
membrane
fluid region.
2. Outer hair cell motility: push-pull of BM
Many features of the geometry of the OC have been made clear from detailed
measurements in the guinea pig and by a large physical model (Voldrich and Ulehlova
1987). The inclination of the OHC in the radial cross section is evident in Figures 13 and
14. The inclination in the longitudinal direction is shown in Figure 14. The synaptic end
of the OHC is supported by Deiters’ cell. Each cell has an intracellular axial column
consisting of microtubules, referred to as Deiter’s rod in Figure 14. One end of the rod
cups the end of the OHC and the other end is attached to the BM. The Deiter’s rod
provides the dominant axial stiffness of the cell. In birds and other non-mammals there is
no motility and no stiff connection between the receptor cells and the BM. The cup of
37
Deiter’s rod at the synaptic end of the OHC also has an attachment to the reticular lamina
(RL) with a phalangeal process, shown in Figure 14. The process also consists of
microtubules. Thus the triangular arrangement of OHC, RL and Deiters’ process provides
a frame of significant elastic stiffness. The OHC is motile (Chapter 10), so a shear of the
cilia in the direction to cause hyper-polarization of the cell causes an expansion of the cell,
which causes a push down on the BM through the rod. The interesting feature is that the
shear on the cilia at the distance from the stapes given by x causes a push on the BM at
the distance x + !x .
Generally an active system with sensors and actuators that deliver energy to the
system, which affects the input-output relation, is called “feedback”. For a system
consisting of an input and output connected by a chain of processes, a sensor at one point
that causes actuation at a preceding point in the chain, is called “feed-backward”, while a
sensor that causes actuation at a subsequent point in the chain is called “feed-forward”.
The structure of the OC, shown in Figure 14 is elastic with the multiple attachments, so
the elongation of a single OHC causes a ripple effect of loading of the BM in both
directions. DeBoer and Nuttall (2003) use a novel approach and take this into account
with an array of impedances at different distances. The amplitudes of these feed-forward
and feed-backward elements are computed for a best fit with the experimental
measurements of BM response, using the 3-D calculation for the fluid. Here we offer a
direct physical interpretation of a simpler version.
Another feature is that the fibers of the BM are in a sandwich in the pectinate zone
(PZ), then flatten to one layer in the arcuate zone (AZ) between the outer pillar (OP) and
the inner pillar (IP). Since the bending stiffness D of a plate depends on the cube of the
thickness, the BM AZ has roughly 1/27 of the stiffness of the PZ. Thus the OP offers
significant support of the BM. Consequently, a simple model is the following sequence:
•
•
•
•
A downward pressure on the PZ, consisting of a positive fluid pressure in SV pF
and an effective pressure from the Deiters’ rods pR causes a shear force on the OP
foot of magnitude ( 2 pF + pR ) b / 2 at the distance x from the stapes.
The shear on the OP foot is roughly equal to the shear on the OHC cilia, if the
details of the OC fluid-elastic motion are ignored.
The shear is in the inhibitory direction and causes expansion of the OHC.
The tendency of the OHC to expand causes a compressive force in Deiters’ rods,
which is a downward force on the BM represented by the effective pressure pR .
However, this occurs at the distance x + !x . An equal and opposite force acts upward
on the RL. Since this is more compliant, the displacement is more than for the BM, as
shown in measurements in the cochlea and by calculations with the model in Figure 13.
This upward displacement of the RL causes a tension in the phalangeal process, and an
upward pull of the Deiters’ rod. The equation for this is:
pR ( x + !x,t ) = " #$ 2 pF ( x,t ) + pR ( x,t ) %& ' " 2 #$ 2 pF ( x + !x2 ,t ) + pR ( x + !x2 ,t ) %&
(Eq. 32)
Thus the rod at the point x + Δx is compressed by the OHC whose apex is at the point x
38
by an amount proportional to the total pressure on the membrane, fluid plus rod, at x. So
this is a positive “feed-forward” with the amplitude α. The rod is also pulled by the
phalangeal process by an amount proportional to the total pressure on the membrane at
point x + Δx2. So this is a negative “feed-backward”.
Figure 14: Side view of OHC
showing the inclination (x–z
plane). The end is supported by
the cup of Deiters’ cell, which has
a
rod
providing
mechanical
attachment to the BM and a
phalangeal
process
providing
attachment to the RL. Inward
shear of the stereocilia at the
point x causes hyperpolarization
of the OHC, which causes an
elongation of the OHC, resulting
in upward displacement of the RL
and downward displacement of
the BM. Because of the OHC
inclination, this is a downward
push on the Deiters’ rod at the
point x +Δx , “feed-forward”.
Because of the inclination of the
phalangeal process, this rod will
be
pulled
upward
by
an
elongation of the OHC at the
point x +Δ x2 which is a negative
“feed-backward”. The horizontal
projection of OHC plus process is
Δx2 .
If the solution is used in the form Eq. 27 with the assumption that Δx2 and Δx are small,
then Eq. 32 becomes:
pR e! jm"x = # [ 2 pF + pR ] ! # 2 [ 2 pF + pR ] e! jm"x2
(Eq. 33)
with which the rod pressure pR can be written in terms of the fluid pressure, so the total
pressure becomes:
2 pF + pR =
2 pF
1 ! "e
jm#x
+ " 2 e! jm ( #x2 ! #x )
(Eq. 34)
Adding this feed-forward and feed-backward to the previous Eq. 29 for the dimensionless
wave number yields:
m! =
8
! % tanh m! # 1 + j"$
! / m! 2
&
(
"! 2
#1/2
!
! x
+ ) 2 e# jm ( *!x2 # *!x ) '(
) '( %&1 # ) e jm*!
(Eq. 35)
Expanding this for small values as for Eq. 30 gives the real and imaginary parts:
39
! !
Re( m)
*
8 2'
1 8 2
#! )1 +
#! + % & % 2 ,
! "
"
2#$
)(
,+
(Eq. 36)
2
1
% 8 ! 2( . 1
! ! "' $ * 0
Im( m)
" ,-x! " , 2 ( -x! 2 " -x! ) 3
& # ) 0/ 2$+
!
32
(Eq. 37)
Thus the feed-forward and negative feed-backward tend to cancel in the real part.
However, the positive feed-forward and the negative feed-backward add to decrease the
damping due to the fluid viscosity. In calculations it is far better to use the complete
relation Eq. 35 and solve for the wave number iteratively. Results from this are shown in
Figure 15. The real part of m! , the spatial integral of which gives the phase, is not
sensitive to the values for the parameters. However, the imaginary part of m! has
dramatically different behavior. For the passive case, with both feed-forward and feedbackward set to zero, the fluid viscosity provides the only damping. This is rather
negligible for frequencies less than BF, ( !! < 1 ) but increases rapidly for higher
frequencies, and gives the rapid high frequency decay in Figure 12a. When feed-forward
is turned on with α = 0.08, Eq. 37 shows that the damping is decreased, but the full
solution in Figure 15 shows that the imaginary part of m! actually is positive for a range
of frequencies above BF. This can be interpreted as a negative damping due to the input
of energy from the OHC motility. When the negative feed-backward is added, the
positive range of the imaginary part of m! is decreased and sharpened.
With the approximation Eq. 32, the details of the OC can be neglected and the
transmission line model Eq. 19 used. The effect is just a modification in the BM volume
stiffness:
(
K Vol (x)!"
" K Vol (x) 1 # $ (x)e jm( x,% )&x + $ 2 (x)e# jm( x,% )( &x2 # &x )
)
(Eq. 38)
Near CF, the change in impedance is due to an apical shift in resonance for the lowlevel active case, but the phase change is small (Yoon et al. 2006). This indicates that the
zero crossings of the time domain response for the high level passive case and the low
level active case will be nearly invariant. This suggests that force generation by OHCs in
the feed-forward formalism satisfies the near-invariance of fine time structure of the
organ of Corti response predicted by Shera (2001).
The modification of BM stiffness is also valid in 1-D approximation (Eq. 20) and the
2-D formulation (Eq. 23) with the caveat that the stiffness may not be physical as
discussed above. Thus the feed-forward causes a decrease in the effective partition
stiffness and a negative damping. This is significant in the short wavelength region and
corresponds to a significant input of energy into the traveling wave. For very short
wavelength, however, the fluid viscosity dominates.
The results for the 1-D model for α2 = 0 (Geisler and Sang 1995) are excellent. The
motility of the OHC saturates, which is represented by multiplying the factor α with a
saturating function dependent on amplitude. The result for the dependence of the BM
amplitude on input sound amplitude for the 3-D model of the chinchilla cochlea is in
Figure 12. The simulation results compare very well with other experimental
40
measurements, capturing several nonlinear features observed in basilar membrane
responses. These include compression of response with stimulus level, two-tone
suppressions, and generation of harmonic distortion and distortion products (Lim and
Steele 2002). Transient click response has also been considered (Lim and Steele 2003).
The simulation results exhibit some of the characteristic nonlinear behavior of the basilar
membrane commonly observed in experimental measurements, such as significant
amplification and sustained "ringing" in the transient response at low stimulus level. The
simple feed-forward mechanism is able to capture the properties of the active process in
the cochlea without a second filter or resonance. All parameters are biologically based,
with the feed-forward needing only the inclination of the cells, assumed to be 30°, and
the maximum value of α taken as 0.35 for the 3-D calculation, which is modest.
a)
b)
! as a function of frequency !! from Eq. 35. The curves “FF + FB” are for the
Figure 15: Wave number m
feed-forward due to the OHC inclination and the negative feed-backward due to the reverse
! = 10 5 , !!x = 0.02 , !x! 2 = 0.07 ! = 0.08 ,
! 2 = 0.02 . The curves “FF” are with the effect of the feed-backward set to zero, ! 2 = 0 . The curves
“passive” are for both active effects turned off, ! 2 = 0 and ! = 0 . Finally the curves “reverse FF” are
x = "0.02 and ! 2 = 0 . (a) The real part
for the traveling wave moving toward the stapes with !!
! > 1 and little sensitivity to feed-forward or feed-backward. (b) The
shows rapid accumulation for !
inclination of the phalangeal processes, with parameters
imaginary part provides the effective damping of the wave, which is highly sensitive. The feedforward push of the OHC causes a region of positive values, i.e., negative damping. The addition of the
feed-backward “pull” of the phalangeal processes increases and sharpens the negative damping. For a
wave in the reverse direction, the damping is increased by both effects. So the forward and backward
waves are not the same.
The advantage of the distributed feed-forward system should be appreciated. All the
sensors and actuators are turned on, without the need for a “Maxwell’s demon” to turn on
the amplification where it is needed (Shera and Guinan 1999). For the long wavelength
region, it has the effect of a small shift in the stiffness of the partition, but near BF, the
negative damping is turned on with amplification of the signal of 40 dB or more. Then
past BF there is little effect, and the high frequency fall off is the same as for the passive
(Figure 12a). The assumption is that the OHC motility functions cycle by cycle without
41
restriction on frequency, i.e., α is independent of frequency. Whether the OHC actually
performs this is a subject of current investigation in several laboratories.
3. Time delay vs. feed-forward
Similar to deBoer and Nuttall (2003) we ask for the time delay that would have the
same effect as the spatial feed-forward and feed-backward. With a time delay Δt in the
pressure delivered to the BM from the OHC, Eq. 32 is replaced by:
pR ( x,t + !t ) = " #$ 2 pF ( x,t ) + pR ( x,t ) %&
(Eq. 39)
The wave number-frequency relation Eq. 35 is then:
m! =
8
"! 2
! % Tanhm! # 1 + j"$
! / m! 2
&
(
)
#1/2
(Eq. 40)
' %1 # ) e# j"!*t! '
(
(&
in which the dimensionless time delay is !t! = " ref !t . Expanding the wave number for
small β and !! > 1 as for Eq. 35 gives the real and imaginary parts:
! !
Re( m)
*
8 2'
1 8 2
#! )1 +
#! + % cos #! &t! , ,
! "
"
2#$
)(
,+
( 1 8 2
+
8
! ! " $! 2 *
Im( m)
$! + & sin $! 't! ! #
#
*) 2$%
-,
.
(Eq. 41)
(Eq. 42)
Since β is positive, a small time delay increases the damping. The time delay must be
“tuned” with !t! > " for a decrease in the damping that corresponds to an energy input
to the wave around BF !! " 1 . Another possibility is to make !t! < 0 , to obtain negative
damping for small time delay without tuning. However, this is a noncausal event, since
what occurs at future time is having an effect at present time, as pointed out by DeBoer
and Nuttall (2003) with a different approach.
The stability can be examined by considering, not a cochlea, but a simpler system
consisting of a tube with constant properties over a finite length with zero condition at the
end x! = L! . The solution Eq. 27, with forward and backward waves provides the transfer
function relating pressure at the general point x! to the input pressure at x! = 0:
!x
p ( x! ) e! jm!
! e B( )
=
!
!
p (0)
1 ! e! jm! B L ! jm! L
jm!
x! ! L! ! jm! L!
(Eq. 43)
where mB is the wave-number for the backward traveling wave, defined by Eq. 35 with
the signs of Δx and Δx2 changed. The poles are the zeros of the denominator at:
m! + m! B = 2k! / L!
(Eq. 44)
in which k is an integer. For each k, this equation may be solved for the complex
frequency. If the imaginary part of the frequency is negative, the solution is unstable in
time. Remarkably, the feed-forward and feed-backward terms tend to cancel in the
imaginary part, as can be seen by substituting the expansions Eqs. 36 and 37 into Eq. 44.
42
Direct numerical calculations for the solution of Eq. 44 support this, so it appears that the
spatial delay expressed by the feed-forward and feed-backward provides a stable system.
Even when the imaginary part of the wave number is positive, as shown in Figure 15, the
system remains stable. There is a limit to this, since for the gains ! " ! 2 # 1 , the
stiffness becomes zero for small frequency. A precise determination of the stability
boundaries has not been carried out, but the gains used in Figure 15 can be increased by a
factor of 3.9 until instability occurs. The zeros of the transfer function are the zeros of the
numerator at:
(
m! + m! B = 2k! / L! " x!
)
(Eq. 45)
which also have positive imaginary parts. So within certain limits, the feed-forward
system with a substantial gain in amplitude is stable and causal. This can be extended to
the cochlea with variable properties. The condition Eq. 44 becomes
L
! ( m + m )dx = 2k"
B
(Eq. 46)
0
which is more difficult to compute, but clearly with the same features.
In contrast, the forward and backward wave numbers are the same for the time delay
system. Consequently, the solutions of Eq. 39 show instability in time when the
imaginary part Eq. 42 is positive. Generally, feedback models incorporating time delay
require additional components to prevent undesirable behavior. The measurements of
Frank, et al. (1999) show no time delay between the motile force and transmembrane
potential. Therefore it appears most plausible that the frame structure in Figure 14 is for
the purpose of the feed-forward and negative feed-backward of energy into the traveling
wave. Information on the exact inclination of the OHC and phalangeal process is lacking,
but micrographs usually show a configuration similar to Figure 14. The one careful
examination of this is from Karavitaki (2002), who finds in gerbil that the RL is nearly
perpendicular to the OHC. Thus Δx is nearly zero. However, the Δx2 is apparently equal to
several OHC diameters, so the push-pull system works well.
4. Inner hair cell excitation
In the preceding discussion an approximate relation Eq. 40 is extracted from the
physics of the OC, leaving only a modification of the BM model. Subsequently the
details of the OC are avoided. However, the purpose of the OC is to provide the proper
excitation of the inner hair cells (IHC). The IHC cilia are not attached to the overlying
tectorial membrane and are subject to the mechanical force of the fluid motion, which is
dependent on the response of the entire structure of the OC. Consequently, the modeling
of the OC is the subject of numerous recent studies. Böhnke and Arnold (1998) provide
the most detailed FEM model, but without fluid. Kolston (1999) has inviscid fluid but
with geometric simplification of the OC structure. Hubbard, et al. (2003), Grosh et al.
(2004), and Mountain and Hubbard (2006) use other geometric simplifications. Cai and
Chadwick (2002), Andoh and Wada (2004), and Steele and Puria (2005) use detailed
FEM models with realistic geometry and stiffness properties for the components.
As discussed by these authors, there is growing awareness that the flow of the fluid in
the regions of the OC is important. Billone and Raynor (1973) provide perhaps the first
43
careful analysis of the flow around the IHC cilia. One must keep in mind that in the
hearing organ in lizards, there is considerable variety but always a group of receptor cells
without a TM and with tall cilia free in the fluid. Freeman and Weiss (1990) have
extensively investigated the mechanical behavior of these cilia through the relevant
frequency range (1 – 3 kHz). It is of interest that the neural tuning and otoacoustic
emissions from these receptor cells are similar to mammalian for the same frequency
(Manley 2006), without the TM, OHC motility, Deiter’s cells, etc, that seem to be so
important for mammals. For mammals a feature recently established by Edge et al. (1998)
is the proximity of the Hensen stripe, a protrusion of the tectorial membrane, to the tip of
the IHC cilia, as indicated in Figure 15.
Nowotny and Gummer (2006) provide a breakthrough with measurements of the lower
surface of the TM and the upper surface of the RL during electrical stimulation. They
find that these surfaces do not remain parallel, as usually assumed. The calculation for the
full elastic structure shows this as well. As can be seen in Figure 13, the region L1, near
the IHC cilia between the TM and RL opens with displacement of the BM toward ST.
This tends to pull fluid in from the IS past the IHC cilia. Just how much depends on the
relative stiffness of the TM and the proximity of the HS. Putting this together gives the
effects on the phase of IHC excitation given in Table 5. The phase measured in neurons
from the IHC in the middle and upper turns typically show for low frequency something
close to Case 2, with a change toward Case 1 as frequency increases (Cheatham and
Dallos 1999). In the base with a relatively stiffer TM, Ruggero et al. (2000) report values
similar to Cases 3 and 4.
Table 5 – Effects on phase of IHC tip link tension for BM motion toward ST, for
which the pillar head and base of cilium move radially outward. Cases 1 and 2
prevail for soft TM, while Cases 3 and 4 prevail for stiff TM.
Case
Cause
1
Small gap with HS (or high
frequency), cilium nearly
sticks to HS
Large gap with HS and TM
(or lower frequency),
cilium is pulled through
fluid
Small gap with HS, area of
region L1 increases, cilium
nearly sticks to HS, so L1
has negative pressure
Large gap with HS, area of
region L1 increases, so
fluid flows from IS into L1
2
3
4
Mechanism
Effect on IHC
neurons
Phase
Tip lags the base, causing
decrease in tip link tension in
phase with BM displacement
Tip lags the base, causing
decrease in tip link tension in
phase with BM velocity
Inhibition
0°
Inhibition
90°
Outward pressure on cilium,
causing increase in tip link
tension in phase with BM
displacement
Outward pressure on cilium,
causing increase in tip link
tension in phase with BM
velocity
Excitation
180°
Excitation
270°
44
Figure 16. Close view of IHC
cilia for guinea pig apex.
The Hensen stripe (HS) is
the triangle attached to the
tectorial membrane above.
The dashed lines show the
undeformed configuration,
with the tip of the IHC cilia
near the HS. The solid lines
show
the
deformed
configuration due to static
pressure loading toward ST,
greatly amplified. The radial
and axial distances are in
mm.
A strong mechanical nonlinearity comes from the restricted flow between the cilia,
tectorial membrane and Hensen stripe (Steele and Puria 2005). A result for this is in
Figure 17, which shows the tension in the tip link compared to the driving pressure,
positive in ST. Two peaks of the tension occur in each cycle of the pressure for a pressure
level corresponding to around 90 dB SPL. For lower sound pressure, the peak out of
phase with the pressure dominates, and for higher sound pressure only the peak in phase
with the pressure remains. This is remarkably close to the behavior of auditory neurons
sometimes observed (Kiang 1990).
A common expectation is that velocity of the BM toward ST will cause the IHC cilia to
be swept by the fluid in the inhibitory direction (to the left in Figure 13). However, it
seems that almost any phase of excitation is possible, depending on the specific geometry
and relative stiffness properties. In the static response shown in Figure 13, the subtectorial fluid region L1 is seen to open with BM displacement toward ST. This will
cause a fluid flow into L1 from the inner sulcus (IS) that will bend the cilia in the
excitatory direction. BM motion toward SV then is inhibitory. However, as the amplitude
increases, the tall cilia are constrained by the Hensen stripe while the RL still moves to
the left in Figure 13. This causes tension in the tip links seen as the in-phase peak in
Figure 17.
Figure 17: Nonlinear solution for the
force in the tip link at the guinea pig
base at 100 Hz. Around 90 dB SPL, two
peaks of force (nonlinear curve) occur
per cycle of ST pressure (cosine curve).
This offers a possible explanation for
the 180° change in phase and peak
splitting
sometimes
observed
in
auditory nerve fibers (Kiang 1990).
45
G. Summary of some issues
Rapid development in measurement and computational technique related to auditory
biomechanics is ongoing. Perhaps the following issues soon will be completely resolved.
1. Motion of tympanic membrane for high frequency
The simple model for middle ear has the tympanic membrane acting as a rigid,
massless piston. However, instead of piston behavior, surface displacement
measurements revealed multiple modes of vibration for frequencies above a few kHz
(Tonndorf and Khanna 1972). This has provoked considerable discussion. A recent
explanation offered in a preceding section is that the nonsymmetic material and
geometric properties of the membrane provide “mistuning” without strong resonances.
The consequence is a fairly uniform transmission of the pressure for the entire frequency
range without the need for woofer or tweeter. Full validation for this notion is in
progress.
2. Motion of ossicular chain for high frequency
The nonmammalian vertebrates have a simple columella that transmits the tympanic
membrane motion to the inner ear. In contrast the mammals have the three-bone ossicular
chain. In the simple model, this is represented by a simple lever with fixed pivot point.
However, measurements show that this is not the behavior for frequencies above a few
kHz (Decraemer, et al. 2003). The pivot point depends on frequency and the stapes
wobbles, instead of directly providing a volume displacement of the cochlear fluid. The
expectation is that this somehow permits the extension of the frequency range, but an
explanation is totally lacking.
3. Bone conduction
Hearing by bone conduction is of high clinical significance. There are many
measurements showing that the volume displacements of oval and round window are
exactly out of phase for air conducted acoustic excitation, consistent with the two modes
shown in Figure 7. All existing theory indicates that this is also the case for boneconducted sound. However, measurements by Stenfeld et al. (2004) indicate that this is
not the case for bone conduction. Indeed for some frequencies, the two windows are in
phase. Thus there must be compliance in the cochlea not yet explained (often referred to
as a “third window”). Dehiscence of the semi-circular canals has been clinically shown to
produce a third window (Chien et al. 2007; Merchant et al. 2007; Minor et al. 2003).
Sohmer and Freeman (2004) demonstrate that bone vibration generates acoustic pressure
in the brain that can generate auditory response. Estimates on the flow properties of the
cochlear and vestibular aqueducts indicate that the compliance is too low to offer a
reasonable acoustic pathway. Again an explanation is totally lacking.
4. Traveling wave
The traveling wave observed in the GP cochlea by Békésy (1960) was not anticipated
by any theoretical consideration. There remain contrary opinions, e.g., Sohmer and
Freeman (2004) consider their measurements as evidence against the existence of the
traveling wave. The traveling wave does not occur in lizards and turtles, but most likely
46
occurs in bird. For mammals, the evidence for the existence of the traveling wave seems
overwhelming. We mention the direct in vivo observation of waves by Ren (2002), the
close relation of BM displacement and neural excitation found in the same animal by
Narayan et al. (1998), and the agreement in theory with the traveling wave and
experiment for the BM motion (Figure 12). This disagreement should be at an end.
5. Motility vs. beating
In non-mammalian hearing organs, there are no arches of Corti, Deiter’s cells, nor
inner sulcus as shown in Figure 13. Furthermore the cells similar to the OHC’s cannot
have somatic motility. Nevertheless, in the responsive frequency range, the neural tuning
is as sharp as in mammals, and evoked and spontaneous emissions occur very similar to
those in mammals (Manley 2006). Crawford and Fettiplace (1985) discovered that the
cilia on turtle hair cells have spontaneous activity, i.e., they beat without external
excitation. This mechanotransducer (MET) channel phenomenon is described as a Hopf
bifurcation (Choe, et al. 1998). In all vertebrates, the cilia and transduction channels are
similar. Is the energy of the active process generated by MET instability or somatic
motility of the cell, or is it a combination? This is a subject of current investigation (e.g.,
Chan and Hudspeth 2005). Frank et al. (1999), discovered that the ratio of OHC motile
force to transmembrane voltage remains constant to nearly 100 kHz without time delay,
which supports the notion that motility is a unique feature of the OHC and must be
important for mammalian hearing. Indeed the recent results on rat cochleas by Kennedy
et al. (2006) offer evidence that both MET resonance and somatic motility are
interacting.
6. OHC roll off
The feed-forward (and negative feed-backward) discussed here depends on the force of
motility of the OHC to be independent of frequency. However, the electrical properties of
the OHC appear to be such that for a fixed amplitude of shear force on the cilia, there is a
significant decrease in the intracellular potential at a frequency much less than the BF.
Several laboratories propose more detailed analysis of intracellular or extracellular
behavior that would maintain the effect of the motility for high frequency. Without a
more elaborate cell model, Baker (2000) and Grosh et al. (2004) use models with correct
physical values for the electrical and mechanical properties of the OHC, but with
resonant TM, and find that the effect of the motility for high frequency is preserved.
7. TM properties- resonant TM?
Many authors have used OC models with a strong resonance of the TM (e.g., Allen
1980). Several laboratories have measured the properties of the TM, most recently Gueta
et al. (2006) and Masaki et al. (2006). Details are different, but the general conclusion is
that the TM is rather soft tissue, with an elastic Young’s modulus in the range 0.5 – 30
kPa. Zwicker (1972) points out that squirrel monkey and pig have a great difference in
TM size. Such a difference for animals that have roughly the same frequency range makes
a resonant TM seem unlikely. Nowotny and Gummer (2006) measure the TM response
due to electrical stimulation and find no resonance for frequencies through BF. So there
47
are indications that the TM does not have a strong resonance.
8. Multiple traveling wave modes
The common box model has the fast and slow waves indicted in Figure 7. However,
each of the fluid spaces in the OC (Figure 13) can support an independent wave.
Karavitaki (2002) offers measurements of motion of the OC that support the notion of
multiple waves. As discussed by deBoer (2006) recent models, e.g., Zhang et al. (1997)
and Mountain and Hubbard (2006), have such capability. The goal remains for a model
of the OC with physically realistic geometric and stiffness properties and with 3-D
viscous fluid, that can simulate the environment of the cilia for all frequencies. The
expectation is that waves in the IS and tunnel space do play a significant role.
9. Stiffness change along the cochlea
Almost every component of the cochlear cross section has at one time or another been
proposed as the fundamental resonance element. Most probably agree with Békésy
(1960) that the BM has the strongest stiffness gradient and is the most likely candidate.
The calculation in Table 4 shows that the modest variation in values of width, thickness,
and fiber volume fraction of the pectinate zone work together to explain the frequency
range of the GP cochlea. The change in the volume stiffness is five orders of magnitude.
However, the direct measurement of the GP cochlea by Békésy (1960) shows a change of
three orders of magnitude, with a reasonable extrapolation to four orders of magnitude.
Similarly, Zhang et al. (1997) find that the point load stiffness variation is inadequate to
explain the frequency range in gerbil. With a different preparation, however, Emadi et al.
(2004) find much more compliance in the apical region, which seems to fit the theoretical
values from the geometry. The conclusion is that the soft cells covering the BM make
point load or volume compliance measurements difficult to interpret. As is often the case,
a combination of theoretical and experimental approaches is needed.
H. General summary
There are many acoustical and mechanical transformations performed by outer ear,
middle ear and cochlear structures. The components in the mammalian ear are more
elaborate than those in non-mammalian vertebrates, with the advantage of a subsequently
extended frequency range. The anatomically intricate complexity of the mammalian ear
ultimately results in greater functional capabilities. Some of quantifiable variables are
sensitivity, frequency bandwidth, frequency resolution, dynamic range and sound
localization. The structures that lead to these capabilities do so given the available
biological materials, space constraints within the skull, and limitations imposed by
biophysics.
Several fundamental biophysical principles provide the means for obtaining the proper
mechanical forcing of receptor cells in the inner ear. Each of the transformation steps can
be described by a basic principle that can be readily understood using computational
biomechanics. The objective of each transformation is to preserve the sound relevant to
the species for the stated functionality. Each implementation is, however, much more
complicated and involves biomechanical principles that are not all well characterized, yet
48
to be implemented in any man-made device, and not free from controversy.
Less controversial is the spatially dependent transformation of sound by the pinna and
the ear canal. The next step is the impedance alleviation between the air and fluid of the
cochlea, which requires an area change provided by the eardrum to stapes footplate. It is
not possible to have a rigid, massless piston for this, so the tympanic membrane is an
elaborate vibrating system with mistuning of the different radial sectors, each with
significant resonances for frequencies over about 2 kHz. The ensemble, however, delivers
a fairly smooth pressure to the ossicular chain. In the ossicular chain, the principle of a
lever advantage is also readily grasped, but the chain does not behave as a simple lever
for higher frequencies (> 2kHz). An adequate understanding of how the pressure is
transmitted to the cochlea is yet to be attained.
In the cochlea, the local “resonance” at BF is easily calculated for the BM immersed in
fluid and soft cells. The reality of transmission of the pressure to this point involves the
fast wave and the slow traveling wave, with its long and short wavelengths. The BF is not
really a resonance in the sense of a set of tuned strings, but rather a point of transition to
very short wavelengths. The actual BF location depends on fluid viscosity, width of the
partition with respect to the BM, and sound level. The enhancement of the traveling wave
by the active process for low levels of sound remains a subject of contention. The
simplest model of feed-forward provided by the geometry and the motility of the OHC
appears to explain much. Such a distributed system of sensors and actuators is effective
in enhancing the BM response near BF. Finally, the transformation from BM motion to
excitation of the IHC has the simple explanation of cilia being dragged through fluid. The
details of the environment of the cilia and the proximity of the Hensen stripe make the
actual cilia-fluid response much more complicated. Calculations for low frequency have a
resemblance to measurements in IHC and in the neurons of the auditory nerve. However
the full effect of the complex geometry for the full range of frequency and amplitude is
yet to be examined. It is safe to predict that other mechanical design features are present
in the OC to obtain the proper excitation of the IHC, which are not yet anticipated. The
interplay between physiological measurements and bio-computational models helps to
elucidate the knowns from the unknowns and thus provides a path towards greater
understanding.
49
Acknowledgements
Many thanks to Gerald Popelka, Stefan Heller, and to the editor Peter Dallos for
helpful comments and suggestions on earlier drafts. This work was supported in part by
grant R01 DC 05960 from the National Institute of Deafness and other Communication
Disorders of the National Institutes of Health and by grant RGP0051 from the Human
Frontiers of Science Program.
50
Bibliography
Aibara, R., J. T. Welsh, S. Puria and R. L. Goode (2001). "Human middle-ear sound
transfer function and cochlear input impedance." Hear Res 152(1-2): 100-9.
Algazi, V. R., R. O. Duda, R. Duralswami, N. A. Gumerov and Z. Tang (2002).
"Approximating the head-related transfer function using simple geometric models
of the head and torso." J Acoust Soc Am 112(5 Pt 1): 2053-64.
Algazi, V. R., R. O. Duda, D. M. Thompson and C. Avendano (2001). "The CIPIC HRTF
database." Applications of Signal Processing to Audio and Acoustics, 2001 IEEE
Workshop, New Paltz, NY
Allen, J. B. (1980). "Cochlear micromechanics--a physical model of transduction." J
Acoust Soc Am 68(6): 1660-70.
Allen, J. B. and S. T. Neely (1992). "Micromechanical models of the cochlea." Physics
Today 45: 40-47.
Anderson, D. J., J. E. Rose, J. E. Hind and J. F. Brugge (1971). "Temporal position of
discharges in single auditory nerve fibers within the cycle of a sine-wave
stimulus: frequency and intensity effects." J Acoust Soc Am 49(4): Suppl
2:1131+.
Andoh, M. and H. Wada (2004). "Prediction of the characteristics of two types of
pressure waves in the cochlea: theoretical considerations." J Acoust Soc Am
116(1): 417-25.
Baker, G. J. (2000). Pressure-feedforward and piezoelectric amplification models for the
cochlea. Ph.D. Thesis, Stanford University.
Beer, H. J., M. Bornitz, H. J. Hardtke, R. Schmidt, G. Hofmann, U. Vogel, T. Zahnert
and K. B. Huttenbrink (1999). "Modelling of components of the human middle
ear and simulation of their dynamic behaviour." Audiol Neurootol 4(3-4): 156-62.
Berkley, D. A. and M. B. Lesser (1973). "Comparison of single- and double-chamber
models of the cochlea." J Acoust Soc Am 53(4): 1037-8.
Billone, M. and S. Raynor (1973). "Transmission of radial shear forces to cochlear hair
cells." J Acoust Soc Am 54(5): 1143-56.
Boer, E. de (1991). "Auditory physics. Physical principles in hearing theory. III." Physics
Reports 203(3): 125-231.
Boer, E. de (2006). "Cochlear activity in perspective." , Auditory Mechanisms, Processes
and Models, Eds. A. L. Nuttall, T. Ren, P. Gillespie, K. Grosh and E. de Boer
(Portland, OR, World Scientific). 393-409
Boer, E. de and A. L. Nuttall (2003). "Properties of amplifying elements in the cochlea."
Biophysics of the Cochlea, Ed. A. W. Gummer (World Scientific). 331-342
Bohnke, F. and W. Arnold (1998). "Nonlinear mechanics of the organ of Corti caused by
Deiters cells." IEEE Trans Biomed Eng 45(10): 1227-33.
Brandt, J. F. and H. Hollien (1967). "Underwater hearing thresholds in man." J. Acoust.
Soc. Am. 42(5): 966-971.
Brownell, W. E., C. R. Bader, D. Bertrand and Y. de Ribaupierre (1985). "Evoked
mechanical responses of isolated cochlear outer hair cells." Science 227(4683):
194-6.
51
Békésy, G. (1952). "Direct observation of the vibrations of the cochlear partition under a
microscope." Acta Otolaryngol 42(3): 197-201.
Békésy, G. v. (1960). Experiments in hearing. New York, AIP Press.
Cabezudo, L. M. (1978). "The ultrastructure of the basilar membrane in the cat." Acta
Otolaryngol Suppl 86: 160-175.
Cai, H. and R. Chadwick (2002). "Radial structure of traveling waves in the inner ear."
SIAM Journal on Applied Mathematics 63(4): 1105-20.
Cai, H., D. Manoussaki and R. Chadwick (2005). "Effects of coiling on the
micromechanics of the mammalian cochlea." J R Soc Interface 2(4): 341-8.
Cai, H., B. Shoelson and R. S. Chadwick (2004). "Evidence of tectorial membrane radial
motion in a propagating mode of a complex cochlear model." Proc Natl Acad Sci
U S A 101(16): 6243-8.
Chan, D. K. and A. J. Hudspeth (2005). "Mechanical responses of the organ of Corti to
acoustic and electrical stimulation in vitro." Biophys J 89(6): 4382-95.
Cheatham, M. A. and P. Dallos (1999). "Response phase: a view from the inner hair
cell." J Acoust Soc Am 105(2 Pt 1): 799-810.
Chien, W., M. E. Ravicz, J. J. Rosowski and S. N. Merchant (2007). "Measurements of
Human Middle- and Inner-Ear Mechanics With Dehiscence of the Superior
Semicircular Canal." Otol Neurotol 28(2): 250-257.
Corey, D. P. and A. J. Hudspeth (1983). "Kinetics of the receptor current in bullfrog
saccular hair cells." J Neurosci 3(5): 962-76.
Choe, Y , M.O. Magnasco, A.J. Hudspeth (1998). “A model for amplification of hairbundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction
channels”, Proc Natl Acad Sci U S A 95(26)15321-15326
Crawford, A. C. and R. Fettiplace (1985). "The mechanical properties of ciliary bundles
of turtle cochlear hair cells." J Physiol 364: 359-79.
Dalchow, C. V., A. L. Weber, S. Bien, N. Yanagihara and J. A. Werner (2006). "Value of
digital volume tomography in patients with conductive hearing loss." Eur Arch
Otorhinolaryngol 263(2): 92-9.
Dallos, P. (1973). The auditory periphery; biophysics and physiology. New York,
Academic Press.
Dancer, A. and R. Franke (1979). "Intracochlear acoustic pressure measurements in
guinea pigs." Scand Audiol Suppl(9): 111-7.
Dancer, A. and R. Franke (1980). "Intracochlear sound pressure measurements in guinea
pigs." Hear Res 2(3-4): 191-205.
Decraemer, W. and S. Khanna (1995). "Malleus vibration modelled as rigid body
motion." Acta Otorhinolaryngol Belg 49(2): 139-45.
Decraemer, W. F., J. J. Dirckx and W. R. Funnell (1991). "Shape and derived geometrical
parameters of the adult, human tympanic membrane measured with a phase-shift
moire interferometer." Hear Res 51(1): 107-21.
Decraemer, W. F., J. J. Dirckx and W. R. Funnell (2003). "Three-dimensional modelling
of the middle-ear ossicular chain using a commercial high-resolution X-ray CT
scanner." J Assoc Res Otolaryngol 4(2): 250-63.
Decraemer, W. F., S. M. Khanna and W. R. Funnell (1991). "Malleus vibration mode
changes with frequency." Hear Res 54(2): 305-18.
52
Decraemer, W. F., M. A. Maes and V. J. Vanhuyse (1980). "An elastic stress-strain
relation for soft biological tissues based on a structural model." J Biomech 13(6):
463-8.
DPA (2005). Sound and Divers, http://www.mod.uk/dpa/projects/sonarenvir/impact.htm
Eberl, D. F., G. M. Duyk and N. Perrimon (1997). "A genetic screen for mutations that
disrupt an auditory response in Drosophila melanogaster." Proc Natl Acad Sci U S
A 94(26): 14837-42.
Edge, R. M., B. N. Evans, M. Pearce, C. P. Richter, X. Hu and P. Dallos (1998).
"Morphology of the unfixed cochlea." Hear Res 124(1-2): 1-16.
Eiber, A. and H. G. Freitag (2002). "On Simulation models in otology." Multibody
System Dynamics 8(2): 197-217.
Eisner, E. (1967). "Complete Solutions of the "Webster" horn equations." J Acoust Soc
Am 41(4P2): 1126-1146.
Emadi, G., C. P. Richter and P. Dallos (2004). "Stiffness of the gerbil basilar membrane:
radial and longitudinal variations." J Neurophysiol 91(1): 474-88.
Fay, J., S. Puria, W. F. Decraemer and C. Steele (2005). "Three approaches for estimating
the elastic modulus of the tympanic membrane." J Biomech 38(9): 1807-15.
Fay, J. P. (2001). Cat Eardrum Mechanics. Ph.D. Thesis, Stanford University.
Fay, J. P., S. Puria and C. R. Steele (2006). "The discordant eardrum." Proc Natl Acad
Sci U S A 103(52): 19743-8.
Fay, R. R. (1988). Hearing in Vertebrates; a Psychophysics Databook. Winnetka,
Illinois, Hill-Fay Associates.
Flanagan, J. L., and C. M. Bird (1962). "Minimum phase response for the Basilar
Membrane." J Acoust Soc Am 34(1): 114-118.
Fleischer, G. (1978). "Evolutionary principles of the mammalian middle ear." Adv Anat
Embryol Cell Biol 55(5): 3-70.
Fleischer, G. (1982). "[Hearing mechanisms in dolphins and baleen whales (author's
transl)]." Hno 30(4): 123-30.
Frank, G., W. Hemmert and A. W. Gummer (1999). "Limiting dynamics of highfrequency electromechanical transduction of outer hair cells." Proc Natl Acad Sci
U S A 96(8): 4420-5.
Freeman, D. M. and T. F. Weiss (1990). "Hydrodynamic forces on hair bundles at high
frequencies." Hear Res 48(1-2): 31-6.
Funnell, W. R., W. F. Decraemer and S. M. Khanna (1987). "On the damped frequency
response of a finite-element model of the cat eardrum." J Acoust Soc Am 81(6):
1851-9.
Funnell, W. R., H. T. Shiah, M. D. McKee, S. J. Daniel and W. F. Decraemer (2005).
"On the coupling between the incus and the stapes in the cat." JARO 6(1): 9-18.
Gan, R. Z., B. Feng and Q. Sun (2004). "Three-dimensional finite element modeling of
human ear for sound transmission." Ann Biomed Eng 32(6): 847-59.
Geisler, C. D. and C. Sang (1995). "A cochlear model using feed-forward outer-hair-cell
forces." Hear Res 86(1-2): 132-46.
Givelberg, E. and J. Bunn (2003). "A comprehensive three-dimensional model of the
cochlea." Journal of Computational Physics 191(2): 377-391.
53
Goode, R. L., M. Killion, K. Nakamura and S. Nishihara (1994). "New knowledge about
the function of the human middle ear: development of an improved analog
model." Am J Otol 15(2): 145-54.
Gopfert, M. C. and D. Robert (2001). "Biomechanics. Turning the key on Drosophila
audition." Nature 411(6840): 908.
Grosh, K., J. Zheng, Y. Zou, E. de Boer and A. L. Nuttall (2004). "High-frequency
electromotile responses in the cochlea." J Acoust Soc Am 115(5 Pt 1): 2178-84.
Gueta, R., D. Barlam, R. Z. Shneck and I. Rousso (2006). "Measurement of the
mechanical properties of isolated tectorial membrane using atomic force
microscopy." Proc Natl Acad Sci U S A 103(40): 14790-5.
Guinan, J. J., Jr. and W. T. Peake (1967). "Middle-ear characteristics of anesthetized
cats." J. Acoust. Soc. Am. 41: 1237-1261.
Gundersen, T. and K. Høgmoen (1976). "Holographic vibration analysis of the ossicular
chain." Acta Otolaryngol. 82: 16-25.
Hecht, C., S. Shlaer, and M. H. Pirenne (1942). "Energy, quanta, and vision." The Journal
of General Physiology, 25: 819-840.
Helle, R. (1974). Beobachtungen an hydromechanischen Modellen des Innenohres mit
nachBuildung von Basilarmembran, Corti-Organ und Deckmembran, Ph.D.
Thesis, Technical University of Munich.
Helmholtz, H. L. F. (1868). Die Mechanik der Gehorknochelchen und des Trommelfells.
(M. Cohen und Sohn, Bonn).
Hemila, S., S. Nummela and T. Reuter (1999). "A model of the odontocete middle ear."
Hear Res 133(1-2): 82-97.
Henson, M. M., V. J. Madden, H. Rask-Andersen and O. W. Henson, Jr. (2005). "Smooth
muscle in the annulus fibrosus of the tympanic membrane in bats, rodents,
insectivores, and humans." Hear Res 200(1-2): 29-37.
Henson, O. W., Jr. and M. M. Henson (2000). "The tympanic membrane: highly
developed smooth muscle arrays in the annulus fibrosus of mustached bats." J
Assoc Res Otolaryngol 1(1): 25-32.
Hofman, P. M., J. G. Van Riswick and A. J. Van Opstal (1998). "Relearning sound
localization with new ears." Nat Neurosci 1(5): 417-21.
Howard, J. and A. J. Hudspeth (1988). "Compliance of the hair bundle associated with
gating of mechanoelectrical transduction channels in the bullfrog's saccular hair
cell." Neuron 1(3): 189-99.
Hubbard, A. E., D. C. Mountain and F. Chen (2003). "Time-domain responses for a
nonlinear sandwich model of the cochlea." Biophysics of the Cochlea, Ed. A.
Gummer (World Scientific). 315-330
Huttenbrink, K. B. (1988). "[Mechanics of the ear ossicles in static pressures. II. Impaired
joint function and surgical reconstruction of the ossicle chain]." Laryngol Rhinol
Otol (Stuttg) 67(3): 100-5.
Huttenbrink, K. B. (1989). "[The functional significance of the suspending ligaments of
the ear ossicle chain]." Laryngorhinootologie 68(3): 146-51.
Karavitaki, K. D. (2002). Measurements and models of electrically-evoked motion in the
gerbil organ of Corti. Ph.D. Thesis, Boston University.
54
Keefe, D. H., J. C. Bulen, K. H. Arehart and E. M. Burns (1993). "Ear-canal impedance
and reflection coefficient in human infants and adults." J Acoust Soc Am 94(5):
2617-38.
Kennedy, H. J., M. G. Evans, A. C. Crawford and R. Fettiplace (2006). "Depolarization
of cochlear outer hair cells evokes active hair bundle motion by two
mechanisms." J Neurosci 26(10): 2757-66.
Khanna, S. M. and J. Tonndorf (1969). "Middle ear power transfer." Arch Klin Exp
Ohren Nasen Kehlkopfheilkd 193(1): 78-88.
Khanna, S. M. and J. Tonndorf (1972). "Tympanic membrane vibrations in cats studied
by time-averaged holography." J Acoust Soc Am 51(6): 1904-20.
Kiang, N. Y. (1990). "Curious oddments of auditory-nerve studies." Hear Res 49(1-3): 116.
Kiang, N. Y. S., T. Watanabe, E. C. Thomas and L. F. Clark (1965). Discharge Patterns
of Single Fibers in the Cat’s Auditory Nerve. Cambridge, MA, MIT Press.
Kiefer, J., F. Bohnke, O. Adunka and W. Arnold (2006). "Representation of acoustic
signals in the human cochlea in presence of a cochlear implant electrode." Hear
Res 221(1-2): 36-43.
Koike, T., H. Wada and T. Kobayashi (2002). "Modeling of the human middle ear using
the finite-element method." J Acoust Soc Am 111(3): 1306-1317.
Kolston, P. J. (1999). "Comparing in vitro, in situ, and in vivo experimental data in a
three-dimensional model of mammalian cochlear mechanics." Proc Natl Acad Sci
U S A 96(7): 3676-81.
Kolston, P. J. (2000). "The importance of phase data and model dimensionality to
cochlear mechanics." Hear Res 145(1-2): 25-36.
Kuypers, L. C., W. F. Decraemer, J. J. Dirckx and J. P. Timmermans (2005). "Thickness
Distribution of Fresh Eardrums of Cat Obtained with Confocal Microscopy." J
Assoc Res Otolaryngol: 1-11.
Lim, D. J. (1995). "Structure and function of the tympanic membrane: a review." Acta
Otorhinolaryngol Belg 49(2): 101-15.
Lim, K. M. (2000). Physical and mathematical cochlear models. Ph.D. Thesis, Stanford
University.
Lim, K. M. and C. R. Steele (2002). "A three-dimensional nonlinear active cochlear
model analyzed by the WKB-numeric method." Hear Res 170(1-2): 190-205.
Lim, K. M. and C. R. Steele (2003). "Response suppression and transient behavior in a
nonlinear active cochlear model with feed-forward." International Journal of
Solids and Structures 40(19): 5097-5107.
Lynch, T. J., 3rd, V. Nedzelnitsky and W. T. Peake (1982). "Input impedance of the
cochlea in cat." J Acoust Soc Am 72(1): 108-30.
Lynch, T. J., 3rd, W. T. Peake and J. J. Rosowski (1994). "Measurements of the acoustic
input impedance of cat ears: 10 Hz to 20 kHz." J Acoust Soc Am 96(4): 2184209.
Magnan, P., P. Avan, A. Dancer, J. Smurzynski and R. Probst (1997). "Reverse middleear transfer function in the guinea pig measured with cubic difference tones."
Hear Res 107(1-2): 41-5.
55
Manley, G. A. (2006). "Spontaneous otoacoustic emissions from free-standing
stereovillar bundles of ten species of lizard with small papillae." Hear Res 212(12): 33-47.
Margolis, R. H. (1993). "Detection of hearing impairment with the acoustic stapedius
reflex." Ear Hear 14(1): 3-10.
Margolis, R. H. and G. R. Popelka (1975). "Loudness and the acoustic reflex." J Acoust
Soc Am 58(6): 1330-2.
Masaki, K., T. F. Weiss and D. M. Freeman (2006). "Poroelastic bulk properties of the
tectorial membrane measured with osmotic stress." Biophys J 91(6): 2356-70.
Merchant, S. N., M. E. Ravicz, S. Puria, S. E. Voss, K. R. Whittemore, Jr., W. T. Peake
and J. J. Rosowski (1997). "Analysis of middle ear mechanics and application to
diseased and reconstructed ears." Am J Otol 18(2): 139-54.
Merchant, S. N., J. J. Rosowski and M. J. McKenna (2007). "Superior semicircular canal
dehiscence mimicking otosclerotic hearing loss." Adv Otorhinolaryngol 65: 13745.
Michelsen, A. (1966). "Pitch discrimination in the locust ear: observations on single
sense cells." J Insect Physiol 12(9): 1119-31.
Minor, L. B., J. P. Carey, P. D. Cremer, L. R. Lustig, S. O. Streubel and M. J.
Ruckenstein (2003). "Dehiscence of bone overlying the superior canal as a cause
of apparent conductive hearing loss." Otol Neurotol 24(2): 270-8.
Mountain, D. C. and A. E. Hubbard (2006). "What stimulates the inner hair cell?",
Auditory Mechanisms, Processes and Models, Eds. A. L. Nuttall, T. Ren, P.
Gillespie, K. Grosh and E. de Boer (Portland, OR, World Scietific). 466-473
Murugasu, E., S. Puria and J. B. Roberson, Jr. (2005). "Malleus-to-footplate versus
malleus-to-stapes-head ossicular reconstruction prostheses: temporal bone
pressure gain measurements and clinical audiological data." Otol Neurotol 26(4):
572-82.
Møller, A.R. (1963). "On Transmission Characteristic of Middle Ear." Acta Physiologica
Scandinavica 59: 105-&.
Møller, A. R. (1961). "Network Model of Middle Ear." J Acoust Soc Am 33(2): 168-&.
Narayan, S. S., A. N. Temchin, A. Recio and M. A. Ruggero (1998). "Frequency tuning
of basilar membrane and auditory nerve fibers in the same cochleae." Science
282(5395): 1882-4.
Nedzelnitsky, V. (1980). "Sound pressures in the basal turn of the cat cochlea." J Acoust
Soc Am 68(6): 1676-89.
Neely, S. T. (1981). "Finite difference solution of a two-dimensional mathematical model
of the cochlea." J Acoust Soc Am 69(5): 1386-91.
Nobili, R., F. Mammano and J. Ashmore (1998). "How well do we understand the
cochlea?" Trends Neurosci 21(4): 159-67.
Nowotny, M. and A. W. Gummer (2006). "Nanomechanics of the subtectorial space
caused by electromechanics of cochlear outer hair cells." Proc Natl Acad Sci U S
A 103(7): 2120-5.
Nummela, S. (1995). "Scaling of the mammalian middle ear." Hear Res 85(1-2): 18-30.
Olson, E. S. (1998). "Observing middle and inner ear mechanics with novel intracochlear
pressure sensors." J. Acoust. Soc. Am. 103: 3445-3463.
56
Olson, E. S. (1998). "Observing middle and inner ear mechanics with novel intracochlear
pressure sensors." J Acoust Soc Am 103(6): 3445-63.
Onchi, Y. (1949). "A Study of the Mechanism of the Middle Ear." J Acoust Soc Am
21(4): 404-410.
Onchi, Y. (1961). "Mechanism of Middle Ear." J Acoust Soc Am 33(6): 794-&.
Pang, X. D. and J. J. Guinan, Jr. (1997). "Effects of stapedius-muscle contractions on the
masking of auditory-nerve responses." J Acoust Soc Am 102(6): 3576-86.
Perkins, R. C. (1980). "Laser stepedotomy for otosclerosis." Laryngoscope 90(2): 228-40.
Peterson, L. C. and B. P. Bogert (1950). "A Dynamical Theory of the Cochlea." J Acoust
Soc Am 22(3): 369-381.
Prendergast, P. J., P. Ferris, H. J. Rice and A. W. Blayney (1999). "Vibro-acoustic
modelling of the outer and middle ear using the finite-element method." Audiol
Neurootol 4(3-4): 185-91.
Puria, S. (2003). "Measurements of Human Middle Ear Forward and Reverse Acoustics:
Implications for Otoacoustic Emissions." J Acoust Soc Am 113(5): 2773-2789.
Puria, S. and J. B. Allen (1991). "A parametric study of cochlear input impedance." J
Acoust Soc Am 89(1): 287-309.
Puria, S. and J. B. Allen (1998). "Measurements and model of the cat middle ear:
evidence of tympanic membrane acoustic delay." J Acoust Soc Am 104(6): 346381.
Puria, S., L. D. Kunda, J. B. Roberson and R. C. Perkins (2005). "Malleus-to-footplate
ossicular reconstruction prosthesis positioning: Cochleovestibular pressure
optimization." Otology & Neurotology 26(3): 368-379.
Puria, S., W. T. Peake and J. J. Rosowski (1997). "Sound-pressure measurements in the
cochlear vestibule of human-cadaver ears." J Acoust Soc Am 101(5 Pt 1): 275470.
Puria, S., J. H. Sim, M. Shin, J. Tuck-Lee and C. R. Steele (2006). Middle ear
morphometry from cadaveric temporal bone microCT imaging. Middle Ear
Mechanics in Research and Otology. Eds. A. Eiber and A. Huber. Zurich, SW,
World Scientific.
Rabbitt, R. D. and M. H. Holmes (1986). "A fibrous dynamic continuum model of the
tympanic membrane." J. Acoust. Soc. Am. 80(6): 1716-1728.
Ranke, O. (1950). "Theory of operation of the cochlea: a contribution to the
hydrodynamics of the cochlea." J Acoust Soc Am 22(6): 772-777.
Ren, T. (2002). "Longitudinal pattern of basilar membrane vibration in the sensitive
cochlea." Proc Natl Acad Sci U S A 99(26): 17101-6.
Rhode, W. S. (1971). "Observations of the vibration of the basilar membrane in squirrel
monkeys using the Mossbauer technique." J Acoust Soc Am 49(4): Suppl
2:1218+.
Rosowski, J. J. and S. N. Merchant (1995). "Mechanical and Acoustic Analysis of
Middle-Ear Reconstruction." American Journal of Otology 16(4): 486-497.
Rosowski, J. J., J. E. Songer, H. H. Nakajima, K. M. Brinsko and S. N. Merchant (2004).
"Clinical, experimental, and theoretical investigations of the effect of superior
semicircular canal dehiscence on hearing mechanisms." Otol Neurotol 25(3): 32332.
57
Ruggero, M. A., S. S. Narayan, A. N. Temchin and A. Recio (2000). "Mechanical bases
of frequency tuning and neural excitation at the base of the cochlea: comparison
of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla."
Proc Natl Acad Sci U S A 97(22): 11744-50.
Ruggero, M. A., N. C. Rich, A. Recio, S. S. Narayan and L. Robles (1997). "Basilarmembrane responses to tones at the base of the chinchilla cochlea." J Acoust Soc
Am 101(4): 2151-63.
Shaw, E. A. (1974). "Transformation of sound pressure level from the free field to the
eardrum in the horizontal plane." J Acoust Soc Am 56(6): 1848-61.
Shaw, E. A. and R. Teranishi (1968). "Sound pressure generated in an external-ear
replica and real human ears by a nearby point source." J Acoust Soc Am 44(1):
240-9.
Shera, C. A. (2001). "Intensity-invariance of fine time structure in basilar-membrane
click responses: implications for cochlear mechanics." J Acoust Soc Am 110(1):
332-48.
Shera, C. A. and J. J. Guinan, Jr. (1999). "Evoked otoacoustic emissions arise by two
fundamentally different mechanisms: a taxonomy for mammalian OAEs." J
Acoust Soc Am 105(2 Pt 1): 782-98.
Shera, C. A. and G. Zweig (1991). "Asymmetry suppresses the cochlear catastrophe." J
Acoust Soc Am 89(3): 1276-89.
Sim, J. H., S. Puria and C. R. Steele (2003). Three-Dimensional measurements and
analysis of the isolated malleus-incus complex. Middle Ear Mechanics in
Research and Otology. K. Gyo, H. Wada, N. Hato and T. Koike. (World
Scientific).
Simmons, F. B. and D. L. Beatty (1962). "A theory of middle ear muscle function at
moderate sound levels." Science 138: 590-2.
Sohmer, H. and S. Freeman (2004). "Further evidence for a fluid pathway during bone
conduction auditory stimulation." Hear Res 193(1-2): 105-10.
Steele, C. R. and S. Puria (2005). "Force on inner hair cell cilia." International Journal of
Solids and Structures 42(21-22): 5887-5904.
Steele, C. R. and K. R. Shad (1995). "Asymptotic-numeric solution for shells of
revolution." Applied Mechanics Reviews 48(11, part 2).
Steele, C. R. and L. A. Taber (1979). "Comparison of WKB calculations and
experimental results for three-dimensional cochlear models." J Acoust Soc Am
65(4): 1007-18.
Steele, C. R. and J. Zais (1983). Basilar membrane properties and cochlear response.
Mechanics of Hearing. E. a. V. de Boer, MA. Delft, Delft University Press: 29–
36.
Stenfelt, S., N. Hato and R. L. Goode (2004). "Fluid volume displacement at the oval and
round windows with air and bone conduction stimulation." J Acoust Soc Am
115(2): 797-812.
Stinson, M. R. and S. M. Khanna (1994). "Spatial distribution of sound pressure and
energy flow in the ear canals of cats." J. Acoust. Soc. Am. 96(1): 170-180.
Teranishi, R. and E. A. Shaw (1968). "External-ear acoustic models with simple
geometry." J Acoust Soc Am 44(1): 257-63.
58
Tonndorf, J. and S. M. Khanna (1972). "Tympanic--membrane vibrations in human
cadaver ears by time-averaged holography." J. Acoust. Soc. Am. 52: 1221-1233.
Voldrich, L. and L. Ulehlova (1987). "Cochlear micromechanics." Acta Otolaryngol
103(5-6): 661-4.
Wada, H. and T. Kobayashi (1990). "Dynamical behaviour of middle ear: Theoretical
study corresponding to measurement results obtained by a newly developed
measuring apparatus." J. Acoust. Soc. Am. 87(1): 237-245.
Wada, H., T. Metoki and T. Kobayashi (1992). "Analysis of dynamic behaviour of
human middle ear using a finite-element method." J. Acoust. Soc. Am. 92(2):
3157-3168.
Weiss, J. and J. Gardiner (2001). "Computational Modeling of Ligament Mechanics."
Critical Reviews in Biomedical Engineering 29(3): 1-70.
West, C. D. (1985). "The relationship of the spiral turns of the cochlea and the length of
the basilar membrane to the range of audible frequencies in ground dwelling
mammals." J Acoust Soc Am 77(3): 1091-101.
Wever, E. G. and M. Lawrence (1954). Physiological Acoustics, Princeton University
Press.
White, R. D. and K. Grosh (2005). "Microengineered hydromechanical cochlear model."
Proc Natl Acad Sci U S A 102(5): 1296-301.
Wiener, F. M., R. R. Pfeiffer and A. S. Backus (1966). "On the sound pressure
transformation by the head and auditory meatus of the cat." Acta Otolaryngol
61(3): 255-69.
Willi, U. B., M. A. Ferrazzini and A. M. Huber (2002). "The incudo-malleolar joint and
sound transmission losses." Hear Res 174(1-2): 32-44.
Windmill, J. F., M. C. Gopfert and D. Robert (2005). "Tympanal travelling waves in
migratory locusts." J Exp Biol 208(Pt 1): 157-68.
Wittbrodt, M. J., C. R. Steele and S. Puria (2006). "Developing a physical model of the
human cochlea using micro-fabrication methods." Audiology and Neurotology
11:104-112.
Yang, X. and O. W. Henson, Jr. (2002). "Smooth muscle in the annulus fibrosus of the
tympanic membrane: physiological effects on sound transmission in the gerbil."
Hear Res 164(1-2): 105-14.
Yoon, Y. J., S. Puria and C. R. Steele (2006). "Intracochlear pressure and organ of corti
impedance from a linear active three-dimensional model." ORL J
Otorhinolaryngol Relat Spec 68(6): 365-72.
Zhang, L., D. C. Mountain and A. E. Hubbard (1997). "Shape and stiffness changes of
the organ of Corti from base to apex cannot predict characteristic frequency
changes: are multiple modes the answer?" Conference In Name, World
Scientific). 472-478
Zweig, G. (1991). "Finding the impedance of the organ of Corti." J Acoust Soc Am
89(3): 1229-54.
Zwicker, E. (1972). "Investigation of the inner ear of the domestic pig and the squirrel
monkey with special regard to the hydrodynamics of the cochlear duct."
Symposium on Hearing Theory IPO, Eindhoven, Holland. 182-185
59
Zwislocki, J. (1948). "Theorie der Schneckenmechanik, qualitative und quantitative
Analyse [Theory of cochlear mechanics.]." Acta Oto-Laryngologica
72(Supplement): 1-76.
Zwislocki, J. (1961). "Acoustic measurement of the middle ear function." Ann Otol
Rhinol Laryngol 70: 599-606.
Zwislocki, J. (1963). "An Acoustic Method for Clinical Examination of the Ear." J
Speech Hear Res 13: 303-14.
Zwislocki, J. J. (1953). "Review of Recent Mathematical Theories of Cochlear
Dynamics." J Acoust Soc Am 25(4): 743-751.
Zwislocki, J. J. (1965). Analysis of some auditory characteristics. Handbook of
Mathematical Physiology. Luce, Bush and Galanter (Ed.). New York, Wiley: 346.
Zwislocki, J. J. (1975). "The role of the external and middle ear in sound transmission."
The Nerveous System. Vol. 3, Human Communication and its Disorders. D. B.
Tower (Ed.). New York, Raven Press: 44-55.
Choe, Y , M.O. Magnasco, A.J. Hudspeth (1998). “A model for amplification of hairbundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction channels”,
Proc Natl Acad Sci U S A 95(26)15321-15326
i
The work for the absolute threshold of hearing
-18
(p
2
)
/ !c " Area " Time is easiest to estimate at the
tympanic membrane and it is about 6x10 J for the energy for humans, using a threshold of hearing of p =
15 µPa (-3 dB SPL), pars tensa Area = 55 mm2, ! = 1.18 kg/m3, c = 344 m/s, Time = 0.2 sec. If we assume
that there is a loss of a factor of two between the middle ear and hair cell detectors, the threshold of hearing
becomes about 3x10-18 J.
60
ii
A dark-adopted eye requires 90 photons within 0.1 sec to perceive a flash. However, the estimate is that
only 10% of the photons entering the eye actually reach the cones, so that gives about 10 photons necessary
for the perception (Hecht, et al. 1942). The energy of a single photon in the middle of the visible spectrum
( !c / ! ) is 4x10
-19
J, using ! = 6.6 ! 10 Js , c = 3 ! 10 m/s , and ! = 500 " 10 m . Therefore, for 10
-34
8
-9
photons the energy is 4x10-18 J.
iii
It has been observed for some time that the threshold of hearing in subjects can has jumps in it. However,
the mechanism behind this behaviour is not well understood and may well be related to non-linear
properties of the cochlea at low level and internal reflections leading to standing waves.
iv
Here it is assumed that the middle ear cavity pressure at the round window is negligible which is the case
in normal ears. In pathological ears the pressure at the oval and round windows maybe more comparable,
due to acoustic coupling, and thus the important determining variable there is the pressure difference
between the two windows (Merchant et al., 1997).
v
The specific impedance was calculated as the measured cochlear input impedance Zc times the footplate
area. In humans the average magnitude of Zc is 21/2x21x109 kg/sec-m4 and the average footplate area is
3.21x10-6 m2 (Aibara et al. 2001). The 21/2 is to convert the peak velocity to rms velocity.
vi
The one exception to this is the recent finding that the concave-eared torrent frog species listen to mating
calls that are pres
vii
The reciprocal of this can is found in loudspeaker designs. If one takes an isolated loud-speaker (the
output driver) it would operate as a dipole generating nearly equal opposite signals from the two sides that
would tend to cancel in the far field. To increase the acoustic output of a speaker driver, it is almost always
placed in a cabinet that prevents cancellation from the opposite phase.
61