Download Modeling phase microscopy of transparent three

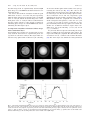
1268
J. Opt. Soc. Am. A / Vol. 26, No. 5 / May 2009
Sierra et al.
Modeling phase microscopy of transparent
three-dimensional objects: a
product-of-convolutions approach
Heidy Sierra,* Charles A. DiMarzio, and Dana H. Brooks
Electrical and Computer Engineering Department, Northeastern University, 360 Huntington Avenue,
Boston, Massachusetts 02115, USA
*Corresponding author: [email protected]
Received October 28, 2008; revised March 15, 2009; accepted March 22, 2009;
posted March 23, 2009 (Doc. ID 103197); published April 28, 2009
We present a product-of-convolutions (POC) model for phase microscopy images. The model was designed to
simulate phase images of thick heterogeneous transparent objects. The POC approach attempts to capture
phase delays along the optical axis by modeling the imaged object as a stack of parallel slices. The product of
two-dimensional convolutions between each slice and the appropriate slice of the point spread function is used
to represent the object at the image plane. The total electric field at the image plane is calculated as the product of the object function and the incident field. Phase images from forward models based on the first Born and
Rytov approximations are used for comparison. Computer simulations and measured images illustrate the
ability of the POC model to represent phase images from thick heterogeneous objects accurately, cases where
the first Born and Rytov models have well-known limitations. Finally, measured phase microscopy images of
mouse embryos are compared to those produced by the Born, Rytov, and POC models. Our comparisons show
that the POC model is capable of producing accurate representations of these more complex phase images.
© 2009 Optical Society of America
OCIS codes: 180.0180, 180.6900, 110.2990, 170.6900.
1. INTRODUCTION
Phase microscopy has been used extensively to acquire information about unstained transparent biological objects
[1–8]. These objects are visualized well by techniques
such as differential interference contrast (DIC) microscopy, but standard DIC systems are qualitative in nature
and do not provide quantitative phase information [9].
Several modalities have been developed to obtain quantitative complex field images of a sample, which can be
used to extract the amplitude and phase distribution of
the object [3–8,10,11]. Images acquired with these modalities can be interpreted easily when the imaged object is
optically thin, that is, when the thickness of the object is
much less than the depth of field of the imaging system.
However, many objects of interest are optically thick, with
thickness comparable to or larger than the depth of field
[12]. There are still many unanswered questions about
how three-dimensional (3D) structures affect phase images when imaging thick objects. It is therefore necessary
to develop techniques that help us understand the information that phase images provide about thick objects.
Considerable effort has been focused on the modeling
and characterization of microscope images to gain a better understanding of the underlying imaging systems and
to validate the resultant images. These methods have included both the use of linearized models and direct numerical approaches. Methods in the first group have been
based on the first Born and Rytov approximations
[13–17]. These models have the advantage that they are
well understood and simple to implement. However, the
Born and Rytov approximations place strong constraints
1084-7529/09/051268-9/$15.00
on the maximum size of the object and the refractive index contrast [18–20]. For example, Preza et al. in [14] defined a 3D model for DIC microscopy based on the first
Born approximation as an extension of an earlier twodimensional (2D) model [21]. This model works extremely
well with thin objects, but as the authors pointed out, the
model breaks down when the object is optically thick. In
[15], a 3D optical transfer function was presented based
on Streibl’s approach [16] for predicting 2D phase images
of a thick object. This method was applied for simulating
quantitative phase amplitude microscopy (QPAM) images
of thick objects. Such QPAM images are obtained by leveraging the changes introduced in intensity images with
small defocus. The phase image predictions were obtained
under the assumptions of the first Born approximation.
As noted, these approaches again worked well for thin objects, but have significant limitations when the objects
are optically thick or strongly heterogeneous. More complex algorithms have been proposed to handle the case of
thick objects including the generalized ray tracing approach [22], direct solutions to Maxwell’s equations [23],
and higher-order Born and Rytov approximations used in
tomography [24–27]. These methods usually require extensive numerical computations to simulate the required
volume at adequate resolution, and some of them cannot
be directly applied to phase microscopy systems. Therefore, for the purpose of studying phase microscopy systems and understanding the images of objects with varied
thickness, there remains a need for a more computationally tractable approach than full physical modeling.
In this work we describe such a model for transmission
© 2009 Optical Society of America
Sierra et al.
quantitative phase imaging, based on a product-ofconvolutions (POC) approach. The model is not more computationally intensive than those based on the first Born
and Rytov approximations, while relaxing the object size
and contrast limitations that those approximations impose. We compare the ability of the POC, Born, and Rytov
models to predict 2D phase images for a variety of thick
objects. Comparisons with both simulated and experimental images show that the POC approach provides a more
consistent representation of phase images for thick objects than first Born and Rytov approximation models.
The POC model treats the object volume as a stack of
thin parallel planes or slices normal to the optical axis. A
similar approach for modeling transparent objects for optical tomography was reported in [28,29], where a firstorder Taylor series was used to approximate the object.
When the total electric field was calculated at the image
plane, the Taylor series approximation reduced to the
first Born approximation, which assumes weak scatter
and small object thickness, thus making it inappropriate
for modeling thick objects. The POC approach does not require such an approximation for the object function.
Rather, the model explicitly represents an image of each
parallel object plane at the image plane. It calculates this
image of each plane via a 2D convolution between each
object slice and the corresponding slice of the point spread
function (PSF) that describes the system. The total object
image is then calculated as the product of these 2D convolutions for each object slice. Thus the object phase at
the image plane is the superposition of all the phases
from each parallel plane. The idea behind the slice image
multiplication in the POC model is to take into consideration the change in phase introduced along the optical
axis as light propagates through the object, rather than
treating each slice’s phase contribution additively in the
field, as in the Born and Rytov approximations. Because
they rely on adding each slice’s contribution to the image,
these models do not consider interactions between planes
that may include object thickness and phase information.
This difference allows the POC model to be less sensitive
to limitations on object thickness. However, like Born and
Rytov, POC neglects backscatter and relies on a discretization along the optical axis.
The split-step beam propagation method (BPM), also
known in the acoustic wave propagation modeling field as
the parabolic approximation [30–32], discretizes the optical axis just as the POC model does. The BPM introduces
changes in phase along the optical axis as light propagates through the object by multiplying fields, as the POC
method does. However the BPM operates at the object
plane; the incident field at each slice is propagated within
that slice using an impulse response and then is multiplied by the object’s contribution at that slice. This computation is carried out in a serial fashion through the object, thus propagating the field along the optical axis.
Because of the interslice multiplications, an additive
phase effect is achieved. Once the total object volume has
been covered, the field exiting the object is convolved with
the PSF of the optical system to propagate it to the image
plane. As a consequence of this approach, the diffraction
effect from the objective lens is introduced only once, operating on the whole object when calculating the final
Vol. 26, No. 5 / May 2009 / J. Opt. Soc. Am. A
1269
propagation to the image plane. On the other hand, the
POC model introduces the diffraction effect on each slice
independently when it is propagated to the image plane.
The total object representation is obtained as the product
of all propagated slices. Depending on the object geometry
and thickness, the BPM approach could introduce a phase
shift that may produce a phase wrapping effect along z if
changes in phase are larger than 2␲. This effect must be
considered in each slice, so that it does not affect calculation of the phase of the object. Since the propagation in
POC is done independently in the image plane, this phase
shift effect is already considered in the PSF of the system.
Beyond that, our preliminary simulations, not reported
here, indicate that there are some differences between the
POC and BPM methods in their ability to accurately represent sharp edges of optically thick objects, as well as
their relative sensitivity to arbitrary modeling decisions
such as the limits of the computational object volume. In
what follows we concentrate on the methods that have
been more commonly applied to phase microscopy, the linearized methods, and leave a careful comparison of the
BPM with POC to later work.
In this work we describe the formulation of the POC
model and show how it relates to the first Born and Rytov
approximations. We report results from both simulated
and experimental images of both homogeneous and heterogeneous objects to compare all three approaches. Our
results show that the POC model behaves similarly to the
Born and Rytov approximations when the object is thin,
but maintains an accurate representation of the phase
image as object thickness and index of refraction variations increase to the point where the Born and Rytov
models start to degrade.
The rest of the paper is arranged as follows. Section 2
describes the 3D object model used and then details the
use of this model to generate the images produced by the
POC approach and the first Born and Rytov approximations. Examples of data generated for 3D objects with
phase variations along the optical axis are presented in
Section 3. This section also provides a comparison between the simulated and measured data. Finally, Section
4 contains our conclusions and future work.
2. MODELING A PHASE MICROSCOPY
IMAGING SYSTEM
A. Three-Dimensional Transparent Object Model
As noted, we model 3D transparent objects as a stack of
parallel transparent slices. Each mth slice is defined in
terms of its index of refraction n共x , y , zm兲 and thickness
⌬z. A cartoon of our object representation is shown in Fig.
1. Observe that the illumination light propagates perpendicularly through each slice.
A similar object model was presented in [28,29]. In that
approach the object was also imaged in transmission
mode and refraction, reflection, and diffusion effects were
neglected. The object was described as a stack of translucent parallel slices and each slice was defined in terms of
the transmission and absorption coefficients.
In our approach, the 3D physical object is modeled optically in terms of the index of refraction alone. The index
of refraction within the object is expressed in the form
1270
J. Opt. Soc. Am. A / Vol. 26, No. 5 / May 2009
Sierra et al.
models provide an expression for the total electric field at
the image plane and will be presented using the PSF. We
will begin with a calculation of the perturbed field at the
image plane using the first Born approximation and then
define the first Rytov approximation at the image plane,
which is based on the perturbed field generated by the
first Born approximation.
Fig. 1. (Color online) Cartoon of 3D object description. The object is discretized along the optical axis and the light propagates
perpendicularly through each slice. For illustration, a section of
seven interior slices, each of thickness ⌬z, is shown expanded in
the bottom part of the figure.
n共x , y , z兲 ⬇ n0 + n␦共x , y , z兲, where n␦共x , y , z兲 is the difference
between the index of refraction of the object and the immersion medium n0. The optical behavior of every object
point is modeled by an exponential complex phase function f共x , y , z兲 = exp关jkn␦共x , y , z兲⌬z兴, where k = 2␲ / ␭ is the
wave vector in free space for wavelength ␭. As noted, absorption and backscatter are neglected.
B. Phase Microscopy Imaging Model
The imaging system model uses a simple optical system
approach as shown in Fig. 2. It is composed of a 3D object,
a light source, and a lens. The light source is modeled as a
coherent plane wave. The plane immediately preceding
the lens is referred to as the pupil plane. The image formation model is as follows: light propagates along the optical axis and interacts with the object. After this interaction, the transmitted light is spatially truncated in the
pupil plane to represent the finite extent of the imaging
lens, and the truncated light then propagates to the image plane.
This image formation process is modeled using a theoretical model of the PSF h共x , y , z兲. The PSF of an optical
system can be modeled in several different forms depending on the system used [16,17,33]. Since here we are interested in coherent transmission optical systems, the
PSF is based on Fresnel–Kirchhoff diffraction [34,35].
In the Subsections 2.B.1–2.B.3 we present a brief theoretical description of the first Born and Rytov approximations and then the details of the POC model. All three
1. First Born Approximation
The first Born approximation calculates the total electric
field as a superposition of the fields from all of the slices,
assuming there is no interaction between them [20]. It
models the total electric field at the image plane zI, as the
sum of an unperturbed incident field U0共x , y , zI兲, which is
the field that propagates through a homogeneous medium, and a perturbed field Up共x , y , zI兲 produced by the
heterogeneities in the medium,
U共x,y,zI兲 = U0共x,y,zI兲 + Up共x,y,zI兲.
The total electric field U共x , y , zm兲 incident at an object
plane zm is
U共x,y,zm兲 = U0共x,y,zm兲 + Up共x,y,zm兲,
共2兲
where Up共x , y , zm兲 corresponds to the perturbed field that
precedes zm. Thus, the expression for the propagated field
through an object slice with thickness ⌬z and location zm
is
U共x,y,zm + ⌬z兲 = 关U0共x,y,zm兲 + Up共x,y,zm兲兴
⫻exp关jkn␦共x,y,zm兲⌬z兴.
共3兲
The first Born approximation assumes an optically weak
object, which means 兩n␦共x , y , z兲兩 Ⰶ n0. Thus the perturbed
field is small when compared to the incident field and its
interaction with the preceding object slices can be neglected. Then the total field at zm + ⌬z can be expressed in
terms of the interaction of the unperturbed incident field
with the object slice function,
U共x,y,zm + ⌬z兲 ⬇ U0共x,y,zm兲exp关jkn␦共x,y,zm兲⌬z兴.
共4兲
The exponential object function can be expanded with a
first-order Taylor series approximation with respect to ⌬z
giving the following result:
U共x,y,zm + ⌬z兲 ⬇ U0共x,y,zm兲 + jkU0共x,y,zm兲n␦共x,y,zm兲⌬z,
共5兲
where jkU0共x , y , zm兲n␦共x , y , zm兲⌬z is the perturbed field
from the single slice between zm and zm + ⌬z. The perturbed field from the complete object at the image plane
Up共x , y , zI兲 is the coherent sum of the perturbed fields
from all of the slices through the object propagated to the
image plane. This perturbed field can be expressed as a
3D convolution between Up共x , y , z兲 and the PSF h共x , y , z兲
[14]. Thus the expression for the perturbed field at the image plane is
m=N
UB共x,y,zI兲 ⬇
兺
m=−N
Fig. 2. (Color online) Optical transmission system illustration.
The light is propagated to the image plane using a PSF model
defined in terms of the numerical aperture of the objective lens.
Coherent illumination is assumed.
共1兲
⌬z
冕冕
U0共x̃,ỹ,zm兲关jkn␦共x̃,ỹ,zm兲兴
r,s
⫻h共x − x̃,y − ỹ,zI − zm兲dx̃dỹ,
共6兲
where ⌬z is the thickness of each slice and r , s define the
Sierra et al.
Vol. 26, No. 5 / May 2009 / J. Opt. Soc. Am. A
intervals over which we consider the transverse coordinates 共x , y兲. The incident field at the image plane also can
be calculated using the PSF as follows:
U0共x,y,zI兲 =
冕冕
U0共x̃,ỹ,z0兲h共x − x̃,y − ỹ,zI − z0兲dx̃dỹ,
r,s
共7兲
U共x,y,zI兲 = exp关␾共x,y,zI兲兴,
N
U共x,y,zI兲 ⬇ U0共x,y,zI兲
兿
m=−N
冢
⌬z
1+
冕冕
冕冕
exp关jkn␦共x̃,ỹ,zm兲⌬z兴
共12兲
The POC model assumes that each g共x , y , zm ; zI兲 can be expressed as an exponential complex function:
g共x,y,zm ;zI兲 = exp关␾p⬘ 共x,y,zm ;zI兲兴.
U0共x,y,zI兲
共13兲
An expression for the total object phase at the image
plane is computed in terms of the phase of each object
slice as seen at the image plane. Therefore, from the as-
共9兲
,
where UB共x , y , zI兲 is the perturbed field calculated by the
first Born approximation. Thus, the total electric field at
the image plane can be obtained as
冉
U共x,y,zI兲 = U0共x,y,zI兲exp
UB共x,y,zI兲
U0共x,y,zI兲
冊
.
共10兲
Equation (10) leads to the Rytov approximation imaging
model,
U0共x,y,zI兲
r,s
⫻h共x − x̃,y − ỹ,zI − zm兲dx̃dỹ.
UB共x,y,zI兲
关U0共x̃,ỹ,zm兲共jkn␦共x̃,ỹ,zm兲兲h共x − x̃,y − ỹ,zI − zm兲兴dx̃dỹ
3. Product-of-Convolutions Model
The POC model defines the phase of the total electric field
at the image plane as the sum of the phase of the incident
field at the detector in the absence of the object ␾0共x , y , zI兲,
and the phase introduced by the object at the image plane
[36]. We will define this phase function as ␾p⬘ 共x , y , zI兲 to
differentiate it from the perturbed phase ␾p共x , y , zI兲 defined in Eq. (10) for the first Rytov approximation. For the
POC model, the complex phase function ␾p⬘ 共x , y , zI兲 is the
sum of the phase from each object slice after it is propagated to the image plane by a 2D convolution with the
PSF.
Let g共x , y , zm ; zI兲 be the representation at the image
plane for an object slice f共x , y , zm兲 located at the plane zm:
g共x,y,zm ;zI兲 =
␾p共x,y,zI兲 =
r,s
by the use of Eq. (6) and a first-order approximation with
respect to ⌬z for the exponential term representing the
perturbed electric field.
共8兲
where the total complex phase ␾共x , y , zI兲 is the sum of the
incident complex phase ␾0共x , y , zI兲 and the perturbed complex phase ␾p共x , y , zI兲. The incident electric field
U0共x , y , zI兲 = exp关␾0共x , y , zI兲兴 provides the incident phase
function, and the perturbed complex phase is calculated
by
where z0 is the in-focus plane. Thus, the first Born approximation model calculates the total electric field at the
image plane by substituting Eqs. (6) and (7) into Eq. (1).
2. First Rytov Approximation
The first Rytov approximation is derived under the assumption that the phase change of the perturbed or scattered field over one wavelength is small [20]. The validity
conditions for the first Rytov approximation are slightly
different and somewhat less restrictive than the first
Born approximation conditions.
The total electric field at the image plane can be represented as a complex phase function,
1271
冣
,
共11兲
sumption that each object slice contributes to the total object phase, we can write an expression for the total phase
object at the image plane,
m=N
␾p⬘ 共x,y,zI兲 =
兺
␾p⬘ 共x,y,zm ;zI兲,
共14兲
m=−N
and equivalently an expression for the total object at the
image plane,
m=N
g共x,y,zI兲 =
兿
m=−N
冕冕
exp关jkn␦共x̃,ỹ,zm兲⌬z兴
r,s
⫻h共x − x̃,y − ỹ,zI − zm兲dx̃dỹ.
共15兲
This approach is similar to a projection approach, in
which the total phase is calculated as a ray-casting projection along the optical axis [37,38]. However, the POC
model includes an interaction along the lateral axes and
diffraction effects in the optical system through the convolution between each object slice and a 2D slice of the
PSF.
The total electric field at the image plane U共x , y , zI兲 is
then calculated as the product of the object function
g共x , y , zI兲 and the unperturbed incident field U0共x , y , zI兲 at
the image plane,
U共x,y,zI兲 = U0共x,y,zI兲g共x,y,zI兲,
共16兲
where U0共x , y , zI兲 is the same unperturbed incident field
defined in Eq. (7).
1272
J. Opt. Soc. Am. A / Vol. 26, No. 5 / May 2009
Sierra et al.
3. EXPERIMENTS
To test the POC model we compare it to both the Born and
Rytov methods. First, we provide a numerical evaluation
of each image model, identifying the strengths and weaknesses for each, using simple objects with varying thicknesses. Second, we simulate images of homogeneous objects using the three models and compare the resulting
images to experimental images. Third, we simulate more
complex heterogeneous objects and show that the
strengths of the POC model make it suitable to simulate
images of objects that are similar to experimental images
of biological samples. The experimental phase images utilized in the comparisons were generated using an optical
quadrature microscopy (OQM) imaging modality that
noninvasively provides the amplitude and phase of an optically transparent sample [5,39].
The synthetic phase images were created using the
PSF model with the Born, Rytov, and POC models as described in Section 2. The PSF was computed using an illumination wavelength of ␭ = 0.633 ␮m and a 10⫻ objective lens with a numerical aperture of 0.500. Each set of
resultant images was compared to a simulated image using a phase projection model [37,38]. The phase projection
model neglects diffraction and provides the optical path
difference (OPD):
OPD共x,y兲 =
冕
d共x,y兲
n␦共x,y,z兲dz.
共17兲
0
The total OPD is the integral of the index of refraction
difference between the object and the medium n␦共x , y , z兲
over a distance d共x , y兲, which is the total physical thickness of the object along the optical axis. This projection
will be used as the basis for comparison with the synthesized images.
OQM and simulated images that have phase values
greater than 2␲ were unwrapped using a 2D Lp-norm algorithm [40]. The corresponding OPD images were calculated by dividing the unwrapped phase images by the
wave number k. Note that no perturbation in the index of
refraction along the optical axis resulted in a zero OPD
value.
A. Numerical Evaluation of the Models Using a
Rectangular Solid Object
We simulated two rectangular solid objects to model glass
blocks of differing thickness both with an index of refraction of 1.550 and a width of 41 ␮m, immersed in oil with
an index of refraction of n0 = 1.515. Thus the difference in
index of refraction was n␦ = 0.035. The objects have thicknesses of 2 and 35 ␮m, respectively. This experiment tests
the accuracy of each model at representing both thin and
thick objects. Figure 3(a) shows a phase slice through either object geometry at the middle of the glass block. Figures 3(b) and 3(c) show the profiles of the simulated OPD
from the unwrapped simulated phase images at the center of the square object using the projection, POC, Rytov,
and Born models. As Fig. 3(b) shows, all models are capable of representing with similar fidelity an OPD that
matches the projection model for the case of thin objects.
However, when the object thickness is larger, as in Fig.
3(c), the OPD representation obtained by the POC model
Fig. 3. OPD profile comparison of a synthetic uniform square
object with n␦ = 0.035 taken at the middle of the object. (a) A
transverse slice through either object at the center of the glass
block, (b) comparison of simulated OPD as a function of position
along the x axis at y = 0 ␮m for the object with a thickness of
2 ␮m, and (c) similar comparison of simulated OPD for an object
with a thickness of 35 ␮m.
is the only one that matches the projection model with essentially the same accuracy as before. The Rytov model
shows some degradation in its OPD results and the Born
shows much worse degradation.
Figure 4 shows calculations of the OPD values at the
center of the square in the xy plane as a function of the
thickness. At each thickness the average of the five OPD
values closest to the center of the object was used to provide a better approximation of the central value. It is
clearly seen that the POC model obtained the most accurate OPD in cases where the object thickness was large.
The Rytov model worked relatively well over this range of
object thickness variation, while the limitations of the
first Born approximation were again confirmed when the
Sierra et al.
Vol. 26, No. 5 / May 2009 / J. Opt. Soc. Am. A
1273
object was optically thick. The POC, Rytov, and Born models had an rms error of 0.001, 0.004, and 0.140, respectively, when compared to the projection model.
Fig. 4. OPD comparison from images of uniform square objects
as a function of varying thicknesses. The plot shows for each
thickness the OPD averaged over the five OPD values closest to
the center of the object along a profile taken at the middle of the
object.
B. Comparison of Simulated and Experimental Phase
Images from a Uniform Sphere
The second simulated object was a uniform sphere with a
radius of 37 ␮m and an index of refraction of 1.492 submerged in a uniform medium with an index of refraction
of n0 = 1.515. This provides a difference in index of refraction of n␦ = −0.023. We note that n␦ ⬍ 0 induces negative
OPD, as the object is immersed in a medium with a
higher index of refraction than the background. The optical properties of the simulation were chosen to match
those of an experimental poly(methyl methacrylate)
(PMMA) bead in oil. A cartoon slice through the object geometry at the middle of the sphere is shown in Fig. 5(a).
Figures 5(b)–5(e) show the OPD images from the simulated unwrapped phase images using the projection, POC,
Rytov, and Born models, respectively. Figure 5(f) shows
Fig. 5. Simulated and measured OPD images of a PMMA bead in oil. All images are shown with the same scale and contrast. (a) Cartoon of the cross section of the real part of the simulated PMMA bead in oil, (b) projection model, (c) POC, (d) Rytov, (e) Born, (f) OQM
measured image of a real bead matching the model, and (g) plot of the profile of simulated and measured OPD images.
1274
J. Opt. Soc. Am. A / Vol. 26, No. 5 / May 2009
the OPD image from an experimentally obtained OQM
phase image of a real PMMA bead that matches the computational model.
We observe that for Born and Rytov models the peak
OPD values are above ⫺1.00 and −1.47 ␮m, respectively,
while the POC and projection models report a peak OPD
value of −1.67 ␮m and the measured image has a maximum phase value of −1.66 ␮m. These results illustrate
that the relative behavior of the models is similar for
simulating phase images of a thick PMMA bead and for
simulating the thick square object.
C. Comparison of Synthetic and Measured Phase Images
from a Nonuniform Object
A nonuniform object model was created based on previously obtained observations of experimental phase images from one-cell mouse embryos. The object model consisted of a large sphere with a radius of 35 ␮m containing
Sierra et al.
an off-center smaller sphere with a radius of 12.5 ␮m representing the nucleus [see Fig. 6(a)]. The center of the
smaller sphere was placed 17.5 ␮m to the right of the center of the larger one. The small and large spheres had indices of refraction of 1.37 and 1.35, respectively, again
simulating the nucleus and the cytoplasm of the cell [41].
Mitochondria inside the cytoplasm were simulated as
small rectangular solid particles, of the size of 1.5 ␮m
⫻ 0.5 ␮m ⫻ 0.5 ␮m with an index of refraction of 1.43,
placed randomly inside the larger sphere but outside the
smaller one at different orientation angles chosen randomly to be any of the following: 兵−␲ / 4 , 0 , ␲ / 4其 for all
共x , y , z兲 coordinates.
A 9 ␮m wide shell was placed surrounding the larger
sphere to simulate the zona pellucida of the embryo, the
region surrounding the cytoplasm. The shell had an index
of refraction of 1.34; a common value found in literature
[41]. The entire object was simulated as being immersed
Fig. 6. Measured and simulated OPD images of a one-cell mouse embryo. All images are shown with the same scale and contrast. (a)
Slice of the real part of the synthetic object. Small bright particles represent the mitochondria while the small and large spheres represent the nucleus and cytoplasm, respectively, and the outer shell surrounding the large sphere simulates the zona pellucida. (b) Projection, (c) POC, (d) Rytov, (e) Born, (f) experimental measured OQM image of a typical embryo, (g) profiles taken at the middle of the
simulated OPD images, and (h) OPD profile taken at the middle of the OQM image.
Sierra et al.
in a medium with index of refraction of 1.33. Figure 6(a)
shows a slice through the object geometry at a depth
equal to 35 ␮m, corresponding to the center of the larger
sphere.
Figures 6(b)–6(e) show OPD images of simulated unwrapped phase images using projection, POC, Rytov, and
Born models, respectively, of the nonuniform object. The
OPD of a measured unwrapped phase image from a onecell mouse embryo—again using an OQM—is shown in
Fig. 6(f). The diameter of a mouse embryo is approximately 90 ␮m, including the zona pellucida, with a corresponding OPD of 2.52 ␮m. We observe that simulated images using the Born and Rytov models have maximum
OPD values of 0.08 and 1.50 ␮m while the projection and
POC models have maximum OPD value of 2.54 and
2.52 ␮m, respectively. We plot the profile of the OPD images at the center of the object to better demonstrate our
results in Figs. 6(g) and 6(h). Figure 6(g) illustrates the
poor accuracy of the Born and Rytov models when comparing them to the projection model and shows that the
POC model gives the best representation of the OPD. The
profile of the measured image is shown in Fig. 6(h) to illustrate the shape and maximum value of the OPD of the
experimental one-cell embryo image.
4. CONCLUSIONS
In this paper we have simulated phase microscope images
with forward models based on the first Born and Rytov
approximations and compared them to the simulated data
using a proposed POC model. The implementation complexity of the three models is comparable. Simulated OPD
images from homogeneous and heterogeneous objects
were produced in order to compare the ability of each
model to generate correct phase images of thick objects.
The results when calculating the OPD of the simulated
images show that the POC model is capable of representing phase images of thick objects without suffering degradation in accuracy for thick objects and large index of refraction variations, which limit the accuracy that can be
obtained from the Born and Rytov models. The results
also show that information about the object shape is detectable in simulated images with Rytov and POC models.
We have illustrated the ability of the POC model to represent the phase image of an inhomogeneous object with
reasonable fidelity under real conditions where both the
Born and Rytov models failed.
The accuracy of the POC model for predicting phase images depends on the resolution of the discretization routine. Since each object slice is considered to be uniform in
z when calculating the image, rapid changes in the index
of refraction along the optical axis might produce a highly
inaccurate image representation if the z-axis discretization is not fine enough to capture these variations. Another limitation of the POC model is that the backscattered field is not considered; only the contributions that
travel in the forward direction through each slice are
taken into account. As future work, we will be considering
the application of the POC model for simulating other
phase microscope techniques such as DIC microscopy, as
well as the use of the POC model to generate full 3D images.
Vol. 26, No. 5 / May 2009 / J. Opt. Soc. Am. A
1275
Another area for future work is to compare POC and
BPM. We have generated synthetic images using BPM for
the same objects described in this paper and observed interesting differences from POC results when there is a
large variation in geometry and index of refraction of the
object along the optical axis. In particular, we observed a
blur effect in the BPM images, localized at the edges of
the objects. These results suggest that there are some differences between the POC and BPM methods in their
ability to accurately represent sharp edges of optically
thick objects, as well as their relative sensitivity to arbitrary modeling decisions such as the edge of the computational object volume. However, to better contrast these
differences and similarities to the POC model results, a
more rigorous comparison needs to be done. Due to space
limitations, we reserve this comparison for another report.
ACKNOWLEDGMENTS
This work was supported in part by the Bernard M. Gordon Center for Subsurface Sensing and Imaging Systems
(Gordon-CenSSIS) under the Engineering Research Centers Program of the National Science Foundation (NSF)
(award EEC-9986821). The authors thank Bill Warger of
Northeastern University for helpful discussions and assistance in capturing the images. The authors also thank
an anonymous reviewer for constructive comments and
suggestions.
REFERENCES
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
W. Lang, “Nomarski differential interference contrast
microscopy. II. formation of the interference image,” Zeiss
Inform. 17, 12–16 (1969).
H. Ishiwata, M. Itoh, and T. Yatagai, “A new method of
three-dimensional
measurement
by
differential
interference contrast microscope,” Opt. Commun. 260,
117–126 (2006).
P. Marquet, B. Rappaz, P. J. Magistretti, E. Cuche, Y.
Emery, T. Colomb, and C. Depeursinge, “Digital
holographic microscopy: a noninvasive contrast imaging
technique allowing quantitative visualization of living cells
with subwavelength axial accuracy,” Opt. Lett. 30, 468–470
(2005).
N. Lue, W. Choi, G. Popescu, T. Ikeda, R. R. Dasari, K.
Badizadegan, and M. S. Feld, “Quantitative phase imaging
of live cells using fast Fourier phase microscopy,” Appl.
Opt. 46, 1836–1842 (2007).
D. O. Hogenboom, C. A. DiMarzio, T. J. Gaudette, A. J.
Devaney, and S. C. Lindberg, “Three-dimensional images
generated by quadrature interferometry,” Opt. Lett. 23,
783–785 (1998).
E. D. Barone-Nugent, A. Barty, and K. A. Nugent,
“Quantitative phase-amplitude microscopy I: optical
microscopy,” J. Microsc. 206, 194–203 (2002).
E. Cuche, F. Bevilacqua, and C. Depeursinge, “Digital
holography for quantitative phase-contrast imaging,” Opt.
Lett. 24, 291–293 (1999).
S. R. P. Pavani, A. Libertun, S. King, and C. Cogswell,
“Quantitative structured-illumination phase microscopy,”
Appl. Opt. 47, 15–24 (2008).
D. B. Murphy, Fundamentals of Light Microscopy and
Electronic Imaging (Wiley-Liss, 2001).
W. Choi, C. Fang-Yen, K. Badizadegan, S. Oh, N. Lue, R. R.
Dasari, and M. S. Feld, “Tomographic phase microscopy,”
Nat. Methods 4, 717–719 (2007).
C. Fang-Yen, S. Oh, Y. Park, W. Choi, S. Song, H. S. Seung,
1276
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
J. Opt. Soc. Am. A / Vol. 26, No. 5 / May 2009
R. R. Dasari, and M. S. Feld, “Imaging voltage-dependent
cell motions with heterodyne Mach–Zehnder phase
microscopy,” Opt. Lett. 32, 1572–1574 (2007).
H. Gundlach, “Phase contrast and differential interference
contrast instrumentation and application in cell,
developmental, and marine biology,” Opt. Eng. 32,
3223–3228 (1993).
C. J. R. Sheppard and M. Gu, “Modeling of 3-D brightfield
microscope systems,” Proc. SPIE 2302, 352–358 (1994).
C. Preza, D. L. Snyder, and J. A. Conchello, “Theoretical
development and experimental evaluation of imaging
models for differential-interference contrast microscopy,” J.
Opt. Soc. Am. A Opt. Image Sci. Vis. 16, 2185–2199 (1999).
C. J. Bellair, C. L. Curl, B. E. Allman, P. J. Harris, A.
Roberts, L. M. D. Delbridge, and K. A. Nugent,
“Quantitative phase-amplitude microscopy IV: imaging
thick specimens,” J. Microsc. 214, 62–70 (2004).
N. Streibl, “Three-dimensional imaging by a microscope,” J.
Opt. Soc. Am. A 2, 121–127 (1985).
I. Nemoto, “Three-dimensional imaging in microscopy as an
extension of the theory of two-dimensional imaging,” J.
Opt. Soc. Am. A 5, 1848–1851 (1988).
F. C. Lin and M. A. Fiddy, “The Born–Rytov controversy. I.
comparing analytical and approximate expressions for the
one-dimensional deterministic case,” J. Opt. Soc. Am. A 9,
1102–1110 (1992).
B. Chen and J. J. Stamnes, “Validity of diffraction
tomography based on the first Born and the first Rytov
approximations,” Appl. Opt. 37, 783–785 (1998).
A. C. Kak and M. Slaney, Principles of Computerized
Tomographic Imaging (Society for Industrial and Applied
Mathematics, 2001).
C. J. Cogswell and C. J. R. Sheppard, “Confocal differential
interference contrast (DIC) microscopy: including a
theoretical analysis of conventional and confocal DIC
imaging,” J. Microsc. 165, 81–101 (1992).
F. Kagawala and T. Kanade, “Computational model of
image formation process in DIC microscopy,” Proc. SPIE
3261, 193–204 (1998).
J. L. Hollmann, A. K. Dunn, and C. A. DiMarzio,
“Computational microscopy in embryo imaging,” Opt. Lett.
29, 2267–2269 (2004).
D. L. Marks, “A family of approximations spanning the
Born and Rytov scattering series,” Opt. Express 14,
8837–8848 (2006).
G. Beylkin and M. L. Oristaglio, “Distorted-wave Born and
distorted-wave Rytov approximations,” Opt. Commun. 53,
213–216 (1985).
W. Choi, C. Fang-Yen, K. Badizadegan, R. R. Dasari, and
M. S. Feld, “Extended depth of focus in tomographic phase
Sierra et al.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
microscopy using a propagation algorithm,” Opt. Lett. 33,
171–173 (2008).
G. A. Tsihrintzis and A. J. Devaney, “Higher-order
(nonlinear)
diffraction
tomography:
reconstruction
algorithms and computer simulation,” IEEE Trans. Image
Process. 9, 1560–1572 (2000).
N. Dey, A. Boucher, and M. Thonnat, “Image formation
model a 3 translucent object observed in light microscopy,”
in Proceedings of 2002 Conference on Image Processing
(IEEE, 2002), Vol. 2, pp. 469–472
F. Truchetet and O. Laligant, “Optical tomography from
focus,” Opt. Express 15, 7381–7392 (2007).
J. Van Roey, J. van der Donk, and P. E. Lagasse, “Beampropagation method: analysis and assessment,” J. Opt. Soc.
Am. 71, 803–810 (1981).
D. Yevick and D. J. Thomson, “Complex Padé approximants
for wide-angle acoustic propagators,” J. Acoust. Soc. Am.
108, 2784–2790 (2000).
K. Q. Le and P. Bienstman, “Wide-angle beam propagation
method without using slowly varying envelope
approximation,” J. Opt. Soc. Am. B 26, 353–356 (2009).
S. F. Gibson and F. Lanni, “Diffraction by a circular
aperture as a model for three-dimensional optical
microscopy,” J. Opt. Soc. Am. A 6, 1357–1367 (1989).
M. Born and E. Wolf, Principles of Optics (Cambridge U.
Press, 2001).
J. W. Goodman, Introduction to Fourier Optics (McGrawHill, 1999).
H. Sierra, C. A. DiMarzio, and D. H. Brooks, “Modeling
images of phase information for three-dimensional objects,”
Proc. SPIE 6861, 68610A.1–68610A.9 (2008).
F. Charrière, N. Pavillon, T. Colomb, C. Depeursinge, T. J.
Heger, E. A. D. Mitchell, P. Marquet, and B. Rappaz,
“Living specimen tomography by digital holographic
microscopy: morphometry of testate amoeba,” Opt. Express
14, 7005–7013 (2006).
F. A. Jenkins and H. White, Fundamentals of Optics
(McGraw-Hill, 1976).
W. C. Warger II, G. S. Laevsky, D. J. Townsend, M.
Rajadhyaksha, and C. A. DiMarzio, “Multimodal optical
microscope for detecting viability of mouse embryos in
vitro,” J. Biomed. Opt. 12, 044006 (2007).
D. Ghiglia and M. Pritt, Two-Dimensional Phase
Unwrapping: Theory, Algorithms, and Software (Wiley,
1998).
R. Drezek, A. Dunn, and R. Richards-Kortum, “Light
scattering from cells: finite-difference time-domain
simulations and goniometric measurements,” Appl. Opt.
38, 3651–3661 (1999).