* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 3
Survey
Document related concepts
Transcript
May 18, 2011 Section 9.3 Probability Probability of an Event (equally likely outcomes) If E is an event in a finite, nonempty sample space S of equally likely outcomes, then the probability of the event E is P(E) = sample space: the set of all possible outcomes of an experiment What is the sample space when a red and green die are rolled simultaneously? (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) What is the probability that the sum of the dice totals 9? What is the probability that the sum of the dice totals less than 9? 1 May 18, 2011 Probability Function A probability function is a function P that assigns to each outcome in a sample space a unique real number, subject to the following conditions: 1. 0 ≤ P(O) ≤ 1 for every outcome O; 2. the sum of the probabilities of all outcomes in S is 1; 3. P(∅) = 0. Multiplication Principle of Probability Suppose an event A has probability p1 and an event B has probability p2 under the assumption that A occurs. Then the probability that A and B occur is p1⋅p2. 12. P(not red) = 1 − 0.2 = 0.8 18. P(first brown and second is yellow) 0.3 ⋅ 0.2 = 0.06 2 May 18, 2011 23. P(4 aces) = Ten dimes dated 2000 through 2009 are tossed. Find the probability of each event. P(the 2005 dime is a tails) = 1/2 P(heads on exactly 4 dimes) P(tails on exactly 4 dimes) P(tails on exactly 6 dimes) P(heads on at least 2 dimes) 3 May 18, 2011 Find the probability that no two people in a group of n people share the same birthday. Let n be 25. Consider that no two people share the same birthday. notice that and 4 May 18, 2011 A certain test to detect the presence of the AIDS antibody will test positive 99.7% of the time if a person has the antibody and give a false negative 0.3% of the time. It will give a false positive 1.5% of the time. As of 2003, P(HIV/AIDS) for the general population in the U.S. was 0.006. How effective is this test. P(true +) = .997 P(have) = .006 P(false −) = .003 P(false +) = .015 P(not) = .994 P(true −) = .985 5 May 18, 2011 Binomial Probability Where p is the probability of a success, and q is the probability of a failure (which is complementary to p, that is q = 1 − p). Suppose it is known that 1 out of every 350 light bulbs produced by a certain machine is defective. Find the probability that 2 bulbs in a sample of 5 will be defective. 6 May 18, 2011 7 May 18, 2011 8






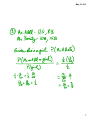


![[Type Book Title here] Name: Section: Chapter 4 Test Form F 1](http://s1.studyres.com/store/data/010766429_1-cbfeb3d24d58c60cae31ac47865c83f2-150x150.png)









