Download Midterm Exam #3 - Indiana HEP, Astrophysics and Theory

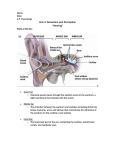
Name:
ID #:
Midterm Exam #3
P105 - Basic Physics of Sound - Fall 2001
Closed book. You are allowed a calculator.
Friday 16 Nov. 2001, 10:10 – 11:00 a.m.
Circle one and only one answer as the “best” answer or fill in/sketch the best answer.
Where applicable, show your work (on back if necessary) – partial credit is possible.
Each question is worth 4 points unless otherwise indicated.
1. During summer vacation, you are swimming underwater and your ear canal of length
L = 3.0 cm is filled with water. It can be treated as a column of fluid open at one end
and closed at the other (eardrum). Given that the velocity of sound in water is
water
v sound = 1435 m/s , at what frequency will you ear be most sensitive due to resonance in
your ear canal? (this is one of the reasons that what you hear underwater seems very different).
A) 480 Hz;
B) 2,620 Hz;
C) 3,990 Hz;
D) 11,960 Hz;
E) 15,650 Hz.
nv
1435 m/s
Tube closed at one end, open at other: f n = ------ , f 1 = ------------------------------ = 11960 Hz ,
4L
( 4 ) ( 0.03 m )
(D)
2. A tiny mouse has ears that are approximately d = 2.0 cm = 0.02 m apart. Assume
that diffraction is important only for wavelengths equal to or greater than this distance.
For which frequencies will the mouse have difficulty judging the direction of a source of
air
sound by using the difference in intensities detected in each ear? ( v sound = 343 m/s )
A) f > 17150 Hz ;
B) f ≤ 17150 Hz ;
C) f > 8880 Hz ;
D) f ≤ 8880 Hz ;
E) f > 2020 Hz ;
F) f ≤ 2020 Hz
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
1
Name:
ID #:
Our poor little mouse will have difficulty judging the direction of a source of sound via
intensity differences in its ears if diffraction is important such that the sound waves bend
around its head allowing almost equal intensity at each ear. Diffraction is not significantly important for wavelengths λ < d , where d is the distance between the ears of the
343 m/s
v
mouse, i.e., if λ = d = 0.02 m , f = --- = ------------------- = 17150 Hz . For frequencies lower
0.02 m
λ
than this, wavelength is longer, diffraction is important, and the mouse will have difficulties for frequencies f ≤ 17150 Hz , i.e., (B(.
3. (8 pts) Two tones of frequency 600 Hz and 900 Hz and of equal amplitudes are played
together.
(a) Which tone will excite the Basilar membrane closer to the oval window?
Check out Figure 6-3 in your text. Higher frequencies will tend to excite the Basilar membrane closer to the oval window while lower frequencies will excite the membrane further down the cochlea/membrance. Therefore the 900 Hz tone will be the one that
excites the membrane closer to the oval window.
(b) What property of the Basilar membrane explains this, and what is the theory called
describing the response of the membrane to different frequencies at different distances
from the oval window?
Closer to the oval window, the membrane is thin and stretched taut so it will tend to resonate at higher frequencies. Further down the cochlea and membrane, it is thicker (more
mass per unit area, more inertia, difficult to accelerate quickly) and stretched looser, and
its natural frequency at that point would be at a lower frequency. The theory describing
this response is the Place Theory of Hearing.
(c) Which of the two tones is expected to mask the other tone more effectively?
Lower frequencies more effectively mask higher frequencies; therefore, the 600 Hz tone
will mask the 900 Hz tone more effectively than vice versa.
(d) Give two roles of the middle ear in the hearing process.
(i) The force at the ear drum from acoustic pressure wave is amplified while being
transmitted by the middle ear to the oval window due to the lever action of the anvil,
hammer, and stirrup (ossicle bones) and the relative areas between the ear drum and
oval window.
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
2
Name:
ID #:
(ii) During sudden loud sounds, the stirrup retracts from the oval window in the acoustic reflex that provides protection of the inner ear.
(iii) Can simply say also that the middle ear conducts pressure waves from the ear
drum to the oval window (inner ear) as well as affording a mechanism to equalize the
pressure on both sides of the ear drum via the Eustachion tube.
4. (8 pts) Use the attached copy of Figure 6-4 from Berg to answer the questions below:
(a) What is the loudness level in phons of a tone with frequency f = 100 Hz with a
sound intensity level (SIL) of 40 dB?
~0
phons.
Draw a vertical line at f = 100 Hz and a horizontal line at SIL = 40 dB. You should find
them intersecting at the 0 phon equal loudness curve.
(b) What is the sound intensity level (SIL) of a second tone at a frequency of
f = 1000 Hz that is perceived as having the same loudness as the tone above?
SIL =
~0
dB
By definition, if the sound above lies on the 0-phon line of equal loudness, normalization
is such that 0 phons at 1000 Hz is exactly a sound intensity level SIL = 0 dB.
(c) In the figure, explain the dip at 4000 Hz.
This dip is due to the first resonance in the ear canal that behaves as a tube open at one
end and closed at the other. Due to this resonance, the ear is most sensitive (i.e., threshold of hearing) is at the lowest absolute intensity level in dB at this frequency of approximately 4000 Hz.
5. (8 pts) Fill in the missing parts of the table below:
Table 1:
Sound Quality
Pitch/frequency
Loudness/volume/
intensity
Nerve signal in inner ears
Where along the basilar membrane nerve cells are
firing
How often the nerve cells fire.
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
3
Name:
ID #:
Table 1:
Sound Quality
Timbre
Direction
Nerve signal in inner ears
Which groups of nerve cells are firing simultaneously (i.e., amplitude of frequency components)
Either nerve cells in one ear are firing more often
than in the other testing for intensity difference,
and/or the timing of nerve signals between ears
will be slightly different.
6. (6 pts) Critical Bands: For each combination below of two tones with frequencies
f A, f B presented simultaneously, what is heard? (circle True or False, fill in blanks, show
your work/justification).
fA + fB
1900 + 2100 Hz
(a) f A = 1900 Hz, f B = 2100 Hz f 0 = ------------------ = --------------------------------------- = 2000 Hz ,
2
2
∆f = 0.12 × f 0 = 0.12 × 2000 Hz = 240 Hz . f A – f B = 200 Hz < ∆f = 240 Hz , therefore both frequencies in the same critical band,
(i) Single fused frequency?
T
F
If true, frequency of fused tone =
2000 Hz
F
(ii) Two separate frequencies? T
Only hear beats if f A – f B < 15 Hz ,
(iii) Beats heard?
T
(b) f A = 240 Hz, f B = 360 Hz
f 0 < 500 Hz, ∆f = 90 Hz f A – f B
are not in the same critical band.
(i) Single fused frequency?
F
fA + fB
240 + 360 Hz
- = --------------------------------- = 300 Hz ,
f 0 = -----------------2
2
= 120 Hz > ∆f = 90 Hz , therefore both frequencies
T
(ii) Two separate frequencies? T
F
If true, frequency of fused tone =
Hz
F
Only hear beats if f A – f B < 15 Hz ,
(iii) Beats heard?
T
F
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
4
Name:
ID #:
fA + fB
3000 + 3010 Hz
- = --------------------------------------- = 3005 Hz
(c) f A = 3000 Hz, f B = 3010 Hz f 0 = -----------------2
2
∆f = 0.12 × f 0 = 0.12 × 3005 Hz = 360 Hz f A – f B = 10 Hz < ∆f = 360 Hz . Therefore in the same critical band; also frequency difference is small enough to hear beats.
(i) Single fused frequency?
T
F
(ii) Two separate frequencies? T
F
T
F
(iii) Beats heard?
If true, frequency of fused tone =
Hz
7. (6 pts) What frequency is 3 octaves above a frequency of f = 3000 Hz ?.
Each octave is a doubling of frequency so we have to have three doublings:
3000 Hz × 2 × 2 × 2 = 24000 Hz , i.e, (E)
A) 6,000 Hz;
B) 18,000 Hz;
C) 15,000 Hz;
D) 30,000 Hz;
E) 24,000 Hz.
The frequency response of a typical adult is about 30 – 16,000 Hz, so this would be
beyond the range of hearing:
Is this beyond the normal frequency response range of a typical adult?
Yes No
8. Bernoulli’s principle is responsible for:
A) pushing the vocal flaps (cords) open with increased air velocity;
B) causing the vocal flaps (cords) to close when air velocity increases between
them;
C) changing the effective length of the vocal tract;
D) transforming vibrations in the Basilar membrane to nerve signals.
Normal pressure increase opens the flaps with increased air velocity, but it this
increased air velocity with subsequent pressure drop due to Bernoulli’s principle
that causes them to close, i.e., (B)
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
5
Name:
ID #:
9. Pete Townshend is experiencing loss of hearing (after many years of touring...) When
a tuning fork is set vibrating and its handle held against the bone of his skull, he can easily hear a whole range of frequencies. He is most likely suffering from partial:
A) conduction deafness;
B) nerve deafness;
C) degeneration of the cochlea;
D) separation of the Organ of Corti from the Basilar membrane.
If Pete can hear this sound through his skull, then the inner ear and all the
machinery converting vibrations into electrical and nerve signals is intact, i.e, not
nerve deafness or any of the other choices. He has problems in the conduction
path to the inner ear, i.e. conduction deafness, (A).
10. Three tones of frequencies of 200 Hz, 300 Hz, and 600 Hz are played simultaneously.
Will these sound consonant or dissonant, and why?
Write out the harmonic series for each tone:
200 Hz: 200 400 600 800 1000 1200 1400 1600 1800 2000 ... Hz
300 Hz: 300 600 900 1200 1500 1800 2100 ... Hz
600 Hz: 600 1200 1800 ... Hz
Note how they all share exactly harmonics at 600, 1200, and 1800 Hz, they will therefore
sound consonant.
More on next page!
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
6
Name:
ID #:
10. (10 pts) The three frequency spectra recorded at the output of the vocal tract (i.e., the
mouth) shown below depict three different sounds that are vowels voiced in normal conversation:
Fill in the blanks:
(a) Which spectra are of the same vowel sound but at different pitch?
The same vowel sounds will show the same relative pattern of harmonic amplitudes, i.e.,
look for the same envelope of frequency amplitudes:
(i) and (iii)
(b) Which spectra are of different vowel sounds, but at the same pitch?
Now you don’t care about he envelope or pattern of harmonics, just that they have harmonic series with the same fundamental. (i) and (ii) both have fundamental frequencies
of 250 Hz.
(i) and (ii)
(c) What is the pitch of the sound described by spectrum (iii)?
Look for the fundamental frequency, in this case, the frequency of the lowest frequency
“spike”
125
Hz.
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
7
Name:
ID #:
(d) What are the formant frequencies in spectrum (iii)? Read them off
F 1 = 750 Hz , F 2 = 1750 Hz
(e) Spectrum (iii) is a vowel most likely voiced by a male or female?
Check out the answer for (c). The pitch of the input to the vocal tract is low, i.e., 125 Hz.
This is indicative of a male.
male
.
(f) Sketch in (iv) the filter function responsible for the spectrum shown in (ii).
(assume a flat input frequency spectrum from the vocal cords, i.e., the amplitudes of all
the harmonic frequencies as being equal)
Follows the envelope of (ii) directly above it, i.e., no spikes, just smooth formant peaks
where the frequencies in (ii) are being enhanced.
Formulae Sheet
Conversion Factors: 1 m = 3.281 ft ; 1 in = 2.54 cm ; 1 mile = 5280 ft ; 1 kg = 2.20 lbs ;
3
1 hour = 3, 600 s ; 1 liter = 1, 000 cm ; 1 horsepower = 746 Watts ; 2π radians = 360° ;
2
kg ⋅ m
kg ⋅ m
cycle
- ; 1 J = 1 N ⋅ m = ---------------- ; 1 Hz = 1 -------------1 N = 1 -------------2
2
s
s
s
Standard Prefixes: mega
M
10
kilo
k
10
centi
c
10
milli
m
10
Midterm Exam #3, P105, Basic Physics of Sound
6
3
–2
–3
16 Nov. 2001
8
Name:
ID #:
micro
µ
10
nano
n
10
–6
–9
x f – xi
∆x
∆x
Velocity, speed v = ------ ; Average speed over time interval ∆t : v = ------ = --------------t f – ti
∆t
∆t
v f – vi
∆v
- ; Distance travelled d = vt
Acceleration: a = ------ = -------------∆t
t f – ti
Newton’s Second Law: F = ma ; ; Force due to a spring: F = – kx
F
1 2
Pressure: P = ------⊥- ; Kinetic Energy: KE = --- mv
2
A
W
E
Power: P = ----- = --t
t
1 k
1
Frequency, period: f = --- ; Frequency mass/spring system: f = ------ ---2π m
T
2πt
Motion of Simple Harmonic Oscillator: x = x max cos  --------
 T 
Speed of sound at room temperature ( T = 21°C ), v sound = 343 m/s .
Change in frequency due to Doppler Effect:
v sound ± v o
(i) Observer moving, source stationary, f 0 = f s  -------------------------- ; (+ approaching, – receding)
 v sound 
v sound 
- (– approaching, + receding)
(ii) Source moving, observer stationary: f 0 = f s  ----------------------- v sound −
+ v s
Relation between wave speed, wavelength, and frequency: v = fλ
Two tones, f A and f B beat frequency f beat = f B – f A is the frequency of the resultant
( f A + f B)
- .
amplitude modulation at a sum frequency of f sum = ----------------------2
Importance of diffraction: If encountering an opening of approximate diameter d, or an
obstacle of typical size d, diffraction is
(i) important for λ ≥ d ; and (ii) much less important when λ « d .
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
9
Name:
ID #:
Angle between perpendicular to line joining sound sources distance d apart and m-th
mλ
region of constructive interference: sin θ = ------- .
d
Harmonic series for standing waves on a string of length L and mass per unit length µ :
n T
nv
f n = n f 1 = ------ = ------ --- with n = 1, 2, 3, … .
2L µ
2L
Harmonic series for standing waves in a pipe of length L , open at both ends:
nv sound
f n = n f 1 = ----------------- , with n = 1, 2, 3, … .
2L
Harmonic series for standing waves in a pipe of length L , open at one end and closed at
the other:
nv sound
- , with n = 1, 3, 5, … .
f n = n f 1 = ----------------4L
Sound Level:
I
– 12
2
Sound intensity level, SIL = 10 log  ---- with I 0 = 10
W/m the reference intensity;
 I 0
p
–5
2
Sound pressure level, SPL = 20 log  ----- with p o = 2 ×10 N/m the reference pressure.
 p 0
Table 2: Relative amplitudes of harmonics present in the standard waves
Wave
Harmonic Amplitudes
n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
Sine
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
Triangle
1
1
1
1
1, 0, ---, 0, ------, 0, ------, 0, ------, 0, …
9
25
49
81
Square
1
1
1
1
1, 0, ---, 0, ---, 0, ---, 0, ---, 0, …
3
5
7
9
Sawtooth (ramp)
Midterm Exam #3, P105, Basic Physics of Sound
1 1 1 1 1 1 1 1 1
1, ---, ---, ---, ---, ---, ---, ---, ---, ------, …
2 3 4 5 6 7 8 9 10
16 Nov. 2001
10
Name:
ID #:
Table 2: Relative amplitudes of harmonics present in the standard waves
Wave
Harmonic Amplitudes
n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
Pulse train
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
Critical bands: Two tones of frequency f A and f B are presented simultaneously
( f A + f B)
f 0 = ----------------------2
To find critical bandwidth, ∆f , there are two conditions:
(i) If f 0 < 500 Hz , then ∆ f ≈ 90 Hz , otherwise,
First find the “central frequency”,
(ii) If f 0 ≥ 500 Hz , then ∆f = 0.12 × f 0 .
Now check:
(a) if f A – f B < ∆f , then hear single fused frequency of value f 0 ; else if
(b) if f A – f B > ∆f , then hear two separate tones at frequency of f A and f B .
Midterm Exam #3, P105, Basic Physics of Sound
16 Nov. 2001
11