Download File - Jason Morton ePortfolio

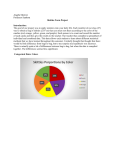
Math 1040 Skittles Project -­‐‑ Part I and Worksheet Jason Morton Part I. For your own single 2.17-­‐‑ounce bag of Skittles, record the numbers in the table below. Number of red candies Number of Number of Number of Number of orange yellow green purple candies candies candies candies 16 9 7 15 15 Using the data compiled from the entire class, record the following information: Total 62 The total number of candies in the sample = ____1252_______ Number of red candies Proportion 251 0.200 Number of orange candies 238 0.190 Number of yellow candies 250 0.200 Number of green candies 249 0.199 Number of purple candies 264 0.211 Throughout this entire project, use decimals rounded to three places for all of your proportions. Do not use percents. The total number of candies in your own single 2.17-­‐‑ounce bag of Skittles = ___62____ The total number of bags in the sample collected by the entire class = ___21_____ The total number of candies in the sample collected by the entire class = ____1252_____ For the entire sample: 𝑥 = __59.6_____ (the mean number of candies per bag rounded to 1 decimal place) Method: Add all subtotals of candies per each bag together and divide by the total (21 bags) s = ___2.75____ (the std. deviation of the number of candies per bag rounded to two decimal places) Method: 5-­‐‑ number summary: (round to one decimal place where necessary) 51, 58, 60, 61, 64 (min, Q1, Q2 (median), Q3, max) Method: sort candy counts for each bag from lowest to highest and number sequentially) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 51 57 58 58 58 58 58 59 59 59 60 60 61 61 61 61 62 62 62 63 64 Minimum = (1) 51 Q1 = (25/100) x 21 = 5.25 (round to 6) = 58 Q2 (median) = (50/100) x 21 = 10.5 (round to 11) = 60 Q2 = (75/100) x 21 = 15.75 (round to 16) = 61 Maximum = (21) 64 1 Fill in the appropriate values on this page and keep it handy as you do your calculations. Quick Reference for Confidence Intervals For the interval estimate of the proportion of purple candies: n = __1252___ x = __264___ 𝑝 = __0.2108___ α = __0.05___ For the interval estimate of the mean number of candies in a bag: n = __21___ 𝑥 = __59.6___ α = __0.01___ s = 2.75 For the interval estimate of the standard deviation of the number of candies in a bag: n = __21___ s = __2.75___ α = __0.01___ 𝑋!! = ___37.566___ 𝑋!! = ___8.260___ Quick Reference for Hypothesis Tests For testing the claim that 20% of Skittles are green: n = __1252___ x = __249___ 𝑝 = __0.19888___ α = __0.01___ 𝐻! : _________p = 0.20____________ 𝐻! : _______p not equal to 0.20___________ For testing the claim that the mean number of Skittles in a 2.17-­‐‑oz. bag is 55: n = __21___ 𝑥 = __59.6___ α = __0.05___ 𝐻! : __________µ = 56___________ 𝐻! : _________µ not equal to 56___________ 2 Math 1040 Skittles Term Project – Part II Introduction: The goal of the project was to apply statistical methods learned in Math 1040 to better understand a real world situation, namely the variability in packaging of a commercial product, Skittles candy. Skittles can be purchased in single 2.17-­‐‑ounce bags. Each member of the class (21 of us) purchased one bag. Each bag contained a variable number of red, orange, yellow, green and purple candies. We each counted the number of each color of candy in our bag and provided these numbers to the instructor, who compiled a spreadsheet of the individual and combined data. From these data, each of us was to analyze the combined data for the class (21 bags), and to compare this to our own bag to learn about the variability in the packaging from bag-­‐‑to-­‐‑bag, and how this evens out when a large number of bags of Skittles are considered together. My initial hypothesis was that there would be very little variability between bags, but that proved not to be the case. There appeared to be quite a lot of variability both in the number of candies per bag, as well as the number of each color of candy. However, when all 21 bags were considered together, these differences seemed less impressive. Categorical Data: Colors The proportion of each color represented in the overall sample gathered by the class (21 bags) was first determined. This was calculated by dividing the total number of candies of each color by the total number of candies for the entire class (1252). As shown in the following Pie and Pareto Charts, these proportions ranged from 0.190 (19% of total) for orange, to 0.211 (21.1% of total) for purple. Visually, the differences between bars and the size of pie sections in these charts seem small, suggesting that the number of colors of candies was similar. 3 The similarity between the proportions of each color of candy in the overall data (from 21 bags) was surprising to me considering that the number and proportions of each color of candy in my own bag were quite different from each other and from the class mean, as shown by the following table and chart. However, with more careful inspection, the number of candies of each color, as well as the total number of candies in my bag was within the standard deviation of the class means, with the exception of the red and yellow candies, which were slightly above and below, respectively, the standard deviation of the mean values of the class values. Whether these exceptions were statistically significant is not clear. Color of candy Numbers of candies Proportion of total Class mean (s) My bag Class mean My bag Red 11.952 (3.008) 16 0.200 0.258 Orange 11.333 (3.039) 9 0.190 0.145 Yellow 11.905 (3.520) 7 0.200 0.113 Green 11.857 (3.395) 15 0.199 0.242 Purple 12.571 (2.993) 15 0.211 0.242 Total 59.619 (2.747) 62 4 Categorical Data (Numbers of candies): An assessment of the numbers of candies in each bag was made. Although each bag (supposedly) weighed exactly the same amount (2.17 ounces), there were some differences in the number of candies in each bag, although these differences were small. A total of 1252 candies represented the entire sample from the class (from 21 bags), for a mean of 59.6 candies per bag. However, the standard deviation for the number of candies per bag in the overall sample was quite small (2.75). The number of candies in my own bag was 62, which was within a standard deviation of the mean for the overall sample. The frequency distribution of the number of Skittles per bag roughly assumed a normal distribution from 56-­‐‑64 candies per bag, as shown in the table below and the chart (top of next page), with a single outlier. Frequency distribution # of Skittles per bag Frequency 50-­‐‑52 1 53-­‐‑55 0 56-­‐‑58 6 59-­‐‑61 9 62-­‐‑64 5 5 As shown in the Box Plot below, this outlier represented the minimum, at 51 candies in a bag. The 5-­‐‑number summary for the data was 51, 58, 60, 61 and 64. The first (Q1), second (Q2) and third (Q3) quartiles for the distribution of the number of Skittles per bag were tightly clustered from 58-­‐‑61. This shows that the differences for numbers of candies per bag were fairly small. Summary: The differences between numbers of candies per bag, and numbers of different colors in the overall sample from the class seemed quite small. At first glance, the number of 6 colors of candies in my bag of Skittles seemed quite different from that of the class as a whole. However, the number of candies per bag of each color fell within a standard deviation of the mean values of each color per bag for the overall sample (with the exception of red and yellow, which were slightly outside the standard distribution). There were some differences in the number of candies per bag, although the standard deviation for the overall sample was fairly small as well. Because each bag contains 2.17 ounces, it is possible that differences in numbers of candies per bag could be due to a slight difference in the weight/size of the candies, if the bags are packaged by weight. Alternatively, 2.17 ounces could be an average weight, and the actual weight of each bag could be slightly different. Reflection Quantitative (numerical) data consist of numbers representing counts or measurement. The numbers of Skittles in one bag would be an example. An individual’s weight and age would also be quantitative data. Using appropriate units of measurement such as dollars, hours, feet and meters is very important. Quantitative data can be either discrete or continuously. Categorical (qualitative) data consists of names or labels that are not numbers representing counts of measurements. Colors of Skittles would be categorical data. Other examples of categorical data include gender, political party affiliation, social security numbers, and sports jersey numbers. Graphs are commonly used in statistical analysis because they aid in the understanding and interpretation of data. Quantitative data is used to create scatter-­‐‑plots, time-­‐‑series plots, dot-­‐‑plots and stem-­‐‑plots. Categorical data is used in bar-­‐‑graphs, Pareto-­‐‑charts and pie charts. We use a Pareto chart and a pie chart in this project to help us describe and make sense of colors and skittles (categorical data). A histogram (graph of a frequency distribution) consists of a graph that is easier to interpret than a table of numbers. The horizontal scale (x-­‐‑axis) represents classes of quantitative data values and the vertical scale (y-­‐‑axis) represents frequencies. We make use of a histogram in our project to show a range of how many Skittles candies are contained in a sample of bags of Skittles and how many times (the frequency) that was observed from our data. The use of a histogram helps us to understand CVDOT: the center of the data, the variation, and the distribution and whether there are any outliers. Categorical data places individual data entries into groups and are typically summarized by reporting either the number of individuals or percentages of individuals falling into each category. Quantitative data can be analyzed by describing where the center of the data set is in various ways, with the mean and median being examples. 7 Math 1040 Skittles Term Project – Part III Confidence Interval Estimates A confidence interval is used in inferential statistics to measure the probability that a population parameter will fall between two set values. 95% and 99% confidence intervals are the two most commonly used. A 95% confidence interval, for example, means that if we used the same sampling method to collect samples of the same size as the one that we have analyzed and computed an interval estimate for each sample, we would expect the true population parameter to fall within the interval estimates 95% of the time. 8 Discussion and interpretation of the confidence interval assessments: Confident interval assessments were performed to determine the true proportion of Skittles that are purple. Based on these calculations, we are 95% confident that the interval from 0.188 to 0.233 actually contains the true value of the population proportion (p). This means that if we were to randomly select different samples of the same size (1252 candies) and construct corresponding confidence intervals, 95% of them would actually contain the true value of the population proportion p. Confident interval assessments were performed to determine the true mean number of Skittles per bag. Based on these calculations, we are 99% confident that the interval from 57.9 to 61.3 actually does contain the true value of the mean number of candies per bag in the population (µ). This means that if we were to randomly select different samples of the same size (21 bags of Skittles) and construct confidence intervals, 99% of them would actually contain the true value of the population mean µ. Confident interval assessments were performed to determine the true standard deviation for the number of Skittles per bag. Based on the results of our confident interval assessments, we have 98% confidence that the limit from 2.01 to 4.28 actually contains the true value for the standard deviation of the number of candies per bag in the population (σ). This means that if 9 we were to randomly select different samples of the same size (21 bags of Skittles) and construct confidence intervals, 98% of them would actually contain the true value of the population standard deviation σ. Hypothesis Tests Hypothesis testing refers to the formal procedures used in statistical analysis to accept or reject statistical hypotheses. A statistical hypothesis is an assumption about a population parameter. This assumption may or may not be true. The usual process of hypothesis testing consists of several steps. A basic outline is as follows: •
Formulate the null hypothesis (HO) and the alternate hypothesis (H1). •
Identify a test statistic that can be used to assess the truth of the null hypothesis. •
Draw a graph to include the test statistic, critical values, and critical region (if using the critical value method). •
Reject the null hypothesis (HO) if the test statistic is in the critical region. Fail to reject the null hypothesis if the test statistic is not in the critical region. •
Restate this previous decision in simple, non-­‐‑technical terms, and address the original claim. 10 Discussion and interpretation of hypothesis testing: We chose the critical value method to conduct hypothesis testing. We constructed a graph based on a fairly stringent significance value (.01) to test the null hypothesis that 20% of all Skittles candies are green. Since our test statistic of -­‐‑0.106 is in the rejected region (below the critical region between -­‐‑2.33 and 2.33), there is sufficient reason to warrant rejection of the claim (null hypothesis) that 20% of all Skittles candies are green. We used a somewhat more lenient significance level (.05) to test the null hypothesis that the mean number of all Skittles candies is 56. Based on the graph, the limits of our accepted region (critical region) were between -­‐‑2.086 and 2.086. Our test statistic is 5.999 is in the rejected region. Therefore, there is also sufficient evidence to warrant rejection of the claim (null hypothesis) that the mean number of candies in a bag of Skittles is 56. Reflection A. Interval estimates and hypothesis tests for population proportions require that the same conditions be met: •
The sample must consist of simple random observations. This condition is met by our sample. 11 •
The conditions for a binomial distribution must be satisfied. Our sample is binomial since the number of observations is fixed, the observations are independent, outcomes can be classified into two opposite categories (for example purple and non-­‐‑purple), and the probability of outcome is essentially the same in all observations. •
That condition that np > 5 and nq > 5 must both be satisfied. The term n is the number of trials, or in our case, candies (n = 1252) and the term p is the assumed population proportion (of being purple), which is 0.21. 1252 x 0.21 = 250, which is > 5. The value q would be much greater (the assumed population proportion of being non-­‐‑purple). Then nq = 1250 x .79 = 987.5, which is also > 5. So this condition for doing interval estimates for population proportions is also met. B. Interval estimates and hypothesis tests for population means require that the same conditions be met: •
The sample must consist of simple random observations. This condition is met by our sample. •
Either or both of the following must be satisfied: (1) The population must be normally distributed (based on the histogram shown in Part II, for numbers of candies per bag, the mean number of candies per bag is bell-­‐‑shaped, and thus normally distributed, but with one outlier); (2) The number of observations (n, sample size) must be > 30. This condition was not met, since n in this case is the number of bags of candies, which were 21. However, since the first condition was present (normally distributed), the overall condition was met. C. The conditions for doing interval estimates for population standard deviations are as follows: •
That the sample observations are a simple random sample (which is met by our sample). •
The population must be normally distributed (based on the histogram shown in Part II, for numbers of candies per bag, the mean number of candies per bag is normally distributed, but with one outlier). This requirement for a normal distribution is stricter here, since nonconforming data may result in large errors. However, the outlier is just one out of 21 bags of candy, so the condition of a normal distribution was likely met. There are several drawbacks of this study. First of all, the conditions that required for doing valid interval assessments and hypothesis testing for population means were met, but only technically. Among the conditions that must be met is that the number of observations (n, 12 sample size) must be > 30. This condition was not met, since n in this case is the numbers of bags of candies, which were 21. However, interval assessments and hypothesis testing for population means can still be done assuming that the sample is random (which it is) and that the sample assumes a normal distribution. The shape of the histogram was bell-­‐‑shaped, with one outlier, so the distribution would technically be considered normal. Although our data met the conditions for interval assessment and hypothesis testing for population means, this data would have been further strengthened by the inclusion of at least 9 more bags of Skittles. While a single outlier among 21 samples (bags of candies) does not preclude the data from being considered normal in distribution, it could slightly affect the population mean and standard deviation estimates. To determine this, the outlier could be eliminated from the sample and the confidence intervals recalculated to determine the degree to which this outlier affects the results. An additional limitation of the study is a fairly stringent significance level (.01) that was used to test the claim (null hypothesis) that 20% of all Skittles candies are green. If a more lenient significance level were used, it is possible that the null hypothesis would be accepted, but this would need to be determined. 13 Math 1040 Skittles Term Project – Part IV Reflections I entered this class at somewhat of a disadvantage, having been out of school for a long time, and never having felt that I had strong math skills. The applied mathematics required for this class have been challenging for me, but with repeat practice, I feel that my overall math skills have improved immensely. I have been greatly encouraged by my ability to master mathematics, both basic and more advanced. The acquisition of these mathematical skills has also lead to an improvement in my overall ability to think in an analytical manner. There is no question that the skills I gained in this statistics class will help me in my future studies. I am back in college after many years in the workforce as a radiologist assistant to obtain prerequisites necessary to apply to physician assistant school. These prerequisites required a fair amount of math (such as in chemistry). These courses are essentially completed now and I wish that I had had this statistics class before taking my chemistry class. Nonetheless, PA school usually awards a master’s level degree. This generally requires that a master’s research thesis be completed. The statistical skills acquired in this class will allow me to design a valid methodology for data gathering for this thesis. This class will help me analyze the data and form defensible conclusions. The specific coursework required for PA school also involves many disciplines, for example, pharmacology and epidemiology. In all of these, the synthesis of statistical data is a component. I feel that I will be better prepared for these classes having taken this statistics course. As a physician assistant, I will be required to interpret patient data, and make decisions regarding the management of patients. I will be required to present clear and accurate information to the supervising physician. This will involve the consideration of a wide variety of information from many sources. Whether a patient conforms to published groups of diagnostic categories, whether they fit the criteria for appropriateness for specific therapies, and whether they are responding to treatment is all related, in some manner, to statistics. The basic skills acquired in this class will help me to critically evaluate the literature or medical “claims” of drug companies. This statistics course will also help me to understand whether my own patient’s signs and symptoms fit a specific diagnosis, or whether they are actually improving or getting worse over time with treatment or conservative management. In short, the skills acquired will not only help me in course work, but will make me a better physician assistant. Specific parts of the project for this class have been very revealing for me. The importance of a random sample of sufficient size to allow for valid estimates to be made is a concept that has been new to me. The realization of the importance of this as a factor in statistical inference is 14 quite striking. Whether data conforms to a normal distribution is a concept to which I had no previous exposure. We are all bombarded, on a daily basis, through conversation and the media, to many “claims”. Just yesterday, for example, I was exposed to media making claims regarding public opinion surveys, breakthroughs in science and medicine, comparisons of the effectiveness of educational programs, and the existence of life on other planets! What I used to take at face value, I now regard with a much more critical perspective. In other words, because of this class, I am much more reluctant to simply believe what I read, and instead require a higher level of data analysis for me to accept a claim. When I am confronted with information that is unfounded or poorly supported from a statistical perspective, it is now more second nature to me to think about what would be required to convince me of something. In sort, this class has helped me to be a more responsible consumer and citizen. 15