Download Neutron Stars

Neutron Stars
Kostas Kokkotas
December 17, 2012
Kostas Kokkotas
Neutron Stars
Bibliography
I
Black Holes, White Dwarfs, and Neutron Stars S.L.Shapiro and S.A.
Teukolsky, see Chapters 2, 3, 8 and 9.
I
GRAVITY J.B. Hartle see Chapter 24
I
Duncan R. Lorimer, ”Binary and Millisecond Pulsars at the New
Millennium”, Living Rev. Relativity 4, (2001),
http://www.livingreviews.org/lrr-2001-5
I
D. R. Lorimer & M. Kramer; Handbook of Pulsar Astronomy; Cambridge
Observing Handbooks for Research Astronomers, 2004
Kostas Kokkotas
Neutron Stars
Neutron Stars: A Laboratory for Theoretical Physics
I
I
A neutron star is the collapsed core of a massive star left behind after a
supernova explosion. The original massive star contained between 8 and
25 M . (More massive stars collapse into black holes.) The remnant
neutron star compresses at least 1.4M into a sphere only about 10-16
km across.
This material is crushed together so tightly that gravity overcomes the
repulsive force between negatively charged electrons and positively
charged protons. The resulting structure of the star is complex, with a
solid crystalline crust about one kilometer thick encasing a core of
superfluid neutrons and superconducting protons. Above the crust exists
both an ocean and atmosphere of much less dense material.
Kostas Kokkotas
Neutron Stars
Pauli Principle
An isolated WD or NS cools down to zero temperature and it is the pressure
associated with matter at T = 0 that supports these stars against gravitational
collapse.
A simple but very important example of nonthermal source of pressure is the
Fermi pressure arising from the Pauli exclusion principle.
The Pauli exclusion principle:
I
restricts the quantum states allowed to half-integral spin particles (e, p,
n) known as fermions
I
prohibits any two fermions from occupying the same quantum state.
I
is crucial for the structure of atoms and their chemical properties
I
has the consequence that in the lowest-energy state of an atom, the
electrons are not in the lowest-energy level near the nucleus; instead they
are arranged in higher-energy-level shells.
I
it supports the outer electrons in an atom against the attractive electric
forces of nucleus.
Kostas Kokkotas
Neutron Stars
Electron degeneracy pressure
I
Electron degeneracy pressure is a force caused by the Pauli exclusion
principle, which states that two electrons cannot occupy the same
quantum state at the same time. This force often sets a limit to how
much matter can be squeezed together.
I
A material subjected to ever increasing pressure will become ever more
compressed, and for electrons within it, the uncertainty in position
measurements, ∆x, becomes ever smaller. Then, as dictated by the
Heisenberg’s uncertainty principle, ∆x ∆p ≥ ~2 , the uncertainty in the
momenta of the electrons, ∆p, becomes larger. Thus, no matter how low
the temperature drops, the electrons must be traveling at this
”Heisenberg speed”, contributing to the pressure.
I
When the pressure due to the “Heisenberg speed” exceeds that of the
pressure from the thermal motions of the electrons, the electrons are
referred to as degenerate, and the material is termed degenerate matter.
I
Electron degeneracy pressure will halt the gravitational collapse of a star if
its mass is below the Chandrasekhar Limit (1.44 M ). This is the
pressure that prevents a white dwarf star from collapsing.
Kostas Kokkotas
Neutron Stars
Maximum Mass of White Dwarfs I
White Dwarfs support themselves against gravity by the pressure of electrons
arising from the Pauli exclusion principle.
I
This pressure is called Fermi pressure and the corresponding
compressional energy is called Fermi energy.
I
A rough estimate of the maximum mass that can be supported against
gravity by Fermi pressure can be made by studying the Fermi energy of a
spherical configuration of radius R consisting of N electrons and N
protons (electrically neutral).
I
The heavier protons supply most of the mass and the lighter electrons
supply most of the pressure.
I
Since electrons exclude each other, we can think of each of them as
occupying a volume of characterisc size λ ∼ R/N 1/3
I
The Fermi momentum of electrons is
pF ∼ ~/λ ∼ N 1/3 ~/R
I
(1)
If the sphere is compressed, R shrinks, pF rises, the Fermi energy of the
electrons rises and work has to be done to make the compression.
Kostas Kokkotas
Neutron Stars
Maximum Mass of White Dwarfs II
If the compression has been carried out to the point that electrons become
relativistic with energies E = [pF2 + me2 c 2 ]1/2 c ≈ pF c. Then the total energy in
this approximation is:
EF ∼ N · (pF c) ∼ N 4/3 ~c/R .
(2)
The protons supply most of the gravitational energy EG , which is roughly
EG ∼ −G (mp N)2 /R
(3)
Both EF and EG vary as 1/R. For large N the total energy will be negative and
it will be energetically favorable for the configuration to collapse.
The critical N at which gravitational collapse is favored is
3/2
Ncrit ∼ ~c/Gmp2
∼ 2.2 × 1057
(4)
and the critical mass is1
Mcrit ∼ mp Ncrit ∼ 1.85M !
(5)
The exact solution of the maximum mass is called the Chandrasekhar mass and
it is about 1.4M !
1m
p
= 1.673 × 10−24 gr and M = 1.989 × 1033 gr
Kostas Kokkotas
Neutron Stars
Radius of White Dwarfs
The equilibrium masses associated with masses M approaching Mcrit is
determined by the onset of the relativistic degeneracy:
EF = pF c ≥ mc 2
(6)
where m refers to either electrons or neutrons. Then by using equations (1)
and (4) this condition gives
R≤
~
mc
~c
Gmp2
1/2
≈{
5.03 × 108 cm
2.74 × 105 cm
for
for
m = me
m = mn
(7)
Thus there are two distinct regimes of collapse:
I
one for densities above white dwarf values
I
and another for densities above nuclear densities
but in both cases M ∼ M .
2 Note:
2
mp = 1.242 × 10−52 cm, h = 2.612 × 10−66 cm2 & me = 6.764 × 10−56 cm.
Kostas Kokkotas
Neutron Stars
Maximum Mass of White Dwarfs III
An ideal fermion gas is described by Fermi-Dirac statistics (if bosons then
Bose-Einstein statistics) with distribution function (µ: chemical potential)
1
e (E −µ)/kT + 1
For low particle densities and high temperatures it reduces to
Maxwell-Boltzmann distribution f (E ) = e (µ−E )/kT with f (E ) 1.
f (E ) =
I
I
(8)
For completely degenerate fermions (T → 0 i.e. µ/kT → ∞) µ becomes
the Fermi energy, EF = [pF2 c 2 + me2 c 4 ]1/2 and
f (E ) = {
1
0
E ≤ EF
E > EF
(9)
That means that there is only one electron per allowed quantum state
with momentum p up to a maximum value the pF (Fermi momentum).
The number density of electrons will be:
Z pF
8π
1
2
4πp 2 dp = 3 pF3 =
x3
ne = 3
~ 0
3~
3π 2 λe
(10)
where x = pF /me c is the dimensionless Fermi momentum and λe = ~/me c is
the electron Compton wavelength.
Kostas Kokkotas
Neutron Stars
Maximum Mass of White Dwarfs IV
The pressure will be Pe ≈ 13 ne < pv > where v = pc 2 /E is the velocity and
the energy density e ≈ ne E or analytically (why?):
Z pF
me c 2
1 2
p2 c 2
4πp 2 dp =
Pe =
φ(x)
2 4 1/2
3
2
2
3 ~ 0 (p c + me c )
λ3e
=
e
=
1.42 × 1025 φ(x) dyne/cm2
Z pF 1/2
me c 2
2
p 2 c 2 + me2 c 4
4πp 2 dp =
χ(x)
3
h 0
λ3e
(11)
(12)
where
φ(x) =
io
h
1 n
x(1 + x 2 )1/2 (2x 2 /3 − 1) + ln x + (1 + x 2 )1/2
→{
2
8π
χ(x) =
h
io
1 n
x(1 + x 2 )1/2 (1 + 2x 2 ) − ln x + (1 + x 2 )1/2
→{
2
8π
Kostas Kokkotas
Neutron Stars
x5
15π 2
x4
12π 2
x3
3π 2
x4
4π 2
x 1
x 1
x 1
x 1
Maximum Mass of White Dwarfs V
Even if degenerate electrons contribute most of the pressure, the density is
usually dominated by the rest-mass of the ions. The density is
X
ne mB
ρ0 =
ni mi ≡ nmB =
= µe mu ne = 0.974 × 106 µe x 3 g/cm3
(13)
Ye
i
where mi is the mass of ion species i, mB is the mean baryon density, Ye is the
mean number of electrons per baryon, mu = 1.66 × 10−24 g is the atomic mass
unit and µe = mB /mu Ye is the mean molecular weight per electron.
Equations (11) and (13) provide in a parametric form the ideal degenerate
equation of state (EoS) P = P(ρ0 ) 3 .
If we use a polytropic form for the (EoS) P = K ρΓ0 where K and Γ are
constants we get two limiting cases:
I Non-relativistic electrons ρ 106 g/cm3 ,x 1
Γ=
I
5
,
3
32/3 π 4/3
~2
= 1.004 × 1013 µ−5/3
cgs
e
5/3 5/3
5
me mu µe
(14)
Extremely relativistic electrons ρ 106 g/cm3 , x 1
Γ=
3ρ
K =
4
,
3
K =
31/3 π 2/3
~c
= 1.24 × 1015 µ−4/3
cgs
e
4/3 4/3
4
m u µe
(15)
= ρ0 + e /c 2 is the total energy density but the last term e /c 2 is negligible.
Kostas Kokkotas
Neutron Stars
The Tolman-Oppenheimer-Volkov (TOV) Solution
The energy momentum tensor for a perfect fluid is:
T µν = (ρ + p)u µ u ν − g µν p
where
uµ =
dx µ
ds
Then the law for conservation of energy and momentum leads to:
T µν ;ν = g µν ∂ν p + [(p + ρ)u µ u ν ];ν + (ρ + p)Γµ νλ u µ u λ = 0
(16)
For a spherically symmetric and static solution
ds 2 = e ν(r ) dt 2 − e λ(r ) dr 2 − r 2 dθ2 + sin2 θdφ2
the fluid velocity is: u µ = (e −ν/2 , 0, 0, 0) and thus (16) becomes
T µν ;ν = ∂ν pg µν + (ρ + p)Γµ 00 u 0 u 0 = 0
where Γµ 00 = − 21 g µν g00,ν = − 12 e ν ν 0
Kostas Kokkotas
Neutron Stars
(17)
TOV - II
...multiplying with gµλ we get
1
∂λ p = − (ρ + p) ∂λ ν
2
⇒
dp
1
dν
= − (ρ + p)
dr
2
dr
(18)
which is the relativistic version of the equations for hydrodynamical equilibrium,
since in the Newtonian limit g00 = e ν ≈ 1 + 2U and ρ p which leads to:
∂p
∂U
= −ρ
∂r
∂r
Still we need to find a way, via Einstein’s equations
1
Rµν = −8π Tµν − gµν Tλλ
2
(19)
(20)
to estimate ν(r ) in the same way that we need to solve Poisson equation to
estimate the gravitaional potential U.
Kostas Kokkotas
Neutron Stars
TOV - III
{θθ}
:
{rr }
:
{tt}
:
h
i
r
1 − e −λ 1 + (ν 0 − λ0 ) = −4πr 2 (ρ − p)
2
(ν 0 )2
ν 00
ν 0 λ0
λ0
+
−
−
= 4πe λ (ρ − p)
2
4
4
r
(ν 0 )2
ν 00
ν 0 λ0
ν0
+
−
+
= −4πe λ (3ρ + p)
2
4
4
r
which leads to the following ODE
0
re −λ = 1 − 8πρr 2 leading to
e λ(r ) = (1 − 2M/r )−1
(21)
(22)
(23)
r λ0 + e λ − 1 = 8πe λ r 2 ρ or
Z
where
M(r ) = 4π
r
ρ(r 0 )r 02 dr 0
(24)
0
which together with (18) give
M + 4πr 3 p
dp
= −(ρ + p)
dr
r (r − 2M)
Kostas Kokkotas
or
dν
M + 4πr 3 p
=2
.
dr
r (r − 2M)
Neutron Stars
(25)
TOV - IV : A uniform density star
For the special case ρ = const there is an analytic solution. For example the
mass function will become:
M(r ) =
4 3
πr ρ
3
for
r ≤R
and
M(r ) =
4
πR 3 ρ
3
for
r ≥R
The we get:
(1 − 2Mr 2 /R 2 )1/2 − (1 − 2M/R)1/2
p
=
.
ρ
3(1 − 2M/R)1/2 − (1 − 2Mr 2 /R 3 )1/2
(26)
But substituting the above relations in (18) we get an analytic solution for g00
i.e.
1/2
1/2
3
2M
1
2Mr 2
e ν/2 =
1−
−
1−
.
(27)
2
R
2
R3
Maximum allowed mass when p(r = 0) → ∞ :
M
4
=
R
9
Kostas Kokkotas
Neutron Stars
Spherical Relativistic Stars
The equations of structure for a spherical relativistic star are:
dm
dr
dP
dr
dν
dr
=
4πr 2 ρ
(28)
3
=
=
m + 4πr P
r (r − 2m)
1 dP
−
ρ + p dr
−(ρ + p)
(29)
(30)
together with and EoS P = P(ρ) and an equation for the metric function λ(r )
i.e. e −λ(r ) = 1 − 2m/r . If we move from geometrical units back to the cgs units
G
G
G
2
m, ρ → 2 ρ, P → 4 P and ν(r ) → 2 Φ
c2
c
c
c
we get the following equations describing a spherical star in hydrostatic
equilibrium in the non-relativitic limit
m→
dm
dr
dP
dr
dΦ
dr
=
4πr 2 ρ
=
−ρ
=
Kostas Kokkotas
Gm
r2
1 dP
Gm
−
= 2
ρ dr
r
Neutron Stars
(31)
(32)
(33)
(34)
Polytropes I
The ideal Fermi gas EoS reduces to simple polytropic form P = K ρΓ0 in the
limiting cases of extreme non-relativistic (Γ = 5/3) and ultrarelativistic
electrons (Γ = 4/3). Equilibrium configurations with such an EoS are called
polytropes and herey are quite simple to analyze.
The hydrostatic equilibrium equations (32) and (33) can be combined to give
1 d r 2 dP
= −4πG ρ
(35)
r 2 dr ρ dr
if we substitute P = K ρΓ0 , and we write Γ = 1 + 1/n (n is called polytropic
index) we can get a dimensionless form of this equation the so called
Lane-Emden equation
1 d
2 dθ
ξ
= −θn
(36)
ξ 2 dξ
dξ
where we have made the following substitutions
#
"
1/n−1 1/2
(n + 1)K ρc
(37)
ρ = ρc θn , r = aξ, a =
4πG
where ρc = ρ(r = 0) is the central density. While the boundary conditions are
θ(0) = 1 ,
Kostas Kokkotas
and
θ0 (0) = 0 .
Neutron Stars
(38)
Polytropes II
Lane-Emden equation can be easily integrated numerically starting at ξ = 0
with the BC (38). For n < 5 the solution decreases monotonically and has a
zero at finite value ξ = ξ1 i.e. θ(ξ1 ) = 0 which corresponds to the surface of
the star, where p = ρ = 0. Thus we get:
R
=
aξ1 =
Z
M
=
=
(n + 1)K
4πG
1/2
ρc(1−n)/2n ξ1
R
(39)
3/2
(n + 1)K
ρ(3−n)/2n
ξ12 |θ0 (ξ1 )|
c
4πG
0
n/(n−1)
(n + 1)K
(3−n)/(1−n) 2 0
4πR (3−n)/(1−n)
ξ1
ξ1 |θ (ξ1 )|.
4πG
4πr 2 ρdr = ... = 4π
(40)
(41)
For the special cases that we are interested:
5
,
3
4
Γ= ,
3
Γ=
3
,
2
ξ1 = 3.65375,
ξ12 |θ0 (ξ1 )| = 2.71406
(42)
n = 3,
ξ1 = 6.89685,
ξ12 |θ0 (ξ1 )| = 2.01824
(43)
n=
Kostas Kokkotas
Neutron Stars
Polytropes II
Figure: θ(ξ) for n = 0, 1, 2, 3, 4 and 5
Kostas Kokkotas
Neutron Stars
Maximum Mass of White Dwarfs : Chandrasekhar limit
For low-density white dwarfs Γ = 5/3 we get:
−1/6 µe −5/6
ρc
km (44)
R = 1.122 × 104
3
2
106 g/cm
−3 1/2 µe −5
ρc
µe −5/2
R
M = 0.5
M
=
0.7
M (45)
3
4 km
6
2
10
2
10 g/cm
For the high-denity case Γ = 4/3 we get:
−1/3 µe −2/3
ρc
R = 3.35 × 104
km
3
2
106 g/cm
2
2
M
M = 1.457
µe
(46)
(47)
Note that M is independent of ρc and R in the ultra-relativistic limit. Thus as
ρc → ∞, the electrons become more and more relativistic throughout the star,
then R → 0 and the mass asymptotically will be given by equation (47).
The mass limit (47) is called Chandrasekhar limit (MCh = 1.457M ) and is the
maximum possible gas of a white dwarf. For cold perfect gas the dependence
of MCh on composition is contained entirely in µe = mB /mu Ye = A/Z which is
the mean molecular weight per electron, for He : A = 4 &Z = 2.
Kostas Kokkotas
Neutron Stars
Neutron Stars I
The above results can be easily scaled to determine the equation of state of an
arbritrary species i of ideal fermions. For pure neutrons we get:
n =
mn c 2
χ(xn ) = 1.625 × 1038 χ(xn )
λ3n
(48)
where xn = pF /mn c.
ρ0 = mn nn =
mn 1 3
xn = 6.107 × 1015 xn3 g/cm3
λ3n 3π 2
(49)
If we use a polytropic form for the equation of state (EoS) P = K ρΓ0 we get for
the two limiting cases:
I Non-relativistic neutrons ρ 6 × 1015 g/cm3 , x 1
Γ=
I
5
,
3
K =
32/3 π 4/3 ~2
= 5.38 × 109 cgs
8/3
5
mn
(50)
Extremely relativistic neutrons ρ 6 × 1015 g/cm3 , x 1
Γ=
4
,
3
K =
31/3 π 2/3 ~c
= 1.23 × 1015 cgs
4/3
4
mn
(51)
Notice that in this case the mass density ρ = n /c 2 is due entirely to neutrons
and greatly exceeds ρ0 whenever the neutrons are extremely relativistic.
Kostas Kokkotas
Neutron Stars
Neutron Stars II
Low density neutron stas with the ideal neutron gas equation of state can be
approximated by n = 3/2 Newtonian polytropes. From eqns (39) & (41) we
get:
−1/6
ρc
km
1015 g/cm3
1/2
ρc
M
M = 1.102
1015 g/cm3
R = 14.64
(52)
(53)
Thus there is no minimum neutron star mass i.e. M → 0, ρc → 0 and R → ∞.
In nature, of course, neutrons become unstable to β-decay at low densities.
Kostas Kokkotas
Neutron Stars
Neutron Stars III : Nuclear Density
In neutron stars the density is higher than the nuclear density!
The maximum value for the momentum of a neutron will be ∆p ∼ mp c. Then
the uncertainty principle ∆p ∆x ∼ ~ suggests that
∆x ∼
~
∼ 10−13 cm
mp c
(54)
actually the exact value is ∆x ∼ 1.8 × 10−13 cm i.e. the neutrons “touch” each
other.
The number density will be
n∼
1
≈ 1.7 × 1038 cm−3
∆x 3
(55)
and the density will be
ρn = mp n ≈ 2.8 × 1014 g /cm3
In neutron stars the average density is higher than this value.
Kostas Kokkotas
Neutron Stars
(56)
Neutron Stars IV : Composition
I
NS’s surface is believed to consist of a very thin fluid/gas atmosphere.
I
Beneath that, the outer crust will typically consist of a lattice of 56
26 Fe.
The pressure in this region is mainly provided by the iron lattice.
I
At higher densities more and more electrons will become free and the
pressure will increasingly be due to the degenerate electron gas. In the
region were ρ 106 g/cm3 the free electrons are non-relativistic and the
compressibility index
γ = (ρ + p)/pdp/dρ
I
As we go further towards the center of the star the electrons become
increasingly relativistic and γ → 4/3.
I
At a density of about 106 g/cm3 the electrons and protons start
recombining in inverse β-decay e − + p → n + νe thus forming increasingly
neutron rich nuclei.
I
At ρ ∼ 3 × 1011 g/cm3 the nuclei gets unstable and the free neutrons are
emitted. This is called the ”neutron drip” region and here the EoS will
become very soft (low compressibility index).
takes the value γ = 5/3.
Kostas Kokkotas
Neutron Stars
Neutron Stars IV : Composition
I
As we move towards the center, the matter consists mostly of free
neutrons and small abundances of free protons, electrons and muons. The
pressure will be provided mainly by the degenerate neutrons and the
compressibility index will decrease from the non-relativistic value 5/3 to
the relativistic 4/3.
I
The neutrons become superfluid at some point in the neutron star.
I
If no phase transitions occur the EoS will approach p → ρ/3
I
The actual EoS in these ultra high densities is highly unknown e.g. there
might exists a quark-gluon plasma, kaon condensates and other exotic
states of matter etc
Kostas Kokkotas
Neutron Stars
Neutron Stars V
Figure: Schematic cross section of a neutron star, showing the outer crust
consisting of a lattice of nuclei with free electrons, the inner crust which also
contains a gas of neutrons, the nuclear “pasta” phases, the liquid outer core,
and the possibilities of higher-mass baryons, Bose-Einstein condensates of
mesons, and possible quark matter in the inner core.
Kostas Kokkotas
Neutron Stars
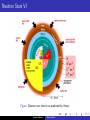
Neutron Stars VI
Figure: Neutron star interior as predicted by theory
Kostas Kokkotas
Neutron Stars
Neutron Stars VII
Figure: Mass-radius curve for HWW EoS configurations. The curve is
parametrized by central density measured in gr/cm3 . At the extrema (max or
min) the configuration becomes unstable/stable for increasing central density.
Kostas Kokkotas
Neutron Stars
Neutron Stars VIII
Figure: Mass-radius relationship of neutron stars and strange stars. The
strange stars may be enveloped in a crust of ordinary nuclear matter whose
density is below neutron drip density.
Kostas Kokkotas
Neutron Stars
Neutron Stars: History
I
Walter Baade and Fritz Zwicky from CalTech first predicted the
existence of neutron stars in 1934, but they were not discovered
until over 30 years later.
I
Pulsars are a special category of spinning neutron stars, discovered
in 1967 by Jocelyn Bell, an astronomy graduate student working
with Prof. Antony Hewish at Cambridge. Pulsars derive their name
from ”pulsating radio sources” because they were first observed at
radio wave frequencies. Hewish won the 1974 Nobel Prize in Physics
along with Sir Martin Ryle for their ”pioneering discoveries in radio
astrophysics.” Hewish was cited for his ”decisive role in the
discovery of pulsars.”
Kostas Kokkotas
Neutron Stars
Neutron Stars: Supernovae
A supernova explosion is usually associated with the formation of black holes
and neutron stars.
I
Young stars are hydrogen, and the nuclear reaction converts hydrogen to
helium with energy left over. The left over energy is the star’s
radiation–heat and light.
I
When most of the hydrogen has been converted to helium, a new nuclear
reaction begins that converts the helium to carbon, with the left over
energy released as radiation.
I
This process continues converting the carbon to oxygen to silicon to iron.
Nuclear fusion stops at iron.
I
A very old star has layers of different elements. The outer layers of
hydrogen, helium, carbon, and silicon are still burning around the iron
core, building it up.
I
Eventually, the massive iron core succumbs to gravity and it collapses to
form a NS. The outer layers of the star fall in and bounce off the neutron
core which creates a shock wave that blows the outer layer outward.
I
This is the supernova explosion.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Supernovae (sequence of events)
I
I
I
I
Within about 0.1 sec, the core collapses.
After about 0.5 sec, the collapsing envelope interacts with the outward
shock. Neutrinos are emitted.
Within 2 hours, the envelope of the star is explosively ejected. When the
photons reach the surface of the star, it brightens by 8 orders of mag.
Over a period of months, the expanding remnant emits X-rays, visible
light and radio waves in a decreasing fashion.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Modelling
I
Stars more massive than ∼ 8M end in core collapse ( 90% are stars
with masses ∼ 8 − 20M ).
I
Most of the material is ejected
I
If M > 20M more than 10 % falls back and pushes the PNS above
the maximum NS mass leading to the formation of BHs (type II
collapsars).
I
If M > 40M no supernova is launched and the star collapses to
form a BH (type I collapsars)
I
Formation rate: 1-2 per century / galaxy
I
5-40% of them produce BHs through the fall back material
I
Limited knowledge of the rotation rate! Initial periods probably
< 20ms. Maybe about 10% of pulsars are born spinning with
millisecond periods.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Maximum Mass I
The mass of a stable neutron star can be estimated by using the following
assumptions (Rhoades & Rufinni 1974):
1. GR is the correct theory of gravity and Tolman-Oppenheimer-Volkov
equations describe the equilibrium structure.
2. The EoS satisfies the “microscopic stability” condition dP/dρ ≤ 0. If this
condition is violated small elements of matter will spontaneously collapse.
3. The EoS should satisfy the causality condition dP/dρ ≤ c 2 i.e. the speed
of sound is less than the speed of light.
4. The EoS below some critical density ρ0 is known
The most fundamental from the above statements is the 3rd one which leads
into P = P0 + (ρ − ρ0 )c 2 for ρ ≤ ρ0 .
Rhoades & Rufinni adopted ρ0 = 4.6 × 1014 g/cm3 and one of the very first EoS
(the Harisson-Wakano) and they got
Mmax ≈ 3.2
4.6 × 1014 g/cm3
ρ0
Kostas Kokkotas
Neutron Stars
1/2
M
(57)
Neutron Stars: Maximum Mass II
Actually for uniform density stars one can proves that the maximum mass can
be derived by studying the stability. That is by extremising the energy (for a
fixed number of baryons):
2 ∂M = 0 and ∂ M > 0
(58)
∂χ ∂χ2 A
A
where M is the stellar mass, A is the total baryon number and sin2 χ = 2M/R.
These condition imply that there is a critical adiabatic index
(3ζ + 1 ζ + 1
∂ ln P
ρ dP
Γ≡
= 1+
> Γc (χ) = (ζ+1) 1 +
tan2 χ − 1
∂ ln n
P dρ
2
6ζ
(59)
where
6 cos χ
ζ(χ) ≡
−1
9 cos χ − 2 sin3 χ/(χ − sin χ cos χ)
in the Newtonian limit
4
89 M
+
3
105 R
∼ 3.6M .
Γc =
and the maximum mass is : Mmax
Kostas Kokkotas
Neutron Stars
(60)
Neutron Stars: Maximum Mass III
Figure: The stability domain in the uniform-density approximation. The curve
separating the stable and unstable regions is the function Γc given by eqn (59).
The dashed line shows the adiabatic index of a free neutron gas.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Maximum Rotation
The shortest period for a rotating star occurs when it is rotating at break-up
velocity called also Kepler limit:
Ω2 R ∼
GM
R2
(61)
where Ω is the angular velocity of rotation. This can be written also in terms of
the mean density ρ as:
Ω2 ∼ G ρ
(62)
the universal relation between dynamical time-scale and density for a
self-gravitating system.
I
For mean densities of 108 g/cm3 (white dwarfs) this relation gives a period:
P=
I
2π
≥ 1 sec
Ω
For mean densities of 1014 g/cm3 (neutron star) this relation gives a
period:
2π
P=
≥ 1 msec
Ω
Kostas Kokkotas
Neutron Stars
Neutron Stars: Magnetic Field
During the collapse if we assume that the initial angular momentum and
magnetic flux are conserved we will end up in a neutron star with msec period
and magnetic field of the order of 1012 G.
I
Conservation of angular momentum
2
MR Ω =
2
MRNS
ΩNS
⇒ PNS = P
RNS
R
2
∼ 0.5ms
(63)
for P ∼ 1 month and R/RNS ∼ 7 × 105 .
I
Conservation of magnetic flux
2
R 2 B = RNS
BNS ⇒ BNS = B
R
RNS
2
for initial B ∼ 100 Gauss.
Kostas Kokkotas
Neutron Stars
∼ 5 × 1012 Gauss
(64)
Neutron Stars: Pulsars I
I
From our earthly vantage point, pulsars appear to pulse with light with
each rotation.
I
Their light, like a lighthouse beam, sweeps across the Earth.
I
Some pulsars emit visible light, X-rays, and even gamma-rays.
I
All pulsars are NS, but (so far as we know) not all NS are pulsars.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsar Observation
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars - The magnetic dipole model
The pulsar emission is derived from the kinetic energy of a rotating NS.
In the oblique rotator model, it is assumed that the NS rotates uniformly in
~ oriented at
vacuo at a frequency Ω and possess a magnetic dipole moment m
an angle α to the rotation axis.
~ by
A dipole magnetic field at the pole of the star BP is related to m
|~
m| =
1
BP R 3
2
R is the radius of the star
(65)
The radiation at infinity due to the time-varying dipole moment will be:
Ė = −
B 2 R 6 sin2 α 4
2 ~ 2
|m̈| = ... = − P
Ω
3
3c
6c 3
(66)
The energy carried away by the radiation originates from the rotational kinetic
energy of the NS E = I Ω2 /2, where I is the moment of inertia. Thus
Ė = I ΩΩ̇
i.e. the pulsar slows down. The characteristic age T of pulsar is:
Ω
6Ic 3
T =−
= 2 6 2
BP R sin αΩ20
Ω̇ 0
Kostas Kokkotas
Neutron Stars
(67)
(68)
Neutron Stars: Pulsars - The magnetic dipole mode
By integration we get the initial angular velocity
1/2
Ω2i t
Ωi = Ω 0 1 + 2 2
Ω0 T
where t is the present age of the pulsar given by:
T
Ω2
T
t=
1 − 02 ≈
2
2
Ωi
(69)
(70)
For the Crab pulsar this method predicts 1260 yr while the true is 947 yr.
The magnetic field strength can be estimated
√
p
6c 3 I p
19
P
Ṗ
≈
5.2
×
10
P Ṗ Gauss
(71)
BP =
2πR 3 sin2 α
For a typical NS (M = 1.4M , R = 12km and I = 1045 g/cm2 ) we get
E = 1.8 × 1049 erg ,
Ė = 4.6 × 1038 erg/s
(72)
from the above estimation we get an approximate value for the magnetic field
strength of the Crab pulsar.
BP = 4.4 × 1012 G
which is the same as the predicted value earlier.
Kostas Kokkotas
Neutron Stars
(73)
Neutron Stars: Pulsars - Ṗ vs P Diagram
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars - Ṗ vs P Diagram
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars - Braking index
If the pulsar slowdown follows a power-law then we can write
Ω̇ ≈ Ωn
(74)
the parameter n is called the braking index and for the magnetic dipole model
n = 3.
In general we can define
ΩΩ̈
n≡
(75)
Ω̇2
which suggests that the braking index can be measured directly from the pulsar
frequency and its derivative.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars and Gravitational Radiation
Slight deformations of a pulsar (eg deformed ellipsoid) can be sources of GWs
and account for their slow down. The energy loss in GW is:
32 G 2 2 6
I Ω
(76)
ĖGW = −
5 c5
Small ellipticities can generate GW emission. Magnetic fields of the order of
1015 -1016 Gauss can generate such ellipticities.
The deceleration law for constant is
ĖGW = I ΩΩ̇ ∼ Ω6
By integration we get the initial angular velocity
1/4
Ω4i t
Ωi = Ω0 1 + 4 4
Ω0 TGW
where t is the present age of the pulsar given by:
Ω4
TGW
TGW
t=
1 − 04 ≈
4
4
Ωi
(77)
(78)
(79)
For the Crab pulsar this method predicts 620 yr while the true is 947 yr i.e.
gravitational radiation cannot alone be responsible for the Crab slowdown.
A combination of gravitational and magnetic dipole radiation can be found
which may give both the correct age and the observed pulsar deceleration rate.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars - The Aligned Rotator
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars - The Aligned Rotator
I
I
I
I
I
I
I
Goldreich-Julian(1969) suggested that strong E-fields parallel to the
surface will rip off charged particles creating a dense magnetosphere
The charged particles in the magnetosphere within the light cylinder, must
corotate with the pulsar.
The light cylinder extends out to the distance at which the corotation
velocity attains the speed of light. The corotation radius is thus given by
c
Rc ≡
= 5 × 104 P km
(P : is the pulsar period in sec)
(80)
Ω
As the particles approach Rc in the equatorial plane, they become highly
relativistic.
Whether or not the dipole field is aligned with the rotation axis plasma
near the pulsar can in principle carry away sufficient angular momentum
and energy to supply the necessary and energy to supply the necessary
braking torque.
B2 R6
The energy loss will be dictated again by Ė = − Pc 3 Ω4 which leads again
to a breaking index n = 3.
Particles accelerate along the B-field lines. Relativistic e − emit high
energy EM radiation (γ-rays) which may disintegrate γ → e − + e + and
this goes on!
Kostas Kokkotas
Neutron Stars
Neutron Stars: Pulsars II
Pulsars are divided into two main categories, isolated pulsars and binary
pulsars.
I
Isolated pulsars (which include most radio pulsars) produce radiation
primarily through their rotation, as they gradually slow down and
cool off. Their light is generated by electrons caught in the pulsar’s
strong magnetic field, concentrated and emitted near the magnetic
poles. Thus, much of an isolated pulsar’s visible energy is funneled
from the rotating magnetic pole region. The precise location of the
beam is debated.
I
Pulsars in Binarys are those in orbit with a companion star, most
often hydrogen-burning stars like our Sun. Such a pulsar can pull
over, or accrete, matter from its stellar companion as their orbits
bring these objects in close contact with each other. The violent
accretion process can heat the gas being transferred and produce
X-rays. The X-rays from this matter, under the influence of magnetic
fields, can also appear to pulsate at the pulsar’s rotation rate.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Significant Pulsars
I
I
I
I
I
I
I
I
I
I
I
The first radio pulsar, CP 1919 (now known as PSR 1919+21), with a
pulse period of 1.337 seconds and a pulse width of 0.04 second, was
discovered in 1967
The first binary pulsar, PSR 1913+16, whose orbit is decaying at the
exact rate predicted due to the emission of gravitational radiation by
general relativity
The first millisecond pulsar, PSR B1937+21
The brightest millisecond pulsar, PSR J0437-4715
The first X-ray pulsar, Cen X-3
The first accreting millisecond X-ray pulsar, SAX J1808.4-3658
The first extrasolar planets to be discovered orbit the pulsar PSR
B1257+12
The first double pulsar binary system, PSR J0737?3039
The magnetar SGR 1806-20 produced the largest burst of energy in the
Galaxy ever experimentally recorded on 27 December 2004
PSR J1748-2446ad, at 716 Hz, the pulsar with the highest rotation speed.
PSR J0108-1431, the closest pulsar to the Earth. It lies in the direction of
the constellation Cetus, at a distance of about 86 parsecs.
Kostas Kokkotas
Neutron Stars
Neutron Stars: X-ray binaries
I
Binary pulsars are often called X-ray binaries. The flow of matter from the
stellar companion, the accretion disk, also glows in X-rays owing to its
high temperature. While some X-ray binaries are steady X-ray sources,
others are bright only for a few weeks or months at a time, lying dormant
for years between outbursts. The X-ray sky is thus highly variable, unlike
the visible night sky.
I
X-ray binaries were first discovered by R. Giacconi and collaborators in the
early ’60s, with their binary nature established in the early ’70s by
Giacconi and others. Giacconi was awarded the 2002 Nobel Prize in
Physics for ”pioneering discoveries in astrophysics, which have led to the
discovery of cosmic X-ray sources.”
Kostas Kokkotas
Neutron Stars
Neutron Stars: Cannibals
I
The process of accretion can speed up the spin of a binary pulsar,
since the high-velocity accreting material hits the pulsar at a grazing
angle, constantly spinning it faster.
I
Rotation rates for such accretion-powered pulsars can reach
hundreds of Hz, nearly kHz (millisecond pulsars)
I
The transfer of material onto the neutron star also slowly
cannibalizes the stellar companion so that, over millions of years,
enough matter is accreted away to completely whittle away a once
healthy star.
I
There are pulsars orbiting stars with as little as 10 Jupiter masses.
One well-known example is the pulsar B1957+20, known as the
”Black Widow” pulsar, which is emitting a stream of high-energy
radiation that will soon blow away its now feeble companion so that
no trace of this star remains.
Kostas Kokkotas
Neutron Stars
Neutron Stars: Millisecond Pulsars
I
I
I
There are many known isolated millisecond pulsars detected in the
radio-wave regime. The fastest known is the pulsar PSR J1748-2446ad,
spinning at an astonishing 716 Hz (2nd 649Hz and 3rd at 588 Hz).
It is believed that these isolated millisecond radio pulsars were once X-ray
binary millisecond pulsars that accreted material, spun up, and
cannibalized their companions.
This link was first confirmed in 1998 when scientists using the Rossi X-Ray
Timing Explorer found that the X-ray binary millisecond pulsar SAX
J1808.4-3658 was accreting matter from a companion with only 0.05M .
Kostas Kokkotas
Neutron Stars
Neutron Stars: Population
I
The Galaxy is thought to contain about 100,000 pulsars, yet about two
thousand are known.
I
Only a small fraction of these are millisecond pulsars.
I
Isolated pulsars are hard to find because they are dim.
I
X-ray binary millisecond pulsars are discovered when they flare up in a
rare, sporadic accretion event that lasts only a few weeks. In many X-ray
binaries, however, the accreted material on the neutron star is occasionally
consumed in a violent thermonuclear explosion that sweeps across the
surface, generating a bright burst of X-rays lasting a few seconds.
I
Using the Rossi Explorer in 1996 discovered rapid X-ray flickering during
some of these explosions, called ”X-ray burst oscillations,” and suggested
that this flickering might offer another way to measure the spin rates of
neutron stars. An advantage of this approach is that burst oscillations are
bright and fairly common.
Kostas Kokkotas
Neutron Stars