Download lecture 7 OPL and interference

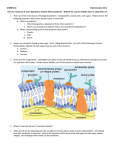
Optical path length
opl = path length x η
Δopl = Δ path length x Δη
δ (phase shift) = 2π x Δopl / λ
degs. rads.
90o
0π
.5 π
180o
1π
270o
360o
1.5π
2π
0o
90o
0o
180o 360o
270o
How far out of
phase have these
2 waves become?
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
One full wavelength λ, one full
cycle, 360 degrees or 2 π
Combine black ray or wave with grey one and derive resultant (or
only relative phase and amplitude changes. Remember, this ene
redistributed to another place in space (where is not always obvio
Relative phase difference of
1/4 λ or 1/2 π.
Relative phase difference of
1/2 λ of π.
resultant energy in space
In a phase contrast microsccope, a ring at the back plane of the
rays (those that do not interact with the specimen) by one quarte
combined with a ~one quarter λ retardation at the sample leads t
interference at the image plane; differences in phase shifting pro
amplitude differences.
One full wavelength λ, one full
cycle, 360 degrees or 2 π
Relative phase difference of
1 λ or 2π.
resultant reflection
1
2r
2t
polym
3r 4
glass,
3t
Solve for followin
resultant transmitted
Wavelengths of li
Wavelengths of li
Wavelengths of li
Wavelengths of li
t-transmitted, r-reflected
1 is a ray of white light
When 1 hits polymer surface, it is split into 2t and 2r, 2r is phase shifted relative to 2t by 1/2 λ or π (low to high η
interface).
2t continues on and is split into 3t and 3r at the glass surface, there is no phase shift with this reflection because it
is a high to low η interface.
3r (in phase with 2t) will combine and interfere with 2r ( 3r + 2r = resultant, constructive + or destructive - depends
on the λ). Since 2r has already shifted relative to 2t by 1/2 λ, for + interference to occur, 3r must be shifted in
phase by 1/2 λ , 1 1/2 λ , 2 1/2 λ, etc. For - interference to occur, 3r must be shifted in phase by 0 λ , 1 λ , 2 λ,
etc.
So to solve this for maximum constructive reflective interference, we take:
OPL (2t + 3r) must equal 1/2 λ or 1 1/2 λ or 2 1/2 λ
OPL (2t + 3r) = 2(thickness of polymer x η polymer)
so.... 1/2 λ or 1 1/2 λ or 2 1/2 λ = 2(thickness of polymer x η polymer)
So to solve for this in maximum destructive reflective interference, we take:
OPL (2t + 3r) must equal 0 λ or 1 λ or 2 λ
OPL (2t + 3r) = 2(thickness of polymer x η polymer)
so.... 0 λ or 1 λ or 2 λ or 3λ = 2(thickness of polymer x η polymer)
Now try one in transmission:
2t is split into 3t and 3r; at this point, all these rays are in phase (no shift high to low η). 3r reflects back as 4 within
polymer, its phase then changes relative to 2t.
3t + 4 = resultant, constructive + or destructive - depends on the λ.
So to solve this for max. constructive transmitted interference, we take:
OPL (3r + 4) must equal 0 λ or 1 λ or 2 λ
OPL (3r + 4) = 2(thickness of polymer x η polymer)
so.... 0 λ or 1 λ or 2 λ or 3 λ = 2(thickness of polymer x η polymer)
These integer values (1, 2, 3, etc.) for wavelengths are called 'orders' . As we can see, we lose energy with each
reflection so that the most important orders (with regard to amplitude) are usually the lowest order effects.
single semi-silvered surfaces reflect 50%
and transmit 50% of light (all λ )
η - hi
η - air
η - hi
This diagram may help you solve the extra
credit question on the midterm exam.
for phase shifts on reflection: low to high,
shift in π
high to low, no shift in π
air = white glass = blue light rays = black semi-silvered surfaces = grey
waves/rays = orange
resultant
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
They won’t let you use their calculator for normal (90 degree) incidence so to
try their calculator use a 30 degree angle (answers are close to those for 90).
WOW!
Murphy 2001
out of phase by π,3π ,5π ,
etc.
resources.yesican-science.ca
www.jasondoucette.com/ graphics/interfrs.gif
Note that energy is neither destroyed nor created during
interference.
Laser design inc.
Phase change of 180 deg (pi) when reflection is rare (low
refractive index) to dense (high refractive index), no phase
change when reflection is dense to rare as in TIR or total internal
reflection.
Oil on
water
AR
coating
Georgia State U.
http://hyperphysics.phy-astr.gsu.edu/hbase/hph.html