Download Definition of a Vector Space A collection of vectors: V , scalars for

Definition of a Vector Space
A collection of vectors: V , scalars for scaling : R;
A vector addition: +, A scalar multiplication: ·
for vector addition:
(i) (closure of vector addition) u + v is always in V .
(ii) (commutative law) u + v = v + u.
(iii) (associative law) (u + v) + w = u + (v + w).
(iv) (existence of zero vector) has 0 s.t. u + 0 = u.
(v) (existence of negative vector) for each u ∈ V , there is a
vector −u s.t. u + (−u) = 0.
1
...continued for scalar multiplication:
(vi) (closure of scalar multiplication) cu is always in V .
(vii) (distributive law) c(u + v) = cu + cv.
(viii) (distributive law) (c + d)u = cu + du.
(ix) (compatibility) c(du) = (cd)u.
(x) (normalization) 1u = u.
Def: A non-empty set of vectors V with vector addition
“+” and scalar multiplication “·” satisfying all the above
properties is called a vector space over R.
2
Facts: (i) The zero vector 0 so defined is unique.
0=0+w =w
(ii) The negative vector for each u is unique.
−u = −u + 0 = −u + (u + w)
= (−u + u) + w = 0 + w = w
We define vector subtraction u − v := u + (−v).
(iii) c0 = 0.
(iv) 0u = 0.
(v) −u = (−1)u.
3
Examples of Common Vector Spaces
• {0}, zero vector space.
• Rn : ordered n-tuples of real numbers with entry-wise
vector addition and scalar multiplication.


u1 + v1
..

u+v =
,
.
un + vn
Blue-print for vector space.
4


cu1
.
cu =  .. 
cun
• S, the doubly infinite sequences of numbers:
{yk } = (. . . , y−2 , y−1 , y0 , y1 , y2 , . . .)
with component-wise addition and scalar multiplication.
{yk } + {zk } = (. . . , y−2 , y−1 , y0 , y1 , y2 , . . .)
+ (. . . , z−2 , z−1 , z0 , z1 , z2 , . . .)
:= (. . . , y−1 + z−1 , y0 + z0 , y1 + z1 , . . .)
c{yk } := (. . . , cy−2 , cy−1 , cy0 , cy1 , cy2 , . . .)
zero vector: {0}, sequence of zeros.
5
• Pn : collection of polynomials with degree at most equal
to n and coefficients chosen from R:
p(t) = p0 + p1 t + . . . + pn tn ,
with polynomial operations.
→ “vector addition”: “p(t) + q(t)” is defined as:
p(t) + q(t) = (p0 + q0 ) + (p1 + q1 )t + . . . + (pn + qn )tn ;
→ “scalar multiplication”: “cp(t)” is defined as:
cp(t) = (cp0 ) + (cp1 )t + . . . + (cpn )tn .
→ “zero vector”: the zero polynomial 0(t) ≡ 0.
• P: all polynomials.
6
• The collection of all real-valued functions on a set D, i.e.
f : D → R. (D usually is an interval.)
→ “vector addition”: the function “f + g” is defined as:
(f + g)(x) = f (x) + g(x) for all x in D.
→ “scalar multiplication”: the function “cf ” is defined
as:
(cf )(x) = cf (x) for all x in D.
→ “zero vector”: the zero function 0(x) which sends
every x in D to 0, i.e.
0(x) = 0 for all x in D.
7
• Mm×n : collection of all m × n matrices with entries in
R with matrix addition and scalar multiplication.
(
)
A + B = aij + bij ,
(
cA = caij .
zero vector: m × n zero matrix Om×n .
. . . and many more.
8
)
Subspace: A subspace H of V is a non-empty subset of V
such that H itself forms a vector space under the same vector
addition and scalar multiplication induced from V .
Checking: Following conditions are automatically valid:
(ii) u + v = v + u.
(iii) (u + v) + w = u + (v + w).
(vi) c(u + v) = cu + cv.
(viii) (a + b)u = au + bu.
(ix) (ab)u = a(bu).
(x) 1u = u.
9
Need to verify the remainings:
(i) the sum u + v is always in H.
(iv) there is a zero vector 0 in H.
(v) for each u ∈ H, there is a negative vector −u ∈ H.
(vi) the scalar multiple cu is always in H.
[Same zero vector, negative vector for H.]
.... but we know ...
• −u = (−1)u for any u.
10
Alternative Definition: H is a subspace of V if:
1. 0 of V is in H.
2. sum of two vectors in H is again in H.
3. the scalar multiple of a vector in H is again in H.
In fact, (2) & (3) can be combined together as a single checking condition:
Thm: H is a subspace of V iff H contains 0 and:
u, v ∈ H
⇒
au + bv ∈ H
11
for all scalars a, b.
Examples of Subspaces
1. V is a subspace of itself.
2. {0} is a subspace of V , called the zero subspace.
3. R2 is not a subspace of R3 , strictly speaking.
3′ . The following subset of R3 is a subspace of R3 :
 

 s

H =  t  : s, t in R


0
4. Pn is a subspace of P;
Pn is a subspace of Pm if n ≤ m.
12
5. The collection of n × n symmetric matrices H is a subspace of Mn×n .
5′ . The collection of n × n skew-symmetric matrices is also
a subspace of Mn×n .
6. The collection Ve of even functions from R to R:
f (−x) = f (x) for all x ∈ R
and the collection Vo of odd functions:
f (−x) = −f (x)
for all x ∈ R
are both subspaces of the vector space of functions.
13
Linear Combination and Span
Similar to vectors in Rn , we define:
Def: Let S = {v1 , . . . , vk } be a collection of vectors in V
and let c1 , . . . , ck be scalars. The following y is called a
linear combination (l.c.) of vectors in S:
y = c1 v1 + . . . + ck vk .
Note: When S contains infinitely many vectors, a l.c. of
vectors in S means a l.c. of a finite subset of vectors in S.
Rmk: Sum of infinite number of vectors is not defined (yet).
[We need a concept of “limit” to do this.]
14
Example: In function space, let S = {sin2 x, cos2 x}. Then
the constant function 1(x) ≡ 1 is a l.c. of “vectors” in S:
1(x) = 1 · sin2 x + 1 · cos2 x,
for all x in D.
Example: In polynomial space, let S = {1, t, t2 , t3 , . . .}.
Then any polynomial p(t) is a l.c. of “vectors” in S.
p1 (t) = 1 + t + t3 , S1 = {1, t, t3 }
p2 (t) = 3t − 5t100 , S2 = {t, t100 }
p3 (t) = 0, S3 = {1}
15
Exercise: Consider the function space.
Is sin3 x a l.c. of S = {sin x, sin 2x, sin 3x}?
Exercise: Consider the function space.
Is cos x a l.c. of S = {sin x, sin 2x, sin 3x}?
***
16
Span of a Collection of Vectors
Def: Let S = {v1 , . . . , vk }. The collection of all possible l.c.
of vectors in S is called the span of S:
Span S := {c1 v1 + . . . + ck vk | c1 , . . . , ck are scalars.}.
Note: When S contains infinitely many vectors, Span S is
the collection of all possible l.c. of any finite subset of vectors
in S.
Example: In P, consider S = {1, t2 , t4 , . . .}. Then
Span S = collection of polynomials with only even powers.
17
Thm: Let v1 , v2 be vectors in V . Then H = Span {v1 , v2 }
is a subspace of V .
Checking: (1): 0 = 0v1 + 0v2 , so 0 ∈ H.
(2): Let u, v ∈ H, i.e. both are l.c. of {v1 , v2 }:
u = s1 v1 + s2 v2 ,
v = t1 v1 + t2 v2 ,
for some suitable numbers s1 , s2 , t1 , t2 . Then:
u + v = (s1 + t1 )v1 + (s2 + t2 )v2
is again a l.c. of {v1 , v2 }, and thus collected by H.
18
(3): Let u ∈ H, c a number. Then:
cu = (cs1 )v1 + (cs2 )v2
is a l.c. of {v1 , v2 }, and hence collected by H.
As conditions (1),(2),(3) are all valid, H is a subspace of V .
The above proof allows obvious generalization to:
Thm 1 (P.210): For any v1 , . . . , vp ∈ V , the collection of
vectors H = Span {v1 , . . . , vp } is a subspace of V .
Note: We will call H to be the subspace spanned (or generated) by {v1 , . . . , vp }, and {v1 , . . . , vp } is called a spanning
set (or generating set) of H.
19
Subspaces of a Matrix
Let A be an m × n matrix. Associated to this matrix A,
we define:
1. The null space of A, denoted by Nul A;
2. The column space of A, denoted by Col A;
3. The row space of A, denoted by Row A.
Note that:
• Nul A and Row A will be subspaces of Rn ;
• Col A will be a subspace of Rm .
20
The Null Space of a Matrix
Def: Let A be an m × n matrix. The null space of A is:
Nul A := {x | x in Rn and Ax = 0}.
i.e. the solution set of the homogeneous system Ax = 0.
• size of each solution: no. of columns in A.
so if A is of size m × n, Nul A is inside Rn .
Example: Does v belong to Nul A?
[
1 1
A=
0 −3
]
−1
,
2
21
 
1
v = 2
3
Thm 2 (P.215): Nul A is a subspace of Rn .
Checking: (1) A0 = 0, so 0 is in Nul A.
(2) Let Au = 0 = Av. Then consider u + v:
A(u + v) = Au + Av = 0 + 0 = 0,
so u + v ∈ Nul A.
(3) Let Au = 0, c any number. Then consider cu:
A(cu) = c(Au) = c0 = 0,
so cu ∈ Nul A.
22
Exercise: Describe the null space of A:


1 2 2 1
A =  2 5 10 3  .
1 3 8 2
***
From the above exercise, obviously we will have:
Thm: Nul A = {0} when Ax = 0 has unique solution. When
Ax = 0 has {x1 , . . . , xk } as a set of basic solutions, we have
Nul A = Span{x1 , . . . , xk }.
23
The Column Space of a Matrix
Def: Let A = [ a1 . . .
column space of A is:
an ] be an m × n matrix. Then the
Col A := Span {a1 , . . . , an }.
Fact: Col A is a subspace of Rm .
Exercises: Check if v ∈ Col A:


 
1 2 1 2
1
A =  2 4 0 6  (i) v =  2 
1 2 2 1
1
***
24
 
1
(ii) v =  4  .
7
Thm: v ∈ Col A ⇔ [ A | v ] is consistent.
Example: Find a condition

1
2
 −1 −1
A=
3
2
4
0
Sol: Consider the

1
2
5
 −1 −1 −3

3
2
7
4
0
4
on v such that v ∈ Col A.:

 
5
y1
−3 
 y2 
 v =  .
7
y3
4
y4
augmented matrix [ A | v ]:



| y1
1 2
5
|
y1
| y2 
2
| y2 + y1 
0 1
→



| y3
0 −4 −8 | y3 − 3y1
| y4
0 −8 −16 | y4 − 4y1
25

1
 −1

3
4


2
5 | y1
1 2 5
−1 −3 | y2 
0 1 2
→
2
7 | y3
0 0 0
0
4 | y4
0 0 0

|
y1
|
y1 + y2


| y1 + 4y2 + y3
| 4y1 + 8y2 + y4
For the system to be consistent, we need:
{
y1 + 4y2 + y3 = 0
4y1 + 8y2 + y4 = 0
26
Remark: When A is representing a matrix transformation
T : Rn → Rm , we have:
v ∈ range of T
↔
can find x ∈ Rn such that T (x) = v
↔
[ A | v ] is consistent.
Therefore, Col A is the same as the range of T in this case,
as:
Range of T := {v ∈ Rm | T (x) = v for some x ∈ Rn }.
Thm: Col A = Rm iff every row of A has a pivot position.
(i.e. T : x 7→ Ax is onto.)
27
The Row Space of a Matrix
Identify:
Row ↔ Column by taking transpose


r1
.
Def: Let A =  ..  be an m × n matrix. The row space of
rm
A is:
Row A := Span{rT1 , . . . , rTm }.
i.e. Row A = Col AT .
Note: Row A is a subspace of Rn .
28
Let A → B by an ERO, e.g.




r1
−3r2 + r1
r2
=
A =  r2  → 
..
..
.
.

r′1
 r′2

..
.


 = B.
Then r′1 , r′2 , . . . ∈ Row A. So:
T
T
Row B ⊆ Row A.
But B → A by the reverse ERO, then we also have:
Row A ⊆ Row B.
29
Thm: Let A → B by EROs. Then Row A = Row B.
Recall: A → B = P A where P (size: m × m) is invertible.
Thm: When P is invertible, Row A = Row (P A).
[
]
1 1 3
Example: Describe Row A when A =
.
2 2 4
Sol: By definition:
   
1
2
Row A = Span { 1  ,  2 }.
3
4
30
[
1
Example: Describe Row A when A =
2
1
2
3
.
4
Sol: By EROs:
[
1 1
A=
2 2
]
[
]
3
1 1 0
→
= B.
4
0 0 1
As Row A = Row B, we have:
   
1
0
Row A = Span { 1  ,  0 }.
0
1
31
]
Linear Transformations in general
Def: Let V , W be two vector spaces over R. A transformation T : V → W is called linear if
(a) T (u + v) = T (u) + T (v)
(b) T (cu) = cT (u)
for any choices of u, v in V and any choice of scalar c.
In the special case that V = W , i.e. T : V → V is linear, we
will call T to be a linear operator on V .
32
Def: Let T : V → W be linear. We define:
1. The kernel of T , denoted by ker T , to be:
ker T := {v ∈ V : T (v) = 0} .
(solution set of T (v) = 0.)
2. The image/range of T , denoted by Im T , to be:
Im T := {w ∈ W : T (v) = w for some v ∈ V } .
(which is the same as T (V ).)
Thm: ker T is a subspace of V . Im T is a subspace of W .
33
Remark: When V = Rn , W = Rm , i.e. T is given by a
matrix transformation: x 7→ Ax. Then:
ker T = Nul A and Im T = Col A.
Thm: T is one-to-one iff ker T = {0}.
T is onto iff Im T = W .
Pf: (1-1) As T is linear, we have:
T (x1 ) = T (x2 ) ⇔ T (x1 − x2 ) = 0.
So T is one-to-one ⇔ always have x1 = x2 ⇔ ker T = {0}.
For onto property, directly from definition.
34
Example: Consider V = W = P(R). The differential operator D will be a linear transformation:
d
D(p(t)) = p(t).
dt
We have ker D = Span {1} and Im D = P.
• Thus D is onto but NOT one-to-one.
Example: The integral operator Ia : P → P with lower
limit a:
∫ t
p(x)dx.
Ia (p(t)) =
a
will be one-to-one but NOT onto.
35
Linearly Independent/Dependent Sets
Def: An indexed set of vectors S = {v1 , . . . , vp } is called
linearly independent (l.i.) if the vector equation:
c1 v1 + . . . + cp vp = 0
has unique (zero) solution:
c1 = . . . = cp = 0.
Def: S is called linearly dependent (l.d.) if it is not l.i., i.e.
exist d1 , . . . , dp , not all zeros, such that:
d1 v1 + . . . + dp vp = 0.
36
Note: When S contains infinitely many vectors:
(i) S is said to be l.i. if every finite subset of S is always l.i.
(ii) S is said to be l.d. if there exists a finite subset of S
being l.d.
Example: In P2 (R), S = {1, 2t, t2 } is l.i.
Sol: Consider the “vector” equation:
c1 · 1 + c2 · 2t + c3 · t2 = 0(t) (as polynomials).
By equating coefficients of 1, t, t2 , we get c1 = c2 = c3 = 0.
Rmk: The above equation is a polynomial “identity”.
37
Example: In P2 , S = {1 + t, 1 − t2 , t + t2 } is l.d. since:
c1 (1 + t) + c2 (1 − t2 ) + c3 (t + t2 ) = 0(t)
has a non-zero solution (c1 , c2 , c3 ) = (1, −1, −1).
Example: In P, S = {1, t, t2 , t3 , . . .} is l.i.
Sol: Take any finite subset of S:
S ′ = {ti1 , ti2 , . . . , tik },
0 ≤ i1 < i2 < . . . < ik .
Obviously S ′ is always l.i., so S will be l.i.
38
Example: In function space, S = {sin2 x, cos2 x} l.i.
Sol: Consider the “vector” equation:
c1 sin2 x + c2 cos2 x = 0(x) (as functions).
Put x = 0, π2 , we obtain “number” equations:
{
c1 · 0 + c2 · 1 = 0
c1 · 1 + c2 · 0 = 0
from which we get c1 = c2 = 0 already. So S must be l.i.
39
Example: In function space, S = {1, sin2 x, cos2 x} is l.d.
Sol: We have non-trivial solution to the “vector” equation:
(−1) · 1 + (1) · sin2 x + (1) · cos2 x = 0(x),
which is true for all x ∈ D.
Exercise: Let c1 , c2 , c3 be distinct numbers. In function
space, is {ec1 x , ec2 x , ec3 x } l.i.?
***
40
Bases, Coordinates, and Dimensions
• When {v1 , . . . , vp } is l.d., we can remove one vj from
the set without changing its span.
e.g. Consider {v1 , v2 , v3 } with v2 = 3v1 − 4v3 .
the l.c. x = a1 v1 + a2 v2 + a3 v3 can be rewritten as:
x = a1 v1 + a2 (3v1 − 4v3 ) + a3 v3
= (a1 + 3a2 )v1 + (a3 − 4a2 )v3 .
which is a vector in Span {v1 , v3 }.
• If removing any vector from {v1 , . . . , vp } will change its
span, the set must be l.i.
41
Basis for a Subspace
Def: Let H be a subspace of V . An indexed set B of vectors
in H is called a basis for H if:
(i) B is linearly independent; and
(ii) Span B = H.
When H = {0}, we choose B = ϕ as the basis.
Remarks: (i) Since Span B = H, every vector in H can be
written as a l.c. of vectors in B.
(ii) Since B is l.i., removing any vector from it will make
the span smaller. So we can regard a basis as a “minimal
collection of vectors” from H that can span H.
42
Examples: (i) {e1 , . . . , en } is a basis for Rn .
[ ] [ ]
[
] [ ]
1
0
1
1
(ii) Both {
,
} and {
,
} are bases for R2 .
0
1
−1
1
(iii) {1, t, t2 , . . . , tn } forms a basis for Pn .
P has a basis {1, t, t2 , . . .}.
(iv) The following set of matrices is a basis for the vector
space of 2 × 2 matrices.
[
] [
] [
1 0
0 1
0
B={
,
,
0 0
0 0
1
43
] [
]
0
0 0
,
}.
0
0 1
(v) Check that B is a basis for R3 .

 
 

3
−4
−2
B = { 0  ,  1  ,  1 }.
−6
7
5
Sol: Consider the equation:






3
−4
−2
c1  0  + c2  1  + c3  1  = b.
−6
7
5
44





3 −4 −2
c1
b1
↔ 0
1
1   c2  =  b2  .
−6 7
5
c3
b3
We find that the coefficient matrix is invertible. So:
• B is linearly independent.
(all basic variables, unique solution for c1 , c2 , c3 .)
• Span B = Col A = R3 .
(every row of A has a pivot position.)
Thus, B is a basis of R3 .
Thm: Let [ a1 . . . an ] be an n×n invertible matrix. Then
B = {a1 , . . . , an } will form a basis for Rn .
45
Bases for Nul A
Express the general solution of Ax = 0 in parametric form:
x = s1 x1 + . . . + sk xk ,
where s1 , . . . , sk ∈ R.
So B = {x1 , . . . , xk } can span Nul A.
We note that B must be l.i., for example:






−s − t
−1
−1
x =  s  = s 1  + t 0 .
t
0
1
x = 0 iff s = t = 0.
46
Thm: When Ax = 0 has non-zero solutions, a set of basic
solutions B = {x1 , . . . , xk } will form a basis for Nul A.
When Ax = 0 has unique zero solution, i.e. Nul A = {0}, we
say that ϕ is the basis for Nul A.
Exercises: Find a basis for Nul A where:

[
]
1 1 2 2
1 2
(i) A =
, (ii) A =  2 2 1 1
2 1
3 3 2 2
***
47

3
3.
2
Bases for Row A
Recall when A → B by EROs, we have Row A = Row B. So
let B be a REF of A. Clearly the non-zero rows of B will
span Row B = Row A, and also they form a l.i. set, e.g.:
     

1
0
0
1 1 1 1
1 2 0
0 2 3 4
B=
 ↔ B = {  ,   ,  }
0 0 0 5
1
3
0
0 0 0 0
1
4
5
 
   
 
1
0
0
0
1
2
0 0
c1   + c2   + c3   =   ,
1
3
0
0
1
4
5
0

48
unique solution: c1 = c2 = c3 = 0.
Thm 13 (P.247): Let B be a REF of A. Then the non-zero
rows of B will form a basis for Row A.
Exercise: Find a basis for Row A:

1
1
A=
2
1
4
1
5
0
***
49

6 8
3 2 
.
9 10
2 0
Bases for Col A
We use the trick: Col A = Row AT .
Example: Find a basis for

1
2
A=
1
1
Sol: Perform EROs

1
2
T
A =
1
1
on
2
3
1
2
AT :
1
3
1
3
Col A:
2
3
3
2
1
1
1
1
1
2
.
3
1


1
1
2
0
→
1
0
1
0
50

2
1
0
0
1
0
1
0

1
0

0
0
A basis for Col A will be:
     
1
0
0
2 1 0
B = {  ,   ,  }.
1
0
1
1
0
0
Warning: Row operations on A will change Col A!.
• i.e. EROs needed to be performed on AT .
(then Row AT = Col A will not change.)
51
If we want to use only the columns from A to form such a
basis, we have the following result:
Thm 6 (P.228): The pivot columns of A will form a basis
for Col A.
Exercise: Find a basis for Col A, using columns from A:

1
2
A=
1
1
2
3
3
2
***
52
1
1
1
1

1
2
.
3
1
Idea of Proof of Thm 6:
1. A l.c. of columns of A:
c1 a1 + . . . + cn an = b
corresponds to a solution of Ax = b: xi = ci
2. Row operations [ A | b ] → [ A′ | b′ ] will not change this
solution, i.e. same dependence relation for new columns:
c1 a′1 + . . . + cn a′n = b′
3. In RREF(A) the pivot columns are automatically l.i.,
spanning Col RREF(A). These two properties can be
brought back to pivot columns in A by reverse EROs.
53
Recall: Studying V using a basis B
Basis: An indexed set B of vectors that is:
(a) linearly independent;
(b) spanning the space V , i.e. Span B = V .
Thm 7 (P.232): Let B = {b1 , . . . , bp } be a basis for a subspace H (or V ). Then for each x ∈ H, there exists a unique
set of scalars (c1 , . . . , cp ) such that:
x = c1 b1 + . . . + cp bp .
54
Proof: The existence of {c1 , . . . , cp } is guaranteed by condition (b). Now suppose that d1 , . . . , dp are numbers with the
same properties, i.e.
x = d1 b1 + . . . + dp bp .
Take the difference, then:
0 = (c1 − d1 )b1 + . . . + (cp − dp )bp .
As B is l.i. (condition (a)), ci − di = 0 for each i.
Hence the numbers c1 , . . . , cp are uniquely determined.
55
Coordinate Vector Relative to a Basis
Def: Let B = {b1 , . . . , bp } be a basis for H. The coordinate
vector of x relative to B (or B-coordinate vector of x) is the
vector in Rp formed by the numbers c1 , . . . , cp :

c1
.. 

[x]B := . .
cp

x = c1 b1 + . . . + cp bp
↔
Note that x is in H ⊂ V , but [x]B is in Rp .
56
[
] [
]
2
−2
Example: Let B = {
,
} be a basis for R2 . De−1
−1
[ ]
x1
scribe geometrically the B-coordinate vector of x =
.
x2
Sol: First we find [x]B :
[
x1
x2
]
[
= c1
]
[
2
−2
+ c2
−1
−1
]
↔

x1 − 2x2

 c1 =
4

 c2 = − x1 + 2x2
4
So the B-coordinate vector of x is:
[ ] [ x1 −2x2 ]
c1
4
[x]B =
=
x1 +2x2 .
c2
− 4
57
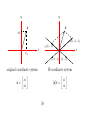
y
y
x
x
x2
c2 (−2,−1)
x1
c1 (2,−1)
x
(−2,−1)
x
(2,−1)
B-coordinate system
[ ]
c1
[x]B =
c2
original coordinate system
[ ]
x1
x=
x2
58
Example: Let B = {1, 1 + t, 1 + t + t2 } be a basis for P2 .
Consider p(t) = t − t2 . To find the B-coordinate vector of
p(t), we express p(t) as a l.c. of vectors in B:
t − t2 = (−1) + 2(1 + t) − (1 + t + t2 ).
Then the B-coordinate vector of p is:


−1
[p]B =  2  .
−1
59
Example: Let H = Span B where B = {1, cos x, cos 2x}.
It is easy to check that B is l.i., so it is a basis for H.
Let f (x) = cos2 x. Since f (x) = 12 +
1
1
2
cos 2x, we have:
2
[f ]B =  0  .
1
2
But if we take B ′ = {cos x, 1, cos 2x}, we have:
 
0
[f ]B′ =  21  .
1
2
So the ordering of vectors in a basis is important.
60

 
 

1
1
−1
Exercise: Let B = { 1  ,  −1  ,  1 } be a basis for
−1
1
1
R3 . Find [e1 ]B , [e2 ]B , and [e3 ]B .
***
Def: The mapping x 7→ [x]B is called the coordinate mapping determined by B, or simply B-coordinate mapping.
Thm
Then
linear
linear
8 (P.235): Let B = {b1 , . . . , bp } be a basis for H.
the B-coordinate mapping is a one-to-one and onto
transformation from H to Rp . Its inverse is also a
transformation from Rp back to H.
Proof: Direct verification.
61
Under this coordinate mapping, any linear problem in V can
be translated to a corresponding problem in Rp , and then
we are equipped with the powerful matrix theory.
Example: Check that the set of vectors:
{t + t3 , 1 − t + t2 , 5 − 3t3 , 4 + 2t2 , 3 − t + t3 },
is l.d. in P3 .
Can check it directly by solving the polynomial identity.
Sol: Let B = {1, t, t2 , t3 }. By B-coordinate mapping, they
are sent to:
62
  
 
   

0
1
5
4
3




1
−1
0
0
−1
  
 
   

,
,
,
,
  
 
   

0
1
0
2
0




1
0
−3
0
1
5 vectors in R4 must be l.d., i.e. exists c1 , . . . , c5 , not all
zeros, such that:

  

 



 
0
3
4
5
1
0
 −1   0 
0
 0 
 −1 
1
c1   + c2 
 =  .
 + c4   + c5 
 + c3 
0
0
2
0
1
0
0
1
0
−3
0
1
63
Under inverse B-coordinate mapping, we obtain a dependence relation among the 5 polynomials in P3 :
c1 (t + t3 ) + c2 (1 − t + t2 ) + c3 (5 − 3t3 )
+ c4 (4 + 2t2 ) + c5 (3 − t + t3 ) = 0(t).
So the 5 polynomials are l.d. in P3 .
The technique used above generalizes to:
Thm 9 (P.241): Let B = {b1 , . . . , bp } be a basis for H.
Then any subset in H containing q > p vectors must be l.d.
Proof: Send these q vectors by B-coordinate mapping to q
vectors in Rp .
64
Thm 10 (P.242): Let B and C be two bases for V consisting
of n vectors and m vectors respectively. Then n = m.
Pf: First consider B as a basis for V .
• If m > n, C must be l.d. by previous theorem.
• Since C is l.i., we must have m ≤ n.
Now consider C as a basis for V .
• If n > m, B must be l.d. by previous theorem.
• Since B is l.i., we must have n ≤ m.
Therefore n = m.
65
Dimension of a Vector Space
Def: When V has a basis B of n vectors, V will be called
finite dimensional of dimension n or n-dimensional. We will
write dim V = n.
Def: The dimension of the zero space {0} is defined to be 0.
Def: If V cannot be spanned by any finite set of vectors, V
will be called infinite dimensional. We will write dim V = ∞.
Examples: dim Rn = n, dim Pn = n + 1, dim P = ∞.
Basis for Rn : E = {e1 , . . . , en }
Basis for Pn : {1, t, t2 , . . . , tn }
Basis for P: {1, t, t2 , . . .}
66
Let H be a subspace of V and dim V = n ≥ 1.
Thm 11 (P.243): Any l.i. set in V can be extended to a
basis for V . In particular, if H is a subspace of V , we have:
dim H ≤ dim V,
and if dim H = dim V , we have H = V .
Proof: Let S be a l.i. set in V .
1. If Span S = V , S is already a basis.
2. If not, there will be a vector u ∈
/ Span S.
3. The set S ∪ {u} will have one more element, still l.i.
67
(For the equation c1 v1 + . . . + cp vp + cp+1 u = 0; first
show cp+1 = 0 using (2), then show c1 = . . . = cp = 0.)
4. Go back to (1) with new S ′ = S ∪ {u}.
Such addition of vectors must stop somewhere since l.i.
set in V cannot contain more than n vectors.
(Process stops → the l.i. set S ′ can span V .)
If dim H = dim V , first choose any basis B for H.
a. dim H = |B| = n(= dim V ) by assumption.
b. Extend B to B′ , a basis for V , by adding suitable vectors.
c. Any l.i. set in V cannot contain more than n vectors.
d. Must have B ′ = B (adding no vector in (b)), and hence
H = Span B = Span B ′ = V .
68
The proof of previous theorem says that:
Thm 12 (P.243): Let dim V = n ≥ 1. Then
(a) Any l.i. set with n vectors is a basis for V .
(b) Any spanning set of V with n vectors is a basis for V .
Proof: (a) We cannot add vector to S as before since any
set with n + 1 vectors must be l.d., so S is a basis for V .
(b) If S is l.d., we can remove certain vector in S and obtain
a smaller set S ′ which still spans V . Keep removing vectors
until S ′ is l.i., and thus forming a basis for V . This S ′ contains dim V = n vectors, i.e. we actually remove nothing
from S.
69
So, any two of the conditions will characterize a basis S:
(a) |S| = n = dim V .
(b) S is l.i.
(c) S spans V .
0. (b) & (c): (original defintion)
1. (a) & (b): Any l.i. set of n = dim V vectors is a basis.
2. (a) & (c): Any spanning set of n = dim V vectors is a
basis.
70
Example: Describe all possible subspaces of R3 .
Sol: Let H be a subspace of R3 . Then dim H = 0, 1, 2, 3.
0. dim H = 0. H = {0} is the only possibility.
3. dim H = 3. Then H = R3 .
1. dim H = 1. Then H has a basis B = {v}.
→ every x ∈ H is a l.c. of {v};
i.e. x = cv where c ∈ R.
→ H is a line passing through origin, containing v.
2. dim H = 2. Then H has a basis B = {v1 , v2 }.
→ every x ∈ H is of the form x = c1 v1 + c2 v2 .
→ H is a plane through 0, containing both v1 , v2 .
71
Dimensions of Nul A, Row A, and Col A
Def: The dimension of Nul A is called the nullity of A.
Def: The dimension of Row A is called the row rank of A.
Def: The dimension of Col A is called the column rank of A.
Let A be an m × n matrix with p pivot positions. Then
A has n − p free variables, and so the general solution of
Ax = 0 can be written as:
x = s1 x1 + . . . + sn−p xn−p ,
where s1 , . . . , sn−p ∈ R.
Thm: nullity of A = dim Nul A = n − p.
72
Let A be an m × n matrix with p pivot positions. Then
there are p non-zero rows in a REF of A.
Thm: row rank of A = dim Row A = p.
Let A be an m × n matrix with p pivot positions. Then
there are p pivot columns of A:
Thm: column rank of A = dim Col A = p.
Recall the definition that rank A = no. of pivot positions
in A. So:
Thm: row rank of A = column rank of A = rank A.
73
In summary, we have the following “rank theorem”:
Thm 14 (P.249): Let A be an m × n matrix. Then:
dim Row A = dim Col A = rank A
rank A + dim Nul A = n.
In the language of matrix transformations, we have:
Thm: Let T : Rn → Rm be a matrix transformation. Then:
dim Im T + dim ker T = n = dim Rn .
74