Download (SSS) Congruence: If three sides of one triangle are congruent to

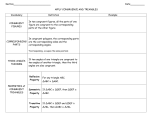
Postulate - Side-Side-Side (SSS) Congruence: If three sides of one triangle are congruent to
three sides of a second triangle, then the triangles are congruent.
Picture:
Postulate - Side-Angle-Side (SAS) Congruence: If two sides and the included angle of one
triangle are congruent to two sides and the included angle of a second triangle, then the
triangles are congruent.
Picture:
Postulate – Angle-Side-Angle (ASA) Congruence: If two angles and the included side of one
triangle are congruent to two angles and the included sided of another triangle, then the triangles
are congruent.
Picture:
Postulate – Angle-Angle-Side (AAS) Congruence: If two angles and the non-included side of
one triangle are congruent to two angles and the non-included sided of another triangle, then the
triangles are congruent.
Picture:
Postulate – Hypotenuse-Leg (HL) Congruence: If the hypotenuse and a leg of one right
triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are
congruent.
Picture:
Corresponding Parts of Congruent Triangles Are Congruent!!
*Must be used AFTER you have two congruent triangles
Triangle Angle Sum: The sum of the three angles of any triangle equals 180o.
Exterior Angle: The measure of an exterior angle of a triangle is equal to the sum of the measures of the two
remote interior angles.
Angle Bisector: An angle bisector divides an angle into two congruent parts.
*Creates congruent angles
**Halves of equal angles are equal
Segment Bisector:
A segment bisector creates a midpoint.
*Creates a midpoint and congruent segments
Midpoint:
A midpoint divides a segment into two congruent parts.
*Creates congruent segments
Vertical Angles:
Vertical angles are congruent.
*Creates congruent angles
Reflexive Property:
Anything equals itself.
*Creates a “shared piece” step
Perpendicular Lines: (┴)
Perpendicular lines form right angles.
*Creates 2 steps in a proof: FIRST it creates 90o angles, SECOND it creates congruent angles.
Right Angles:
ALL right angles are congruent.
o
*Creates 90 congruent angles
Parallel Lines: (║)
Parallel lines never intersect.
*Creates either congruent angles (corresponding, alternate interior, alternate exterior) or
supplementary angles (consecutive interior)
Complementary Angles:
Two angles whose sum is 90o.
*Complements of congruent angles are congruent
Supplementary Angles:
Two angles whose sum is 180o.
*Supplements of congruent angles are congruent
Distance Formula:
*Proves type of triangle: Scalene, Isosceles, Equilateral
Isosceles Triangle: If two sides of a triangle are congruent, then the angles opposite those sides are congruent.
Converse: If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
Corollaries for the Equilateral Triangle: A triangle is equilateral if and only if it is equiangular.
*An equilateral triangle has angles that each measure _________________.
Geometry
CONGRUENT TRIANGLES
Day 1
Classifying Triangles/Finding the Missing Side
Day 2
Angles of Triangles/Congruent Triangles
Day 3
Corresponding Parts/Postulates/Definitions
Day 4
QUIZ REVIEW
Take Home QUIZ
Day 5
Proving Triangles - SSS, SAS
Day 6
Proving Triangles – ASA, AAS, HL two column proofs
Day 7
CPCTC
Day 8
Overlapping Triangles
Day 11
OPEN NOTE QUIZ
Day 12
Isosceles and Equilateral Triangles
Day 13
Congruence Transformations/Triangles and Coordinate Proofs
Day 14
Review
Day 15
TEST
DAY 1
By Angle:
By Side:
Classifying Triangles
1.
Given:
Isosceles Triangle ABC
AC = CB
AB = 9x - 1
AC = 4x + 1
BC = 5x – 0.5
Find the measures of the sides of ΔABC.
2.
Given:
ΔFGH is equilateral.
Find the measures of the sides of
ΔFGH.
G
2y + 5
3y - 3
F
H
5y – 19
Problem Set:
DAY 2
More information on Triangles
Problem Set:
DAY 3
Corresponding Parts
Problem Set:
(w, x, y, and z)
DAY 4
QUIZ REVIEW
Use a protractor and ruler to classify the triangle as right, acute, obtuse and scalene, isosceles,
equilateral.
If ∆XYZ = ∆ABC, side XY corresponds with side ____________.
Determine whether ∆MNO = ∆QRS and classify each triangle using sides and angles.
M(0, -3) N(1, 4) O(3, 1)
Q(4, -1) R(6, 1) S(9, -1)
In triangle ABC, m<A = 48°, and m<C = 24°. What type of triangle is triangle ABC ?
The angles of a triangle are in the ratio of 1:3:5. Find the measure of the largest angle of the
triangle.
In triangle DEF, m<D = 37° and m<F = 56°. Find the measure of an exterior angle at E.
Day 5
Two Column Proofs
Write a two column proof.
Given:
L
MN = PN
LM = LP
M
Prove:
ΔLMN = ΔLPN
N
P
STATEMENT
REASON
Write a two column proof.
B
Given:
BD ┴ AC
BD bisects AC
Prove:
A
ΔABD = ΔCBD
C
D
STATEMENT
REASON
Problem Set:
DAY 6
Two column proofs
Write a two column proof.
P
Q
Given:
QS bisects <PQR
<PSQ = < RSQ
Prove:
ΔPQS= ΔRQS
S
R
STATEMENT
REASON
Write a two column proof.
R
S
U
Q
STATEMENT
Given:
RQ = ST
RQ ║ ST
Prove:
ΔRUQ = ΔTUS
T
REASON
Write a two column proof:
C
B
P
Q
A
Given: PB ┴ AC, PD ┴ AE, AB = AD
Prove: ΔABP = ΔADP
D
E
STATEMENT
Problem Set:
REASON
DAY 7
Two column proofs
A
B
D
C
Given: BA = DC
<BAC = <DCA
Prove: AD = BC
STATEMENT
REASON
Given: JM = NK
L is the midpoint of JN and KM
J
K
L
Prove: <JMK = <NKM
M
STATEMENT
REASON
N
A
Given: BD bisects <B
BD ┴ AC
D
Prove: <A = <C
C
STATEMENT
B
REASON
A
B
D
C
Given: BA = DC
<BAC = <DCA
Prove: BC = DA
STATEMENT
REASON
Problem Set:
DAY 8
Two column proofs
Q
Given:
Prove:
ΔTPQ= ΔSPR
<TQR = <SRQ
R
P
ΔTQR= ΔSQR
T
STATEMENT
Given:
Prove:
REASON
HL = HM
PM = KL
PG = KJ
GH = JH
<G = <J
STATEMENT
S
G
J
H
P
M
REASON
L
K
Given:
Prove:
<K = <M
KP ┴ PR
MR ┴ PR
K
<KPL = <MRL
P
STATEMENT
M
L
REASON
R
Problem Set:
B
1.
Given:
Prove:
AB = AD
AC bisects <BAD
A
C
ΔABC= ΔADC
D
R
2.
Given:
Prove:
AS ┴ RT
A is the midpoint of RT
A
ΔRAS= ΔTAS
T
S
A
3.
Given:
AR ┴ CB
AR bisects <CAB
Prove:
ΔACR= ΔABR
C
B
R
E
4.
Given:
Prove:
DCFA
<E = <B
ED = AB
FD ┴ DE
CA ┴ AB
EF = CB
D
C
F
A
B
DAY 10
1.
Isosceles/Equilateral Triangles
In isosceles triangle MNP, <P is congruent to <M, side NM is 11 cm, and
<N = 120o. Find the measures of <P and< M, and the length of PN.
1.
Find x and y.
80
4y – 2
2y + 2
6x + 8
Write a two column proof.
B
A
E
STATEMENT
Given:
ΔABC is isosceles
EB bisects <ABC
Prove:
ΔABE = ΔCBE
C
REASON
Problem Set:
DAY 11
CONGRUENCE TRANSFORMATIONS
Reflection:
Translation:
Rotation:
1.
Triangle XZY with vertices X(2, -8), Z(6, -7) and Y(4, -2) is a transformation of ΔABC
with vertices of A(2, 8), B(6, 7), and C(4, 2). Graph the original figure and its image.
Identify the transformation and verify that it is a congruence transformation.
2.
The Bermuda Triangle is a region formed by Miami (Florida), San Jose (Puerto Rico), and
Bermuda. The approximate coordinates of each location, respectively, are 26o N 80o W,
18.5o N 66o W, and 33o N 65o W. Write a coordinate proof to prove that the Bermuda
Triangle is scalene.
3.
Write a coordinate proof to prove that ΔABC is an isosceles triangle if the vertices are
A(0,0), B(a,b), and C(2a, 0).
Problem Set:
9.
10.
11.