Download Newton`s First Law Drawing Force Diagrams Adding Vectors

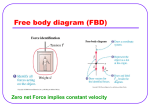
Newton’s First Law
Drawing Force Diagrams
Adding Vectors
Rhine
Newton’s 1st Law (Law of Inertia)
• An object
– at rest tends to stay at rest or...
– in motion tends to stay in motion with a
constant (uniform) speed and direction (i.e.,
constant velocity) (must travel in a straight line)
– unless acted upon by a “net external force”
(“unbalanced force”) (if so, can use Newton’s 2nd
Law!!)
• So if one of the first two statements are
true, the net external force must be zero
Net external force is also known as...
• the TOTAL force acting on an object
• the sum of the forces ( Σ F)
(where Σ is the capital Greek letter “sigma”, which in
math means “the sum of a series of numbers”)
• the net force
• the resultant force
Equilibrium
an object is said to be in “equilibrium”
if Newton’s 1st Law applies (balanced forces)
• Static Equilibrium – not moving
• Dynamic Equilibrium – constant velocity
• For both types of equilibrium, the sum of all the
forces must be equal to zero
– Treat x & y directions independently
– Find ΣFX-Direction and set = 0
– Find ΣFY-Direction and set = 0
• if NOT in equilibrium (unbalanced forces), the
object is...
– NOT at rest
– NOT at a constant velocity
– therefore it must be ... _________________________
Force Diagrams
(also known as “free body diagrams”, FBD)
• Keep them SIMPLE
– Use a circle or box or dot to represent object
• Label each force with a simple, descriptive name (e.g.,
Fgravity or Fg or Ffriction or Ff)
• If you know the value of a force, include it
• Draw to scale, if known (if one force is twice another, use
twice the length)
• After drawing, you will typically ADD all the forces to
apply Newton’s 1st (and 2nd) laws
–
–
–
–
Typically treat x- and y- directions independently
Find ΣFX-Direction and set = 0 if in equilibrium
Find ΣFY-Direction and set = 0 if in equilibrium
Once you do this, you will probably be able to solve for the
unknown force(s)!!
Directions...
• For each of the following scenarios, draw a
simple force diagram (FBD)
• If you need to make any assumptions, state
them! For example: assume all of the situations
occur here on earth!
• Label each force
• Find the sum of all the forces & apply Newton’s
First Law
• Which situations are in static equilibrium?
Dynamic equilibrium? NOT in equilibrium?
1. Apple hanging from tree (motionless)
+y
1. Apple hanging from tree (motionless)
+x
Ftension
Apply Newton’s 1st Law:
+ FTension - Fgravity = ΣF = 0
m = 200 g
Fg = W = mg
= 0.2 kg * 10 m/s2 = 2 N
2. Book sitting on a table
3 lbs
2. Book sitting on a table
Ftable = Fsupport
object is at rest, so
the net external
force, ΣF,
equals...?
3 lbs
Fg = W = mg
= 3 lbs
per Newton’s 1st,
this force must be
equal and
opposite Fg to
zero out total
3. a hockey puck sliding along the ice at a
constant velocity (assume no friction)
m = 200 g
3. a hockey puck sliding along the ice at a
constant velocity (assume no friction)
Fsupport (= 2N per Newton’s 1st)
constant V, so the
net external force,
ΣF, equals...?
velocity
m = 200 g
Fg = W = mg
= 0.2 kg * 10 m/s2 = 2 N
4. a hockey puck sliding along the ice
(assume friction)
m = 200 g
4. a hockey puck sliding along the ice,
slowing down (assume friction)
friction slows puck,
decreasing V, so the
net external force, ΣF,
does NOT equal...?
Ffriction
Fsupport (= 2N per Newton’s 1st)
velocity
m = 200 g
Ffriction always
opposes intended
motion
Fg = W = mg
= 0.2 kg * 10 m/s2 = 2 N
Hint: break the problem
into 2 parts – the up-down
motion (y direction) and
the left-right motion (x
direction). Puck not
moving up-down, so at
rest in that direction (so
ΣFy = 0). Puck constant V
in left-right direction (so
ΣFy = 0).
5. A box sitting on a ramp
20 l
b
5. A box sitting on a ramp
object is at rest, so
the net external
force, ΣF,
equals...?
Fsupport
Ffriction
ΣF = 0
20 l
b
Fg = W = mg
= 20 lb
so Fsupport + F Friction + Fg = 0
Problem: how to add vectors
that are not aligned?
6. A box sliding down a ramp
with a constant velocity
20 l
b
7. A box sliding down a ramp
but slowing down
20 l
b
8. A box sliding down a ramp
but speeding up
20 l
b
9. Abraham (m = 2.5 kg) hanging by one arm from
the top of his cage, with one toe on a scale on the
ground (scale reads 5N)
10. Abraham (m = 2.5 kg) hanging by both arms
from the top of his cage, arms straight up
11. Abraham (m = 2.5 kg) hanging by both arms
from the top of his cage, arms spread out
12. Abraham (m = 2.5 kg) hanging by both arms
from the top of his cage, one arm straight up, one
at an angle
Prove it!
• Rank order the tension in Abraham’s arms
from largest to smallest in scenarios 9-12:
• How can you prove your answer is correct?
13. The apple falls off the tree
m = 200 g
14. You are in the process of kicking a kickball
straight up into the air (foot still on the ball)
m = 1 kg
15. The kickball leaves your foot and travels upward
m = 1 kg
Aside: What happens to the velocity of the ball as it travels upward?
16. The kickball as it reaches its peak height
m = 1 kg
Aside: What is the velocity of the ball at this peak height?
17. The kickball is falling back to the ground
m = 1 kg
Aside: What happens to the of the ball as it travels downward?
18. The kickball is in the process of hitting
the ground
m = 1 kg
Aside: What happens to the of the ball as it travels downward?
19. You are in the process of kicking a ball
at a 30° angle (foot on the ball)
m = 1 kg
20. The ball you kicked at a 30° angle
leaves your foot and flies through the air
m = 1 kg
21. A helium balloon floating up
m = ??
Force diagrams for a 1 kg ball dropping with air resistance:
as ball speeds up, air resistance force increases until...???
Initially, ball is
moving slowly,
so air resistance
is negligible.
Ball accelerates
at 10 m/s per
sec (= 10 m/s2)
(each second,
speed increased
+
by 10 m/s)
As speed
increases, air
resistance
begins to
increase. Net
force still
DOWN
(accelerating
DOWN, but now
accel < 10 m/s2)
Ffriction = 3N
¯
ΣF = –10 N
Fg = 10N
ΣF = +3 –10 = –7 N
Fg = 10N
Speed increases
even more, air
resistance even
greater, and
acceleration
downward even
lower (still gaining
speed, not nearly
as fast)
Speed increases to point
that air resistance force
equals gravitational: now
sum of forces = 0
Ball now in DYNAMIC
EQUILIBRIUM! (at
constant velocity, a.k.a.
“Terminal Velocity”)
Ffriction = 10N
Ffriction = 6N
ΣF = +6 –10 = –4 N
Fg = 10N
ΣF = +10 –10 = 0 N
Fg
= 10N
Questions...
1. Which of the scenarios above use only ONE
dimension?
2. Which of the scenarios are in static
equilibrium?
3. Which of the scenarios are in dynamic
equilibrium?
4. Which of the scenarios are NOT in
equilibrium? (unbalanced)
5. For the non-equilibrium scenarios, what
happens to the object?