* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ELECTRO-OPTIC DIFFRACTION GRATING EMPLOYING
Nonlinear optics wikipedia , lookup
Photon scanning microscopy wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Upconverting nanoparticles wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Smart glass wikipedia , lookup
Reflection high-energy electron diffraction wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Diffraction topography wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
Retroreflector wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Scanning electrochemical microscopy wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
Gaseous detection device wikipedia , lookup
Low-energy electron diffraction wikipedia , lookup
Powder diffraction wikipedia , lookup
ELECTRO-OPTIC DIFFRACTION GRATING EMPLOYING ELECTROPHORESIS, SUPERCAPACITANCE, AND TOTAL INTERNAL REFLECTION by Jason C. Radel B.S., The University of St. Thomas, 2008 M.Sc., The University of British Columbia, 2011 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in THE FACULTY OF GRADUATE AND POSTDOCTORAL STUDIES (Physics) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) May 2015 © Jason C. Radel, 2015 Abstract Light beam steering is required in fields ranging from industrial laser drilling to telecommunications. Current methods for light beam steering to angles greater than 10° rely on mechanically moving parts, which results in expensive and difficult-to-maintain systems. An alternative method for light beam steering is presented that redirects a light beam to an angle of 33° without the need for moving parts. This is achieved by altering the reflectance of a surface by controlling the concentration of dye ions in a region adjacent to an optically transparent and electrically conductive thin film. Non-mechanical light deflection is achieved by altering the reflectance of a diffraction grating (an electro-optic method), an approach that creates new diffraction peaks that lie between those associated with the original grating spacing. This method for electro-optic diffraction is made practical by the supercapacitance exhibited at the interface between a layer of indium tin oxide (ITO) and a solution consisting of methylene blue dye ions dissolved in water. This interface was examined and measured to have a capacitance of 40 F/m2 with a corresponding reversible change in the reflectance of this interface of greater than 50%. The capability of this method to reversibly deflect light was experimentally verified by fabricating test cells consisting of two glass plates, each coated with a thin film of ITO. A solution of methylene blue dye ions dissolved in water was sealed between the two plates. Electro-optic diffraction modulation was demonstrated by patterning one of the two ITO films into an interdigitated design, done via standard photolithography techniques for initial experimental verification, and via focused ion beam milling for sub-micron scale electrodes. An electrical potential difference was applied between the interdigitated ITO electrodes and the radiant flux of the newly created diffraction peaks was measured. The light distribution that reflected by means of total internal reflection from the ITO/solution interface was measured to reversibly shift 0.7% of the incident light to new diffraction peaks. This approach may be useful in applications where large diffractive deflection angles are required and alternate beam-steering methods are impractical. ii Preface All of the work presented in this thesis was conducted in the Sustainability Solutions Applied Physics Laboratory (SSAP Lab) at the University of British Columbia, Point Grey campus. The work in this thesis was based upon an optical design developed by Lorne Whitehead and John Huizinga1. This thesis describes and tests an improvement of this design. The research presented in chapters 4, and especially 5 has been published in the Journal of Applied Optics [Radel J. C. and Whitehead L. A., “Electrically controlled diffraction employing electrophoresis, supercapacitance, and total internal reflection”]. I was the lead investigator for this work, responsible for the design of experiments, experimental apparatus construction, data collection, analysis, and manuscript composition. Lorne Whitehead was the supervisory author and was involved throughout all stages of the project in concept formation, experimental design, and manuscript edits. I was the lead investigator for the research described in chapter 6 (unpublished). Dan Bizzotto was involved in concept formation and experimental design of this work, and also assisted with the analysis of data collected. Lorne Whitehead was my research supervisor and was involved in concept formation, experimental design, and manuscript edits. I was the lead investigator for the research described in chapter 7 (unpublished). I was responsible for the design, construction, and testing of the experiment, analysis, and manuscript composition. Certain portions of experimental construction were performed at the Centre for High-Throughput Phenogenomics. Owen Gethin was involved in these portions of experimental construction. Lorne Whitehead was my research supervisor and was involved in concept formation, experimental design, and manuscript edits. Additional advice and guidance was provided by my supervisory committee and project collaborators, Jeff Young, Dan Bizzotto, Carl Hansen, Andrzej Kotlicki, Michele Mossman, and John Huizinga. iii Table of Contents Abstract .......................................................................................................................................... ii Preface ........................................................................................................................................... iii Table of Contents ......................................................................................................................... iv List of Tables ............................................................................................................................... vii List of Figures ............................................................................................................................. viii List of Abbreviations ................................................................................................................. xiv Glossary ........................................................................................................................................xv Chapter 1 : Introduction ...............................................................................................................1 1.1 Light Beam Steering ....................................................................................................... 1 1.2 Methods for Light Beam Steering................................................................................... 2 1.3 Absorption-Based Electro-Optic Diffraction .................................................................. 5 1.4 Electrophoresis-Based Electro-Optic Diffraction ........................................................... 8 1.5 Structure of this Thesis ................................................................................................. 10 Chapter 2 : Background ..............................................................................................................13 2.1 Debye Length ................................................................................................................ 13 2.2 Electrophoresis .............................................................................................................. 13 2.3 Electric Double Layer Structure ................................................................................... 14 2.4 Electrochemical Reactions in Electrolytic Capacitors .................................................. 18 2.5 Supercapacitance........................................................................................................... 19 2.6 Reference Electrodes .................................................................................................... 19 2.7 Diffraction ..................................................................................................................... 21 2.8 Light Transmission through an Absorbing Medium ..................................................... 24 2.9 Fresnel Reflections........................................................................................................ 25 2.10 Total Internal Reflection ............................................................................................... 25 Chapter 3 : Experimental Methodology ....................................................................................28 3.1 Selecting the Candidate Absorber Molecule................................................................. 28 3.2 Experimental Techniques.............................................................................................. 31 3.2.1 Goniophotometry ...................................................................................................... 32 3.2.2 Spectroelectrochemistry ........................................................................................... 33 iv 3.2.3 3.3 Electrochemical Chronocoulometry ......................................................................... 34 Fabrication Techniques ................................................................................................. 36 3.3.1 Photolithography ...................................................................................................... 36 3.3.2 Focused Ion Beam Milling ....................................................................................... 37 3.4 Analytical Techniques .................................................................................................. 38 3.4.1 Huygens-Fresnel Based Calculations ....................................................................... 38 3.4.2 GSolver ..................................................................................................................... 39 3.4.3 Comparison of Results from Huygens-Fresnel Based Calculations and GSolver ... 40 Chapter 4 : Interface of ITO and Methylene Blue in Water ...................................................43 4.1 Design Requirements .................................................................................................... 43 4.2 Experimental Set-Up ..................................................................................................... 46 4.3 Fabrication Techniques ................................................................................................. 48 4.4 Experimental Results .................................................................................................... 49 4.5 Discussion ..................................................................................................................... 56 4.6 Summary ....................................................................................................................... 59 Chapter 5 : Electro-Optic Diffraction Grating Cell ................................................................60 5.1 Design Requirements .................................................................................................... 60 5.2 Experimental Set-Up ..................................................................................................... 63 5.3 Fabrication Techniques ................................................................................................. 66 5.4 Results ........................................................................................................................... 67 5.5 Comparison of Experimental Results with Model Predictions ..................................... 72 5.6 Summary ....................................................................................................................... 78 Chapter 6 : ITO/MB-H2O Interface Analysis Using Electrochemical Methods ....................80 6.1 Spectroelectrochemistry................................................................................................ 80 6.1.1 Experimental Design ................................................................................................ 80 6.1.2 Results ...................................................................................................................... 83 6.1.3 Analysis .................................................................................................................... 86 6.2 Double Potential-Step Chronocoulometry .................................................................... 90 6.2.1 Experimental Design ................................................................................................ 91 6.2.2 Experimental Results ................................................................................................ 92 6.2.3 Analysis .................................................................................................................... 95 v 6.3 Summary of the Phenomenon ....................................................................................... 99 Chapter 7 : Electro-Optic Large-Angle Diffraction ...............................................................100 7.1 Design Requirements .................................................................................................. 100 7.2 Experimental Set-Up ................................................................................................... 105 7.3 Sample Fabrication ..................................................................................................... 108 7.3.1 Electrode Preparation ............................................................................................. 108 7.3.2 Focused Ion-Beam Milling ..................................................................................... 114 7.4 Experimental Results .................................................................................................. 118 7.5 Discussion ................................................................................................................... 125 7.6 Summary ..................................................................................................................... 127 Chapter 8 : Conclusion ..............................................................................................................128 References ...................................................................................................................................132 Appendices ..................................................................................................................................141 Appendix A : Ion Beam Milling Techniques......................................................................... 141 Appendix B : Huygens-Fresnel Based Calculations ............................................................... 146 vi List of Tables Table 3-1: Absorption peaks for different species of methylene blue .......................................... 30 Table 4-1: Net charge per area of working electrode during four characteristic time periods ..... 53 Table 5-1: Diffraction peak flux fraction values (ratio of measured flux to incident laser flux) . 68 Table 5-2: Diffraction peak flux fraction for empty cell (ratio of measured flux to incident laser flux) ............................................................................................................................................... 73 Table 5-3: Flux fractions for cell with MB-H2O (ratio of measured flux to incident laser flux) . 75 Table 6-1: Composition of methylene blue monomer and dimer used for fitting ........................ 90 Table 6-2: Linear fit values for charge accumulation through cell vs. the square root of time .... 97 Table 7-1: Net charge area density through a planar and diffraction grating cell ...................... 121 vii List of Figures Figure 1-1: A liquid crystal screen can control the transmission in different regions to create a diffraction grating. .......................................................................................................................... 4 Figure 1-2: Schematic of interdigitated electrodes. A conductive film (black) is patterned into an interdigitated design on a non-conductive substrate (gray). ........................................................... 9 Figure 1-3: Controlled total internal reflection as a means of electro-optic diffraction. Applied potentials to interdigitated electrodes attract light-absorbing particles, creating a diffraction grating with a new spatial frequency. ........................................................................................... 10 Figure 2-1: Electric double layers in an electrolytic capacitor. The potential difference from that of the bulk solution decays exponentially with distance from the electrode surface with a characteristic decay distance equal to the Debye length. .............................................................. 16 Figure 2-2: A more elaborate model of the electric double-layer, known as the GCS model, in an electrolytic capacitor. The potential drops linearly over a compact layer of ions, and then approximately exponentially over a diffuse layer of ions. ............................................................ 17 Figure 2-3: Equivalent circuit representation of an electrolytic capacitor .................................... 18 Figure 2-4: Diffraction occurring out of plane of incident light. In (a), light strikes an array of grooves parallel to the axis of the diffraction pattern. In (b), light strikes a diffraction grating under a prism................................................................................................................................. 23 Figure 3-1: Methylene blue and chlorine ions. Estimated dimensions of the molecule are given; the dimension not shown (rising out of this page) is estimated to be about 0.33 nm. .................. 29 Figure 3-2: Molecular structure of the clear, neutral, leucomethylene blue molecule ................. 30 Figure 3-3: Dimer form of methylene blue. The trimer form contains one additional methylene blue ion.......................................................................................................................................... 31 Figure 3-4: Graphical depiction of a user-defined diffraction grating in GSolver. The diffraction grating depicted here consists of four materials: a superstrate (white), substrate (gray), and two intermediate materials with variable thicknesses and widths (shown in hashed gray and white). 40 Figure 3-5: Huygens-Fresnel results vs. GSolver results. GSolver results contained some outliers (some of these values too large to be shown in this graph)—likely resulting from some unknown numerical errors. ........................................................................................................................... 41 viii Figure 4-1: Planar cell design. In (a), a schematic of the experimental cell is shown. In (b), a photo of an experimental cell is shown, with a laser beam reflecting from the working electrode interface......................................................................................................................................... 44 Figure 4-2: Optical arrangement used for planar cell measurements. Incident laser light is focused onto the working electrode/solution interface. Reflected light from this interface is measured with a photodetector located in an integrating sphere. ................................................. 47 Figure 4-3: Circuit used for applying potentials to planar cell. An operational amplifier is used, calibrated to have a gain of -1 V and a DC offset of 0 V. ............................................................ 48 Figure 4-4: Circuit diagram for planar cell ................................................................................... 50 Figure 4-5: Current density through planar cell when chlorine ions are attracted to the working electrode. Labels indicate the integrated current values for time periods when a 1 V potential difference was applied between electrodes, and when no potential difference was applied. Arrows indicate the relevant axes for each data set. ..................................................................... 51 Figure 4-6: Current density through planar cell when methylene blue ions are attracted to the working electrode. Labels indicate integrated current values during time periods when a -1 V potential difference was applied between electrodes, and where no potential difference was applied. .......................................................................................................................................... 52 Figure 4-7: Applied potential sequence to the planar cell. Inset shows a single potential pulse. The scaling of the inset has been altered for visualization purposes. ........................................... 54 Figure 4-8: Measured reflected flux fraction from planar cell. Inset shows the flux fraction when the -1 V pulse was applied to the cell. The axes of the inset are not to scale. .............................. 55 Figure 4-9: Charge dissipated from planar cell after applied potentials were set to zero. Charge from the cell increased significantly above potentials of 0.6 V. A slight drop in charge dissipation was observed above 0.95 V. ....................................................................................... 56 Figure 4-10: Effective capacitance of the electrochemical cell – the charge dissipated from the cell when applied potentials were set to zero was divided by the applied potential. .................... 57 Figure 5-1: Electro-optic diffraction grating cell .......................................................................... 61 Figure 5-2: Dimensions of diffraction grating .............................................................................. 62 Figure 5-3: Circuit schematic for 10 µm diffraction grating cell electrodes. An operational amplifier was used to enable the production or large currents. A second inverting operational amplifier was used to produce a second equal and opposite applied potential sequence. ............ 63 ix Figure 5-4: Alignment components for diffraction grating cell.................................................... 64 Figure 5-5: Gray-scale photograph of diffraction peaks reflected from diffraction grating cell .. 66 Figure 5-6: Interstitial diffraction peak flux fraction values. The measured diffraction peak was located at an angle of 1.9° +/- 0.1° with respect to the 0th order beam. Arrows indicate relevant axis for each data set. .................................................................................................................... 68 Figure 5-7: Applied potential sequence to one of two diffraction grating electrodes .................. 70 Figure 5-8: Measured interstitial diffraction peak flux fraction. Measured diffraction peak was located at an angle of 1.9° with respect to the 0th order beam. ..................................................... 71 Figure 5-9: Graphical depiction of model of diffraction grating when experimental cell was empty............................................................................................................................................. 73 Figure 5-10: Diffraction peak flux fractions for empty cell ......................................................... 74 Figure 5-11: Graphical depiction of diffraction grating when experimental cell was filled with MB-H2O solution. ......................................................................................................................... 75 Figure 5-12: Normalized diffraction peak flux fraction values for cell filled with MB-H2O (no potentials applied to cell) .............................................................................................................. 76 Figure 5-13: Graphical depiction of diffraction grating when an applied potential of -1 V was applied to the interdigitated electrodes of an experimental cell. .................................................. 77 Figure 6-1: Planar cell used for spectroscopic measurements. The working electrode area in contact with solution was 1 cm by 1 cm. A sheet of carbon nanofoam is used as the largecapacitance counter-electrode. ...................................................................................................... 81 Figure 6-2: Optical arrangement used for spectroscopic measurements ...................................... 83 Figure 6-3: Measured absorption coefficients –ln(I/Io) for the methylene blue in water solution (0.1 M). Error bars shown in light-gray. ....................................................................................... 84 Figure 6-4: Measured absorption coefficients –ln(I/Io) for the methylene blue in water solution with different potentials applied to cell. Error bars shown in light-gray. A running average (over 10 nm) is depicted for data measured when -1 V and -1.5 V were applied. ................................. 85 Figure 6-5: Measured absorption coefficient when a potential was applied to the cell –ln(I/Io)V less the absorption coefficient when no potential was applied –ln(I/Io)o. Running averages of the measured data (over 10 nm) are depicted. Most absorption occurs between 575 nm – 775 nm, with a weak absorption peak around 780 nm also observed. ........................................................ 86 x Figure 6-6: Absorption cross sections for monomer and dimer forms of methylene blue obtained from prior published work. ........................................................................................................... 87 Figure 6-7: Initial absorption coefficients –ln(I/Io) fit as sum of methylene blue monomer and dimer absorption cross sections .................................................................................................... 88 Figure 6-8: Measured absorption coefficients when a potential was applied to the –ln(I/Io)V less the absorption coefficients when a potential of 0 V was applied –ln(I/Io)o and a chi-square fit of this data using the absorption spectra of methylene blue monomer and dimer ............................ 89 Figure 6-9: Potential sequence applied to the planar cell for double potential-step chronocoulometry. Potential pulses were applied for a period of four seconds. Scale of inset altered for visualization purposes. ................................................................................................ 92 Figure 6-10: Measured reflected flux fraction for four different MB/NaCl solutions. Measurements were taken with the same experimentally cell, performed sequentially in order of increasing MB concentration. ....................................................................................................... 93 Figure 6-11: Measured flux fraction values dropped temporarily when applied potentials were removed. Dotted lines indicate the flux fraction values before the potential pulse was applied. Arrows indicate the relevant axes for each data set. ..................................................................... 95 Figure 6-12: Accumulated charge through planar cell during chronocoulometry experiment ..... 96 Figure 7-1: Electro-optic diffraction grating cell for large-angle diffraction. The ITO film on the top substrate has been patterned into two electrically isolated electrodes in an interdigitated design. Electrical contact was made with these electrodes using silver epoxy (not shown). ..... 101 Figure 7-2: Photograph of diffraction grating cell filled with methylene blue in water solution. The top substrate consists of an ITO film patterned into an interdigitated design. Electrical contact is made with these electrodes using silver epoxy, and the red and yellow wires shown above. The bottom electrode is maintained at ground, and connected to via silver epoxy and the black wires shown above. ........................................................................................................... 102 Figure 7-3: Grating pitch dimensions and estimated flux fraction of 1st order and interstitial order diffraction peaks when potentials of -1 V are applied to interdigitated electrodes. ................... 103 Figure 7-4: Interdigitated diffraction grating designed with a primary spatial frequency (800 nm pitch) and an additional secondary spatial frequency (effective pitch of 8 µm) component to aid the alignment process .................................................................................................................. 104 Figure 7-5: Optical arrangement for 800 nm pitch diffraction grating measurements. .............. 106 xi Figure 7-6: ITO coated glass electrode preparation. In (a), ITO film has been removed via laser cutter to leave a 200 µm thick ITO film bridge electrically connecting the film. In (b), a cross section of this electrode is depicted with exaggerated ITO film thickness for illustrative purposes. In (c), silicone has been applied to the electrode leaving only a small portion of the ITO bridge exposed. ...................................................................................................................................... 111 Figure 7-7: SEM image of ITO coated glass electrode before milling. In (a), silica particles are bonded to the ITO film. In (b), the ITO surface is clean and ready for ion beam milling.......... 113 Figure 7-8: SEM images of milled interdigitated design in ITO coated glass electrode. Light regions are ITO film, while dark regions indicate locations where the focused ion beam removed ITO film, exposing glass. ............................................................................................................ 115 Figure 7-9: SEM image of milled interdigitated design, which separates the ITO film into two isolated electrodes. ...................................................................................................................... 117 Figure 7-10: Unknown film deposited on ITO after SEM imaging............................................ 118 Figure 7-11: Potential sequence applied to diffraction grating (a), and the measured flux fraction of the interstitial order peak (b). The angle of this diffraction peak with respect to the 0th order beam was 33°. ............................................................................................................................. 119 Figure 7-12: Flux fraction of interstitial order exhibiting a short dynamic response (< 50 ms). Applied potential to one interdigitated electrode was -1.75 V (depicted here as a positive potential for ease of viewing), while the applied potential to the second interdigitated electrode was 0.44 V. ................................................................................................................................. 120 Figure 7-13: Circuit diagram used to apply potentials to diffraction grating cell. The large-area counter electrode was always grounded, while two different potential sequences were applied to the interdigitated electrodes. ....................................................................................................... 122 Figure 7-14: Applied potentials sequence to the 800 nm pitch diffraction grating. Inset not to scale............................................................................................................................................. 123 Figure 7-15: Measured diffraction peak flux fraction for 800 nm pitch diffraction grating. Arrows indicate the relevant axes for each data set ................................................................................. 124 Figure 7-16: Measured diffraction peak flux fraction for 800 nm pitch diffraction grating. Arrows indicate relevant axes for each data set. ...................................................................................... 125 Figure A-1: Example of a 4 x 4 bitmap ...................................................................................... 143 xii Figure A-2: FIB milling of a 15 nm thick ITO film on glass. The desired pattern was an interdigitated pattern. .................................................................................................................. 144 Figure A-3: FIB milling of 15 nm ITO printed on glass using only one pass of the beam. Light areas indicate unaltered ITO, while dark areas in the image indicate areas where the ITO has been removed with the ion beam, revealing the glass underneath. ............................................. 145 Figure B-1: Two Huygens-Fresnel wavelets separated by a distance x...................................... 148 Figure B-2: Multiple Huygens-Fresnel wavelets constructively interfering to create a wavefront ..................................................................................................................................................... 149 Figure B-3: Two groups of wavelets with a phase varying periodically over a distance d ........ 149 Figure B-4: The diffraction grating plane composed of four groups of wavelets ...................... 152 Figure B-5: Reflection and transmission of the electric field ..................................................... 154 Figure B-6: Multiple reflections and transmissions of the electric field .................................... 155 Figure B-7: Optical path difference ............................................................................................ 156 Figure B-8: Single pitch of diffraction grating ........................................................................... 157 Figure B-9: Diffraction grating pitch for new diffraction peaks ................................................. 158 xiii List of Abbreviations Ag/AgCl/KCl – silver electrode coated with silver-chloride immersed in a saturated solution of potassium chloride in water CD – compact disc DAQ – data acquisition DC – direct current DMD – digital micromirror device DVD – digital video disc FIB – focused ion beam GCS – Gouy-Chapman Stern GLAD – glancing-angle deposition ITO – indium tin oxide ITO/Cl-H2O – the interface of ITO and a solution of chlorine ions dissolved in water. ITO/MB-H2O – the interface of ITO and a solution of methylene blue ions dissolved in water. LMB – leucomethylene blue MB – methylene blue dye MEMS – microelectromechanical systems MB-H2O – solution of methylene blue dye ions dissolved in water SAM – self-assembled monolayer SEM – scanning electron microscope TIR – total internal reflection UBC – University of British Columbia UV – ultraviolet xiv Glossary Adsorption – adhesion of atom, ion, or molecule to a surface Dimer – a chemical structure consisting of two identical molecules, in this thesis the term dimer is used to refer to the form of methylene blue consisting of two methylene blue ions. See Figure 3-3. Electrolyte – a substance that has been dissolved into ions in a solvent. Supercapacitor – electrolytic capacitor with more than 10 times the capacitance of a doublelayer capacitor. Typically, per area of electrode, its capacitance is more than 1 F/m2. Electrophoresis – movement of ions in a solvent under the influence of an electric field. Interdigitated electrodes – design of two interleaved electrodes. See Figure 1-2. ITO/MB-H2O – the interface of ITO and a solution of methylene blue ions dissolved in water. ITO/Cl-H2O – the interface of ITO and a solution of chlorine ions dissolved in water. Leucomethylene Blue – Oxidized form of methylene blue. Neutral in charge and does not absorb visible light. See Figure 3-2 Monomer – a chemical ion or molecule capable of chemically bonding with other monomers to form a dimer, trimer, or polymer. See Figure 3-1. Polymer – a chemical structure consisting of repeated molecules. It is used to refer to a methylene blue ion consisting of many different methylene blue monomers. Self-Assembled Monolayer – assembly of molecules adsorbed on a surface Total Internal Reflection – total reflection of light from the interface of two mediums, where light propagating through a medium with a greater index of refraction strikes a medium with a smaller index of refraction. Trimer – a chemical structure consisting of three identical molecules. It is used to refer to three methylene blue ions. Wavelets – point wave-like oscillators used in the Huygens-Fresnel principle xv Chapter 1: Introduction This thesis describes the development of a new method for steering a light beam, using a technique known as electrically-controlled diffraction. Before delving into how this method works and how it was developed, a background of what light beam steering is, how it is used, and a description of existing methods will be given. 1.1 Light Beam Steering The first light beam steering devices were likely created over 6,000 years ago with polished stones. These stones were used as mirrors to look at one’s own reflection. Light beam steering devices are now used for many purposes in a variety of fields. Today, light beam steering is required in a number of important applications, including telecommunications2, freespace communications3, laser radar systems4, industrial laser drilling and cutting, and data writing and retrieval systems5. In telecommunications, the industry has increasingly moved towards sending data via lasers along fiber-optic networks. Light beam steering is used in fiber optic networks to route many light signals among many different cables using a single device, in order to reduce complexity and costs. The telecommunications industry has also considered using light beam steering to send information to private homes wirelessly using lasers to reduce infrastructure costs6. Information sent through air or empty space is known as free-space communication. Free-space communications systems are used when wired connections are impractical or, in some cases, impossible, such as for communications with satellites and spacecraft. In freespace communications, information is transferred via electromagnetic radiation, and the range of effective communication depends in part on the beam dispersion (how quickly the signal spreads out)7. Lasers are used to increase the effective distance for free-space communications, and these systems require precise beam steering to work. Laser remote sensing systems, referred to as LIDAR (a portmanteau of light and radar), use beam steering to remotely detect objects with light. These systems work by directing a beam, usually an infrared laser beam, towards an object and then detecting the reflected signal. The reflected signal can be used to accurately determine the distance to an object. LIDAR is useful for creating high-resolution geographical maps, and has been used in atmospheric science to measure clouds in the sky8. 1 Light beam steering is also used for industrial purposes, such as for laser cutting and engraving. In these applications, a high-intensity laser beam is directed at a material to ablate a portion of the material. These machines rapidly scan the laser beam over the material in a preset pattern to cut it, or to engrave on its surface. High precision of the direction of the laser beam is necessary in order to effectively cut or engrave the materials. New types of data writing and receiving systems also rely on beam steering. One new field is known as holographic data storage, which stores data in the volume of a material, rather than just on its surface (such as is done for CDs and DVDs). These systems require two laser beams to read and write to the material. These data storage systems require fast beam steering in order to write and read data quickly. Light beam steering is used in many applications, but the way in which the steering is achieved varies between fields. Some fields use mechanical means, such as mirrors9 to direct the laser beam, while others use non-mechanical means. There still remain many possibilities for improvement to the methods of light beam steering for all of these fields. 1.2 Methods for Light Beam Steering The requirements of a light beam steering device vary based on application, but the ideal device can steer a beam quickly over a large angular operating range, while being efficient, inexpensive, and compact. Current devices, such as those using mirrors and microelectromechanical systems, use mechanically moving parts to steer a light beam. Other devices, such as those that use electro-optics10, liquid crystals11, or acoustic-optics12, have no moving parts, or rely only on very small-scale motion. These mechanical and non-mechanical systems are briefly discussed here. Light beam steering can be achieved at large size-scales using mirrors. Industrial laser cutting and engraving machines use mirrors to direct the laser beam13. These mirrors are typically driven with electric motors, although they can also be driven with smaller actuators such as piezoelectric crystals. If the beam needs to be steered in two dimensions, the laser reflects from two separately driven mirrors. This type of beam steering is advantageous at large size-scales due to its simplicity and its high speed, but it does not have a large angular operating range. 2 Mirrors are also used as beam steering devices in microelectromechanical systems (MEMS), which use moving parts that are typically of micrometer size-scales. These systems have achieved beam steering using arrays of mirrors or lenses. Digital micromirror device (DMD) technology14 uses large arrays of micromirrors, each approximately 20 µm in size, to control the direction of a light beam. These devices are currently used in projection technology15. Arrays of lenses steer light by altering the focal points of the lenses in the array. The focal points are altered by either modifying the refractive index or the physical shape of the lenses. Much work has been done on these types of systems, but they remain difficult to maintain and are cumbersome in size16. Electro-optic prisms change their refractive index to control the direction of a light beam. This is done using the Pockels effect, which is the change of the index of refraction of a material in the presence of an electric field17. Light deflection can be achieved when light traverses through a prism made of this material. The degree of light deflection induced from one of these prisms depends on the index of refraction of the material, and so the light deflection can be altered by controlling the electric field applied to the prisms. The amount of angular deflection from one of these prisms is extremely small, but a series of these prisms can be used to increase the net deflection18. Still, these electro-optic prisms suffer from a small angular operating range and require thousands of volts to operate19. Light beam steering through non-mechanical means can be done via electricallycontrolled diffraction. Electrically-controlled diffraction is achieved by altering the optical properties of a surface through the application of electric fields (electro-optic modulation). Figure 1-1 shows how a variable diffraction grating can be used to redirect light. Liquid crystals can be used to create such a diffraction grating. In a liquid crystal cell, the index of refraction of the cell is altered depending on the orientation of the liquid crystal. The change in the index of refraction, Δn, is about 0.15. The thickness, d, of liquid crystal needed to retard the light of free-space wavelength 𝜆𝑜 by 180° is given by the following formula20: 𝜆𝑜 2·Δ𝑛 =d 1 3 Liquid crystal screens Figure 1-1: A liquid crystal screen can control the transmission in different regions to create a diffraction grating. A liquid crystal screen is comprised of an array of liquid crystal cells. The orientation of the liquid crystal in each cell can be individually controlled, by applying different potentials across each cell. A diffraction grating can be made from a liquid crystal screen by orienting the liquid crystals in a periodic manner, thus causing diffraction of light transmitting through the screen. To achieve diffraction, using equation (1), the necessary thickness to retard light of wavelength 550 nm by 180° is about 2 µm. The liquid crystal grating cannot have a retarding region with a width less than the thickness of the cell, or the diffraction efficiency will be impractically small. For light of wavelength 550 nm, this limits the optical regions to roughly 2 µm. A diffraction grating with a spatial periodicity, known as the pitch of the diffraction grating, of 4 µm (each pitch consisting of one retarding and one non-retarding region) will have a first-order diffraction peak angle of only 8°. Hence, the inability to deflect light by more than a few degrees remains a limitation of liquid crystal electro-optic diffraction gratings. Acoustics can also be used to create electro-optic diffraction. These methods use surface or bulk waves in a material to diffract reflected light. The waves in these materials cause periodic 4 reflection, and so a diffraction grating is created with a pitch equal to the acoustic wavelength. Acoustic waves are created in the materials by applying electrical signals of a given frequency to physical actuators, such as piezoelectric crystals. Since the acoustic wavelength can easily be changed by applying a different electrical frequency to the actuators, these gratings are useful for redirecting light to many different angles. The limitation, however, is that the small wavelengths needed for large angular deflection require very high frequencies (solids with acoustic wavelengths equal to optical wavelengths would require of order 109 Hz), and so are energyintensive. Thus, like the liquid crystal gratings, they are impractical for deflecting light to angles of more than a few degrees. The devices that have been described in this section fail to meet all the requirements of an ideal beam steering device, and the development of an improved device would make new applications of beam steering practical. Most significantly, these methods for light beam steering use diffractive structures too large to deflect light to angles of more than 10°. 1.3 Absorption-Based Electro-Optic Diffraction The goal of the project described in this thesis was to develop a means for variable electro-optic diffraction at deflection angles greater than 20°. Variable diffraction at such angles requires reversibly altering the optical characteristics of surface features on a size scale comparable to, or smaller than, the wavelength of the light. An interesting possibility for doing this involves moving sub-optical sized absorptive particles, and a common way of doing that in liquids is by means of electrophoresis – the application of electric fields to cause small suspended particles to drift. There are many readily available particle systems in this sub-optical size range, including a wide variety of pigment systems, and dye molecules of various sizes. Overall, we seek five characteristics for particles in this system: 1. They should be stably charged; 2. They should remain in suspension, neither aggregating nor settling; 3. They should be sub-optical in size; 4. They should have enough absorption to create a strong diffraction effect; 5. Ideally, it should be possible to attract a sufficient surface density of them without requiring excessive electrical energy. 5 Three types of light-absorbing particles that could meet the first three criteria are pigment particles, dye ions, and metal ions that are reduced through electroplating. The first choice, pigment particles, have been studied for use in reflective displays based on frustrated total internal reflection21 but the typical absorption length at maximum particle density is several microns, which would not be consistent with characteristic #4 in the above list. Electroplating metal seems much more promising from that perspective, since very thin layers can block light. Consider copper as an example. The optical skin depth in copper is of order 10-8 m and this is equivalent to an optical cross section of about 8 x 10-22 m2 per electroplated atom22. Copper has two valence electrons, and so, per unit charge, the ratio of optical cross section to charge for electroplated copper atoms is approximately 0.003 m2/C. As will be discussed at several points throughout the thesis, the surface density of particles required to create a significant optical effect is the inverse of the particle optical cross section, and multiplying this by the charge per particle gives a required surface charge transfer of about 300 C/m2. Typical electro-plating voltages are of order one volt, so this means that a significant amount of energy would be required to switch the pattern – roughly 300 J/m2. The other possibility, which was explored in this project, was to use dye ions. These are much larger than metal ions (of order 1 nm in size) but thermal agitation is still readily able to keep them in suspension. There is a wide range of possible dyes with different absorption cross sections, but one fairly common dye, methylene blue, absorbs 650 nm light with an absorption cross section of 3 x 10-20 m2 and has a single positive unit charge. Its absorption cross section per unit charge is thus about 0.2 m2/C – about 70 times greater than that arising from electroplated copper and thus requires an energy per unit area of only about 5 J/m2 for switching. This seemed to be much more promising. It is helpful to consider some simple order of magnitude details about the feasibility of this idea. Using the reasoning mentioned above, the surface charge needed to create a substantial optical effect with methylene blue would be about 5 C/m2. Unlike the case of metal electroplating, where the charge transfers into the electrode, we at first assumed that the methylene blue would retain its charge in a dense region near the surface. In this case the voltage of this effective capacitor is simply equal to its internal field multiplied by the mean thickness of the charged region. It seemed very unlikely that the density of the dye in this region could exceed that of solid methylene blue, and so this placed a lower limit on the required 6 voltage of this capacitor. The lowest possible voltage estimate was obtained by assuming the highest possible relative dielectric constant in the region (that of water), and this yielded a required voltage of about 20 V. This would be impractically large because it would cause irreversible electrochemical degradation of the electrodes and would require 20 times more energy for switching than we had hoped. In short, it seems at first glance that this approach could not work. A method would be needed to avoid the requirement of such a large amount of charge per unit area of electrode. One potential method for overcoming this problem was the precursor to the research done for this thesis. In that work23, nanoporous conductive films were deposited on an insulating glass plate. The nanoporous films were used to produce a much greater area of electrode in contact with the solvent per unit area of the glass substrate, thus reducing the required amount of charge per unit area of electrode. That project was moderately successful; reversible changes in reflectance of as much as 35% were observed, although the films caused some scattering of the incident light and proved to be difficult to pattern and to keep operating. Additionally, in previous investigations with methylene blue electrophoresis, some anomalous observations had taken place in which significant optical effects were found at low voltages, which is inconsistent with the simple model mentioned above. That effect, unfortunately, had been difficult to reproduce. However during the initial phases of the research described in this thesis, we encountered the same phenomenon and this time it was possible to achieve better reproducibility. We proved that a planar electrode could store the required charge and achieve reflectance changes of 50% using methylene blue ions and with an applied potential of only 1 V. The mechanism through which this was accomplished was not clear, but a few things were initially known: the low voltage proved that particles held at this interface could not have been charged particles, the particles were absorbing a significant amount of light, and the process was reversible. In this sense it seemed at least partly analogous to electroplating. Indeed, it is known that methylene blue ions can be reduced and electroplated at a negative electrode, but the neutral deposited molecules, called leucomethylene blue, are known to be nearly transparent to visible light and the process is generally irreversible. Yet we were seeing significant optical absorption and an almost completely reversible electrochemical reaction. Despite the lack of a clear electrochemical explanation of the effect, it seemed likely to be useful for the intended purpose of this project, and it was decided to pursue it in greater detail. 7 Considerations of what may be occurring at this interface appear in more detail throughout this thesis, although no definitive answer has yet been developed. Since the primary goal of this thesis was to develop and understand the surrounding optical system, this mystery was not an impediment to success, but it strongly calls for further research in this field. 1.4 Electrophoresis-Based Electro-Optic Diffraction The optical system consisting of ITO and methylene blue dissolved in water was tested for optical application in a system that was capable of steering a light beam. This system was capable of reversibly creating diffractive structures of sub-visible size-scale, and hence could deflect light to angles up to 90°. This method is referred to as electrophoresis-based electro-optic diffraction, and will be described in detail in this section. A surface that reversibly absorbs light can be fabricated using transparent electrodes in contact with a solution containing light-absorbing, electrically-charged particles, and a diffraction grating can be created by forming the transparent electrodes into a design composed of interleaved digits, referred to as an interdigitated pattern (see Figure 1-2). Together, these form an electrophoresis-based electro-optic diffraction device. The reflectance and absorbance from the electrodes is controlled by altering the local concentration of the light-absorbing particles next to these electrodes. The concentration is increased by moving these particles through a fluid next to the electrodes by applying an electric field. This movement is known as electrophoresis. 8 Figure 1-2: Schematic of interdigitated electrodes. A conductive film (black) is patterned into an interdigitated design on a non-conductive substrate (gray). A new diffraction pattern with a spatial frequency half that of the spacing between the interdigitated electrode array can be created by increasing the local concentration of lightabsorbing particles next to every second interdigitated electrode (depicted in Figure 1-3). In the pattern depicted in Figure 1-3, only one such reduced spatial frequency pattern can be produced, but in principle, using multiple independently controlled electrodes, a variety of different spatial frequencies could be produced, each producing different diffraction peaks. For example, if the distance between electrodes is d, then attracting dye ions to alternating electrodes would create a spatial frequency of 1/d, while attracting dye ions to every third electrode (or two of every three electrodes) would create a spatial frequency of 2/(3d). For a grating of width D, spatial frequencies ranging from 1/d to 1/D could be created, with the possible number of spatial frequencies obtainable equal to the number of electrodes. The maximum spatial frequency of the electrode pattern is limited primarily by the patterning process used to create the electrodes, and so this method is capable of diffracting light to much larger angles than with liquid crystals. 9 Incident light Diffracted light Interdigitated electrodes Glass prism Glass Light-absorbing species in transparent liquid Light-absorbing species in transparent liquid New diffraction pattern Applied potential changes local species concentrations Glass prism Glass Light-absorbing species in transparent liquid + - + - + Light-absorbing species in transparent liquid Figure 1-3: Controlled total internal reflection as a means of electro-optic diffraction. Applied potentials to interdigitated electrodes attract light-absorbing particles, creating a diffraction grating with a new spatial frequency. The electrophoresis-based electro-optic diffraction method described in this section represents a precursor to the work reported here. This method was previously achieved using nanoporous films, although these films were found to be extremely difficult to pattern24. The work in this thesis describes a significant improvement of this method that eliminates the need for these films. This thesis describes how this improvement was achieved, briefly delves into some of the complex electrochemistry that makes this system practical, and then experimentally verifies its ability to reversibly deflect light to large angles. 1.5 Structure of this Thesis The work in this thesis proceeded in a somewhat recursive manner. For instance, experiments performed to better understand the electrochemistry at the electrode/solution interface were performed concurrently with experiments that demonstrated electro-optic 10 diffraction. Further, experiments were often modified and repeated after more was learned of the chemistry and physics of the system. As a result, in organizing thesis, it seemed that neither a strictly chronological, nor a strict conceptual organization scheme, would be optimal. Therefore, for added clarification the following outline describes the content of the thesis chapters and their relationship to one another. Chapter 2 presents some of the relevant general physical concepts necessary to understand the work in subsequent chapters. This includes descriptions of electrophoresis, the electric double-layer, electrochemical reactions, supercapacitance, chemical reference electrodes, and optical topics such as diffraction, light transmission through an absorbing medium, Fresnel reflections, and total internal reflection. Chapter 3 briefly introduces a diverse range of specific topics to help prepare the reader for the research described in the subsequent chapters, where more detail is provided. Section 3.1 provides a thorough description of the dye ion used in this work and why it was chosen. Section 3.2 describes some of the more significant experimental techniques used throughout this thesis, including goniophotometry, spectroelectrochemistry, and electrochemical chronocoulometry. Section 3.3 details two fabrication techniques, including photolithography and focused ion beam milling, which were used to pattern the ITO films used in this thesis. Lastly, Section 3.4 describes two methods used to analyze the diffraction patterns from experimental cells, including a numerical diffraction grating simulation program known as GSolver and a calculation based on the Huygens-Fresnel principle. Chapter 4 details experiments performed to determine the effective electrolytic capacitance of the interface of ITO and methylene blue ions dissolved in water, and the corresponding reversible change in reflectance of this interface. Chapter 5 describes an experiment performed to test whether this system could be used for electro-optic diffraction. The point of this experiment was not to achieve large-angle diffraction (a significantly more difficult experiment which was the final experiment for this work), but rather to learn how best to achieve electro-optic diffraction with electrodes at a sizescale of micrometers. This is presented as a first step leading toward electro-optic diffraction using electrodes at a sub-micrometer size-scale. Chapter 6 describes two electrochemical experiments used to analyze the interface of ITO and methylene blue dissolved in water, including an experiment which measured the spectrum of 11 light that was absorbed at this interface, and an experiment which analyzed the rate of charge accumulation through the cell under different applied potentials. This chapter was included after Chapter 5, and not earlier, because the information learned from these experiments was not fully taken into account until Chapter 7. In Chapter 7, the final experiments described in this thesis are presented, which demonstrate reversible electro-optic diffraction at an angle of 33°. Lastly, Chapter 8 provides a summary of the results from the previous chapters as well as commentary and suggestions for further research. 12 Chapter 2: Background Before continuing further with the description of this research, it is useful to first briefly review some key concepts that are directly relevant to the work described in this thesis. The topics covered in this section are necessarily diverse; their description here is simply intended to provide a helpful context for the remainder of the document. 2.1 Debye Length If a charged surface is placed in a medium consisting of mobile charge carriers, then the charge carriers in the medium will redistribute in response to the changed electric field. Carriers of like charge will be repelled away from the surface, while carriers of opposite charge will be attracted toward the surface. This redistribution of ions acts to damp, or screen, the electric field from the charged surface over a characteristic distance. In a solution containing dissolved ions, the characteristic length of this screening is known as the Debye length, 𝜆D , and can be estimated using the Debye formula25: 𝜀 o 𝜀 𝑟 𝑘𝐵 𝑇 𝜆D = √ 2𝑞𝑒 2 𝐼 2 where 𝜀o is the permittivity of free space, 𝜀r is the relative permittivity of the solvent, 𝑘𝐵 is Boltzmann’s constant, 𝑇 is the temperature of the electrolyte solution, 𝑞e is the magnitude of the charge of an electron, and 𝐼 is the density of ions in the solution (ions/m3). 2.2 Electrophoresis An electrolyte is a substance that ionizes when dissolved in a solvent. The motion of ions relative to the solvent when an electric field is applied is known as electrophoresis. The speed at which these ions travel depends on the strength of the electric field that is applied and the charge of the ion. The ratio of the speed of travel to the electric field strength is known as the electrophoretic mobility. When two electrodes are placed in contact with a solution containing electrolytes (referred to as an electrolyte solution), and a potential is applied between the electrodes, an electric field is created in the solvent. Initially the electric field is approximately uniform in the solution, equal to the applied potential divided by the distance between the electrodes. The electric field causes movement of the dissolved ions, with positive ions attracted to the electrode 13 at a lower potential, and the negatively charged ions attracted towards the electrode at a higher potential. These ions move via electrophoresis and begin to accumulate at the two electrodes. When large potentials are applied between the electrodes (> 1 V), the ions will chemically react with the electrode, at lower potentials there are little to no chemical reactions. 2.3 Electric Double Layer Structure When an electrical potential difference is applied between two electrodes in contact with an electrolyte solution, the accumulation of ions around the electrodes causes the net charge surrounding the electrodes to be non-zero. The structure of this layer of ions, known as the electric double-layer, together with the electrode, can be modelled as a capacitor known as a double-layer capacitor. The other electrode and the electric double-layer surrounding it form a second double-layer capacitor. The system consisting of two electrodes in contact with an electrolyte solution, each forming double-layer capacitors with the solution, is known as an electrolytic capacitor. In steady state, electric fields in a highly conductive material are always zero (because otherwise the mobile charges will rearrange to make the field zero), so for conductive electrodes in an electrolytic capacitor, all the charge in the conductor resides on the conductor’s surface. The Helmholtz model26 for double-layer capacitance proposes that the ions in the solution also reside near the surface of the electrode, although it does not describe the nature of the distribution. The result is two regions of equal and opposite net charge, the first within the electrode and extremely close to its surface, and the second, of opposite charge, within the solution and fairly near the electrode. We can define a characteristic distance d to represent the effective separation of these two charge distributions. Generally the distance d is much smaller than any relevant physical dimensions of the electrode such that this system is almost exactly the equivalent of a parallel plate capacitor, whose capacitance is given by the formula: 𝐶= 𝜀𝑜 𝜀𝑟 𝐴 𝑑 3 where 𝜀o is the permittivity of free space, 𝜀r is the relative dielectric constant of the material between the plates, A is the area of the electrode exposed to the electrolyte solution, and d is the separation between the parallel plates. The electric field generated between two plates in a parallel plate capacitor is given by the following formula: 14 𝐸⃗ = 𝑄 𝐴·𝜀𝑜 𝜀𝑟 𝑥̂ 4 where 𝐸⃗ is the electric field between the parallel plates, Q is the charge stored on one of the plates, and 𝑥̂ is a unit vector pointing from the plate of higher potential to the plate of lower potential. Although equation (3) generally refers to two charge distributions which are thin compared to the separation distance d, it applies equally well for thicker charge distributions for which d represents an effective average separation. The critical question for this system is how this average separation depends on the applied potential and the electrolyte concentration. The Helmholtz model does not take into account that the ions in the solution are not necessarily accumulated directly on the electrode surface. The Gouy-Chapman Theory for the structure of the double-layer provides a model for the distribution of ion density near the surface, as being determined primarily by the local electrical potential and the Boltzmann factor27. This means that the spatial distribution of ion density must obey the relation: 𝑛(𝑥) 𝑛𝑜 −𝑞·𝜙(𝑥) = 𝑒𝑥𝑝 ( 𝑘𝐵 𝑇 ) 5 where n(x) is the concentration of ions as a function of the distance x away from the electrode surface, no is the concentration of ions in the bulk solution, q is the charge of an ion, ϕ(x) is the local electrical potential at the distance x from the electrode surface (relative to the potential at the distance point where no is defined), kB is the Boltzmann constant, and T is the temperature of the solution. Importantly, ϕ(x) is determined by the laws of electrostatics and the density distribution n(x); the mathematical challenge is to find the function n(x) that satisfies both relations. A depiction of that model is shown in Figure 2-1. As previously discussed, an applied potential between two electrodes in contact with a solution containing dissolved ions causes ions to accumulate near the electrodes, forming an increased concentration of ions near the electrode surface. For electrode potentials less than about 50 mV, the potential in the solution drops exponentially away from the electrode surface with a characteristic length equal to that of the Debye length: −𝑥 𝜙(𝑥) = 𝜙𝑜 · 𝑒𝑥𝑝 (𝜆 ) 𝐷 6 15 where 𝜙𝑜 is the potential at the electrode surface, x is the distance from the electrode, and 𝜆𝐷 is the Debye length, as previously defined in equation (2). Figure 2-1: Electric double layers in an electrolytic capacitor. The potential difference from that of the bulk solution decays exponentially with distance from the electrode surface with a characteristic decay distance equal to the Debye length. 16 Figure 2-2: A more elaborate model of the electric double-layer, known as the GCS model, in an electrolytic capacitor. The potential drops linearly over a compact layer of ions, and then approximately exponentially over a diffuse layer of ions. The Gouy-Chapman model, as depicted in Figure 2-1, treats the ions as point particles and does not place any restriction on how closely they can approach one another or the electrode surface. Interestingly, however, at the voltages and bulk concentrations that are of interest in the work described in this thesis, that model is insufficient – the predicted Gouy-Chapman density values near the electrode would exceed that of ordinary solid materials. Stern first proposed a modification to the Gouy-Chapman model that takes the finite size of the ions into account28. It does so by modeling the distribution of ions as a compact layer of solvent molecules and adsorbed ions having a uniform solid-like density and a defined thickness on the electrode surface, and beyond it a diffuse layer that follows the Gouy-Chapman relation. This combined model is known as the Gouy-Chapman-Stern (GCS) model for the electric double layer. A depiction of the regions in the GCS theory for the electric double layer is shown in the top portion of Figure 2-2. This theory predicts that the potential in the solution drops linearly across 17 a compact layer of solvent molecules and adsorbed ions, and then exponentially across the diffuse layer to the potential in the bulk solution, as shown in the bottom portion of Figure 2-3. 2.4 Electrochemical Reactions in Electrolytic Capacitors The previously described models for the electric double layer ignore the effect of chemical reactions between the electrode and the electrolyte solution (known as electrochemical reactions when the reactions are induced by an electric field between the solution and the electrode). When electrochemical reactions occur, each electrode still acts as a capacitor, but current known as Faradaic current also flows from the electrode to the electrolyte solution. Thus, an electric double layer capacitor can be more generally modeled, from an electrical circuit perspective, as a capacitor with a parallel leakage resistance, which is infinite in the absence of electro-chemical reactions. This effective leakage resistance (known as the faradaic impedance) depends on many factors, such as the solution composition, the electrode material, and especially the applied potential. From an electrical perspective, both the electrode and the bulk solution have some resistance to the flow of electricity, and this can be modelled electrically as a resistor in series with the capacitor. Combining these two ideas, a circuit representation of an electric double layer capacitor is shown in Figure 2-3. Figure 2-3: Equivalent circuit representation of an electrolytic capacitor 18 Electrochemical reactions between an electrode and an electrolyte depend on the electrode material and electrolyte composition. For sufficiently low voltages these reactions do not occur, and typically they increase rapidly above a threshold voltage that varies significantly depending on the materials and concentrations, but is typically of order 1 V. For these reasons, electrolytic capacitors are usually operated using voltages under 1 V per cell. (Often discrete circuit capacitors will contain many cells operating in series, so that higher total voltages are possible.) 2.5 Supercapacitance Electrochemical reactions between an electrode and electrolyte can sometimes be used to increase the effective capacitance of an electrolytic capacitor. This can happen when an ionic species reduces or oxidizes in a reversible electrochemical reaction with the electrode surface. When a potential is applied in such an electrolytic capacitor, these ions can neutralize and deposit on the electrode surface. Since these molecules are neutral in charge, they can build up in a dense layer of molecules without adding to the cell voltage, thus increasing the capacitance, which is the ratio of charge stored to applied voltage. In this type of system, when the applied potential is removed, the reaction reverses, and the ions give back their charge to the electrode and return to their ionic forms. These systems can store far more charge than other electrolytic capacitors (10 – 100 times more) so they are referred to as supercapacitors. The energy in these systems is stored in the form of chemical energy, like a battery, so they are also often referred to as pseudocapacitors. 2.6 Reference Electrodes Analysis of an electrochemical cell often involves determining the potential difference between an electrode and the bulk solution in the cell. There is no way to do this directly, because any conductive probe placed in the bulk solution will itself form part of an electrochemical cell. For this reason, the common practice in electrochemical research has been to select certain well-characterized and reproducible electrodes as standard reference electrodes. A common example is a silver electrode coated with silver chloride and immersed in a solution of 1.8 x 1027 ions/m3 (3 M) potassium chloride in water (referred to hereafter as a Ag/AgCl/KCl electrode). The potential of the silver electrode with respect to the potassium 19 chloride solution is stable due to the reversible chemical reaction that occurs between the silver and chlorine ions. If the potential of the solution were somehow increased with respect to the silver electrode, then silver chloride on the silver electrode surface would reduce into solid silver and dissolved chlorine ions until the potential once again returned to its initial state. If the potential were lowered, chlorine ions would react with the silver electrode to from solid silver chloride. The chemical equation for this reversible reaction is: 𝐴𝑔𝐶𝑙(𝑠) + 𝑒 − ⇆ 𝐴𝑔(𝑠) + 𝐶𝑙 − Electrodes such as a Ag/AgCl/KCl electrode are useful for reference due to their stable potentials. For example, another electrode could be placed in the potassium chloride solution with the silver electrode and the potential between the new electrode and the silver electrode could be measured as a way of determining the potential difference between the electrode and the solution. This potential would have meaning only with respect to a Ag/AgCl/KCl electrode, so potentials of chemical reactions in electrochemistry experiments are reported with respect to a standardized reference electrode. To clarify with an example, in some electrochemical experiment, a researcher might determine that an ionic species reduces to a less charged form at a potential of -0.5 V with respect to a Ag/AgCl/KCl electrode. Another researcher using a similar solution but a different electrode material would then know that if they applied a potential between two electrodes immersed in this solution, that the ions would reduce when the potential of one of the electrodes with respect to a Ag/AgCl/KCl electrode was -0.5 V. Potentials between many different standardized reference electrodes are known, so the researcher could also use a different reference electrode and account for the potential difference. In many circumstances, one wants to measure the potentials of an electrode with respect to a solution different to that used in the reference electrode. To do this, the reference electrode is immersed in a container filled with a reference solution (potassium chloride in water for the case of the silver electrode), and this solution is connected to a different solution via a selective membrane that allows the passage of some species, but not others. A common example is a form of porous glass known as a glass frit, with pores large enough to allow the passage of ions, but too small for a significant amount of solvent to pass through. 20 2.7 Diffraction In the seventeenth century, it was observed that the shadow of a rod illuminated by a very small light cast an unusual shadow29. The edge of the rod’s shadow was not perfectly sharp, but was comprised of many bands of light barely noticeable to the naked eye. These bands of light could not be explained by treating light as rays that travel in straight lines (this treatment of light is referred to as geometrical optics), but was instead a result of the wave characteristics of light. These types of wave-related phenomena that cannot be explained using geometrical optics are known as diffraction effects. Diffraction effects are very small for objects much larger than the wavelength of light, but these effects become significant when the object interacting with light becomes smaller. A simple example of a structure where diffraction plays a large role is the reflectance of light from the surface of a CD. The colored patterns observed when viewing the surface of a CD arise from the incident light waves interacting with the very small pits on the CD’s surface. The light diffracts differently depending on the light’s wavelength, which is what gives rise to the iridescent appearance of the surface. Surfaces with ordered, repeating structures that interact with light are referred to as diffraction gratings. The spacing between the structures is known as the diffraction grating pitch. A laser beam that strikes a diffraction grating can split into several beams of light, and each of these beams is referred to as a diffraction peak and labelled with an integer, referred to as the diffraction peak’s order. The main reflected or transmitted beam from a diffraction grating is the 0th order peak. The beams closest to this beam are the 1st order, then the 2nd order, and so on. For a normal incident beam, the angle of these diffracted beams is governed by the diffraction grating equation: 𝑚 λ = 𝑑 · 𝑠𝑖𝑛(𝜃𝑚 ) 7 where m is the integer representing the order of the diffraction peak, λ is the wavelength of the light in the medium, d is the diffraction grating pitch, and θm is the angle of the mth order peak. In this thesis, diffraction gratings are formed in a manner that allows diffraction to be electrically modified. Although the diffraction gratings used are quite simple, the experimental results are directly applicable to more complex diffractive structures, such as those used in holography. When light diffracts, depending on the orientation of the diffraction grating, it can either diffract in the same plane as the incident light, like the diffraction shown back in Figure 1-3, or it 21 will diffract out of the plane of the incident light, like the diffraction shown in Figure 2-4. The diffraction principles still hold in these cases, but determining the direction of the diffraction peaks is less straight-forward in the three-dimensional case. As see in Figure 2-4(a), when light diffracts from a diffraction grating with grooves aligned parallel to the incident light beam, the diffraction peaks will lie outside the plane of the incident light. The diffraction beams will strike the perimeter of a circle centered on and perpendicular to the axis of the diffraction pattern. In Figure 2-4(b), light is observed diffracting from a diffraction grating lying just under a glass prism. Refraction of the light as it exits the prism distorts the diffraction pattern somewhat, but when the diffracted pattern is observed on a screen as shown, the observed pattern lies approximately on a circle. Mathematically speaking, one can calculate the directions of the diffracted rays of light by using the fact that the frequency of light as well as the component of momentum parallel to the surface and in the direction of light propagation do not change. Using the coordinate system from Figure 2-4(a), this means that for each diffraction peak, the y-component of the momentum does not change, but the z-components and x-components do change. For a light beam with a 0th order wave vector of 𝑘𝑦0 𝑦̂ + 𝑘𝑧0 𝑧̂ , the components of the mth order diffraction peaks, in a material with index of refraction of n, can be found using the following formulas30: 𝜆 𝑘𝑥𝑚 = 𝑚 𝑛·𝑑 8 𝑘𝑦𝑚 = 𝑘𝑦0 9 𝜆 𝑘𝑧𝑚 = √𝑘𝑧0 2 − (𝑚 𝑛·𝑑)2 10 In these equations λ is the wavelength of light in a vacuum and d is the diffraction grating pitch. 22 1st order diffracted beams Isometric View Screen z y x 2nd order diffracted beam Incident beam (a) Center 2nd order diffracted beam Diffraction pattern axis (b) Figure 2-4: Diffraction occurring out of plane of incident light. In (a), light strikes an array of grooves parallel to the axis of the diffraction pattern. In (b), light strikes a diffraction grating under a prism. 23 2.8 Light Transmission through an Absorbing Medium When light is absorbed as it traverses through a medium, this material is mathematically described as having a complex index of refraction. The intensity of light traversing through such a medium will decay exponentially with distance. If the absorbing medium consists of dye ions dissolved in a solvent, the exponential decay of the light intensity can be written in terms of the dye concentration, n, and the ion’s absorption cross section31, σ: 𝐼 = 𝐼0 e−𝑛𝜎𝑥 11 where I is the transmitted intensity, Io is the intensity of light entering the absorbing medium, and x is the distance the light traverses through the medium. This relationship is valid when the particles are smaller than a wavelength of light and therefore do not scatter the light, such as is the case for dye ions dissolved in a solvent. An equivalent form of equation (11) in the case where light has traversed through a planar slab of absorbing medium is: 𝐼 = 𝐼0 e−𝑛𝐴𝜎 12 where nA is the number of light-absorbing ions per area of the planar slab. To understand this form of the equation and why it is useful, consider a cube with sides of 1 m in length with 1000 light-absorbing particles contained within it. Light traversing perpendicularly through one of the faces of this cube and out the opposite face would traverse a total length through the cube of 1 m. The density of 1000 ions/m3 multiplied by the distance through the material of 1 m is the number of ions per area of material, 1000 ions/m2. If a portion of the ions in the cube were pulled toward the face of this cube the light was traversing through, then the ionic density becomes dependent on the location in the cube, but the ions per square meter of material would remain unchanged. This only works if the density changes only along the direction of light propagation, but cases analogous to this are common for electrolytic capacitors that pull a known amount of ions per square meter of material to the electrode-electrolyte solution interface, and so equation (12) is referred to often in this thesis. A consequence of equation (12) is that when light traverses a fixed distance through a medium with only one type of light-absorbing particle with an ionic concentration per cross section area that varies with time, then this concentration is proportional to the natural logarithm of the ratio of the transmitted intensity to the incident intensity. 24 𝐼 𝑛𝐴 ∝ ln (𝐼 ) 13 0 This relation is useful when correlating the reflection of light from an interface of an absorbing medium with the concentration of light-absorbing particles in the absorbing medium. 2.9 Fresnel Reflections When light strikes the interface between two media with different refractive index values, a portion of the light reflects and a portion of the light transmits through this interface. The reflected portion of this light is referred to as the Fresnel reflection. The amount of reflection can be calculated from the Fresnel equations as the absolute square of the electric field amplitude reflection coefficient. The experiments described in this thesis could have been carried out with any polarization. For consistency, it was decided to always use light polarized parallel to the material surfaces, a type of polarization referred to as s-polarized light. The reflected intensity for this polarization is32: 𝑅𝑠 = || 𝑛 𝑛1 𝐶𝑜𝑠(𝜃𝑖 )−𝑛2 √1−( 1 𝑆𝑖𝑛(𝜃𝑖 )) 𝑛2 𝑛 𝑛1 𝐶𝑜𝑠(𝜃𝑖 )+𝑛2 √1−( 1 𝑆𝑖𝑛(𝜃𝑖 )) 𝑛2 2 2 2 || 14 where 𝑅𝑠 is the intensity of the reflected light for s-polarization, and 𝜃𝑖 is the angle in the first medium between the incident light beam and the normal to the interface. This equation also holds when the index of refraction is complex (as is the case for an absorbing medium such as dye ions dissolved in a solvent). 2.10 Total Internal Reflection In certain cases the Fresnel reflection from an interface is equal to one (indicating total reflection of the incident light). This occurs when light propagating through a medium strikes a second medium with a lower index of refraction, and the light strikes this interface at a sufficiently large angle with respect to the normal vector of this interface. This case of complete reflection from an interface is known as total internal reflection. The smallest angle at which total internal reflection occurs is known as the critical angle. This angle is derived from Snell’s law: 𝑛 𝜃𝑐 = 𝑎𝑠𝑖𝑛 (𝑛2 ) 1 15 25 where 𝜃𝑐 is the critical angle, 𝑛1 is the index of refraction of the first medium, and 𝑛2 is the index of refraction of the second medium. The intensity of light that reflects by total internal reflection from an interface can be calculated using equation (14) as long as the angle of incidence and the indices of refraction of the two media are known. If the two media are not light absorbing (they have real indices of refraction), the reflected intensity for incident angles exceeding the critical angle will be 1. If one of the media has light-absorbing characteristics (it has a complex index of refraction), then the reflected intensity will be less than 1. When the second medium has light-absorbing characteristics, for example a solution of dye molecules dissolved in water, the real component of the index of refraction is largely independent of dye concentration. However, the imaginary component of the index of refraction is not, and can be calculated using the Beer-Lambert law: 𝜅= 𝑛𝜎𝜆𝑜 4𝜋 16 where 𝜅 is the imaginary component of the index of refraction for the electrolyte solution, 𝑛 is the concentration of dye ions in the electrolyte solution, 𝜎 is the absorption cross section of the dye ions, and 𝜆𝑜 is the wavelength of the light in a vacuum. This relation, when combined with the equation for Fresnel reflection, equation (14), can be used to determine the concentration of dye ions in the absorbing medium. A useful method for approximating the reflection of light undergoing total internal reflection from an interface such as ITO and dye ions dissolved in water is to make use of the fact that the light actually penetrates a very small distance into the solution of dye in water. This counter-intuitive penetration is an experimentally-verified property of light undergoing total internal reflection at an interface33. Since light penetrates a small distance into the absorbing medium, one can then estimate the amount of light absorbed based on the concentration of lightabsorbing ions in this material. Electrolytic capacitors with known capacitance per square meter of electrode material will pull, by means of electrophoresis, a known number of ions per area of electrode to the electrode/electrolyte solution interface. For dye ions dissolved in water with a known absorption cross section, equation (12) can then be used to approximate the amount of absorption of light at this interface. This method for estimating the absorption of light reflecting at this interface is only an approximation, and is valid only if the ions are much smaller than the wavelength of light, and are pulled to within a distance of the electrode much less than the 26 wavelength of light, but this is the case for the dye ions used in this work. One limitation of this model occurs at dye concentrations that approach the concentration of its solid form. At these extremely high concentrations one needs to account for interactions between ions, and the changes to the properties of the bulk medium (such as a change to the real component of the index of refraction). 27 Chapter 3: Experimental Methodology This chapter will detail how the candidate absorbing molecule was chosen, as well as experimental techniques, fabrication techniques, and analytical techniques that are referred to throughout this thesis. Specifically, it will outline some key characteristics of methylene blue dye and explain why it was chosen as the absorbing molecule, and will explain the experimental techniques used to measure and analyze the diffraction gratings, the fabrication techniques used to create the gratings, and the analytical techniques used to interpret the diffraction patterns from the experimental cells. 3.1 Selecting the Candidate Absorber Molecule The experiments in this thesis required an electrolytic capacitor with a transparent electrode and an electrolyte solution that, together with the electrode, could store an amount of charge much greater than typically can be achieved with normal electrolytic capacitances (typically in the range of 0.1 to 0.4 F/m2)34. ITO was chosen as the transparent electrode because it is widely used in the display industry as a transparent conductive layer and therefore is well characterized and readily available. The candidate absorbing molecule that was chosen was methylene blue. One of the reasons it was initially considered is that it is one of the most commonly used dyes in biology and chemistry; hence there is a lot of data available on this molecule. Methylene blue is also readily available and fairly non-toxic. For these reasons the interface of ITO and methylene blue dissolved in water, hereafter referred to as the ITO/MB-H2O interface, was first tested (described in detail in Chapter 4), and a charge storage greater than 40 C/m2 was observed with an applied potential of 1 V (in other words it had an effective capacitance greater than 40 F/m2). One other dye, Victoria Blue B obtained from Sigma Aldrich35, was tested in a similar manner and was measured to have a capacitance of only 0.1 F/m2, which is a typical expected value for electrolytic capacitors. The effective capacitance of the ITO/MB-H2O interface was several hundred times greater than this, (hence it is referred to as a supercapacitor throughout this thesis), and so methylene blue was chosen as the absorbing molecule. Supercapacitance of the ITO/MB-H2O interface was obtained reproducibly at concentrations of methylene blue greater than 6 x 1025 ions/m3 (0.1 M; near the solubility limit). As a result, an understanding of some of the complex chemistry of methylene blue at these concentrations was an important part of this work. 28 Methylene blue is an organic molecule with the chemical formula C16H18N3SCl (depicted in Figure 3-1). When dissolved in a solvent such as water, the molecule separates into a positively-charged, light-absorbing methylene blue ion, and a negatively-charged (not lightabsorbing) chlorine ion. 1.70 nm N 0.76 nm N + N S Cl - Figure 3-1: Methylene blue and chlorine ions. Estimated dimensions of the molecule are given; the dimension not shown (rising out of this page) is estimated to be about 0.33 nm. Methylene blue has many uses in biology and chemistry, most commonly as a biological stain or as a redox indicator. As a biological stain, methylene blue is used to increase the visual contrast in biological tissues, to aid in viewing with the aid of a microscope. Methylene blue also works as a redox indicator because it can reduce (lose a charge, i.e. gain an electron) into a molecule that does not significantly absorb visible light. If the molecule is present in its reduced form, it can oxidize (gain a charge) and turn into its charged, colored form. Redox indicators are used in chemistry to indicate whether certain types of chemical reactions have taken place36. The potential at which methylene blue reduces to its neutral form at an interface of ITO and methylene blue dissolved in water is -0.275 V with respect to a Ag/AgCl/KCl electrode37. The reduced, neutral form of methylene blue is known as leucomethylene blue. The chemical structure of leucomethylene blue is depicted in Figure 3-2. Leucomethylene blue does not absorb significantly in the visible spectrum38,39, but does absorb weakly in the near ultraviolet at 314 nm, and more strongly in the far ultraviolet 256 nm40. 29 H N N N S Figure 3-2: Molecular structure of the clear, neutral, leucomethylene blue molecule For the ionic concentrations used for the experiments in this thesis, methylene blue ions have been shown to bond with other methylene blue ions to make a single, larger ion41. It was possible these types of ions were the reason for, or contributed to, the large measured effective capacitances of the ITO/electrolyte solution interface. When two methylene blue molecules bond together in this way they are known as dimers, and a group of three is known as a trimer. Larger amounts of these groups, referred to as higher aggregates, have been theorized to exist as well. Studies of methylene blue at different concentrations have found that as the concentration increases, the percentage of methylene blue ions that exist in these forms also increases. At concentrations of methylene blue above 3.6 x 1025 ions/m3 (0.06 M), the molecules of methylene blue have been theorized to nearly all group into their trimer form42. These different forms of methylene blue all have unique absorption spectra. A few of the absorption peak wavelengths are given in Table 3-1. Table 3-1: Absorption peaks for different species of methylene blue Species Peak Wavelength (nm) Methylene blue 660, 614, 292 Leucomethylene blue 256 Dimer methylene blue 607, 658 30 + N N S N N N + S N Figure 3-3: Dimer form of methylene blue. The trimer form contains one additional methylene blue ion. Different forms of methylene blue have also been shown to bond to electrode surfaces in some electrolytic capacitors in a process known as adsorption. Adsorption between ions and electrode surfaces in electrolytic capacitors is not uncommon, but experiments have found that leucomethylene blue bonded especially strongly and irreversibly to an electrode surface. The amount of leucomethylene blue that bonded to the surface was measured to be unusually high, and was estimated to be 20 monolayers thick43. The amount of charge required to reduce the methylene blue on the surface in this manner was found to be 6 C/m2. However, since the adsorption and reduction of the methylene blue was irreversible this did not constitute a capacitor. For electro-optic diffraction, an irreversible process such as this is not useful, since being able to create and remove a diffraction pattern many times is necessary. For the experiments performed in this thesis, a similar amount of charge storage was observed on the electrode surface, however, unlike the irreversible leucomethylene blue adsorption, this charge was stored in a reversible process. 3.2 Experimental Techniques Several experimental techniques used throughout this thesis merit special consideration. This section describes how the measurements of the radiant flux values of light reflecting from the experimental cells were acquired, then describes the fabrication techniques that made use of a 31 focused ion-beam, and finally describes two electrochemical analysis methods used: spectroelectrochemistry and double potential step chronocoulometry. 3.2.1 Goniophotometry Measuring the diffraction patterns of light reflecting from the experimental cells was accomplished using a technique known as goniophotometry. Goniophotometry measures the angular distribution of light. This is often done using a detector such as a photodiode, whose location is moved while the current from the photodiode is measured and recorded to determine the distribution of light across a range of angles. For the measurements in this thesis, the diffraction peaks occurred at discrete angles, and so the detector did not need to be positioned at all angles within the range, but rather was placed at discrete calculated locations to measure each diffraction peak. Measurements were performed using a Melles Griot integrating sphere, a photodiode, and a current-to-voltage amplifier. The integrating sphere was placed in such a way that the diffraction peak was directed into the input port of the integrating sphere. Integrating spheres are typically used to mix up, or homogenize, incident radiation of varying angular spread or spatial irradiance. An integrating sphere was used in these experiments to measure the power of all of the light corresponding to a particular diffraction peak so any angular uncertainty or slight misplacement of the detector would have as little impact as possible on the measurement. Calibrated measurements of the power in a diffraction peak were not necessary, since the quantities of interest for the work in this thesis was the ratio of the power in each diffraction peak to the power of the incident laser beam. A silicon photodiode was located within the integrating sphere. The current from the photodiode was linearly proportional to the intensity of light striking the photodiode. The spectral response of the photodiode ranged from 350 nm to 1100 nm, although only 650 nm light was used for these measurements. The diameter of the measured diffracted beams (~ 2 mm in diameter at the location of measurement) was significantly less than the size of the integrating sphere input port diameter (1 cm), so the current from the silicon photodiode was proportional to the amount of power in the diffraction peak, a quantity known as the radiant flux of the light. Goniophotometry was also used to measure the wavelength-dependent angular distribution of light. These measurements were carried out using an integrating sphere, a fiber32 optic cable, and a spectrometer. For these measurements, a collimated white light beam (collimation angle 1.5°, diameter 2 mm) was directed at the experimental cells, and the wavelength-dependent reflectance was measured. This was done by directing the input port of the integrating sphere such that the reflected light entered the integrating sphere. Inside the integrating sphere, rather than a single photodiode, there was an aperture leading to a fiber optic cable. Light that struck this fiber optic cable was carried along the cable to an Ocean Optics USB2000+ spectrometer. An experimental setup used for such a measurement is described in Section 6.1.1, and depicted in Figure 6-2. Spectrometers use a diffraction grating to diffract the light to different angles based on the wavelength of light. An array of photodiodes detects the light, and the signal from these photodiodes is used to determine the spectral composition of the light44. 3.2.2 Spectroelectrochemistry A few basic electrochemical analytical techniques were used in this thesis in order to begin an analysis of the different processes occurring at the interface of ITO/MB-H2O. One of these techniques is known as spectroelectrochemistry. Spectroelectrochemistry is a technique whereby the wavelength-dependent reflection from or transmission through from an electrode or electrode/electrolyte solution interface is measured as a function of the applied potential. This is done by measuring the reflectance of an electrode using a spectrometer and comparing it to known wavelength-dependent absorption characteristics of different ions to determine the chemical species on or near the electrode. These measurements are often done on electrodes that have been removed from electrolytic cells to simplify these measurements. They are not able to measure the absorption properties of the bulk electrolyte solution itself, but they are capable of measuring the absorption properties of any ions that were adsorbed onto the electrode surface. When spectroelectrochemistry is performed on electrodes removed from electrolytic cells they are referred to as ex situ techniques. When these techniques are used on an electrode still submerged in the electrolyte solution, they are referred to as in situ techniques. In this thesis, in situ spectroelectrochemistry was performed on an electrochemical cell illuminated by a collimated white light source. The collimated white light was directed at the interface of ITO and methylene blue ions dissolved in water, at an angle where the light beam reflected from this interface by means of total internal reflection. The reflection of the light was 33 measured using goniophotometry, and the wavelength dependence of the reflection was compared to the known absorption characteristics of methylene blue ions. Different potentials were then applied to the experimental cell and the reflection was measured once again. The ratio of the measured reflection when a potential was applied to the measured reflection when the electrodes were electrically connected was used to infer the change in the chemical species at the ITO-MB-H2O interface when this interface was storing charge. This provided information on the chemical species pulled to this interface, information which was useful for determining the mechanism for the supercapacitance. 3.2.3 Electrochemical Chronocoulometry Another common electrochemical technique is chronocoulometry. It involves applying electrical potential steps to electrolytic cells while measuring and recording the resulting electrical currents passing through the cell. Next, the potentials are removed while the currents through the cell are once again measured and recorded. The currents through the cells during these time periods are then mathematically integrated with respect to time to determine the charge that had passed through the cells during that time period. To interpret the charge flow through electrochemical cells, an important aspect of electrolytic capacitors needs to be taken into account. An electrolytic capacitor consists of two capacitors in series, each one consisting of the interface of an electrode and an electrolyte solution. This can make interpretation of the charge flow through a cell difficult, because it can be unclear as to the relative contribution of these two interfaces. However, if one of the interfaces has a much greater capacitance than the other, then the amount of charge flow through the cell is limited by the smaller capacitance interface. This follows the series capacitance formula: 1 −1 1 𝐶𝑁𝑒𝑡 = (𝐶 + 𝐶 ) 1 2 17 so that the following holds: 1 1 −1 lim𝐶2 →∞ (𝐶 + 𝐶 ) 1 2 = 𝐶1 18 where CNet is the net capacitance of the electrolytic cell, and C1 and C2 are the capacitances of each of the electrode/electrolyte solution interfaces. If the capacitance of one of these electrodes 34 is substantially greater than the other, then the net capacitance is approximately equal to the capacitance of the smaller electrode/electrolyte solution interface. This effect can be used to simplify the analysis of an electrochemical cell by intentionally making the capacitance of one of the electrode/electrolyte solution interfaces substantially greater than the other. This can be done by making the area of one of the electrodes that is in contact with the electrolyte solution much greater than the other electrode. By designing a cell in this way, the charge flow through the cell will primarily depend on only the smaller-area electrode, referred to as the working electrode. The charge flows through electrochemical cells were analyzed with respect to time during a few characteristic time periods, such as the time periods when a potential is applied or removed. For instance, if charge was flowing from the electrode to the electrolyte solution via some unknown electrochemical reaction, and there were nothing inhibiting the charge flow other than the presence of a certain chemical species near the electrode surface, then the rate of the reaction will depend on how frequently the ions come in contact with the electrode. Before the charging of the electric double-layer near the electrode surface, the ions are pulled towards the electrode by means of electrophoresis. After this capacitor is fully charged, however, electrophoresis ceases and only the random thermal motion of ions due to diffusion cause ions to interact with the electrode surface. If chemical reactions occur when these ions come in contact with the electrode, then the current through the electrolytic cell resulting from these reactions will be governed by diffusion, which is described by the Cottrell equation45: 𝑖𝑑 (𝑡) = 𝑡 n·A·𝐶·𝑞𝑒 √𝐷0 19 √𝜋·𝑡 𝑄𝑑 (𝑡) = ∫0 𝑖𝑑 (𝑡 ′ )𝑑𝑡 ′ = 2n·A·𝐶·𝑞𝑒 √𝐷0 𝑡 √𝜋 20 In this equation, n represents the number of electrons involved in a single reaction between the ion and the electrode (unitless), A represents the electrode area, C represents the bulk concentration of the ions in the solution, 𝑞𝑒 is the charge of an electron, and 𝐷0 is the diffusion constant of the ionic species. When a potential is applied to an electrolytic cell, the net charge through the cell over time is useful for determining whether the charge through the cell is in fact limited by the diffusion of ions to the electrode. If it is, then the ions near the electrode surface will electrochemically react with the electrode surface, and the concentration of these ions near the 35 electrode surface will drop. Over time, this results in a concentration gradient of ions spreading from the electrode to the bulk solution over an increasingly greater distance. The Cottrell equation describes how the current, and consequently the net charge, through the electrochemical cell will drop as a function of time. If the net charge through the cell is proportional to time in some other manner, then the charge flow through the cell is limited by another process. Charge accumulating near the interface due to electrophoresis, for example, would not accumulate proportional to the square root of time. The total net charge through the cell when the potential is removed can also be used to measure how much charge was stored at the electrode/electrolyte solution interface, and can be compared with the net charge through the cell when the potential was applied to determine the leakage resistance of the electrolytic capacitor. For example, if 2 mC were measured to flow through the cell when a potential of 1 V was applied for 1 s, but only 1 mC was measured to flow from the cell when the electrodes were electrically connected, then one could estimate the leakage resistance to be approximately 1 kΩ. 3.3 Fabrication Techniques The diffraction grating cells assembled and tested in this thesis consisted of two electrodes, an unpatterned ITO film on glass and an ITO film on glass patterned into an interdigitated design. Creating the interdigitated design could have been done by using a mask to deposit the patterned ITO film directly on the glass; however, it was found to be easier to deposit a continuous layer of ITO film on the glass and then create the patterned surface by selectively removing the ITO where it was not needed. Two different approaches were used to remove these ITO films; photolithography and focused ion beam milling. 3.3.1 Photolithography Two different types of interdigitated electrodes were created for the experiments in this thesis. One had a diffraction grating pitch of 10 µm, and the second had a diffraction grating pitch of 800 nm. For the 10 µm diffraction grating pitch electrodes, photolithography was used to create the interdigitated design. This process involves the deposition of a thin layer of a lightsensitive material known as photoresist onto the ITO film. When exposed to ultraviolet light, this film chemically changes, allowing it to be removed with a solvent known as a developer. Selected areas of photoresist can be removed by exposing only specific areas of the photoresist 36 to ultraviolet (UV) light, which can be done using a material that transmits light in a predetermined pattern, known as a mask. Next, the exposed ITO film is removed with a chemical etchant, such as hydrochloric acid. Finally, the remaining photoresist is removed with a solvent known as the developer. The photolithography process to create diffraction gratings with electrodes separated by 10 µm was done by Applied Image, Inc. A commercial supplier was used because the process was a standard one done by this company, and so it was not necessary to develop the process ourselves. Further, it was decided it would be more reliable to have done by a supplier that does these types of procedures frequently. 3.3.2 Focused Ion Beam Milling The photolithographic process is fundamentally limited in the resolution it can achieve by diffraction effects of the light. The minimum possible resolution that can be achieved is on the order of the wavelength of light used, although the typical feature sizes that can reliably be created in practice are often much greater. Several suppliers capable of photolithography were consulted, but none were able to reliably create diffraction gratings with a pitch of less than 1 µm. For these reasons, a different process known as focused ion beam milling was used to create the 800 nm pitch diffraction gratings used in this work. Focused ion beam milling is capable of removing material by directing a focused beam of ions onto a surface. The ion beam ablates material by bombarding it with high energy ions that eject atoms from the material, a process known as sputtering. The advantage of removing material in this way is that it can be done extremely precisely. Spot sizes of less than 10 nm can be removed with careful ion beam milling46. This allows high resolution patterns. A combined focused-ion beam, scanning electron microscope (FIB-SEM) built by FEI Company, the Helios NanoLab 650, was used to do the patterning of the ITO films. The machine is located at the Centre for High-Throughput Phenogenomics in the Department of Dentistry at the University of British Columbia. Precise alignment between the focused ion beam and the SEM allows three dimensional imaging of materials. This can be done by using the focused ion-beam to first ablate a thin layer of the material, taking an SEM image, ablating slightly further into the material, taking another SEM image, and so on. 37 The FIB-SEM at UBC was used to mill ITO-coated glass electrodes into an interdigitated design with a sub-micron pitch. The ion beam diameter used for this milling was approximately 50 nm. The fabrication process posed some challenges because the size-scale of the grating (100 µm by 100 µm) was much larger than the typical size-scales used for focused ion beam milling. In addition, the precise patterning of the ITO film is not a process typically done using a focused ion beam machine. Nevertheless, it was determined that FIB milling was the most practical way to fabricate a sub-micron grating, and so a great deal of work was done to develop and perfect how the focused ion beam was controlled in order to achieve a good interdigitated pattern. The details of the operation of the machine are provided in Appendix A, and the details of the design of the ITO coated glass electrodes and the preparation of the ITO coated glass for focused ion beam milling are included in Chapter 7. 3.4 Analytical Techniques The radiant flux values of light as a fraction of the incident laser flux (the flux fraction) reflecting from the diffraction grating cells built and tested for the work in this thesis were compared to flux fraction values that were modeled using two different methods. This was done to determine whether the measured flux fraction values met expectations, and to help estimate some of the unknown experimental parameters of the system, such as the thickness of the layer of increased ionic concentration near the electrodes. Modelling was done in three steps. First, the flux fraction values were approximated using the Huygens-Fresnel principle to develop analytical equations (derived in Appendix B). Next, using these equations, the computational software program Mathematica was used to vary a few parameters (such as the ionic concentration of methylene blue near the electrodes) to provide a fit for the measured values that minimized the chi-square statistic. Lastly, using these fitted parameters, the system was modelled numerically using these fitted values to verify that the Huygens-Fresnel based calculations were valid. 3.4.1 Huygens-Fresnel Based Calculations The Huygens-Fresnel principle is a well-known principle that can be very useful in conditions where the results are accurate, although the validity of these calculations depends on the system being modeled. The accuracy of the results can be verified by checking the results 38 using other methods, such as the numerical approach used by GSolver. The advantage of using calculations based on the Huygens-Fresnel principle is the much faster speed at which the calculations can be done. A numerical program such as GSolver has extremely limited optimization routines. Determining the optimal parameters of a system using GSolver could take hours or days. Using the analytical results from the Huygens-Fresnel based calculations, however, allowed the use of powerful minimization algorithms in the computational software programs such as Mathematica. These minimizations could be done in a matter of seconds using the Huygens-Fresnel based calculations. The details of the Huygens-Fresnel principle and how the derivation for the equations used to model the diffraction peak flux fraction values can be found in Appendix B. The conditions of the system where the calculations were valid were not tested, but in every case where these calculations were used for the work in this thesis, they were verified using a numerical program, GSolver. 3.4.2 GSolver GSolver models diffraction peak flux fraction values by defining a single diffraction grating period consisting of a superstrate, the medium the incident light is striking the grating from, a substrate, the final material the light transmits into, and the intermediate materials inbetween the superstrate and substrate. Figure 3-4 depicts a grating period one might define in GSolver. The electric and magnetic fields (E and B fields, respectively) in the superstrate are first found by setting them be an inhomogeneous plane wave, i.e., the sum of the incident plane wave E and B fields, plus a sum of reflected E and B fields for each diffracted order. The E and B-fields in the substrate are set as the sum of the transmitted diffracted plane waves. Boundary conditions are then applied to each interface in the grating. The components of the E-field parallel to the material interfaces are set to be continuous. GSolver then applies Maxwell’s equations to these E and B fields, resulting in a set of coupled differential equations. These equations are then solved using numerical methods. 39 Diffraction Grating Period Superstrate Intermediate Materials Material Thickness Material Width Substrate Figure 3-4: Graphical depiction of a user-defined diffraction grating in GSolver. The diffraction grating depicted here consists of four materials: a superstrate (white), substrate (gray), and two intermediate materials with variable thicknesses and widths (shown in hashed gray and white). One notable limitation to a program such as GSolver is the time it takes to change certain parameters in the grating being modelled. Some parameters, such as the dimensions of the grating, can be varied quickly and easily while other parameters, such as the index of refraction of the materials, require the user to manually change the material property between each simulation. This can drastically increase processing time, and is the main reason it was used in combination with the Huygens-Fresnel based calculations. 3.4.3 Comparison of Results from Huygens-Fresnel Based Calculations and GSolver The Huygens-Fresnel based calculations and GSolver were both used to model the diffraction pattern of light reflecting from the diffraction grating. One example model of a diffraction grating is given here and the results from GSolver and the Huygens-Fresnel based calculations are given here. The grating modeled here was similar to the one depicted in Figure B-9. 650 nm s-polarized light was used as the incident light, incident on this grating at an angle of 65°. The materials had indices of refraction of 1.51, 1.93, 1.33, and 1.33 + 0.1i for n1, n2, n3, and n4 respectively (meant to represent glass, ITO, water, and water with methylene blue). The radiant flux values for four different diffraction peaks were modelled, the 1st, 2nd, 3rd, and 4th order diffraction peaks. The thickness of the ITO was chosen to be 25 nm. The thickness of the 40 MB/water layer was also chosen to be 25 nm. The diffraction period, d, was chosen to be 20 µm. The width of the ITO was varied from 0 µm to 10 µm in order to give many points for comparison. This variable was chosen to be varied as it was easily varied in the GSolver software. The same parameters were used and simulated in GSolver, which has results shown in blue. Dotted lines are used to connect data points, to help visualize outliers. Figure 3-5: Huygens-Fresnel results vs. GSolver results. GSolver results contained some outliers (some of these values too large to be shown in this graph)—likely resulting from some unknown numerical errors. From Figure 3-5, there are a few points where the results from the Huygens-Fresnel based calculations and the results from GSolver differed. These can be seen in the results for a width of the ITO electrodes of less than approximately 2.5 µm. The reason for the difference was not apparent, but these differences did not exist for the results used in this thesis. The processing time for the Huygens-Fresnel based calculations was almost immeasurably small, while the results from GSolver took several seconds to calculate. 41 In addition, in future devices with more complex systems, such as for a diffraction grating with many independently controlled electrodes, the faster and more readily modified calculations based on the Huygens-Fresnel principle could be useful for determining the optimal controlling scheme. In summary, the method for calculating the fractional diffraction peak radiant flux values based on the Huygens-Fresnel principle was in agreement with a diffraction grating solver program that solved for diffraction peaks using numerical methods. These Huygens-Fresnel based calculations were used in this thesis because they allowed for many options in modelling, including very quick and easy variable changes, and powerful optimization algorithms when combined with programs such as Mathematica. Such options were not nearly as practical with a program such as GSolver. These calculations may also be useful for designing complicated control schemes in future applications of this method for electro-optic diffraction. 42 Chapter 4: Interface of ITO and Methylene Blue in Water The electro-optic diffraction grating described in this thesis is formed from non-porous ITO films, and actuated using the electrophoresis of methylene blue ions dissolved in water. Preliminary experimentation (unpublished) had shown that the interface of ITO and methylene blue ions dissolved in water (referred to as the ITO/MB-H2O interface) may exhibit supercapacitance and make greater reflectance changes possible. In this chapter, an experiment is described that experimentally verified and quantified this supercapacitance and the degree of controllable light absorption of this interface. The experimental cell used for these experiments did not use films patterned into interdigitated electrodes, but rather used unpatterned ITO films in order to measure the basic interfacial behavior before introducing the complexity of a diffractive structure. The hypothesis was that the measured reflectance changes would be much greater than in previous work (~ 1% changes23) due to the supercapacitance of the ITO/MB-H2O interface. 4.1 Design Requirements An experimental cell was designed to measure the supercapacitance and the degree of controllable light reflectance of the ITO/MB-H2O interface. The cell consisted of two electrodes of ITO coated glass with an electrolyte solution of methylene blue dye dissolved in water sealed between them. A diagram of this cell, which will be referred to as a planar cell (since the electrode of interest is unpatterned), is shown in Figure 4-1(a). A photograph of a planar cell is shown in Figure 4-1(b). The primary constraints on the design of this cell were the relative size of the two ITO films in contact with the dye solution, and the distance between these electrodes. 43 Figure 4-1: Planar cell design. In (a), a schematic of the experimental cell is shown. In (b), a photo of an experimental cell is shown, with a laser beam reflecting from the working electrode interface. Two electrodes were used in this cell, but light reflects from only one of the electrodes (the top electrode depicted in Figure 4-1(a) and (b)). This electrode, referred to as the working electrode, had an area exposed to solution of 2 mm by 4 mm. The ITO film outside this active 44 electrode area was covered with a non-conductive sealant that would prevent it from being in contact with the electrolyte solution, ensuring it would not contribute to the capacitance. The sealant used for this purpose, an RTV silicone sealant, was chosen because it was impermeable to water, readily available, chemically inert, and could also be used to seal the cell, reducing the amount of materials used in the cell. The area of the bottom ITO coated glass electrode in contact with the methylene blue / water solution was chosen to be 50 times greater, with an area of 2 cm by 2 cm. When the electrolytic cell was charged by applying an electrical potential between the two electrodes, a portion of the ions in the solution in the cell were moved via electrophoresis near one of the electrodes. For simplicity, the cell was designed to have enough solution sealed within it such that this movement of ions would not substantially change the bulk concentration of ions. For example, if the effective capacitance of the ITO/MB-H2O interface were 100 F/m2 (an overestimate), then under application of a 1 V applied potential between the two electrodes, the 2 mm by 4 mm ITO film would attract as much as 5 x 1015 ions to the interface. The concentration of the solution of methylene blue dye in water was nearly saturated, at a concentration of 1.32 x 1026 ions/m3 (0.22 M). At this concentration, the volume required to have 100 times this many ions is 3.8 x 10-9 m3. The solution between the electrodes was sealed in an area that was 2 cm by 2 cm, so the distance between the electrodes needed to be at least 10 µm in order to have room for this volume of solution. In the actual experiment, this distance was chosen to be 2 mm because there was no disadvantage to the added distance, and the increased distance made experimental cells easier to fabricate, improved reproducibility, and simplified the injection of solution into the cell. The separation of the two electrodes was done using 2 mm diameter rubber tubing, which provided the spacing necessary and also created ports for fluid injection and removal. A prism was used to achieve the necessary angle, in glass, for the incident laser beam to reflect by means of total internal reflection from the ITO/MB-H2O interface. Without the prism, it would not be possible to achieve the angle in glass necessary to achieve total internal reflection at the ITO/MB-H2O interface. Further, any light reflecting by means of total internal reflection (TIR) from the ITO/MB-H2O interface would also reflect by TIR from the glass/air interface and so would not exit the glass. Using a prism changes the angle that the light strikes the air/glass interface so that it can achieve the necessary angle for TIR. After light reflects via TIR, the prism 45 face also changes the angle the light strikes the glass/air interface and allows this light to exit where it can be measured by the integrating sphere and photodetector. The prism was placed on this cell and Cargille non-drying immersion oil47 was placed between the cell and the experimental cell. This oil had an index of refraction nearly equal to that of the prism and the glass of the ITO/glass electrode, and because of this it was used to largely eliminate the Fresnel reflections between these two interfaces. 4.2 Experimental Set-Up The experimental set-up consisted of an apparatus for holding the planar cell, a laser and optical arrangement for focusing the laser light onto the ITO/MB-H2O interface, an apparatus for measuring the reflected light, and an apparatus for applying electrical potentials to the planar cell. The planar cell was placed on a Siskiyou Design Inc.’s MXT angular platform48. The angle of the platform was chosen so that the incident laser beam struck the ITO/MB-H2O interface at an angle of 63.5°. The critical angle between the glass and electrolyte solution was 61.7°. The uncertainty in the incoming angle was estimated to be 0.2°. There were no major drawbacks to being a few degrees greater than this angle, so 63.5° was chosen to ensure light would undergo total internal reflection at this interface. A 650 nm Melles Griot 3 mW laser was used as the light source. A 2 mm diameter aperture was placed in front of this laser beam to reduce the beam size and remove any uncollimated light emitted from the laser. A linear polarizer was aligned to transmit s-polarized light and placed in front of the aperture. The linear polarizer was used so that the polarization of the light incident on the interface would be known in order to simplify the modelling of the diffraction grating. S-polarization was chosen arbitrarily over p-polarization; there was no reason to believe polarization would make a difference in the results. Lastly, a 50 cm focal length lens was used to focus the laser beam onto approximately the center of the 2 mm by 4 mm ITO/MB-H2O interface. 50 cm was chosen as the focal length in order to focus the laser beam to a spot of diameter approximately 1 mm by 1 mm while minimizing the angular spread of the laser beam to approximately 0.1°. These experimental components are depicted in Figure 4-2. 46 Integrating sphere with photodetector 2 mm diameter aperture 50 cm focal length lens 650 nm laser 50 cm Linear polarizer – transmits s-polarized light Planar cell with prism Figure 4-2: Optical arrangement used for planar cell measurements. Incident laser light is focused onto the working electrode/solution interface. Reflected light from this interface is measured with a photodetector located in an integrating sphere. Measurements were performed using an integrating sphere, photodiode, and amplifier described in Section 3.2.1. The signal from the amplifier was recorded using a LabView program and data acquisition (DAQ) card. The potentials were applied to the electrochemical cell using a computer and the program LabView, the analog voltage output capability of the DAQ card, and an operational amplifier. A diagram of the circuit used for powering a programmed sequence of voltage values versus time, which is referred to throughout this thesis as an applied potential sequence, is depicted in Figure 4-3. The applied potential sequences were created using a computer program commonly used for experimental control, LabView49. A LabView program was written that created the designed potential sequence, and then these voltages were applied to the experimental cell using a data acquisition (DAQ) card and an operational amplifier (op-amp). The DAQ card of the computer was not designed to provide more than 5 mA of current, so to prevent any current limits from affecting experimental results, a 741 op-amp with unity gain was used (depicted in Figure 4-3). In this configuration, the potential sequence from the DAQ card is given a voltage gain of -1 by the operation amplifier. The benefit of this configuration is that the power source driving the applied potentials is the op-amp, which is capable of producing much more current than the DAQ card. 47 DC Input Voltage 5.54 kΩ Voltage to Planar Cell 741 Op-Amp 5.54 kΩ + 15 V 8Ω 99.6 kΩ - 15 V Figure 4-3: Circuit used for applying potentials to planar cell. An operational amplifier is used, calibrated to have a gain of -1 V and a DC offset of 0 V. Potentiometers were used to remove the offset voltage from the op-amp and to set the gain of the op-amp. One potentiometer was placed in series with a -15 V DC voltage source and a 99.6 kΩ resistor. This resistance was chosen to be sufficiently large that the potential across a potentiometer of order 10 Ω in series with ground would have a potential across it of order 1 mV, which was the estimated offset voltage of the op-amp. The potential applied to the op-amp was then electrically shorted to ground, and the voltage from the op-amp was measured to be +1.2 mV. The resistance of the potentiometer was then increased to 8 Ω until the voltage was measured to be 0 V +/- 100 µV. A second potentiometer was used to set the gain to -1.0000 +/- .0001. A fixed resistance of 5.54 kΩ was placed in series with the voltage input from the DAQ card, and a potentiometer was used as a variable resistor to connect the output terminal of the op-amp to the low terminal, as shown in Figure 4-3. The voltage at the output terminal of the op-amp was measured while a 1 V signal was applied by the DAQ card. The potentiometer resistance was then varied to 5.54 kΩ until the voltage was 1 V +/- 100 µV. 4.3 Fabrication Techniques The assembly of the planar cell was carried out in the following steps: 48 1. The ITO/glass electrodes were first cleaned by soaking in distilled water and wiping with AccuWipe task wipers. The electrodes were then immersed in a glass beaker containing distilled water, and the solution was placed in a Branson 200 ultrasonic cleaner, also filled with distilled water. The ultrasonic cleaner was then turned on for a period of five minutes. 2. MG Chemicals silver epoxy was used to create a robust electrical connection between the ITO layer and a wire lead that was later connected to the voltage source. The epoxy was then cured in an oven at 65°C for 20 minutes. 3. The ITO/glass electrode had the majority of its area covered with silicone sealant. A 2 mm by 4 mm rectangle was marked on the glass-side of this ITO/glass electrode. Using a stereo microscope, the silicone was applied using a cotton swab to coat the ITO everywhere except for the marked 2 mm by 4 mm area. The electrode was then set aside to cure for at least two hours. 4. A non-electrically conductive material, in this case small lengths of 2 mm diameter rubber tubing, were positioned between the two electrodes, at the four corners. Two of the tubing pieces were placed in such a way that they would allow for MB-H2O solution to be injected into or extracted out of the cell. The other two pieces were used only as spacers, to maintain a consistent separation distance between electrodes. The two ITO/glass electrodes were then sealed together using more silicone sealant. The cell was then left to cure overnight. 5. Lastly microscope immersion oil was placed between the prism and the ITO coated glass electrode. (The components described in the fabrication steps are shown in Figure 4-1.) 4.4 Experimental Results The effective capacitance of the interfaces of ITO and the methylene blue in water solution when methylene blue ions were attracted to the ITO (referred to as the ITO/MB-H2O interface) and when chlorine ions were attracted to the ITO (referred to as the ITO/Cl-H2O interface) were determined by applying both positive and negative potentials to the cell and monitoring the voltage across a 900 +/- 1 Ω resistor connected in series with the planar cell. The circuit diagram for the planar cell is depicted in Figure 4-4. The net charge through the cell during these time periods was then calculated, at any time, by dividing the voltage across the series resistor by the series resistance to determine the current, and then integrating this current 49 with respect to time. Constant potentials were applied for a period of four seconds, followed by an applied potential of 0 V (electrodes electrically connected to ground) for 96 seconds. Figure 4-4: Circuit diagram for planar cell Different potentials were applied to a planar cell, and the reflectance of the laser light off the ITO/MB-H2O interface was measured. Different periods of applied potentials were tried, but a period of 4 s was found to produce the largest reflectance changes of this interface. During these preliminary tests, the reflectance changes were observed to occur over the course of a few seconds, so a period more than ten times this amount, 96 s, was chosen as the time for which the electrodes would both be electrically connected to ground. During this time, the working electrode was electrically connected to ground via the series resistor, so the voltage through the series resistor could be used to calculate the total charge that dissipated from the capacitor. Some of the charge stored at the interfaces dissipated through the electrode resistance (depicted back in Figure 2-3), so this method of estimating the charge storage represents a lower limit of the effective capacitance. Figure 4-5 shows the current density through the cell, calculated by dividing the measured current by the working electrode area (current density allows easier comparisons between cells of different areas). In this case, +1 V was applied to the cell and so chlorine ions were attracted to the ITO working electrode. 50 Figure 4-5: Current density through planar cell when chlorine ions are attracted to the working electrode. Labels indicate the integrated current values for time periods when a 1 V potential difference was applied between electrodes, and when no potential difference was applied. Arrows indicate the relevant axes for each data set. Next, a -1 V potential was applied to the planar cell, which attracted methylene blue ions to the working electrode. The current density through the cell when -1 V potential was applied is shown in Figure 4-6. In this case, the current through the cell dropped significantly after the potential had been applied for approximately 2 s. The exact cause for this change was unknown, but is likely the result of unknown electrochemistry occurring at the ITO/MB-H2O interface. A more thorough analysis of the charge flow through a planar cell is described in Section 6.2 . 51 Figure 4-6: Current density through planar cell when methylene blue ions are attracted to the working electrode. Labels indicate integrated current values during time periods when a -1 V potential difference was applied between electrodes, and where no potential difference was applied. The currents shown in Figure 4-5 and Figure 4-6 were integrated during four characteristic time periods: when 1 V was applied (chlorine ions attracted to working electrode), afterwards when zero potential was applied, when -1 V was applied (methylene blue ions attracted to working electrode), and after this when zero potential was applied. The total charge per area of working electrode through the cell during these times, the integral of the measured currents, is shown in Table 1. These values depend strongly on the length of time the potential was applied, (in this case the potentials were applied for four seconds). As can be seen from these net charge flows, the effective capacitance was found to be highly dependent on the ionic species at the working electrode. When methylene blue ions were present, the effective capacitance was many times greater than when chlorine ions were present. This suggests very 52 different processes are taking place at the interface of ITO/MB-H2O and ITO/Cl-H2O, as will be discussed further in the results section. Table 4-1: Net charge per area of working electrode during four characteristic time periods Applied Potential (V) Charge Density (C/m2) Period 1 +1 V (Cl- to working electrode) 22.4 C/m2 Period 2 0V -3.6 C/m2 Period 3 -1 V (MB+ to working electrode) -51.8 C/m2 Period 4 0V 39.8 C/m2 An applied potential sequence consisting of potential pulses of increasing magnitude was applied to the cell to assess how the effective capacitance and the amount of light absorption depended on the applied potential. Potentials were applied in the same manner as described previously; potential pulses were applied for a period of four seconds, followed by 96 seconds of zero applied potential difference to allow the system to return to its initial state. For potential sequence, 100 potential pulses were each followed by 96 seconds where the electrodes were electrically connected via the series resistance. The first 50 pulses were of incrementally decreasing magnitude (from 0 V to -1 V), and the following 50 pulses were of incrementally increasing magnitude (-1 V to 0 V). The total applied potential sequence lasted over two hours. The applied potential sequence to the cell is shown in Figure 4-7. 53 Figure 4-7: Applied potential sequence to the planar cell. Inset shows a single potential pulse. The scaling of the inset has been altered for visualization purposes. The radiant flux of the reflected light from this interface was measured while this potential sequence was applied to the planar cell. The measured flux, normalized to the flux of the incident laser beam (referred to hereafter as the flux fraction), is shown in Figure 4-8. The measured flux fraction was measured to be initially 20% of the total light, but dropped to as low as 10% of the total light when potentials around -1 V were applied. The initial reflected flux fraction of 20% indicated that approximately 80% of the incident laser flux was being absorbed at the ITO/MB-H2O interface. This degree of absorption is discussed further in the following section, but is actually less than one would expect for the concentration of methylene blue monomer. This is likely due to the methylene blue being present in other forms, such as dimers or trimers of methylene blue, which is known to happen at the concentrations of methylene blue used here. An additional 10% of the laser light was absorbed when potentials of order -1 V were 54 applied, which is far greater than that observed with other ITO and other dyes dissolved in solvent. These types of systems often can reversibly absorb about 1% of the incident laser light. Figure 4-8: Measured reflected flux fraction from planar cell. Inset shows the flux fraction when the -1 V pulse was applied to the cell. The axes of the inset are not to scale. The total charge stored in the cell at different applied potentials was found by integrating the currents through the cell after periods of applied potentials (calculated based on the voltage across the series resistor as previously described). The amount of charge dissipated from the cell was found to vary significantly with the magnitude of the applied potential. These charges are shown in Figure 4-9. 55 Figure 4-9: Charge dissipated from planar cell after applied potentials were set to zero. Charge from the cell increased significantly above potentials of 0.6 V. A slight drop in charge dissipation was observed above 0.95 V. 4.5 Discussion The measured amount of charge stored at the interfaces when methylene blue ions and chlorine ions were attracted to the working electrode surface at applied potentials of -1 V and 1 V, respectively, were 3.6 C/m2 and 39.8 C/m2. The effective capacitance of these interfaces can be found by dividing this charge storage by the potential across these interfaces. Thus, the effective capacitances of these interfaces at an applied potential of -1 V and 1 V are 3.6 F/m2 and 39.8 F/m2 respectively. The effective capacitance of the ITO/MB-H2O interface at other applied potentials is shown in Figure 4-10. 56 Figure 4-10: Effective capacitance of the electrochemical cell – the charge dissipated from the cell when applied potentials were set to zero was divided by the applied potential. The effective capacitance of the ITO/MB-H2O interface was found to vary significantly with the applied potential. A capacitance that varies based on applied potential is common for capacitors that rely on electrochemical reactions, so this was consistent with a capacitor that stores charge by the reduction and deposition of charged particles on the ITO surface. Based on the concentration of methylene blue used in these experiments, the Debye length, using equation (2), can be estimated to be 1.1 nm in length. The corresponding capacitance one would estimate for this Debye length, based on equation (3), would then be about 1.1 F/m2. The measured capacitance for the ITO/Cl-H2O interface was roughly consistent with this model when one accounts for the fact that the ITO surface is not perfectly smooth, but has a roughness to it that effectively increases its area, so this interface was not necessarily supercapacitive. The effective capacitance of the ITO/MB-H2O interface, on the other hand, was found to be substantially larger. As was already discussed in Section 1.3, the effective 57 capacitance at this interface was too large to be due to charged particles held at the electrode surface, and so must be due to molecules that were neutral in charge. The effective capacitance of this interface was largely voltage-dependent, increasing substantially at a potential around -0.55 V. As was mentioned in Section 3.1, the reduction potential of methylene blue ions at an ITO electrode with respect to a Ag/AgCl/KCl reference electrode is -0.275 V. The experiments done for this thesis did not use reference electrodes such as these in the experimental cells, due to there not being an easy way to include these electrodes, and because the focus of these experiments was on the effects produced from these applied potentials rather than on understanding the electrochemical phenomena occurring. In a separate experiment, however, the potential of an ITO electrode with respect to a Ag/AgCl/KCl reference electrode was measured in a solution of 0.22 M MB dissolved in water (no potentials were applied in this experiment). The potential of the ITO electrode was measured to be at 0.205 V with respect to the Ag/AgCl/KCl reference electrode. For the experiments described in this section, the area of the large ITO/Cl-H2O interface was designed to be sufficiently large that the potential drop across this interface was negligibly small. Therefore, in the experimental configuration, one would predict the reduction of MB at the working electrode to begin to occur when a potential of around -0.480 V (-0.275 V - 0.205 V) was applied to the cell. This was approximately the applied potential at which the measured effective capacitance began to increase; suggesting that the reduction of methylene blue ions into leucomethylene blue could very well play a role in the measured effective capacitance. The amount of evanescent absorption at the ITO/MB-H2O interface was much larger than that achieved with interfaces of ITO and other dyes23. The absorption cross section of methylene blue monomer at 650 nm is 2.18 x 10-20 m2. Other forms of methylene blue absorb 650 nm light less strongly than the monomer, so to obtain a lower limit on the amount of ions needed to achieve this degree of light absorption, we estimated the amount of the monomer that would be required to achieve the observed light absorption. Based on equation (12), this worked out to a surface density of 3.18 x 1019 ions/m2; equivalent to a surface charge density of 5.10 C/m2. Considering that the greatest possible ionic density at the electrode surface is likely about that of methylene blue in its solid form (2.83 x 1027 ions/m3 (4.70 M)), this would require a compact layer of methylene blue ions at the electrode surface that was 11 nm thick (calculated by dividing 58 5.10 C/m2 by the density of solid methylene blue and the charge per ion). The electric field between a parallel plate capacitor, using equation (4), separated by an effective distance of 5.5 nm (half of the estimated 11 nm compact layer), with a charge on the electrodes of 5.10 C/m2, is 7.19 x 109 V/m assuming the electrical permittivity was that of water, which is a conservative assumption. (In this small region the permittivity could be less than that of water, and the corresponding field would then be higher.) The required applied voltage is the product of the field and the effective gap distance, which yields a conservative estimate of the required voltage of about 40 V. This is about two orders of magnitude greater than our observed voltage requirements, proving that average charge of the species concentrated in the light absorbing layer was nearly zero. As mentioned earlier, it is possible for the neutral form of methylene blue, leucomethylene blue, to be formed at the surface, but it generally has not been observed to absorb visible light, so other net-charge-neutral absorption mechanisms must be involved. The mechanism through which the effective capacitance and degree of reversible light absorption was achieved is still not completely understood, but it is discussed in more detail in Chapter 6. 4.6 Summary The effective capacitance of the ITO/MB-H2O interface was measured to be at least 39.8 F/m2, a capacitance too large to be possible through standard electrolytic capacitance. This effective capacitance was the result of a reversible chemical reaction, a characteristic of a supercapacitor. The corresponding magnitude of reflectance of this interface was measured to drop by a factor of two, much larger than has been achieved with other dyes in similar experiments. This indicates that the charge-storage mechanism operating here could be useful in an electro-optic diffraction grating. The next step in this work was to experimentally verify that this interface could be used to make an electro-optic diffraction grating. 59 Chapter 5: Electro-Optic Diffraction Grating Cell The experimental results reviewed in Chapter 4 showed that the ITO/MB-H2O interface exhibited supercapacitance, and was capable of reversibly reducing the light reflecting from this interface by 50%. These results indicated that this interface could be useful for an electro-optic diffraction grating, so the next experiment was designed to build and test an experimental cell capable of electro-optic diffraction. This cell has a design similar to that for the planar cell, but in this case the working electrode was patterned into two interdigitated electrodes (and so it will be referred to as a diffraction grating cell). The hypothesis was that a potential applied between these interdigitated electrodes would change the reflectance of one of the electrodes. This would cause light reflecting from this interface to interact with a diffraction grating that had an associated grating pitch of twice the spacing between adjacent electrodes, resulting in a new diffraction peak. Based on the reflectance changes measured in the previous chapter from a planar cell, the newly created diffraction peak was expected to have a flux fraction that reversibly modulated about 1% of the incident light. 5.1 Design Requirements The design constraints for this cell were similar to that of the constraints for the planar cell. The main differences between the planar cell and these diffraction grating cells were related to the patterning of one of the electrodes. The diffraction grating cells consisted of three electrodes; two interleaved ITO films on one side of the cell, and a planar counter electrode on the other side. Three electrodes were used to compensate for the vastly different capacitances of the ITO/MB-H2O and ITO/Cl-H2O interfaces. Because the interfaces are capacitors in series, the amount of charge stored at one interface must be equal and opposite to the charge stored at the other interface. If only two interdigitated electrodes were used that were equal in area, then the potential drop across the ITO/Cl-H2O interface would be much greater since the capacitance of this interface is much smaller (this is explained in more detail in Section 3.2.3). One potential way around this limitation would be to make one of the interdigitated electrodes much larger in area than the other, but this way introduces an asymmetry that could lead to a permanent, irreversible diffraction peak. Instead, electrodes of equal area were used so it would be possible to provide equivalent electrical treatments to both of the electrodes, which 60 helped to ensure that there would be no irreversible diffraction peak created (described in more detail later in this section). Another way to compensate for the differences in capacitances was simply to use a third electrode, a counter-electrode, with a much greater area than either of the interdigitated electrodes. This counter-electrode was always maintained at earth ground. The three electrode design was the one used for the diffraction grating cells described in this chapter, depicted in Figure 5-1. The two interleaved electrodes consisted of an ITO film on glass patterned into an interdigitated design. The counter-electrode consisted of one unpatterned ITO film on glass. Wire Silver epoxy 1 mm diameter spacer beads Prism ~ ~ 2.5 cm Silicone 10 µm Methylene blue in H2O Interdigitated ITO pattern created using photolithography Figure 5-1: Electro-optic diffraction grating cell The dimensions of the interdigitated electrodes are shown in Figure 5-2. The distance between the digits of the ITO films was selected to be as small as could reliably be created via photolithography, which was 10 µm. The width of these digits was set to be about 6.5 µm. The area of the interdigitated electrodes, an area 2 mm by 4 mm in size, was selected to be only large enough to enable a laser beam to be easily focused onto the grating, but no larger, in order to reduce the probability of a defect in the photolithography process causing an electrical connection between electrodes. The area of the counter-electrode in the diffraction grating cell 61 was chosen to be 2 cm by 2 cm, in order that its area would be more than 100 times greater than that of either of the interdigitated electrodes. Figure 5-2: Dimensions of diffraction grating The distance between the electrodes was set by placing 1 mm spacer beads in between the ITO coated glass electrodes. This spacing was chosen to ensure the bulk concentration of methylene blue ions did not change significantly when a portion of the methylene blue ions were attracted to any of the electrodes in response to an applied potential. For simplicity in the description, the potentials applied to the interdigitated electrodes will be referred to with respect to the grounded counter-electrode. Two inverting op-amps in series were used to insure the potentials applied to each of the interdigitated electrodes were always equal and opposite to one another. A diagram of the circuit used to apply potentials to these electrodes can be seen in Figure 5-3. Two 900 Ω resistors were placed in series, and the voltage across these resistors was measured and recorded to determine the currents to each of the electrodes. 62 Figure 5-3: Circuit schematic for 10 µm diffraction grating cell electrodes. An operational amplifier was used to enable the production or large currents. A second inverting operational amplifier was used to produce a second equal and opposite applied potential sequence. 5.2 Experimental Set-Up The optical arrangement used to measure the diffraction pattern from this cell was nearly the same arrangement used for the planar cell, and is shown and explained in the previous chapter, depicted in Figure 4-2. One change to the experimental setup was the addition of three adjustable platforms to aid in the alignment of the incident laser beam on the interdigitated electrode area of the diffraction grating cell. One of these platforms was movable in three axes, referred to as an xyz platform, and this platform held the angular adjustment device on which the cell was mounted. The xyz platform was used for fine adjustments of the experimental cell. The xyz platform was placed on top of two additional platforms that were movable in only one direction, referred to as z-axis platforms (these are shown in Figure 5-4). The z-axis platforms were added so that one of these platforms could be adjusted to slightly angle the experimental cell. In terms of spherical coordinates, the normal vector of the diffraction grating area had its polar and azimuthal angles aligned by altering the angle of the angle platform and the height of one of the z-axis stages, respectively. 63 Figure 5-4: Alignment components for diffraction grating cell The cell was aligned with the incident laser beam by first calculating the location of diffraction peaks reflecting from the cell assuming perfect alignment, and then iteratively repeating the alignment steps until the location of the reflecting diffraction peaks from the grating aligned within 0.1° from the calculated locations. In order to accurately align the grating, first the angles of the initial diffracted beams were calculated. A white diffuse board was placed on the wall behind the experimental cell, approximately 70 cm away. The precise locations where the diffraction peaks should strike this white surface were calculated and marked on the surface. The alignment procedure outlined below was then performed until all diffraction peaks from the cell struck these calculated marks to within 0.1°. The order of alignment steps, as well as the components and how they were moved/rotated for alignment are depicted in Figure 5-4. The alignment procedure was a multistep iterative process. The alignment steps below were carried out and repeated iteratively until diffracton peaks struck the calculated marks to within 0.1°. The order of alignment steps was the following: 1. Prism orientation - the front prism face was aligned orthoganol to the incident laser beam. This was done by adjusting the prism by hand until the slight reflection from 64 the incident beam off the front face was directed backwards, directly over the indicent beam. 2. xyz platform position – the xyz platform was adjusted until the laser beam was striking the diffraction grating. The platform was adjusted to maximize the apparent flux of the diffraction pattern, initially judged by eye, but in the final steps this was done using the integrating sphere/photodiode system described in Section 3.2.1. 3. Angular platform – the angle of the cell relative to the incident laser beam was adjusted using the anglular platform until the 0th order beam was striking the proper height on the white diffuse board. 4. Cell tilt – At this point, if the 0th order beam were at the proper height, but was off laterally, then it meant the cell was tilted with respect to the table plane. Two z-axis platforms were used to correct for this tilt. The height of one of these platforms were adjusted until the 0th order was striking the proper location. 5. Planar cell – Lastly, with the laser beam striking the grating area, and at the proper angle, the last thing to align were the interdigitated electrodes with the incident beam. When these electrodes were not aligned with the incident laser beam, the diffraction peaks were observed to be either above or below their predicted locations. The diffraction grating cell had to be adjusted on the xyz platform until these peaks were striking their proper location. Finally, all steps were repeated until no further adjustments were required and the diffraction peaks were all striking the predicted locations, to within 0.1°. The prism on the diffraction grating cell was not held onto the cell by any mounting fixtures, so to ensure the alignment of the cell was stable, the cell was left overnight. Alignment was checked the next day to ensure the alignment had been maintained before any experimental measurements were made. Light that reflected by means of total internal reflection from the interdigitated electrodes diffracted with a pitch equal to the digit spacing. A gray-scale photograph of the diffraction pattern of laser light reflecting from these interdigitated electodes after the completion of the alignment steps is shown in Figure 5-5. 65 Figure 5-5: Gray-scale photograph of diffraction peaks reflected from diffraction grating cell 5.3 Fabrication Techniques The assembly of the diffraction grating cell was similar to that of the planar cells from the previous chapter. It was done in the following steps: 1. The ITO coated glass electrode was patterned into an interdigitated design via standard photolithography. The photolithography was done by Applied Image, Inc. 2. The ITO coated glass electrodes were cleaned using first ethanol and then distilled water in a Branson 200 ultrasonic cleaner. Electrodes were immersed in a glass beaker containing the solution, placed inside the ultrasonic cleaner filled with distilled water, and treated for five minutes. 3. MG Chemicals silver epoxy was used to create robust electrical connections between wires and the ITO film. The epoxy was placed on the ITO film, and a wire was placed in the epoxy. The epoxy was then placed in an oven and cured at 65°C for 20 minutes. 4. The ITO coated glass electrode with the interdigitated pattern was insulated from solution using RTV Silicone Sealant. All the ITO film in the cell was covered with silicone, aside from the area comprised of the interdigitated electrodes. This process was done by hand, using a cotton swab and with the aid of a stereomicroscope. A collimated white light source was aimed at the ITO coated glass electrode, and the electrode was viewed under the microscope at an angle at which a diffraction peak entered the viewing lens. This made the diffraction area appear to be colored under the microscope, and greatly eased the application of silicone. 66 5. This electrode was then combined with a non-patterned ITO electrode, and made into a cell in the same manner described for the planar cell. For this cell, 1 mm diameter spacer beads were used to keep the two electrodes electrically-isolated. Silicone was used to seal the cell, and the silicone was left to cure overnight. Solution was then injected into the cell through the silicone seal using a syringe. 6. Lastly, microscope oil was placed on the glass-side of the ITO/glass electrode with silicone. A right-angle prism was placed on the oil. The oil acted as an indexmatching fluid between the glass of the prism and glass of the ITO/glass electrode, removing unwanted reflections between the prism and the ITO electrode surfaces. 5.4 Results After alignment, the initial diffraction peak flux fraction values were measured and recorded using the integrating sphere/photodiode system. A solution of 1.3 x 1026 ions/m3 (0.22 M) was injected into the cell through the silicone via a syringe. Once the solution was injected, the diffraction peak flux fraction values were again measured and recorded (zero potential applied to the electrodes). These measured values were found to gradually decrease by about 5% over a roughly 24 hour period before stabilizing. This could be due to methylene blue ions, or other ions, adsorbing onto the ITO surface. However, the experiments described in this section were performed on a cell that had been injected with methyelene blue solution for less than one hour, so only those measurements are reported here, summarized in Table 5-1. These measured flux fraction values were later modelled using a Huygens-Fresnel based calculation and GSolver (both described in Section 3.4). The diffraction grating cells were first tested by applying a 1 V potential pulse for 12.5 s (with respect to the grounded counter-electrode) to one of the interdigitated electrodes, and a -1 V potential pulse to the other electrode. The 1st order diffraction peak of the new diffraction pattern was then measured. This diffraction peak will henceforth be referred to as the interstitial order diffraction peak because it lies between the pre-existing peaks of the underlying grating (and sometimes referred to simply as the newly created diffraction peak). It will not be again referred to as a 1st order peak in order to avoid confusion with the 1st order peak of the underlying grating. 67 Table 5-1: Diffraction peak flux fraction values (ratio of measured flux to incident laser flux) Order Empty cell flux fraction Cell filled with MB-H2O flux fraction 0th 0.960 +/- 0.001 0.201 +/- 0.007 1st (1.51 +/- 0.09) x 10-2 (6.9 +/- 0.3) x 10-3 2nd (3.3 +/- 0.2) x 10-3 (1.6 +/- 0.2) x 10-3 3rd (5 +/- 3) x 10-5 (2 +/- 3) x 10-5 4th (9 +/- 1) x 10-4 (5.5 +/- 0.3) x 10-4 5th (3.5 +/- 0.4) x 10-4 (2.6 +/- 0.6) x 10-4 Figure 5-6 shows the measured flux fraction values of the interstitial diffraction peak from the cell while a series of potential pulses were applied. For ease of viewing, only the potentials applied to one of the interdigitated electrodes are shown. Figure 5-6: Interstitial diffraction peak flux fraction values. The measured diffraction peak was located at an angle of 1.9° +/- 0.1° with respect to the 0th order beam. Arrows indicate relevant axis for each data set. 68 These results demonstrated reversible electro-optic diffraction, at a flux fraction nearly identical to the 1st order diffraction peak of the underlying grating (0.8%). These flux fraction values had a minimum fraction value between applied potential pulses that gradually increased with each pulse. This appears as a permanent interstitial order, which remained even when the cell was left with zero applied potential overnight, implying that there was an irreversible change to one of the two interdigitated electrodes. There was also an asymmetry in the response of the two electrodes, shown in Figure 5-6 by the fact that the maximum measured diffraction peak flux fraction differed significantly depending on which interdigitated electrode received a given applied potential. This asymmetry grew even greater with each applied potential pulse. One possible explanation for this asymmetry could be that the response of the electrodes depended on whether it first received an applied potential that attracted methylene blue ions or chlorine ions. To test this hypothesis, a sequence of applied potentials was designed to mitigate this effect, by ensuring that the potential pulses applied to each electrode were slowly increased, while alternating between attracting methylene blue and chlorine ions. This potential sequence consisted of alternating positive and negative applied potential pulses of gradually increasing magnitude, separated by periods of no applied potential. The potentials applied to the two interdigitated electrode were always equal and opposite. The potential pulses were applied for 1 second, and then removed for 79 seconds to allow the system to return to its initial state. The potential sequence was symmetric, with the magnitude of the applied potential pulses increasing from 0 V to 1 V in 40 mV increments, and then back down to 0 V in 40 mV increments. The applied potential sequence to one of the two electrodes is shown in Figure 5-7. 69 Figure 5-7: Applied potential sequence to one of two diffraction grating electrodes The potential sequences were applied to the two electrodes in the diffraction grating and the resulting radiant flux fraction of the interstitial order peak was measured by the integrating 70 sphere, photodiode, amplifier system. The resulting flux fractions are shown in Figure 5-8. The measured flux values no longer showed a permanent increase in the reflected flux fraction over time, indicating the applied potential sequence was successful in mitigating this problem. Figure 5-8: Measured interstitial diffraction peak flux fraction. Measured diffraction peak was located at an angle of 1.9° with respect to the 0th order beam. Further applied potential sequences displayed decreasing performance. After one or two of these potential sequence applications to the cell, the flux fractions of the newly created diffraction peak became almost immeasurably small, indicating the experimental cell was no long functioning. However, for these experiments, our goal was to determine whether this system could be used for electro-optic diffraction, not to demonstrate longevity, so we did not attempt to increase the lifetime of the cell. 71 5.5 Comparison of Experimental Results with Model Predictions The flux fractions measured from the diffraction grating were calculated based on the Huygens-Fresnel principle (explained in more detail in Section 3.4) for three different cases. The first case was the diffraction peak flux fractions from an empty cell in order to use a least-squares fitting to determine the width and thickness of the ITO film electrodes. The second case was when the cell was filled with MB-H2O solution, but no potential was applied. The measured flux fractions of the diffraction peaks from these cells were fit to determine the imaginary component of the index of refraction of the MB-H2O solution. The final case, using the fit values from the first two cases, calculated the flux fraction of the newly created diffraction peaks. The results of these fits were used to determine how much dye was required to obtain the measured peaks, and to provide an estimate for the thickness of the increased concentration of dye next to the electrodes. These three cases are described in more detail below. The first case modelled the flux fraction of the diffraction peaks for an empty diffraction grating cell. In this case, no light was absorbed at the diffraction grating interface, so this was used as the reference light flux. These diffraction peak flux fractions were also used to infer two parameters of the grating by minimizing the chi-square statistic between the calculated and the measured flux fraction values. A depiction of the model of the grating used for analytical calculations is shown in Figure 5-9. The flux fractions measured when the device was empty, along with the fitted flux fractions, are shown in Table 5-2. The width and thickness of the ITO electrodes were used as free parameters for this fit. These parameters were fit by subtracting the fitted values by the measured values, dividing by the experimental uncertainty, and squaring this value for each diffraction order. These values were then summed to determine the chi-square statistic for the fit, and then the free parameters were adjusted until the chi-square statistic was minimized. The experimental uncertainty for each measured values was determined based on measurements from five different diffraction grating cells that were constructed. The diffraction peaks from these five cells were measured and compared. The variance in the measured reflected flux fractions of these cells for each diffraction order were used to determine the uncertainty in the measured values. 72 10 µm Glass n=1.51 ITO Thickness ITO n=1.93 ITO Width Air n=1.00 Figure 5-9: Graphical depiction of model of diffraction grating when experimental cell was empty. Table 5-2: Diffraction peak flux fraction for empty cell (ratio of measured flux to incident laser flux) Order Measured Flux Fraction Calculated Flux Fraction Δ % Difference 0th 0.960 +/- 0.001 0.961 0.001 0.1% 1st (1.51 +/- 0.09) x 10-2 1.51 x 10-2 0.00 x 10-2 0% 2nd (3.3 +/- 0.2) x 10-3 2.8 x 10-3 5.0 x 10-4 15% 3rd (5 +/- 3) x 10-5 1.1 x 10-4 6 x 10-5 120% 4th (9.0 +/- 1.0) x 10-4 1.0 x 10-3 1.0 x 10-4 11% 5th (3.5 +/- 0.4) x 10-4 2.4 x 10-4 1.1 x 10-4 31% These values are depicted graphically in Figure 5-10: 73 Figure 5-10: Diffraction peak flux fractions for empty cell The chi-square statistic was found to be minimized when the ITO film electrodes were chosen to be 6.5 µm in width, and 13.6 nm in thickness. The 6.5 µm width was expected as it was the width requested from the supplier. The sheet resistance of ITO used by the supplier was 100 Ω/square, which a similar supplier estimates to have an ITO film thickness of between 15 – 30 nm. The thickness of the ITO film estimated by the fitting was 13.6 nm. The chi-square statistic obtained for the fit of the diffraction peak flux fraction was 19.8, which corresponds to a p-value of only 0.003. Statistically, there was not good agreement between the model and reality. One explanation for this is that the model was incomplete, which is not surprising as this relatively simple model does not account for many things influencing the reflected flux fraction, such as the surface roughness or imperfections of the glass or ITO film. Nevertheless, the fitted values gave reasonable results that indicate this model provides a good starting point for modelling this system. The second case modelled the diffraction peak flux fractions when the diffraction grating was filled with 1.3 x 1026 ions/m3 (0.22 M) MB-H2O solution, but no potentials were applied. In this case, the imaginary component of the index of refraction of the MB-H2O solution (labelled 74 ĸ1 in Figure 5-11) was used as the only free parameter in the fitting. The setup for this model is shown in Figure 5-11. 10 µm Glass n=1.51 ITO 13.6 nm n=1.93 6.5 µm H2O with dissolved MB n=1.33 +κ1· i Figure 5-11: Graphical depiction of diffraction grating when experimental cell was filled with MB-H2O solution. Once again, the measured diffraction peak flux fractions were fitted by minimizing the chi-square statistic between the measured and calculated values. For this model, the chi-square statistic was minimized by altering the imaginary component of the index of refraction of the MB-H2O solution. The results of this fit are shown in Table 5-3 along with the measured flux fractions. Table 5-3: Flux fractions for cell with MB-H2O (ratio of measured flux to incident laser flux) Order Measured Flux Fraction Calculated Flux Fraction Δ % Difference 0th 0.201 +/- 0.007 0.182 0.019 9% 1st (6.9 +/- 0.3) x 10-3 8.2 x 10-3 1.3 x 10-3 19% 2nd (1.6 +/- 0.2) x 10-3 1.6 x 10-3 0.0 x 10-3 0% 3rd (2 +/- 3) x 10-5 6 x 10-5 4 x 10-5 200% 4th (5.5 +/- 0.3) x 10-4 6.0 x 10-4 5 x 10-5 9% 5th (2.6 +/- 0.6) x 10-4 1.6 x 10-4 1.0 x 10-4 38% 75 These values are depicted graphically in Figure 5-12. Figure 5-12: Normalized diffraction peak flux fraction values for cell filled with MB-H2O (no potentials applied to cell) The chi-square statistic was found to be minimized when the imaginary component of the index of refraction was 0.103. This value, using equation (16) and the absorption cross section of methylene blue of 2.396 x 10-20 m2, corresponds to an ionic concentration of methylene blue of 8.31 x 1025 ions/m3 (0.139 M). The actual concentration of methylene blue used for these experiments was 1.317 x 1026 ions/m3 (0.220 M). The differences in these values are likely due to the linking of methylene blue ions into dimers and trimers of methylene blue, which is known to happen at these concentrations. The chi-squared statistic value for this model was 30.7, which corresponds to a p-value of 3 x 10-5. This relatively small p-value once again indicates the model is not statistically in agreement with experiment, although once again this could be due to the model not being complete. This model was similar to the previous model, but it also had the added complexity of the methylene blue in water solution. An example of how this could add complexity to the model would be the adsorption of some methylene blue ions onto the ITO 76 surface (which has been observed to happen with different forms of methylene blue, especially forms such as trimer methylene blue50 and leucomethylene blue51). An adsorbed layer such as this was not accounted for in the model, and so would make a statistically significant fit nearly impossible. Nevertheless, the model once again gave reasonable results that provide a basic picture of how the measured diffraction peaks arise from light reflecting from this system. The final case modeled the diffraction grating when a potential difference was applied between the interdigitated ITO electrodes. In this model, a second film was added to the model around one of the two interdigitated electrodes. For this fit, the maximum measured flux fraction of 0.7% (the largest measured value in Figure 5-8) was modelled. The thickness and imaginary component of the index of refraction of this layer were used as free parameters for this fit. A diagram of the model for this case is shown in Figure 5-13. 20 µm Glass n=1.51 ITO n=1.93 13.6 nm n=1.33 + κ2· i MB Thickness 6.5 µm H2O with dissolved MB n=1.33 + 0.103· i Figure 5-13: Graphical depiction of diffraction grating when an applied potential of -1 V was applied to the interdigitated electrodes of an experimental cell. There was a range of imaginary index and layer thickness values that could be used in the model to match the measured interstitial diffraction peak flux fraction. The layer thicknesses ranged from 10 nm to as much as 150 nm. The imaginary component of the complex index for these layers ranged from 0.25 to 1.14. The fits with thinner layer thicknesses also had larger 77 imaginary components of the index of refraction, and vice versa, so the amount of ions needed to create these layers (or the amount of charge needed) was approximately constant. The number of ions needed to create these layers was found by using the absorption cross section for methylene blue monomer as a starting point, and determining the necessary ionic concentration required to achieve the imaginary component of the index of refraction using equation (16). The number of ions per area of electrode was then found by multiplying this number by the layer thickness. The amount of charge required to create these layers of increased methylene blue monomer concentration ranged from 2 to 6 C/m2. A more realistic estimate would be to estimate the amount of charge required to create such a layer consisting of leucomethylene blue molecules. To reduce and deposit leucomethylene blue to the ITO surface would require two electrons per methylene blue ion, and so would require twice as much charge, 4 to 12 C/m2, to deposit the same number of molecules. As already discussed, leucomethylene blue is not known to absorb visible light, and so the mechanism for the light absorption at the ITO interface was not known, but the amount of charge estimated at this interface was roughly consistent with the measured charge storage at this interface from Chapter 4. The maximum layer thickness estimate was also an important result, as it indicated that this method is in fact scalable to submicron size-scales, allowing for light deflection to larger angles than other methods. The minimum thickness estimate from these fits was also consistent with the estimated minimum thickness of molecules on the ITO surface estimated in the previous chapter (about 11 nm). The model also found that the total amount of light from the cell decreased, although the total flux fraction of diffracted light remained approximately constant, which is consistent with increased absorption at one of the interdigitated electrodes. 5.6 Summary Electrically-controlled diffraction was achieved using an experimental cell consisting of two electrolytic capacitors. These capacitors consisted of ITO films on glass plates submerged in a solution of methylene blue dye ions dissolved in water. Electro-optic diffraction was achieved by moving dye ions, by means of electrophoresis, into and out of the evanescent regions surrounding one of the two interdigitated ITO films. The local density of dye around the film was increased, creating a diffraction pattern associated with twice the spacing between electrodes. The flux fraction of one of these newly created diffraction peaks was measured at an 78 angle of 1.9° +/- 0.1° with respect to the 0th order beam, and was measured to reversibly modulate by the incident laser light by 0.7%. Modelling of the measured flux fractions indicated the amount of charge of methylene blue dye ions needed to create this measured flux fraction was between 4 and 12 C/m2. The thickness of the layer of these dye ions next to the electrode was estimated to be between 10 nm and 150 nm thick, indicating this system could be significantly reduced in size-scale, potentially to scales where the entire diffraction peak could be reversibly modulated. The mechanism through which the dye ions were controlled was not solely due to normal double-layer capacitance, so further study of the electrochemical phenomena taking place at the ITO/MB-H2O interface was warranted. A preliminary analysis has been carried out and is described in Chapter 6. Since the thickness of the layer of ions attracted to one of the two interdigitated electrodes was estimated to be no more than 150 nm, the system would work even if the pitch of the diffraction grating were reduced to a size on the order of a wavelength of light. At this sizescale there would be no initial diffraction, but a diffraction pattern could be created when a potential was applied between the interdigitated electrodes. Such a diffraction grating cell is described in Chapter 7. 79 Chapter 6: ITO/MB-H2O Interface Analysis Using Electrochemical Methods Supercapacitance of the ITO/MB-H2O interface and the resulting large degree of evanescent absorption shown in the previous chapters has never before been observed. The electrochemical phenomena giving rise to this supercapacitance and consequent light absorption was unknown, so two experiments were performed to elucidate the phenomena involved. These two experiments were performed to characterize the interface via two electrochemical methods: spectroelectrochemistry and double potential step chronocoulometry. Thorough spectroelectrochemistry and chronocoulometry tests were outside the scope of this project, but initial tests helped develop a rudimentary picture of the types of phenomena taking place at the ITO/MB-H2O interface, which can eventually be used to guide further research. 6.1 Spectroelectrochemistry The first method used was in situ spectroelectrochemistry, which was performed with the goal of determining the chemical species present at the ITO/MB-H2O interface. The spectroelectrochemistry was performed on a planar cell, and a collimated white light source was used as the incident light beam and directed at the cell in such a way that the light reflected by means of total internal reflection off the ITO/MB-H2O interface. An integrating sphere was used to collect and homogenize the reflected light, and a fiber optic cable connected to a port in the integrating sphere was used to transmit a portion of the light in the integrating sphere to a spectrometer. The light measured by the spectrometer was used to determine the absorption spectrum of the ions near the ITO/MB-H2O interface. Different potentials were then applied to the cell and the process was repeated to determine the absorption spectrum of the solution at different applied potentials. These absorption spectra were then compared to known absorption spectra of the different chemical structures of methylene blue in an effort to identify the chemical species present at the interface of ITO/MB-H2O interface. 6.1.1 Experimental Design The planar cells used in the experiments described in this section were altered from those described in Chapter 4 to allow the use of a collimated white light source, which was created by masking the light from a halogen light bulb with a series of apertures, as described in more detail later in this section. The resulting collimated beam measured approximately 2 mm by 4 mm in 80 area upon striking the ITO/MB-H2O interface. To accommodate this beam size, the working electrode area in contact with the solution was increased to 1.0 x 10-4 m2 (1 cm by 1 cm) to provide ample area for the incident white light beam. This increase in area, relative to previous cells, meant that a larger area counter-electrode would need to be approximately 5.0 x 10-3 m2 (50 cm2) in area, an area that was impractical to achieve with prior planar cell designs. Instead of a larger-area ITO counter-electrode, a sheet of highly porous carbon material, known as carbon nanofoam, obtained from Marketech International Inc.52, was used as the counter-electrode. The carbon nanofoam had a capacitance per unit area of material of 3000 F/m2. The area of carbon nanofoam in contact with the electrolyte solution was 2 cm by 2 cm, with a thickness of 250 µm, giving a relative capacitance more than 200 times greater than the ITO/MB-H2O interface. Incident white light Wire 3 mm diameter spacer beads Silver epoxy ~ ~ Prism Silicone Methylene blue in H 2O Carbon nanofoam on ITO on glass Figure 6-1: Planar cell used for spectroscopic measurements. The working electrode area in contact with solution was 1 cm by 1 cm. A sheet of carbon nanofoam is used as the large-capacitance counter-electrode. The planar cell used 3 mm spacer beads to separate the two electrodes. These spacer beads were placed in the cell to ensure the total volume between the electrodes was large enough that, when filled with MB-H2O solution, there would be sufficient solution contained in the cell to prevent any change in the bulk concentration when ions were attracted to the ITO surface. The 81 carbon nanofoam was adhered to an ITO coated glass electrode using conductive silver epoxy. ITO coated glass was used for this purpose only because it was readily available, and the electrode was of a convenient size (no transparency was needed for this electrode). The carbon nanofoam was adhered to the ITO coated glass electrode using conductive silver epoxy. The optical arrangement used for these measurements is depicted in Figure 6-2. The light source was a World Precision Instruments NovaFlex fiber optic illuminator53. The illuminator consisted of a halogen light bulb source, with a flexible fiber optic cable used to direct the light from the halogen bulb. Light from this flexible fiber optic cable was passed through two apertures to reduce the angular spread of white light incident on the cell. The first aperture was placed 25 mm in front of the fiber optic cable, and had an aperture diameter of 1 mm. The second aperture was placed 10.1 cm from the light source, and also had an aperture diameter size of 1 mm. This ensured that light striking the planar cell had an angular spread of no more than 1.5°. The small angle of 1.5° was chosen in order that the white light beam was similar to a collimated laser beam, while allowing sufficient transmission of light from the halogen light source to obtain measurements with a signal-to-noise ratio of greater than 10. The measurement system used for this experiment was an Ocean Optics integrating sphere with fiber optic cable connected to a spectrometer, described in more detail in Section 3.2.1. The cell was then placed on the same angular platform used for the planar cell experiments. The angle of the angular platform was set such that the white light was incident on the cell at an angle of 65°, with an angular spread of approximately +/- 1°. Potentials were applied to the planar cell in the same manner as was described in Chapter 4. Potential pulses were applied for a period of 4 s in total. The Ocean Optics SpectraSuite® spectrometer operating software54 was used to acquire and process the data from the spectrometer. The software integrated the signal from the spectrometer for a period of 0.1 s. Spectra were sampled after the potential had been applied for 3 s. Sampling was triggered by the user in the SpectraSuite® software, so sampling was done after 3 s to ensure the sampling occurred while the potential pulse was still being applied. 82 Integrating sphere Fiber optic cable 25 mm 76 mm 76 mm Halogen light source 5 mm aperture Spectrometer Fiber optic cable 1 mm apertures Figure 6-2: Optical arrangement used for spectroscopic measurements 6.1.2 Results The reflectance spectrum of an empty planar cell was measured, averaged over 1 s, to determine the spectrum of light reflecting from the cell in the absence of any absorption at the interface. 6 x 1025 ions/m3 (0.1 M) methylene blue solution was then injected into the cell, and another reflectance spectrum was taken. Using equation (12), described in Section 2.8, the natural logarithm of the ratio between these two spectra was then used to determine the absorption coefficients (the absorption cross section multiplied by the ion concentration). These measured absorption coefficients are shown in Figure 6-3. 83 Figure 6-3: Measured absorption coefficients –ln(I/Io) for the methylene blue in water solution (0.1 M). Error bars shown in light-gray. A potential of -1 V was applied to the working electrode (relative to the grounded carbon nanofoam electrode), and another spectrum was taken. For these spectra, light was measured for 0.2 s in order to measure during the period of time when the absorption was at its strongest, but before the applied potential was removed. These measurements had significantly more error, so these spectra were averaged for 26 data points (equivalent to a 10 nm span in wavelength) to increase the signal-to-noise ratio. The uncertainty in each of the resulting data points was estimated as the standard deviation of these 26 data points divided by the square root of 26, to estimate the standard deviation of the mean of these 26 points. The natural logarithm of the ratio of these spectra to the reference spectrum (when the cell was empty) were once again used to determine the absorption coefficients of the interface. The planar cell electrodes were then electrically connected for several minutes to allow the solution to return to its initial state. A 84 potential of -1.5 V was then applied, and another reflected spectrum was measured. The measured absorption coefficients for these applied potentials are shown in Figure 6-4. Figure 6-4: Measured absorption coefficients –ln(I/Io) for the methylene blue in water solution with different potentials applied to cell. Error bars shown in light-gray. A running average (over 10 nm) is depicted for data measured when -1 V and -1.5 V were applied. The measured absorption coefficients when -1 V and -1.5 V were applied to the working electrode were subtracted from the initial absorption coefficients to determine the change in the absorption coefficients of the interface when the potential was applied. These coefficients are shown in Figure 6-5. For these spectra, the error for each absorption coefficient was calculated in the same manner as before. For the data shown in Figure 6-5, the measured absorption coefficients when -1 V and -1.5 V potentials were applied were subtracted from the absorption coefficients when no potential was applied to determine the net change in the absorption coefficients. Hence, the errors in the net absorption coefficients were the square root of the sum of the squares of the 85 errors of the absorption coefficients when -1 V or -1.5 V were applied and when no potential was applied. Figure 6-5: Measured absorption coefficient when a potential was applied to the cell –ln(I/Io)V less the absorption coefficient when no potential was applied –ln(I/Io)o. Running averages of the measured data (over 10 nm) are depicted. Most absorption occurs between 575 nm – 775 nm, with a weak absorption peak around 780 nm also observed. 6.1.3 Analysis The absorption cross sections measured for these experiments were compared to known absorption cross sections of methylene blue monomer and dimer55. The absorption spectrum of trimer methylene blue was not available, but has been reported to peak at around 590 nm42. Data on higher methylene blue aggregates was not found in a literature review. Nevertheless, the absorption peaks of their spectra, theorized to occur at 550 nm or lower, did not appear to match the measured data. Leucomethylene blue was not included into these fits, as it does not 86 significantly absorb visible light. The previously reported absorption cross sections of the methylene blue monomer and dimer forms are shown in Figure 6-6. Figure 6-6: Absorption cross sections for monomer and dimer forms of methylene blue obtained from prior published work. A first attempt at modelling the initial absorption spectrum (shown in Figure 6-3) was done using a weighted sum of the methylene blue monomer and dimer absorption cross sections. Each of these absorption cross section spectra in Figure 6-6 was multiplied by a constant (representing the hypothesized concentration of the monomer or dimer multiplied by the path length of the light through the solution) that was varied; the resulting sum was then subtracted from the measured initial spectrum and the difference then squared. These values were then divided by the square of the experimental uncertainty and all these values were summed, which gave the chi-square statistic of the fit. The two constants used in this fit were varied in order to minimize this error metric. The resulting fit, as shown in Figure 6-7, is not as good as one might expect if only monomer and dimer were involved. 87 Figure 6-7: Initial absorption coefficients –ln(I/Io) fit as sum of methylene blue monomer and dimer absorption cross sections The trimer form of methylene blue has been previously reported to have a peak absorption wavelength of (590 +/- 10) nm, so this appeared to match the measured initial reflectance, although a quantitative fit was not possible since the absorption spectra of the trimer form of methylene blue was not available. At these concentrations, methylene blue has been observed to exist primarily in its trimer form42, so a component from trimer absorption would not be unexpected. Interestingly, the absorption spectra measured when potentials were applied, however, had a somewhat different shape. The absorption coefficients were again compared to the absorption spectra of methylene blue monomer and dimer to determine whether these forms of methylene blue could at least partially explain the shape. Once again, a fitting was done for these 88 absorption coefficients in a manner similar to that done for the initial spectrum. The resulting fits for the -1 V applied case, and the -1.5 V applied case, are shown in Figure 6-8. Figure 6-8: Measured absorption coefficients when a potential was applied to the –ln(I/Io)V less the absorption coefficients when a potential of 0 V was applied –ln(I/Io)o and a chi-square fit of this data using the absorption spectra of methylene blue monomer and dimer The resulting composition of methylene blue monomer and dimer for these fits is shown in Table 6-1. The uncertainty in the fitting parameters was found by varying the parameters until a range was found that increased the chi-square statistic by 2.3, which is the increase one would expect using two fitting parameters at the 68% confidence level56. The fits were not very good fits for the data, so the uncertainty in these fitting values simply gives the range of fitting values that minimized the chi-squared statistic with 68% confidence. Although the peak absorption wavelengths for the monomer and dimer approximately matched the measured data, the imperfect fit suggests that additional factors are involved. For example, if these particles were adsorbed onto the surface of the ITO, their absorption spectra 89 would likely be modified, and this could explain the altered absorption spectra. Unfortunately, absorption modification of this type has not been studied, and so no fitting was possible with the adsorbed spectra. One interesting aspect of these results is the apparent increase of methylene blue ions near the interface despite the applied potential being below the potential at which methylene blue ions reduce to leucomethylene blue (estimated to be -0.480 V in Chapter 4). Results such as these have been measured before in a system consisting of ITO submerged in a methylene blue solution57, although no explanation for the observation was given. One possible explanation for these results is that the absorption of light arises from adsorbed leucomethylene blue. Leucomethylene blue has been observed in other systems to acquire light-absorbing properties similar to methylene blue monomer and dimer when adsorbed58,59. The results and analysis performed here are far from conclusive, but they indicate this system presents an interesting opportunity for further research. Table 6-1: Composition of methylene blue monomer and dimer used for fitting Applied Potential Monomer (1020 m-2) Dimer (1020 m-2) Composition -1 V 0.108 +/- 0.001 0.082 +/- 0.001 56.9% Monomer (+/- 0.2%) 43.1% Dimer (+/- 0.2%) -1.5 V 0.160 +/- 0.001 0.122 +/- 0.001 56.8% Monomer (+/- 0.2%) 43.2% Dimer (+/- 0.2%) The results of this experiment suggest that the methylene blue dissolved in water initially exists as a mixture of monomer, dimer, and especially trimer, methylene blue. When a potential is applied to the solution, the ratios shift, and possibly surface effects modify the spectra somewhat. The key conclusion here is that the net-neutral system of species concentrated near to the ITO surface appeared to have absorption characteristics similar, although not exactly equal to, the methylene blue monomer and dimer ions. 6.2 Double Potential-Step Chronocoulometry As described in Section 3.2.3, double potential step chronocoulometry is a common technique used for analyzing electrochemical systems. This method involves applying a series of potentials to an electrochemical cell while measuring and recording the electrical currents 90 passing through the cell. The integral of these currents is used to determine the net charge through the cell over time. This type of experiment was performed with a planar cell and the net charges were analyzed at different applied potentials. 6.2.1 Experimental Design The planar cell used for this experiment was similar to that used for the experiments described in Chapter 4, with a working electrode that was 2 mm by 4 mm in size. The experimental setup used to apply potentials and measure the currents through the cell was also the same as that used for the planar cell. A 650 nm laser beam was focused and reflected from the working electrode interface with MB-H2O, and measured with the radiant flux measuring system described in Section 3.2.1. Preliminary experimentation was performed with a planar cell using different concentrations of methylene blue in water. Potentials were applied to these cells and the capacitances of the ITO/MB-H2O interface with these different concentrations were determined in the same manner as was done in Section 4.4. The capacitances of the electrode/solution interfaces appeared to be dependent on the concentration of dye in the cell. This suggested that the supercapacitance of the ITO/MB-H2O interface may be dependent on the concentration of methylene blue ions in solution. For this reason, the experiments described in this section were performed with four different solutions of varying MB concentrations. Unlike the preliminary experiments just described, these solutions had a fixed ionic concentration of 1.32 x 1026 ions/m3 (0.22 M), but with different electrolyte compositions in order to ensure that the electrolyte solution resistance was the same. This was done by mixing two solutions, one of 0.22 M MB in water and one of 0.22 M NaCl in water by volume. One of these solutions was composed of pure NaCl (0.22 M NaCl), one was composed of 1% MB and 99% NaCl (0.002 M MB and 0.218 M NaCl), one was 10% MB and 90% NaCl (0.02 M MB and 0.20 M NaCl), and the final solution was pure MB (0.22 M MB). The applied potential sequence to the planar cell was composed of electrical potential pulses of negative polarity that attracted methylene blue ions to the working electrode surface. The pulses were of four second duration, and the voltage of these pulses was incrementally varied from 0 V to -1 V over 2000 seconds. Over the following 2000 seconds, the voltage pulses 91 were incrementally returned from -1 V to 0 V. This applied potential sequence is shown in Figure 6-9. Figure 6-9: Potential sequence applied to the planar cell for double potential-step chronocoulometry. Potential pulses were applied for a period of four seconds. Scale of inset altered for visualization purposes. 6.2.2 Experimental Results The planar cell was first filled with the pure sodium chloride solution (0.22 M NaCl), and the sequence of potentials shown in Figure 6-9 was applied to the cell. The currents through a 900 Ω resistor in series with this cell were measured at a sampling rate of 350 Hz. The reflected flux fraction of the 650 nm laser beam incident at this interface was also recorded. Afterwards, the sodium chloride solution was removed with a syringe, and the 99% NaCl / 1% MB (0.218 M NaCl / 0.002 M MB) solution was injected into the cell. This process was repeated twice more to ensure the majority of the original NaCl solution had been removed. The potential sequence was then applied a second time, and the currents and flux fraction were measured and recorded. This process was then repeated for the 10% MB solution / 90% NaCl (0.02 M MB / 0.20 M NaCl) 92 solution, and finally for the pure methylene blue solution (0.22 M MB). The reflected flux fraction measured during these experiments is shown in Figure 6-10. Figure 6-10: Measured reflected flux fraction for four different MB/NaCl solutions. Measurements were taken with the same experimentally cell, performed sequentially in order of increasing MB concentration. This data suggests two important things. First, the 1% MB / 99% NaCl (0.218 M NaCl / 0.002 M MB) data showed the greatest permanent decrease in reflectance, equal to 22%, during the course of applied potentials. This was the first solution containing methylene blue dissolved in water that was tested in the experimental cell. The irreversible drop in reflectance measured during this experiment is consistent with a stable film of light-absorbing molecules adsorbing to the ITO surface. This adsorption appeared to be caused by the negative applied potential pulses, which attracted methylene blue ions to the surface. The amount of methylene blue ions, per area of electrode surface, required to absorb this much light is 1.19 x 1019 ions/m2. Assuming a 93 density equal to the density of solid methylene blue, this would be equivalent to an adsorbed layer at least 4.2 nm thick. The second important piece of information from this data is that the 10% MB / 90% NaCl (0.02 M MB / 0.20 M NaCl) solution exhibited the largest change in reflectance, and had the most reproducible and consistent reflectance changes. The 0.22 M methylene blue solution actually had reflectance changes that diminished at potentials near -1 V. The 0.02 M MB / 0.20 M NaCl solution was chosen to be studied when examining the charge flow through the cell because it exhibited the largest reproducible changes in reflectance. One peculiarity was noted when applied potentials to the cell were removed (the potential between working electrode and counter-electrode was returned to zero). When this was done, the reflectance of the interface increased back to near its original value as expected, but there was a very brief period where the reflectance dropped further (shown in Figure 6-11). Such a decrease in reflectance with the removal of the applied potential could be the result of leucomethylene blue oxidizing to methylene blue ions. However, the reverse process was not observed: when a potential was applied that reduces methylene blue to leucomethylene blue, a brief increase in reflectance was not observed. A definitive explanation for this phenomenon remains a possible opportunity for further research. The 10% MB / 90% NaCl solution exhibited the largest reversible changes in reflectance, although the measured flux fraction values took approximately 8 s to return to near their original value after the removal of the applied potential pulses, compared to approximately 2.5 s for the 100% MB solution. The measured flux fraction values from the planar cell described in Chapter 4 took approximately 1 s for the reflectance values to return to near their initial state after an applied potential pulse. The reason for the different lengths of time was unclear. 94 Figure 6-11: Measured flux fraction values dropped temporarily when applied potentials were removed. Dotted lines indicate the flux fraction values before the potential pulse was applied. Arrows indicate the relevant axes for each data set. 6.2.3 Analysis The currents through the planar cell were next analyzed to determine the nature of electrochemical phenomena occurring at the ITO/MB-H2O interface. This was done by integrating the measured currents as a function of time during the 4 s timeframe when potentials were applied to the cell. These integrations were done over different durations to determine the net charge that had passed through the cell during that period. 95 Figure 6-12: Accumulated charge through planar cell during chronocoulometry experiment Currents were integrated from the moment a given potential was applied to the cell to a time 0.1 s later to determine the net charge that had flowed through the cell during this 0.1 s period. This was done from 0 s up to 4 s, at which point the applied potential was removed. These net charges with respect to the square root of the integration times are shown in Figure 6-12 for the solution of 10% MB and 90% NaCl. As described in Section 3.2.3, when the charge accumulates in a manner proportional to the square root of the time from the application of a potential, this is an indication of a mass-transport limited reaction. If another type of reaction is also occurring, the extent of charge accumulation will be the sum of the charge accumulation from these two processes. The first portion of these curves did not show a linear trend, indicating that these currents were not limited by ions diffusing to the surface of ITO, but were limited by some other, unknown factor. On the other hand, when the applied potential to the cell was above 0.6 V, the charge accumulation showed a strong linear dependence toward the end of the applied potential 96 pulse. A few of these curves showed a clear change in the rate of charge accumulation, from a non-linear rate to a linear rate with respect to the square root of time (this occurs at a bit less than 1 s for the 0.70 V applied potential case). A linear dependence on charge accumulation with respect to the square root of time the potential has been applied indicates an electrochemical reaction limited by diffusion. A least-squares fit of the final second of these curves yielded the following linear fits: Table 6-2: Linear fit values for charge accumulation through cell vs. the square root of time Applied Potentials Slope (C/(m2∙√s) Intercept (C/m2) 1.00 6.210 +/- 0.002 2.530 +/- 0.003 0.95 6.086 +/- 0.003 2.612 +/- 0.005 0.90 5.917 +/- 0.002 2.539 +/- 0.004 0.85 5.766 +/- 0.002 2.704 +/- 0.004 0.80 5.646 +/- 0.002 2.592 +/- 0.003 0.75 5.588 +/- 0.001 2.610 +/- 0.003 0.70 5.629 +/- 0.001 2.281 +/- 0.003 Based on the Cottrell equation, equation (20) described in Section 3.2.3, the slopes of these fits would be expected to be largely independent of the applied potential, so the fairly consistent slopes are typical of diffusion-limited charge flow. The intercepts of these fits also appeared largely potential-independent, which would be consistent with an electrochemically active adsorbed layer on the ITO surface. The charge flow through an electrochemical cell with an electrochemically active adsorbed layer on the electrode and an electrochemically active solution species can be modelled with a modified Cottrell equation60: 𝑄(𝑡) = 2𝑛𝐴𝐶𝑞𝑒 √𝐷𝑜 𝑡 √𝜋 + 𝑛𝐴𝑞𝑒 Γ𝑜 + 𝑄𝑑𝑙 21 where n is the number of electrons involved in a reaction between the ion and electrode, A is the electrode area, C is the concentration of ions in the bulk solution, qe is the charge of an electron, Do is the diffusion constant of the ionic species, Γo is the number of ions adsorbed on the electrode surface, and Qdl is the charge through the cell due to the charging of the double-layer. Based on equation (21), one would expect the slopes of these curves to match, since the diffusion constants and ionic concentrations are the same from one applied potential to the next. 97 The slopes and intercepts of these fits, however, did vary in a statistically significant way with respect to each other, but this could be due to differences in the system from one applied potential to another. For example, the effective electrode area in contact with solution may vary slightly, or the local concentration of ions near the electrode surface may vary. Regardless, there were definite linear relationships, and fits of these linear portions had similar slopes and intercepts. The average slope for these fits was 5.8 +/- 0.2 C/(m2·√s). Using the Cottrell equation, and the concentration of methylene blue in the solution (1.2 x 1025 ions/m3 (0.20 M)), and assuming two electrons are involved in the electrochemical reaction (which is the number of electrons required to reduce a methylene blue ion to a leucomethylene blue), this slope corresponds to a diffusion constant of 1.79 +/- 0.06 x 10-12 m2/s. The diffusion constant for methylene blue ions in water is 7.8 x 10-10 m2/s. These differ by a factor of more than 400, indicating some mechanism was significantly inhibiting the diffusion to the surface. Such a process could be related to the adsorbed film on the ITO surface, which may inhibit electrontransfer from the electrode to the species in the electrolyte61. The intercepts for these fits represent charge that accumulated at the ITO surface that was limited by a process other than diffusion, which would be the sum of the charge flow due to the reduction of the adsorbed species on the ITO surface and the charge flow from the double-layer capacitance. The intercept of these fits was approximately constant for different applied potentials, equal to 2.6 +/- 0.2 C/m2. The charge through the cell due to the charging of the electric double-layer did not seem to represent a significant portion of this charge, as these intercepts were largely potential-independent at potentials above ~0.7 V. Assuming the adsorbed species are methylene blue ions, and these ions reduce to leucomethylene blue, then the intercepts of these fits represent the reduction of 8.1 x 1018 ions/m2. The estimated amount of ions adsorbed to the ITO surface, based on the irreversible reflectance drops previously mentioned (show in Figure 6-10), was 1.2 x 1019 ions/m2. Both the consistent intercepts for these fits, and the irreversible reflectance changes observed when negative potentials were applied to the working electrode, are evidence of a strongly absorbed layer of methylene blue ions on the ITO surface that undergoes reduction at applied potentials below -0.7 V. The minimum number of ions needed to explain the measured reversible reflectance changes for the 0.02 M MB solution was 3.18 x 1019 ions/m2 (calculated in Section 4.5), which is four times larger than the number of ions in the adsorbed film. This indicates the reduction of the 98 adsorbed layer does not represent enough charge to account solely for the effective capacitance, or for the observed reflectance changes, indicating the diffusion-limited charge flow is at least partially responsible for these effects. 6.3 Summary of the Phenomenon Based on the spectroscopy measurements and chronocoulometry analysis, the following can be concluded: The initial absorption spectrum of the solution indicates the presence of the trimer form of methylene blue. The absorption spectrum of the ions stored on the electrode/electrolyte solution interface when potentials were applied to the cell was not consistent with trimer ions. They also were not consistent with any combination of free methylene blue monomers or dimers, although the absorption characteristics were similar. Negative applied potential treatments created an irreversible drop in the reflectance of the interface, indicating the formation of an adsorbed layer of light-absorbing molecules onto the ITO surface. Charge flow through the cell was primarily governed by two processes: one limited by diffusion and another due to the reversible reduction of adsorbed ions on the ITO surface. The results from the work in this chapter provide a brief overview of the complex electrochemical phenomena occurring at the ITO/MB-H2O interface. Thorough electrochemical analysis of this interface was not the goal of this project; the experiments and results described here were meant to give a preliminary look into the possible mechanisms occurring at this interface that will help guide further research. 99 Chapter 7: Electro-Optic Large-Angle Diffraction For the final experiment of this thesis, the size-scale of the interdigitated electrodes in a diffraction grating cell were reduced in order to create a reversible electro-optic diffraction grating that was capable of diffracting light to an angle of 33°. The diffraction efficiency measured for the diffraction grating cells from Chapter 5 (hereafter referred to as 10 µm pitch diffraction grating cells) was 0.7% of the incident laser flux, and since the results of these experiments indicated the dye was pulled to within less than 100 nm of the ITO surface, it was hypothesized that the size-scale of the electrodes could be reduced substantially without a significant loss of diffraction efficiency. To test this hypothesis, a cell containing interdigitated electrodes separated by 800 nm (i.e., having a diffraction grating with a pitch of 800 nm) was built and tested. 7.1 Design Requirements The experimental cell consisted of two ITO films on glass plates, with the ITO film on one plate patterned with a design consisting of two interdigitated electrodes. Two of the design requirements of the diffraction grating cell were equivalent to those of the diffraction grating cell described in Chapter 5: the relative area of the grounded ITO electrode needed to be many times larger than the area of the interdigitated electrodes, and there needed to be sufficient solution so that the bulk concentration of methylene blue ions in water did not change significantly when a portion of the ions were pulled to the electrodes. A diagram of the experimental cell is shown in Figure 7-1. A photograph of one of the experimental cells is shown in Figure 7-2. There were only two design constraints that differed from the 10 µm pitch diffraction grating cell, the diffraction grating spatial frequency and the interdigitated pattern of the electrodes. These were subtly altered in a way that helped the alignment of the diffraction grating during measurements. The pitch of the interdigitated electrodes was made small enough that there was no initial diffraction pattern associated with the electrode spacing. In other words, the angle of the first order diffraction peak, found using equations (8), (9), and (10), had a z-component that was less than zero, which was not possible in this system. For incident light normal to a diffraction grating, this state of no diffraction occurs when the diffraction grating pitch is reduced to less than the wavelength of light. However, at greater incident angles, such as those used for the 100 present experiments, the smallest diffraction grating pitch at which light diffracts into a 1st order beam is greater than the wavelength of light. Figure 7-1: Electro-optic diffraction grating cell for large-angle diffraction. The ITO film on the top substrate has been patterned into two electrically isolated electrodes in an interdigitated design. Electrical contact was made with these electrodes using silver epoxy (not shown). The diffraction grating pitch was also designed so that when it was doubled, a new diffraction peak (referred to as the interstitial order diffraction peak to be consistent with the terminology used in Chapter 5) was created. The diffraction grating pitch was doubled in the same manner in which it was for the experiments described in Chapter 5; a potential was applied between the electrodes to pull dye ions to one of the two conductors, and hence every second electrode. The pitch was then returned to its original value by removing the applied potential and allowing the dye ions to return to the bulk solution. In this way, the cell could reversibly switch between a state where reflected light diffracted, and a state where the reflected light did not diffract. 101 Figure 7-2: Photograph of diffraction grating cell filled with methylene blue in water solution. The top substrate consists of an ITO film patterned into an interdigitated design. Electrical contact is made with these electrodes using silver epoxy, and the red and yellow wires shown above. The bottom electrode is maintained at ground, and connected to via silver epoxy and the black wires shown above. The optimal dimensions of the electrodes were determined by simulating the diffraction grating in GSolver (the diffraction grating solver program described in more detail in Section 3.4.2). The parameters of the grating that were used to model the grating in GSolver, such as the ITO thickness, the index of refraction of the materials, and the thickness and index of refraction of the increased concentration of dye ions near one of the interdigitated electrodes, were those determined for the 10 µm pitch diffraction grating, as described in Chapter 5. The expected flux fraction of the 0th order, 1st order (when present), and the interstitial order that would be created if the pitch were doubled, were then found using GSolver for different diffraction grating pitches (shown in Figure 7-3). 102 Figure 7-3: Grating pitch dimensions and estimated flux fraction of 1 st order and interstitial order diffraction peaks when potentials of -1 V are applied to interdigitated electrodes. These results indicated that a diffraction grating pitch of greater than 480 nm was necessary for diffraction to occur when a potential was applied to the electrodes, and a pitch of less than about 950 nm was needed to prevent diffraction from occurring when no potential was applied. Further, it indicated that a larger diffraction grating pitch generally resulted in more light diffracted with an applied potential. For these reasons, a diffraction grating pitch of 800 nm was selected. The interdigitated pattern of this diffraction grating required a modification of previous patterns. In the earlier work described in Section 5.2, the procedure used to align a laser beam onto the diffraction grating area relied on the initial diffraction pattern from the grating. However, the grating pitch for this cell was designed to have no initial diffraction pattern. A method for achieving alignment of this grating could have been developed to overcome this 103 limitation, but a very convenient and effective way of alignment was to make a slight modification to the diffraction grating pattern itself. The pattern of this diffraction grating was designed to have two different diffraction grating spatial frequency components. The first was the already-planned 800 nm pitch for the interdigitated electrodes. The second was achieved by making every 9th electrode three times the normal electrode width. This resulted in a faint initial diffraction pattern for use in alignment of the laser beam on the grating. This unique pattern incorporated a second spatial frequency into a diffraction grating without disrupting the underlying spatial frequency. A schematic of this new multi-pitch diffraction grating is shown in Figure 7-4. 8 µm 800 nm 1.2 µm Figure 7-4: Interdigitated diffraction grating designed with a primary spatial frequency (800 nm pitch) and an additional secondary spatial frequency (effective pitch of 8 µm) component to aid the alignment process Simulations in GSolver with this new diffraction grating pattern indicated this would reduce the flux fraction of the newly created diffraction peak by approximately one third, but this known reduction was accounted for when analyzing experimental measurements and it was a worthwhile compromise to make it practical to align the laser with the grating. 104 7.2 Experimental Set-Up The experimental set-up consisted of an optical arrangement and a measurement system similar to that described in Chapter 5. The differences with this experimental set-up were the optical arrangement, which was designed to focus a laser beam onto the much smaller diffraction grating area, and the system used to hold the experimental cells, which was designed so that the cell location and orientation could be precisely controlled to align the incident laser beam on the diffraction grating area. Due to the size-scale of the interdigitated electrodes, photolithography was not appropriate for fabricating the diffraction grating, so focused ion beam milling was used. The final grating area milled by the ion beam machine was 100 µm by 100 µm in area. It was desirable to have all the incident laser flux strike this area. If only half the energy of the laser beam were striking the diffraction grating area, for instance, then the measured diffraction peak flux fractions would only be half as large. Furthermore, determining the amount of energy incident on the grating would complicate the measurement of flux fraction values. This problem was avoided by ensuring the laser beam was entirely focused onto the diffraction grating area. The laser beam needed to be focused to a much smaller area for these gratings than for the 10 µm pitch diffraction grating cells. Due to the oblique angle of the incoming laser, the laser needed to be focused to an area of less than 50 µm by 50 µm. This was achieved using two lenses and two apertures. A 2 mm diameter aperture was placed in front of the laser diode to limit the size of the beam and remove light that was outside the desired collimated beam. A 4 cm focal length lens was then used to focus the beam, and a second 2 mm diameter aperture was used again to remove unwanted stray light. A second lens of focal length 20 cm was placed 40 cm in front of the focus of this beam to refocus the beam onto the diffraction grating area. These two lenses were used instead of a single lens in order to focus the beam over a longer distance, in order to provide ample room for the experimental platform. The optical arrangement is shown in Figure 7-5. In order to ensure that the laser was focused to an area of less than 50 µm by 50 µm, the minimum beam width of the laser was measured. This was done by directing the laser beam into the entrance of the integrating sphere with the photodiode described in Section 3.2.1. A straight edge was then incrementally raised into the beam to block a portion of the beam. The sharp edge 105 of a razor blade was used as the straight edge. The measured flux fraction from the photodetector was recorded at different heights of the razor blade to determine the amount of light being blocked by the razor blade edge as a function of the height of the edge. The minimum beam width of the laser was measured to have an approximately Gaussian profile, with a standard deviation of 10 µm. A laser beam of width 40 µm (a width which includes approximately 95% of the laser energy) will diffract due to circular diffraction at a 1st order angle of 1.1°. Therefore, the diffraction-limited angular beam spread of the laser was estimated to be +/- 1.1°. Figure 7-5: Optical arrangement for 800 nm pitch diffraction grating measurements. Alignment of this highly focused laser beam onto a diffraction grating area of only 100 µm by 100 µm required more precision in the location and orientation of the experimental cells as compared to the 10 µm pitch diffraction grating cells. Accordingly, the apparatus holding these experimental cells was designed to allow more precise placement and orientation of the cells. The cells were placed on a sample holder whose angle could be adjusted in small increments, which will be referred to simply as an angular platform. This angular platform was mounted on a platform that could be incrementally moved in three directions, which will be referred to as an xyz platform. The angular platform was set such that the incident beam struck the grating at an angle of 71.5°, 10° above the critical angle of 61.5°. The angular spread of the incident beam was 1.1°, so 71.5° was chosen as the incident angle to ensure no light was striking 106 the grating at less than the critical angle. The xyz platform was adjusted until the diffraction pattern associated with the secondary spatial frequency of the diffraction grating (with an effective pitch of 8 µm) was at its maximum intensity. Alignment of the laser beam onto the diffraction grating area proved to be difficult. Precise alignment (adjustments on the order of 10s of micrometers) of the beam could be done by measuring the diffraction pattern with an integrating sphere and photodiode, but initial coarse alignment (adjustments on the order of millimeters) proved to be difficult due to the very faint initial diffraction pattern from the 650 nm laser beam. A 405 nm laser diode was added to the optical arrangement to aid in alignment. This beam was directed so that it reflected from two mirrors, whose orientations could be precisely adjusted. The two beams were then oriented approximately orthogonal to one another, and a beam splitter was placed at the location where the beam intersected. The orientations of the mirrors were then adjusted until the 405 nm laser beam was aligned parallel to the 650 nm laser beam. Finally, a 4 cm focal length lens was used to diverge the 405 nm laser beam so that when both beam struck a 40 nm focal length lens, the two beams would be focused to within a few microns of each other. The smaller wavelength of the 405 nm laser meant that the reflected light from this beam had an initial diffraction pattern associated with the 800 nm electrode spacing. The human eye is not very sensitive to this wavelength, so a fluorescent paint coated screen was placed behind the cell during alignment to view the diffraction pattern associated with this laser, in order to convert the light pattern to a more readily visible wavelength. In this way, the diffraction pattern of the 405 nm laser beam could be used to guide the placement of the beams onto the diffraction grating area. In practice, the dispersion in the prism glass caused the two laser beams to focus to points separated by approximately 200 µm, but since this was a known offset it was not problematic. The 405 nm beam was very useful for getting the laser beam to within 200 µm of the grating area. Once that was done, the 405 nm laser was turned off, and the 650 nm laser beam was guided by the previously mentioned diffraction from the low frequency spatial component. These additional details of the experimental setup used for optical measurements are also shown in Figure 7-5. The diffraction pattern from the 405 nm laser was also useful for placing the entrance to the integrating sphere in the proper location to measure the newly created diffraction peak. This 107 was possible because the 405 nm laser diode had an 8th order diffraction peak associated with the secondary spatial frequency of the grating (effective pitch of 8 µm) that nearly coincided with the location of the newly created diffraction peak. The angle, in glass, of the 8th order peak for the 405 nm laser, was, using equation (7): sin−1 8 · 405 𝑛𝑚 = 15.53° 1.513 · 8,000 𝑛𝑚 The angle, in the glass, of the newly created diffraction peak (the m = ½ order for the 800 nm pitch grating or, equivalently, the 1st order for the 1600 nm pitch grating) was sin−1 0.5 · 650 𝑛𝑚 = 15.58° 1.513 · 800 𝑛𝑚 The integrating sphere was then placed such that the 8th order peak from the 405 nm laser beam was directed into the entrance port of the sphere. The 405 nm laser beam was used for this purpose because its 8th order peak was significantly more intense than the 650 nm laser peak. The angle, in air, when accounting for refraction from the prism, was 33° with respect to the 0 th order beam. Finally, after completing the alignment process, the 405 nm laser was turned off, and the integrating sphere location was adjusted, if necessary, until the 5th order diffraction peak from the diffraction pattern arising from the secondary spatial frequency of the diffraction grating was directed into the entrance port. This was the location where the newly created diffraction peak would be created, because the 5th order peak of an 8 µm pitch diffraction grating will diffract light to the same angle as the 1st order peak of a 1.6 µm diffraction grating (the primary spatial frequency of the grating is 800 nm, but when a potential is applied the spatial frequency will decrease by a factor of two, hence it will have a pitch of 1.6 µm). 7.3 Sample Fabrication The creation of the interdigitated grating required prepping the electrode, and milling the interdigitated pattern using a focused ion beam machine. 7.3.1 Electrode Preparation The ITO coated glass electrodes were prepared for ion beam milling in several steps: ablation of a portion of the ITO using an industrial laser-cutter, ultrasonic cleaning of the ITO surface, and insulating the area of the ITO surface that would not be milled. 108 The ITO coated glass electrode containing the diffraction grating needed to be milled into two electrically-isolated electrodes. This required ITO film to be removed along the entire electrode, a length of 2.5 cm, with no defects electrically connecting the two electrodes. The focused ion beam milling machine was not capable of milling lengths of more than a few hundred microns without repositioning the beam. For these reasons it was impractical for an ion beam milling machine to successfully mill over the lengths necessary to achieve full electrical isolation, so a portion of the ITO was ablated from the glass using an industrial laser cutter before milling, leaving only a small portion of ITO film electrically connecting the two sides of ITO film, hereafter referred to as the ITO bridge. This way, the focused ion beam only needed to mill a small portion of ITO to complete electrical isolation. A Universal Laser Systems VLS 4.60 commercial CO2 laser cutter62 was used to ablate the ITO film from the glass plate. This laser cutter had a precision of about 100 µm, and slight changes in the height of this layer also changed the beam size, so the actual width of the bridge was chosen to be 300 µm in order to ensure that the resulting width would be at least 100 µm. The resulting width of the bridge from this ablation process ranged from 100 µm, to as much as 500 µm. The length of the ITO film bridging portion was 1 mm. This length was chosen to be sufficiently large so that either side of the ITO coated glass electrode could be covered with an insulating layer by hand, without unintentionally covering the bridging portion as well. The area ablated by the industrial laser is shown in Figure 7-6(a). One problem with this process was that the ablation was found to generate small molten silica particles that deposited on and became irreversibly bonded to the ITO film. These particles blocked the ion beam during the milling process and prevented the ITO film underneath from being milled, creating problematic electrical shorts in the diffracting grating pattern. Several different methods were attempted to overcome this problem, but only one method proved successful. Using this method, a thin layer of oil was coated onto the ITO using a spin-coater before laser cutting to protect the ITO from adherence of the silica particles (shown in Figure 7-7(a)). The oil used was Cargille Type B non-drying immersion oil, typically used in microscopy47. This oil was chosen because of its high viscosity, purity, and because it dissolved in Toluene, which made it easily removable afterwards. The oil was spin-coated onto the ITO coated glass electrode using the Chemat Technology Spin-Coater KW-4A63. The spinning was done for 15 seconds at 1,750 RPM, and then 60 seconds at 4,750 RPM. While the oil was spin109 coated in a uniform layer, it eventually began to congeal. The congealing process took approximately one hour before the oil thickness became non-uniform, so the laser ablation process was done immediately after spin-coating to minimize this problem. After the spincoating process, the industrial laser was used to ablate the oil and the ITO film underneath. The oil film coating on the ITO bridge remained during this process, and any silica particles located there were removed when the protective oil layer was later removed. No silica particles were found to be bonded to the ITO film when this oil layer method was used to protect it. After ablation with the laser, the ITO films on the glass plates were then immersed in various solvents and treated ultrasonically in a Branson 200 ultrasonic cleaner. First, the ITO/glass electrodes were immersed in a solution of Toluene to remove the oil and were treated ultrasonically for five minutes. These electrodes were then placed in a second solution of Toluene, to remove any residual oil, and treated for another five minutes. Afterwards, the electrodes were placed in a solution of ethanol, and finally distilled water, then again treated in the ultrasonic cleaner for five minutes. Next, the portions of ITO coated glass that would not be a part of the diffraction grating were covered in an insulating layer. The insulating layer was comprised of RTV silicone sealant, which was the same material used for the 10 µm pitch diffraction grating. The silicone was applied by hand with a cotton swab, with the aid of a stereo microscope, to the entire ITO film except for the ITO bridge. 110 4 cm ITO Bridge (a) ITO Coated Glass 2.5 cm 200 µm Glass A A 1 mm ITO Film ITO Film Removed via Laser Cutter (b) Glass Plate Section “A-A” Exposed ITO Film— See Figure 7.6 (c) Silicone on ITO Coated Glass Glass 200 µm 2.5 cm Figure 7-6: ITO coated glass electrode preparation. In (a), ITO film has been removed via laser cutter to leave a 200 µm thick ITO film bridge electrically connecting the film. In (b), a cross section of this electrode is depicted with exaggerated ITO film thickness for illustrative purposes. In (c), silicone has been applied to the electrode leaving only a small portion of the ITO bridge exposed. 111 Just as with the 10 µm pitch diffraction grating, a permanent interstitial diffraction order was prevented by applying the same potentials across the ITO/MB-H2O interfaces. This required not only that equivalent patterns of applied potential to the electrodes vs. time be the same, but also required that the two electrode areas in contact with the methylene blue in water solution be equal. The precise alignment capabilities of the joint scanning electron microscope and focused ion beam milling machine were used to ensure the interdigitated pattern was milled on the ITO film at a point where the two electrode areas were equivalent. This meant that the exposed area on the ITO film need not be centered exactly on the ITO bridge, which greatly simplified the preparation of the ITO coated glass electrode. The area of the ITO film covered in silicone is shown in Figure 7-6(c). After the silicone was applied, it was left to cure overnight. The electrode was then cleaned using distilled water in an ultrasonic cleaner for five minutes, and left in a clean hood until the interdigitated electrode pattern was milled onto the exposed ITO film at the Centre for High-Throughput Phenogenomics at the University of British Columbia. A scanning electron microscope (SEM) image of the ITO film just after ion beam milling, taken using the Helios NanoLab 650 is shown in Figure 7-7(b). This picture is an SEM image of approximately the same area on the ITO glass electrode that was shown in the magnified portion of Figure 7-6(c). 112 Figure 7-7: SEM image of ITO coated glass electrode before milling. In (a), silica particles are bonded to the ITO film. In (b), the ITO surface is clean and ready for ion beam milling. In Figure 7-7(a), an ITO coated plate of glass is imaged using the SEM capability of the ion beam machine. On the ITO film are silica particles that have strongly adhered to the glass. In Figure 7-7(b), also imaged using the SEM, oil was used to protect the ITO film in the manner already described, and so no silica particles appeared on the ITO film. Figure 7-7(b) also shows 113 the ITO bridge, which in this figure is the light rectangular area centered in the image, of approximately 600 µm length and 200 µm width. An interdigitated pattern was later milled in this area. Above and below the bridging portion are areas where the ITO film was ablated using the commercial laser-cutter. These regions above and below the ITO film consist of glass, and have fractured as a result of the industrial laser ablation process. Some silicone is visible on the far left-hand portion of the image. 7.3.2 Focused Ion-Beam Milling The focused ion-beam milling process was done in three steps, which will be described in detail in this section. First, the interdigitated pattern was milled into the ITO film. Second, four lines were milled from the diffraction grating area to completely electrically isolate the two electrodes. Finally, the ITO films were treated to oxygen plasma to remove contaminants from the surface of the ITO film. The prepared electrodes were milled using the Helios NanoLab 650 located at the Centre for High-Throughput Phenogenomics at UBC. This type of milling machine is used to mill into materials and then image them with the scanning electron microscope. It is not typically used for the patterning of films, especially for the relatively large area needed to be milled for these gratings. The problems that were overcome, and the final milling process used to mill the electrodes, are discussed in Appendix A. Only the results of the milling process will be discussed in this section. SEM images of the milled pattern are shown in Figure 7-8(a) and (b). In this SEM image, the dark portions show areas where the conductive ITO film has been removed with the ion beam milling process to reveal the glass material underneath. The light portions indicate the non-milled areas, where the ITO film is still present. Next, electrical isolation of the ITO into two electrically-separated electrodes was completed by milling a portion of ITO along a line, from the interdigitated pattern to the areas ablated by the laser. This pattern is shown in Figure 7-9. 114 Figure 7-8: SEM images of milled interdigitated design in ITO coated glass electrode. Light regions are ITO film, while dark regions indicate locations where the focused ion beam removed ITO film, exposing glass. 115 In Figure 7-9, the interdigitated pattern is observed slightly above center on the ITO bridge. Two dark rectangles can be seen above and below this interdigitated pattern. These rectangles are dark as a result of four lines milled into the ITO film extending from the four corners of the interdigitated pattern across the ITO film to the regions where the ITO film was ablated via the laser-cutter. These four milled lines complete electrical isolation of the two sides of ITO film. Two lines would have been sufficient for this purpose, but four lines were used so that the ITO area between these lines could be checked for conductivity. If one of the lines had not completely milled through the ITO film the area between these lines would appear light due to the material still having an electrical path to ground. With no defects, these areas were electrically isolated from ground and consequently accumulated charge during the imaging process, resulting in the regions that appear darker than the neighboring ITO film. In Figure 7-9, the regions between these lines appear dark-gray. The very dark area at the top of the image in Figure 7-9 is non-conductive glass. Finally, the ITO coated glass was treated using oxygen plasma. This was done because an unknown material, believed to be carbon from an imperfect vacuum in the machine, was found to be deposited on the ITO film when it was imaged with the SEM. An SEM image of an ITO film surface previously subjected to SEM imaging is shown in Figure 7-10. In this image, a rectangular area previously imaged via SEM imaging appears slightly darker than surrounding ITO film. This area is shown contained within the dotted rectangle in the image. 116 Glass Interdigitated pattern One of four milled lines extending from grating to glass (highlighted in red) ITO film electrically isolated from the substrate ITO film on glass Figure 7-9: SEM image of milled interdigitated design, which separates the ITO film into two isolated electrodes. Diffraction grating cells fabricated for this project not treated with oxygen plasma were found to have considerably lower capacitance than was observed with other cells, so it appeared that a chemically pure ITO film was necessary to achieve supercapacitance. To remove unwanted surface impurities, oxygen plasma was injected into the milling chamber immediately after the milling process. The electrode was then immersed with the oxygen plasma for 60 seconds. Further SEM imaging indicated that the oxygen plasma successfully removed the unwanted surface layer. Finally, the electrode was removed from the ion beam milling chamber, and a diffraction grating cell was constructed and used for experimental measurements. 117 Unknown film deposited on ITO surface Figure 7-10: Unknown film deposited on ITO after SEM imaging 7.4 Experimental Results Several diffraction gratings were constructed using the methods outlined in the previous section. The first of these diffraction grating cells were tested by applying the same sequence of applied potentials used for the 10 µm pitch diffraction grating cell (shown in Figure 5-7), but the cell did not have the expected capacitance, and appeared to have a larger leakage current. These results will be discussed later in this section, but first one result from these initial tests is worth noting. 118 Figure 7-11: Potential sequence applied to diffraction grating (a), and the measured flux fraction of the interstitial order peak (b). The angle of this diffraction peak with respect to the 0th order beam was 33°. One diffraction grating was tested with a slightly different sequence of applied potentials, shown in Figure 7-11(a). These potentials consisted of potential pulses that decreased in magnitude from 0 V down to -2 V in 160 mV increments, and then back to 0 V in 160 mV increments. The positive potentials applied to the working electrode were, for this potential sequence, reduced in magnitude to prevent unwanted electrochemical degradation due to chemical reactions between chlorine ions and the ITO electrode. The flux fraction values of the interstitial order diffraction peak that were measured while this potential sequence was applied are shown in Figure 7-11(b). Almost no change in the interstitial order was observed until applied potentials of approximately -1.6 V were applied. At these potentials, the flux fraction of 119 this order varied significantly, reaching a maximum fraction equal to nearly 0.9% of the incident laser light, a fraction actually greater than the measured flux fraction from the 10 µm pitch diffraction grating described in Chapter 5. The dynamic response of the grating from these measurements is also worth noting. One of the peaks is shown in Figure 7-12. For this diffraction peak, the removal of the interstitial order diffraction peak happened over a duration of less than 50 ms (the sampling frequency for this experimental run was only 20 Hz, so further resolution of this change was not determined). These results, while interesting and representing an opportunity for further research, were difficult to reproduce. Thus, it was decided to better understand why these devices were responding differently, both electrically and optically, than previous diffraction grating cells to the same applied potential sequence, and then to determine a way to achieve reversible diffraction at a lower applied potential. Figure 7-12: Flux fraction of interstitial order exhibiting a short dynamic response (< 50 ms). Applied potential to one interdigitated electrode was -1.75 V (depicted here as a positive potential for ease of viewing), while the applied potential to the second interdigitated electrode was 0.44 V. 120 To further understand the different performance of these cells, a planar cell with a planar electrode area equal to the area of a diffraction grating cell with interdigitated electrodes separated by 800 nm (hereafter referred to as an 800 nm pitch diffraction grating cell) was constructed. The currents through this planar cell were measured and recorded while a potential of -1 V was applied to the working electrode for three seconds. After three seconds, the applied potential was set to zero and the currents from the cell were once again measured and recorded. For comparison, the currents through an 800 nm pitch diffraction grating cell were measured and recorded while a potential of -1 V was applied to one of the interdigitated electrodes, and a potential of 0 V was applied to the second. These potentials were applied for three seconds while the currents through the cell were measured and recorded. The potential to both interdigitated electrodes were then set to zero, and the currents were once again measured and recorded. The net charges through both of these cells were then compared during periods of applied potentials and periods of applied potentials of 0 V. These charges are shown in Table 7-1. Table 7-1: Net charge area density through a planar and diffraction grating cell Planar Cell Charge area density (C/m2) 800 nm Pitch Diffraction Grating Cell Charge area density (C/m2) -1 V Applied Potential 41.1 C/m2 55.6 C/m2 Applied Potential Removed -15.0 C/m2 -3.0 C/m2 The amount of charge through both cells during periods of applied potentials differed by about 35%, but the differences in the amount of charge through the cells during periods of no applied potentials differed by a factor of 5. These differences were consistent with the 800 nm pitch diffraction grating cell having a smaller leakage resistance across the ITO/MB-H2O interface. A small leakage resistance would allow more current to flow from the electrode to the electrolyte solution, increasing the net charge through the cell during periods of applied potentials, and it would also prevent the capacitor from fully charging, which would explain the much smaller amount of charge from the cell during periods of no applied potential. It was hypothesized that the differences in leakage resistances could be due to the extremely small distance between electrodes of the 800 nm pitch diffraction grating cell. A new sequence of applied potentials was then designed, one that would ensure the interfaces of the interdigitated ITO and methylene blue in water would fully charge. This was done by applying 121 the same potential to both interdigitated electrodes for a period of time so that there was no potential difference across the leakage resistance between these electrodes. The potential to these electrodes was applied until both ITO/MB-H2O interfaces were fully charged, and then the potential to one of the electrodes was switched to one that repels methylene blue ions (or equivalently, attracts chlorine ions). This ensured that the interfaces would fully charge, although it was unclear whether this charge storage would be stable. The applied potential sequence designed to do this was composed of 3 s long pulses of applied potentials, and 77 s periods of no applied potentials, similar to that used for the 10 µm pitch diffraction grating cell. The major difference with this sequence of applied potentials from the one applied to the 10 µm pith diffraction grating cells was that one of the electrodes had methylene blue ions drawn to it for two seconds, and then the voltage polarity was switched to repel methylene blue ions (and attract chlorine ions). A new circuit was designed to apply these sequences of applied potentials to the experimental cell, depicted in Figure 7-13. A LabVIEW program operating on a computer was used to apply two different potential sequences to two inverting operational amplifiers. Two 220 kΩ resistors were placed in series with the experimental cell, and the voltage across these resistors was measured and recorded. The applied potential sequence to the two electrodes is shown in Figure 7-14. Figure 7-13: Circuit diagram used to apply potentials to diffraction grating cell. The large-area counter electrode was always grounded, while two different potential sequences were applied to the interdigitated electrodes. 122 Each of the applied potential pulses shown in Figure 7-14 had a 2 s duration during which both electrodes were given the same applied potential, and one second where one of the electrodes was switched to a potential of opposite polarity, and equal to 1/4th the absolute magnitude. The potential applied to one of these electrodes is shown with a solid black line, while the potential to the other electrode is shown by a dotted blue line. Figure 7-14: Applied potentials sequence to the 800 nm pitch diffraction grating. Inset not to scale. Using the experimental setup described, and applying the sequence of potentials to the 800 nm pitch diffraction grating cell shown in Figure 7-14, the newly created diffraction peak flux fraction was observed, measured, and recorded. These measured flux fractions are shown in Figure 7-15. The envelope of the applied potential sequence (shown to be positive for visualization purposes) is shown by the dotted line. The reflectance of laser light from the cell before any potential differences were applied was measured to be 86% of the incident laser light. 123 Figure 7-15: Measured diffraction peak flux fraction for 800 nm pitch diffraction grating. Arrows indicate the relevant axes for each data set The initial measured diffraction peak flux fractions were not zero. This is because, as already mentioned, the interdigitated electrode design was modified slightly to add a secondary spatial frequency to the grating to aid in alignment. The 5th order diffraction peak from this secondary spatial frequency was located at the same angle as the newly created diffraction peak. This was useful for accurately placing the integrating sphere and photodiode for measurement, and is at least partly the reason the initial measured radiant flux fraction is not zero in Figure 7-15. The graph in Figure 7-16 was expanded along the time axis to better show the optical response at an applied potential of -0.8 V. Initially, since the potentials applied to both electrodes were equivalent, there was no increase in the flux fraction of the diffraction peak. When the polarity of the voltage applied to one of the electrodes switches, however, the diffraction peak 124 flux fraction rapidly increased, and then began to decrease, possibly due to the leakage resistance across the capacitors. Figure 7-16: Measured diffraction peak flux fraction for 800 nm pitch diffraction grating. Arrows indicate relevant axes for each data set. 7.5 Discussion Each successive diffraction peak shown in Figure 7-15 was created by creating a layer of increased methylene blue ions next to alternating interdigitated electrodes. In other words, potentials were applied in such a way as to attract ions to one of the two sets of interdigitated electrodes to create one diffraction peak, and for the subsequent diffraction peaks the potentials were applied in such a way as to attract the ions to the second of the two interdigitated electrodes. The fact that successive peaks exhibit approximately the same intensity encouragingly shows that the interfaces next to both interdigitated electrodes were reacting to the applied potentials in a similar manner. 125 The maximum measured diffraction order was not observed at applied potentials of -1 V, but actually occurred at an applied potential of around -0.8 V. Further, the measured diffraction order flux fractions were not as great when the potential sequence envelope was decreasing as when increasing. The reason for this is unknown, but could possibly be due to the formation of an electrically passive layer of adsorbed particles to the ITO film, rendering successively larger portions of ITO film unable to contribute to the electrolytic capacitance. The maximum observed diffracted flux fraction was equal to 0.31% of the incident laser light. As previously mentioned, the addition of the 8 µm diffraction grating pitch necessary for alignment caused a reduction in the expected observed flux fraction by one third. Had the 8 µm pitch not been present, presumably the flux fraction would be 0.45%. The maximum flux fraction measured for the 10 µm pitch diffraction grating cell was equal to just over 0.7% of the incident laser light. Given the difficulty of creating and measuring the smaller-scale diffraction grating, the slightly smaller measured flux fraction seems quite reasonable. The change in the sequence of applied potentials to the cell could also account for the difference, although the exact effect of this applied potential sequence is unknown, and beyond the scope of this work. Overall, the sub-micron grating performed as hoped. The time-scale at which optical changes occurred was also shorter than for the planar cell or the 10 µm diffraction pitch grating cells. In the latter cases, optical changes occurred over the course of seconds, while in the former case the responses were on the order of the hundredths of seconds. The time-scale for these changes is quite important in some applications of beam steering, so reducing the time it takes to diffract light can have important implications for its application in industry. The different time-scales for optical switching were likely due to the different sequence of applied potentials used for the cells in this chapter. For the 800 nm pitch diffraction grating cell, the potential sequence was designed to accumulate charge at both electrodes at once, and then to remove the potential and repel these charges away from the electrode surface. A possible explanation for the time-scales at which the interstitial order was formed was because the repelling process is a faster response than the attracting process. This is consistent with what was observed for the 10 µm diffraction grating, in that the creation of the interstitial order required seconds to be created, but only hundredths of seconds to be removed. 126 Finally, the large degree of reversible diffraction shown in Figure 7-12, as well as the short time response of this peak, while difficult to reproduce, are indicative of possibilities for potential improvements to the efficiency and response time for this method of electro-optic diffraction. 7.6 Summary In summary, the system of ITO electrodes submerged in methylene blue dye ions in water was shown to produce reversible, electro-optic diffraction with a newly created diffraction peak at an angle of 33° with respect to the 0th order beam. This new diffraction peak was measured to have similar diffraction efficiency to that of a system at much larger size-scales. The diffraction efficiency measured, when the effect of the two-pitch design is accounted for, was 0.45%. This compared favorably to the much larger-scale grating which had an efficiency of 0.7%. Fabrication of the gratings gave more insight into the mechanism for supercapacitance and the control of the grating showed a size-scale dependent nature to these types of gratings. The required electrical control of the 800 nm pitch grating was significantly different than for the 10 µm pitch grating. The 800 nm pitch grating required a new sequence of applied potentials in order to create the diffraction peaks. This suggests that the distance between electrodes has an impact on the electrical control of the diffraction grating. Work remains to be done to further understand and improve this method for electrically-controlled diffraction, but the results from this work show that this method has promising future applications. 127 Chapter 8: Conclusion The work in this thesis provided an unusual opportunity to bridge several different fields of experimental research, including optics, electrochemistry, and materials science. While the goal of this thesis was to develop and understand the physics of an electro-optic diffraction grating, much was learned relevant to these other fields as well. Specifically, the reflectance of the interface of a transparent conductive material, ITO, and an electrolyte solution with light absorbing particles, methylene blue dye ions dissolved in water, was shown to be reversibly altered by as much as 50%. These changes in reflectance are made possible by the supercapacitance of this interface, which was measured to be more than 40 F/m2. This is the first electrolytic supercapacitor that makes use of transparent materials and an electrolyte solution with light-absorbing particles. An electrolytic cell using these materials was made by patterning an ITO film on a glass plate into two interdigitated electrodes. This cell was experimentally shown to achieve reversible electro-optic diffraction, with a newly created diffraction peak that was measured to reversibly reach 0.7% of the incident laser flux. Modelling of this system indicated that interdigitated electrodes could be scaled down to sub-micron size-scales. The ITO/MB-H2O interface was measured using two electrochemical methods: spectroelectrochemistry and double potential-step chronocoulometry. The results of these experiments suggested that the mechanism for supercapacitance was due to the reversible deposition of a net-neutrally-charged concentration of particles near the ITO surface with lightabsorption characteristics similar to methylene blue monomer and dimer ions. Evidence was also found that indicated the existence of an electrically active adsorbed layer of ions on the ITO film, which underwent reversible reduction when potentials were applied between electrodes. An electrolytic cell with 800 nm pitch interdigitated electrodes was fabricated through the use of a focused ion beam machine. This cell was shown to achieve electro-optic diffraction that reversibly diffracted light to an angle of 33°, and could achieve a reversible flux fraction of 0.45% of the incident light at these angles. This work also provided the opportunity to integrate measurement and fabrication techniques that are not often used in other fields. Specifically, the use of a transparent conductor in an electrolytic cell allowed the opportunity for performing electrochemical methods in atypical ways. In situ spectroelectrochemistry was possible due to the transparency of the ITO 128 electrode. The spectrum of light that reflected by means of total internal reflection from the ITO/MB-H2O interface depended solely on the absorption properties of the electrolyte solution within only a few hundred nanometers of the ITO surface. This allowed for the direct measurement of ions directly surrounding the electrode. Further, by knowing the absorption spectra of different ions in the electrolyte solution, it allowed inference of the ionic composition. This technique was not only possible when the electrode was submerged in the electrolyte solution, but was also used to gather direct evidence for the ionic species drawn to the ITO under an applied electric field, something rarely possible in other systems. Chronocoulometric techniques were also performed using this unique system. The flux of a laser beam reflecting from the ITO/MB-H2O interface was measured along with current through the electrolytic cell, and the accumulated charge through the cell was correlated with the reflectance of the interface. The results of these correlations were useful in determining the type of electrochemical phenomena that gave rise to optical changes in the system. Much work was also done on sub-micron scale lithography. Focused-ion beam milling is a relatively new field, and one in which large-scale patterning is rather rare. A unique way to perform lithography over large distances, with high precision, was outlined in Appendix A. This work may be useful in other situations that require the fabrication of nanoscale electrodes. The experiments on diffraction grating cells described in this thesis were meant only to determine whether the supercapacitance of an electrolytic capacitor with transparent electrodes could achieve electro-optic diffraction at large diffraction angles. The purpose was not to propose device designs, or to optimize the diffraction efficiency, speed of response, or maximize the lifetime of these gratings (which were sometimes only useful for one applied potential sequence). Nevertheless, an alteration to the grating that could be useful for a device, as well as modifications to the grating that could be done to improve various aspects of the grating will be briefly mentioned here. The diffraction gratings described in this thesis were capable of only two spatial frequencies, and hence could only reversibly deflect light to one fixed angle. In principle, however, if each electrode was controlled independently, then the number of spatial frequencies that could be achieved would be equal to the number of electrodes, ranging from the distance between electrodes to the width of the diffraction grating. A device operating in this manner 129 could achieve large angle light-beam steering with a nearly continuous control of deflection angle. One immediate alteration to the diffraction grating that could improve the diffraction efficiency would be to incorporate blazing into the electrodes. Blazing is a common technique in diffraction gratings designed to increase the diffraction efficiency of a specific diffraction peak order64. Accordingly, producing electrodes with angled faces, rather than flat faces, the diffraction efficiency could be greatly increased. Another way to improve the performance of the diffraction grating cells would be to increase the speed at which the diffraction orders are created and removed. Some applications of beam steering, such as wavelength division multiplexing devices, require a response time less than 10 ms,2 so a reduction of the dynamic response of the device is necessary for it to be useful in such applications. Evidence that the speed of response of the grating could be greatly increased was found and described in Chapter 7, when a potential of -1.6 V was applied to a diffraction grating cell and the timeframe for the removal of a diffraction peak was less than 50 ms. The rate at which the diffraction peaks were created, however, was shown to be primarily limited by diffusion. Despite this limitation there remain possibilities for improving the dynamic response of the grating. One possibility would be to use a supersaturated solution. This could be achieved by using a very thin cell in which most of the ions would always be attracted to the active electrodes, but in which the pattern of their absorption would shift to cause the desired diffraction change. Loading the methylene blue ions into the cell would require several fluid exchanges, because the effective concentration per unit volume would exceed the saturation limit, but this should not be too difficult. A system working in this manner could effectively reduce the diffusion distance to the working electrode from tens of µm to as small as the evanescent penetration depth (of order hundreds of nanometers). There are several other factors that could also be improved substantially. One possibility is the composition of the electrolyte solution. As shown in Section 6.2, the electrolyte composition had a significant effect on the performance and lifetime of the electrolytic cell. A lower concentration of methylene blue in an equivalent ionic concentration was shown to have a larger optical response and appeared to have a longer lifetime as well. Different compositions of electrolytes, and different concentrations of methylene blue, are other factors that could be experimented with to further improve the performance of the device. 130 Another aspect that warrants further research is the design of the applied potential sequence. Initial tests indicated the lifetime of the cell to be greatly reduced at potentials below -1 V, although different electrolyte concentrations appeared to mitigate this. The magnitude of potentials applied could be altered to increase the diffraction efficiency or improve the lifetime. The optimal shape of the potential sequence pulses also warrants further research. In conclusion, a method for switchable electro-optic diffraction at an angle of 33° without the need for nanoporous films was experimentally verified. There remains much work to be done to improve the diffraction efficiency, time-scale of optical changes, and lifetime of the cell. Nevertheless, this method shows promise for use in applications where electrically controlled diffraction is needed at large angles, such as in telecommunications or data storage systems. 131 References 1. Whitehead L, Huizinga J, inventors; 3M Innovative Properties Company and The University of British Columbia, assignees. Electrostatically-controlled diffraction gratings using ionic electrophoresis. patent US7576905 B2. Aug 18, 2009. 2. Ahderom S, Raisi M, Lo K, Alameh KE, Mavaddat R. Applications of liquid crystal spatial light modulators in optical communications. High Speed Networks and Multimedia Communications. 2002:239-242. 3. Scibor-Rylski M. Total-internal-reflection electro-optic diffraction deflector/modulator. Electron Lett. 1973;9(14):309-310. 4. Schmid K, Waters K, Dingerson L, et al. Lidar 101: An introduction to lidar technology, data, and applications. National Oceanic and Atmospheric Administration (NOAA) Coastal Services Center. 2008. 5. Chao T, Hanan JC, Reyes GF, Zhou H, inventors; California Institute of Technology, assignee. Holographic memory using beam steering. patent US7251066 B2. July 31, 2007. 6. Srinivasan R, Vijayaraj A. Mobile communication implementation techniques to improve last mile high speed FSO communication. In: Trends in network and communications. Springer; 2011:55-63. 7. Henniger H, Wilfert O. An introduction to free-space optical communications. Radioengineering. 2010;19(2):203-212. 132 8. Comstock JM, Ackerman TP, Mace GG. Ground‐based lidar and radar remote sensing of tropical cirrus clouds at nauru island: Cloud statistics and radiative impacts. Journal of Geophysical Research: Atmospheres (1984–2012). 2002;107(D23):AAC 16-1-AAC 16-14. 9. Younse JM. Mirrors on a chip. Spectrum, IEEE. 1993;30(11):27-31. 10. Duncan BD, Bos PJ, Sergan V. Wide-angle achromatic prism beam steering for infrared countermeasure applications. Optical Engineering. 2003;42(4):1038-1047. 11. Mach P, Wiltzius P, Megens M, et al. Electro-optic response and switchable bragg diffraction for liquid crystals in colloid-templated materials. Physical Review E. 2002;65(3):031720. 12. Ngoi B, Venkatakrishnan K, Lim L, Tan B. Angular dispersion compensation for acousto-optic devices used for ultrashort-pulsed laser micromachining. Optics Express. 2001;9(4):200-206. 13. Kuriyama K, Nishikawa Y, Shioyama T, Uesugi Y, inventors; Matsushita Electric Industrial Co., Ltd., assignee. Laser cutting method and apparatus for effecting said method. patent US5138131 A. 1992. 14. Dudley D, Duncan WM, Slaughter J. Emerging digital micromirror device (DMD) applications. Proc SPIE. 2003;4985:14-25. 15. Younse JM. Projection display systems based on the digital micromirror device (DMD). Proc SPIE. 1995;2641:64-75. 133 16. Stanimirović I, Stanimirović Z. Optical MEMS for telecommunications: Some reliability issues. Advances in Micro/Nano Electromechanical Systems and Fabrication Technologies, Assistant Professor Kenichi Takahata (Ed.), ISBN. 2013:978-953. 17. Hecht E. The kerr and pockels effects. In: Optics. Fourth ed. Addison-Wesley, Massachusetts; 1998:368-370. 18. Sun L, Kim J, Jang C, et al. Polymeric waveguide prism-based electro-optic beam deflector. Optical Engineering. 2001;40:1217-1222. 19. Davis SR, Farca G, Rommel SD, Martin AW, Anderson MH. Analog, nonmechanical beam-steerer with 80 degree field of regard. Proc SPIE. 2008;6971:69710G69710G-11. 20. Apter B, Efron U, Bahat-Treidel E. On the fringing-field effect in liquid-crystal beam-steering devices. Appl Opt. 2004;43(1):11-19. 21. Mossman MA. Spectral control of total internal reflection for novel information displays. [Ph.D]. University of British Columbia; 2002. 22. Rakic AD, Djurišic AB, Elazar JM, Majewski ML. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl Opt. 1998;37(22):5271-5283. 23. Hrudey P, Martinuk M, Mossman M, et al. Application of transparent nanostructured electrodes for modulation of total internal reflection. Proc SPIE. 2007;6647:66470A-66470A-12. 134 24. Hrudey P, Martinuk M, Mossman M, et al. Variable diffraction gratings using nanoporous electrodes and electrophoresis of dye ions. Proc SPIE. 2007;6645:66450K-66450K12. 25. Windbacher T. Debye huckel model. http://www.iue.tuwien.ac.at/phd/windbacher/node62.html. Accessed February 2, 2015. 26. Bard A, Faulkner L. Models for double-layer structure. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:544-545. 27. Bard A, Faulkner L. The gouy-chapman theory. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:546-551. 28. Bard A, Faulkner L. Stern's modification. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:551-554. 29. Hecht E. Optics 4th edition. Optics, 4th Edition, Addison Wesley Longman Inc, 1998. 1998;1:3. 30. Fluckiger D. GSolver version 5.2 user's guide. http://www.gsolver.com/UserManual.pdf. Updated 2012. Accessed February 3, 2015. 31. Bass A, Paur R. The ultraviolet cross-sections of ozone: I. the measurements. In: Atmospheric ozone. Springer; 1985:606-610. 135 32. Fowles G. Amplitudes of reflected and refracted waves. In: Introduction to modern optics. Second ed. Dover Publications, Inc.; 1989:43-44. 33. Fowles G. The evanescent wave in total internal reflection. In: Introduction to modern optics. Second ed. Dover Publications, Inc.; 1989:48-49. 34. Bard A, Faulkner L. Capacitance and charge of an electrode. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:12. 35. Victoria blue B. http://www.sigmaaldrich.com/catalog/product/sigma/94890?lang=en®ion=CA. Accessed January 28, 2015. 36. Farjami E, Clima L, Gothelf KV, Ferapontova EE. DNA interactions with a methylene blue redox indicator depend on the DNA length and are sequence specific. Analyst. 2010;135(6):1443-1448. 37. Więckowski A. Spectroelectrochemistry of methylene blue. In: Interfacial electrochemistry: Theory, experiment, and applications. Marcel Dekker; 1999:519. 38. Sagara T, Niki K. Surface processes and adsorption states of methylene blue at graphite electrode surfaces in an acidic medium: An electroreflectance study. Langmuir. 1993;9(3):831-838. 136 39. Impert O, Katafias A, Kita P, Mills A, Pietkiewicz-Graczyk A, Wrzeszcz G. Kinetics and mechanism of a fast leuco-methylene blue oxidation by copper (II)–halide species in acidic aqueous media. Dalton Transactions. 2003(3):348-353. 40. Lee S, Mills A. Novel photochemistry of leuco-methylene blue. Chem.Commun. 2003(18):2366-2367. 41. Spencer W, Sutter JR. Kinetic study of the monomer-dimer equilibrium of methylene blue in aqueous solution. J Phys Chem. 1979;83(12):1573-1576. 42. Braswell E. Evidence for trimerization in aqueous solutions of methylene blue. J Phys Chem. 1968;72(7):2477-2483. 43. Papeschi G, Costa M, Bordi S. Electrochemical behavior of methylene blue and its leucoform at the mercury electrode. J Electrochem Soc. 1981;128(7):1518-1521. 44. USB 2000+ (custom). http://oceanoptics.com/product/usb2000-custom/. Updated 2015. Accessed February 3, 2015. 45. Bard A, Faulkner L. Potential step under diffusion control. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:162-163. 46. Giannuzzi L, Stevie F. A review of focused ion beam milling techniques for TEM specimen preparation. Micron. 1999;30(3):197-204. 137 47. Cargille microscope immersion oils. http://www.cargille.com/immeroil.shtml. Updated 2014. Accessed January 16, 2015. 48. MXT angle platform. http://www.siskiyou.com/tilt-bases_mxt.shtml. Accessed January 26, 2015. 49. LabView system design software. http://www.ni.com/labview/. Updated 2014. Accessed January 26, 2015. 50. Prabhakar A, Mukherji S. Microfabricated polymer chip with integrated U-bend waveguides for evanescent field absorption based detection. Lab on a Chip. 2010;10(6):748-754. 51. Papeschi G, Costa M, Bordi S. Electrochemical behavior of methylene blue and its leucoform at the mercury electrode. J Electrochem Soc. 1981;128(7):1518-1521. 52. MARKETECH international inc. carbon nanofoam. http://mkt- intl.com/materials/aerogel/carbon-nanofoam/. Updated 2015. Accessed January 23, 2015. 53. NovaFlex fiber optic illuminator - 115v. http://www.wpiinc.cn/en/Products/BrowseBy-Category-en/Microscopyen/Light-Sources-en/NOVAFLEX-Fiber-Optic-Illuminator115v.html. Updated 2008. Accessed January 23, 2015. 54. Ocean optics SpectraSuite(r) spectrometer operating software. http://oceanoptics.com/wp-content/uploads/SpectraSuite.pdf. Accessed January 23, 2015. 55. Jockusch S, Turro NJ, Tomalia DA. Aggregation of methylene blue adsorbed on starburst dendrimers. Macromolecules. 1995;28(22):7416-7418. 138 56. Avni Y. Energy spectra of X-ray clusters of galaxies. Astrophys J. 1976;210:642-646. 57. Matsuda N, Santos JH, Takatsu A, Kato K. In situ observation of absorption spectra and adsorbed species of methylene blue on indium-tin-oxide electrode by slab optical waveguide spectroscopy. Thin Solid Films. 2003;445(2):313-316. 58. Sagara T, Niki K. Surface processes and adsorption states of methylene blue at graphite electrode surfaces in an acidic medium: An electroreflectance study. Langmuir. 1993;9(3):831-838. 59. Sagara T, Iizuka J, Niki K. Electroreflectance study of the redox reaction of methylene blue adsorbed on a pyrolytic graphite electrode. Langmuir. 1992;8(3):1018-1025. 60. Bard A, Faulkner L. Chronocoulometry. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods - fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:603-605. 61. Bard A, Faulkner L. Dynamical elements, characteristic currents, and limiting behavior. In: Harris D, Swain E, Robey C, Aiello E, eds. Electrochemical methods fundamentals and applications. Second Edition ed. John Wiley and Sons, Inc.; 2001:610-616. 62. Universal laser systems VLS 4.60. http://www.ulsinc.ca/products/vls460/. Updated 2015. Accessed January 16, 2015. 63. KW-4A spin coater for R&D thin films & coatings. http://www.chemat.com/chematscientific/KW-4A.aspx. Accessed January 19, 2015. 139 64. Hessel A, Schmoys J, Tseng D. Bragg-angle blazing of diffraction gratings. JOSA. 1975;65(4):380-384. 140 Appendices Appendix A: Ion Beam Milling Techniques Microfabrication is the process of creating structures of micrometer size-scale. This process is often used to create integrated circuits with wiring of order micrometers. Microfabrication of these circuits is typically done using photolithography. In this thesis, photolithography was used to fabricate interdigitated ITO films on glass plates, with the width of the interdigitated digits equal to 6.5 µm. Photolithography, however, are incapable or unreliable at creating structures when the feature sizes are less than approximately 1 µm. An alternative to photolithography is focused ion-beam milling, which can be used to create patterns when the structure sizes are as small as a few nanometers. However, using these techniques for milling large areas (>10-10 m2, or roughly 10 µm by 10 µm), or where the milling time is long (more than about 5 minutes) causes problems due to beam misalignment and beam drifting. This appendix will outline a process for milling such patterns where these problems can be mitigated or avoided altogether. The procedures described in this appendix were performed using the FEI Helios NanoLab DualBeam. The machine is a combined focused ion-beam (FIB) and scanning electron microscope (SEM) located at the University of British Columbia, in Vancouver, Canada. 1. The procedure described here can be summarized in the following steps. 2. Determine ion beam milling current 3. Determine ion beam milling time 4. Import or construct the desired pattern 5. Set the number of passes of the ion beam Determining the Milling Current The first step in preparing to ion beam mill is to determine the ion beam current. The ion beam flux from the source is constant. The size of the beam is controlled using variable aperture. The size of the opening in this aperture determines the size of the beam. The current that strikes the material is based only on the diameter of the beam. In most cases one chooses the diameter to be as high as possible given the desired feature sizes. Using larger current results in a larger beam diameter, and hence less resolution. The beam current can range 141 from approx. 1 pA to 100 nA. The beam size can be directly estimated from the beam current using the following formula: 𝐷 = 𝑎 · √I A1 where D is the diameter of the ion beam, a is a value that was fit experimentally to relate the beam current to the beam diameter (for the Helios NanoLab DualBeam this value was estimated to be 2.64 x 10-3 m·√s/√C), and I is the beam current (C/s). Determining the Milling time Next, it is best to estimate the length of time the milling process will take. This can be estimated using the following formula: 𝑉 𝑇 = 𝐼 ·𝑉 𝐷 A2 where T is the total milling time, V is the total volume of material that needs to be removed, I is the ion beam current, and VD is the volume of material removed per dose of charge. The value of VD depends on the material that is being ablated, but these values typically range from 0.15 x 10-9 m3/C to 1.0 x 10-9 m3/C. Creating the Bitmap Once the total mill time is determined, the FIB machine needs to be given a pattern to be milled. For simple structures, this can often be done by building a pattern on the user-interface by inserting a sequence of lines, circles, polygons, etc. For more complex patterns, or for large patterns, a 24-bit bitmap can be used to control the machine. In the simplest case, a black-andwhite bitmap can be created, where white pixels will indicate locations where the ion beam will mill, and black pixels indicate places where the beam will be blocked. The Helios NanoLab DualBeam allows the user to import a bitmap as large as 24 MB. Since the image format is 24bit (3 bytes per pixel), this equates to a total of over 8 million pixels, or an image a bit larger than 2,800 by 2,800 pixels. 142 Figure A-1: Example of a 4 x 4 bitmap The size-scale of each pixel depends on the area that is milled. For instance, if one wanted to mill the simple square pattern depicted in Figure A-1 into a material, and one wanted the size of the milled area to be 1 µm, each pixel would represent an area of 250 nm by 250 nm. The beam current would then need to be set to about 9 pA to obtain a beam size of about 250 nm in diameter. Setting the Number of Passes Finally, the user typically enters the total depth they want the ion beam to mill. When milling begins, the ion beam mills in a raster pattern, milling successively deeper into the material on each pass of the ion beam until the user-defined depth is reached. The total number of passes of the beam can often be of order thousands or more. For small size-scales, this milling process works well, however this process does not work well for larger size-scales. An SEM image of a pattern milled in this fashion is shown in Figure A-2. 143 Figure A-2: FIB milling of a 15 nm thick ITO film on glass. The desired pattern was an interdigitated pattern. The milled pattern in Figure A-2 appears blurred, and the final pattern appears almost tilted from the original pattern. This is a common problem when milling large patterns over long periods of time. The problem shown in Figure A-2 arose primarily from the drift of the ion beam over time. As the ion beam finished each pass, and attempted to move back to the origin of the pattern, the drift of the ion beam caused each successive milled pattern to be slightly offset from the previous pass of the beam. This is exacerbated by the large distance the ion beam must move from the end of the pattern to the beginning. The result is a finished pattern that appears blurred from the desired pattern. These problems can be prohibitive when milling large areas or when milling over large time-scales. An alternative way to mill, however, that avoids these problems is to set the ion beam to mill the pattern in a single pass. One can set the number of passes in the software to be equal to one, or for more complicated patterns with differing milling depths, one can use the 144 following formula (which follows directly from equations (A1) and (A2)) to estimate the necessary dwell time at each point: 𝑉 𝑡 = 𝐼·𝑉 = 𝐷 𝐷2 𝑧 4 𝐷2 ·𝑉𝐷 𝑎2 = 𝑧·𝑎2 4𝑉𝐷 A3 where z is the desired depth into the material one wants the ion beam to mill at the desired location. Figure A-3: FIB milling of 15 nm ITO printed on glass using only one pass of the beam. Light areas indicate unaltered ITO, while dark areas in the image indicate areas where the ITO has been removed with the ion beam, revealing the glass underneath. The images in Figure A-3 show what the ion beam milling machine is capable of, when constrained to a single pass. Note that a large area was milled, with fine resolution, in over 8 minutes of milling time. Summary A technique was designed to minimize problems associated with the drift of a focused ion beam while performed lithography of nanometer size-scales. This technique was used to pattern a 100 µm by 100 µm area of an ITO film on a glass plate into an interdigitated design. Milling was done over several minutes, but there were no noticeable problems with the drift of the ions beam. This technique may be useful for operating a focused ion beam in similar applications. 145 Appendix B: Huygens-Fresnel Based Calculations Huygens-Fresnel Principle The Huygens-Fresnel principle states that every point on a wavefront serves as a source of spherical secondary point sources, known as wavelets. The complex field value at some other point in space is the superposition of all these wavelets, considering their amplitudes and phases, summed over the surface of a sphere centered at that point. The Fresnel reflections and optical thicknesses of the interfaces and materials in the diffraction grating are used to determine the amplitude and phase of the wavelets lying on the diffraction grating plane. The radiant intensity of each diffraction peak is calculated using the superposition of these wavelets in the far-field limit. Using this principle, the field value at some point P can be found by determining the superposition of a series of wavelets at a fixed distance from this point. Each one of these wavelets emits a spherical wave described in terms of its complex amplitude, U(r). The amplitude of the wave from this point source at a distance r from the source and with wave vector k can be written as: 𝑈(𝑟) = 𝑈𝑜 𝑒 𝑖𝑘𝑟 𝑟 The complex field value at some point P is found by summing up all the wavelets on the surface of a sphere of radius r from the point. For one point source the irradiance, I(r) [w/m2], can be found by taking the absolute square of this complex amplitude. 2 𝐼(𝑟) = |𝑈(𝑟)|2 = |𝑈𝑜 𝑒 𝑖𝑘𝑟 | 𝑟 Every wavelet on the surface of a sphere of radius r centered at the point P must be summed to determine the field value. This is often impossible to solve analytically, although a few assumptions were made to simplify the problem. First, for distances much larger than the dimensions of the diffraction grating, the plane of the diffraction grating was assumed to lie on the surface of a sphere. The wavelets everywhere else on the surface of this sphere were zero, as no wavefront ever passed through these points. Second, quantities were calculated in terms of the radiant intensity (w/Sr), which removed the 1/r dependence in the calculations. Experimental measurements were done using an integrating sphere and photodiode, which measured the radiant flux entering the integrating 146 sphere port. The radiant flux was determined from the radiant intensity by integrating this intensity over the appropriate angles measured by the integrating sphere. The radiant intensity was found by multiplying the irradiance by the surface element dSr (the area in a differential solid angle at a distance r from the origin). In the case of a single point source, this can be written in terms of the differential solid angle dΩ. 2 𝐼𝑆𝑟 (𝑟, 𝜃, 𝜑) = |𝑈(𝑟)|2 𝑑𝑆𝑟 = |𝑈𝑜 𝑒 𝑖𝑘𝑟 | 𝑟 2 sin 𝜃𝑑𝜃𝑑𝜑 = |𝑈𝑜 |2 𝑑Ω 𝑟 The radiant flux that would be measured by the photodiode was found from the radiant intensity by integrating over the appropriate angles. The coordinate system was defined such that the z-axis ran through the center of the integrating sphere port (wherever it was placed). The angular radial size of the integrating sphere port was defined to be θ’, and so the integral was: 𝜋+𝜃 ′ 𝜋 𝑅(𝑟) = 2 ∫ ∫ 0 𝜋 𝐼𝑆𝑟 (𝑟, 𝜃, 𝜑) sin 𝜃𝑑𝜃𝑑𝜑 Next, the light-emitting surface (or in the case of the diffraction gratings modeled in this thesis, the surface that is reflecting light) was approximated as a series of wavelets. For this approximation, the amplitude of the waves from each source depended on how many wavelets were used. The complex phase of each of these sources depended on the angle from the line perpendicular to the diffraction grating plane. For two wavelets (depicted in Figure B-1), the radiant intensity at a distance r and angle α is: 𝐼𝑆𝑟 (𝑟, 𝛼) = | 2 𝑈𝑜 1 1 ( + 𝑒 𝑖𝑘𝑥 sin 𝛼 )| 𝑟 2 𝑑Ω 2 𝑟 𝑟 + 𝑥 sin 𝛼 In the far-field, r is much greater than x · sin(α), and so the equation can be simplified to remove the 1/r dependence. 𝐼𝑆𝑟 (𝑟, 𝛼) = | 2 𝑈𝑜 (1 + 𝑒 𝑖𝑘𝑥 sin 𝛼 )| 𝑑Ω 2 147 α α v v x Figure B-1: Two Huygens-Fresnel wavelets separated by a distance x If more wavelets are used for the approximation, the field at a point P is calculated as the superposition of all the wavelets. If the diffraction grating area has area A, and it is approximated using N equally-spaced wavelets, then each wavelet is approximating the radiation from an area dA, where dA = A/N. The radiant intensity at a point P is then: 𝐴/𝑑𝐴 2 𝑑𝐴 𝑖𝑘𝑥 sin 𝛼 𝐼𝑆𝑟 (𝑟, 𝛼) = |𝑈𝑜 ∑ 𝑒 𝑚 | 𝑑Ω 𝐴 𝑚=1 For a square light-emitting area, with sides of length L, this can be written as: 𝐿2 /𝑑𝐴 2 𝑈𝑜 𝐼𝑆𝑟 (𝑟, 𝛼) = | 2 ∑ 𝑑𝐴 · 𝑒 𝑖𝑘𝑥𝑚 sin 𝛼 | 𝑑Ω 𝐿 𝑚=1 As dA → 0, the number of wavelets becomes infinite, and the equation becomes an integral: 2 𝑈𝑜 𝐿 𝐿 𝐼𝑆𝑟 (𝑟, 𝛼) = | 2 ∫ ∫ 𝑒 𝑖(𝑘𝑥 sin 𝛼) 𝑑𝑥 𝑑𝑦 | 𝑑Ω 𝐿 0 0 If the grating is uniform along the y-direction (as is essentially the case for the diffraction gratings created in this thesis), then the integral simplifies to only an integral in the x-direction: 148 2 𝑈𝑜 𝐿 𝐼𝑆𝑟 (𝑟, 𝛼) = | ∫ 𝑒 𝑖(𝑘𝑥 sin 𝛼) 𝑑𝑥 | 𝑑Ω 𝐿 0 For general cases, where L >> 𝜆, the integral will be zero and hence the only resulting wave from the wavelets will be the plane wave normal to the plane of point sources (depicted in Figure B-2). Wavefront v v v v v v dx Figure B-2: Multiple Huygens-Fresnel wavelets constructively interfering to create a wavefront However, this integral is not generally zero if the amplitude or phase of the point sources varies periodically. A periodic change results in diffraction. v 0 v d/2 v d v 3d/2 v 2d 5d/2 Figure B-3: Two groups of wavelets with a phase varying periodically over a distance d In Figure B-3, the phase of the point sources varies periodically over a distance d for a total length L. One group of point sources oscillates with complex amplitude U1, and the other 149 group oscillates with amplitude U2, and out of phase with the first group by γ radians. The resulting radiant intensity at an angle α in this case would be written in the following way. 𝑑 3𝑑 2𝑈1 2 2 𝐼𝑆𝑟 (𝑟, 𝛼) = | (∫ 𝑒 𝑖𝑘𝑥 sin 𝛼 𝑑𝑥 + ∫ 𝑒 𝑖𝑘𝑥 sin 𝛼 𝑑𝑥 + ⋯ ) 𝐿 0 𝑑 2 𝑑 2𝑑 2𝑈2 𝑖𝛾 + 𝑒 (∫ 𝑒 𝑖𝑘𝑥 sin 𝛼 𝑑𝑥 + ∫ 𝑒 𝑖𝑘𝑥 sin 𝛼 𝑑𝑥 + ⋯ )| 𝑑Ω 𝑑 3𝑑 𝐿 2 2 If L is assumed to be very large (relative to the wavelength), then all these terms will sum to be zero, except at angles when the terms constructively interfere. The angles at which this occurs are governed by the standard diffraction grating formula: 𝑚 · 𝜆 = 𝑑 · sin 𝛼𝑚 If L is large, then the radiant intensity will have some value at the angles determined by the diffraction grating equation, but will quickly fall to zero at any other angle. As the length of L approaches infinity, the radiant intensity can be written in the following way, where δ is used to signify the Dirac delta function: 2 𝑑 𝑑 2𝜋𝑚𝑥 2𝜋𝑚𝑥 1 2 𝐼𝑆𝑟 (𝛼) = 𝛿(𝛼𝑚 − 𝛼) | (𝑈1 ′ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑈2 ′𝑒 𝑖𝛾 ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 )| 𝑑Ω 𝑑 𝑑 0 2 Next, the expected measured quantity at the photodiode can be found by integrating over the angles allowed into the integrating sphere port. As long as the integrating sphere allows all the light in at a given angle αm, and does not allow light from other diffraction peak angles, then the measured radiant flux of each diffraction peak, R(m), simplifies in the following way: 2 𝑑 𝑑 2𝜋𝑚𝑥 2𝜋𝑚𝑥 1 2 𝑅(𝑚) = ∫ 𝐼𝑆𝑟 (𝛼) 𝑑Ω = | (𝑈1 ′ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑈2 ′𝑒 𝑖𝛾 ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 )| 𝑑 𝑑 0 2 The integrals in the above term can also now be evaluated quite easily, even for an arbitrary width, w, of the first group of point sources. 2 𝑤 𝑑 2𝜋𝑚𝑥 2𝜋𝑚𝑥 1 𝑅𝑚 = | (𝑈1 ′ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑈2 ′𝑒 𝑖𝛾 ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 )| 𝑑 0 𝑤 𝑅𝑚 = | 2 2𝜋𝑚𝑤 1 (𝑒 𝑖( 𝑑 ) − 1) (𝑈1 ′ − 𝑈2 ′𝑒 𝑖𝛾 )| (𝑚 ≠ 0) 2𝜋𝑚𝑖 For an angle of 0° (the 0th order peak), the resulting radiant flux is: 𝑅0𝑡ℎ = |𝑈1 ′ 𝑤 𝑑−𝑤 2 + 𝑈2 ′𝑒 𝑖𝛾 | 𝑑 𝑑 150 By setting w to be equal to 0 or d, the normalization constants can be determined. The amplitude and phase of these constants is just the incident electric field amplitude multiplied by the electric field amplitude reflectance, R*, or transmission, T* (depending on the application). Note R* and T* are generally complex numbers. For the case of a surface reflecting incident light, the resulting electric field amplitude is: 𝐸 = 𝐸𝑜 𝑅1∗ 𝑤 𝑑−𝑤 + 𝐸𝑜 𝑅2∗ 𝑑 𝑑 The mth order diffraction peak (m≠0) radiant flux is then: 𝑅𝑚 = | 2 2𝜋𝑚𝑤 1 (𝑒 𝑖( 𝑑 ) − 1) (𝐸𝑜 𝑅1∗ − 𝐸𝑜 𝑅2∗ )| 2𝜋𝑚𝑖 The radiant flux of the diffraction peaks are then given by the following equations: 𝑅0𝑡ℎ = |𝐸𝑜 |2 |𝑅1∗ 𝑅𝑚 = 𝑤 𝑑−𝑤 2 + 𝑅2∗ | 𝑑 𝑑 |𝐸𝑜 |2 𝜋𝑚𝑤 sin2 ( ) |𝑅1∗ − 𝑅2∗ |2 (𝜋𝑚)2 𝑑 For two different groups of wavelets, this will give the measured radiant flux values. To model the newly created diffraction peak radiant flux values created for the work in this thesis, requires accounting for four wavelet groups described in the next section. Modelling New Diffraction Peaks Using the Huygens-Fresnel Principle Modelling of the diffraction peaks in this thesis was done by summing up the wavelets from the surface of the diffraction gratings, where the glass met the ITO or electrolyte solution. The amplitude and phase of these wavelets were determined based on the incident laser flux and the Fresnel reflections of the interfaces in the grating while accounting for interference. A depiction of the model used for calculating the flux of the newly created diffraction peaks in this thesis is shown in Figure B-4. Interdigitated ITO films (n2) on glass (n1), immersed in an electrolyte solution comprised of methylene blue dye ions in water (n4), create a diffraction grating. Light reflecting from these interfaces was found by summing up the wavelets along the interface of glass/ITO and glass/MB-H2O. When a potential was applied between the two interdigitated electrodes, the complex index of refraction surrounding one of the two electrodes was changed (n3), and a new diffraction peak was created. The estimated radiant flux that one would expect to experimentally measure for these new diffraction peaks can be found if one 151 accounts for four wavelet groups (although two of the groups are essentially identical). A schematic of these groups is shown in Figure B-4. w n1 n2 n3 n4 2d Figure B-4: The diffraction grating plane composed of four groups of wavelets The radiant flux from these four groups is: 2 𝑤 𝑑 𝑑+𝑤 2𝑑 2𝜋𝑚𝑥 2𝜋𝑚𝑥 2𝜋𝑚𝑥 2𝜋𝑚𝑥 𝐸𝑜 𝑅𝑚 = | (𝑅1∗ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑅2∗ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑅3∗ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 + 𝑅4∗ ∫ 𝑒 𝑖( 𝑑 ) 𝑑𝑥 )| 2𝑑 0 𝑤 𝑑 𝑑+𝑤 𝑅𝑚 = | 2𝜋𝑚𝑤 2𝜋𝑚·𝑤 2𝜋𝑚𝑤 𝐸𝑜 (𝑅1∗ (𝑒 𝑖( 𝑑 ) − 1) + 𝑅2∗ (𝑒 𝑖(2𝜋𝑚) − 𝑒 𝑖( 𝑑 ) ) + 𝑅3∗ (𝑒 𝑖(2𝜋𝑚) 𝑒 𝑖( 𝑑 ) − 𝑒 𝑖(2𝜋𝑚) ) 4𝜋𝑚𝑖 + 𝑅4∗ (1 − 𝑒 𝑖(2𝜋𝑚) 𝑒 𝑖( 2 2𝜋𝑚𝑤 ) 𝑑 ))| (𝑚 ≠ 0) If m is an integer, this equation simply becomes 𝑅𝑚 = | 2 2𝜋𝑚𝑤 𝐸𝑜 (𝑒 𝑖( 𝑑 ) − 1) (𝑅1∗ + 𝑅3∗ − 𝑅2∗ − 𝑅4∗ )| (𝑚 ≠ 0) 4𝜋𝑚𝑖 If 𝑅1∗ =𝑅3∗ , and 𝑅2∗ =𝑅4∗ , then this equation is equivalent to the previous electric field equation, exactly as it should be. Since the diffraction grating pitch has effectively doubled from d to 2d, it is now valid for m to have half-integer values (one could equivalently redefine d to be twice as large, and then the newly created diffraction peak would correspond to m=1). If m is a half-integer, the equation changes to: 2𝜋𝑚𝑤 2𝜋𝑚·𝑤 2𝜋𝑚𝑤 2𝜋𝑚𝑤 𝐸𝑜 𝑅𝑚 = | (𝑅1∗ (𝑒 𝑖( 𝑑 ) − 1) + 𝑅2∗ (−1 − 𝑒 𝑖( 𝑑 ) ) + 𝑅3∗ (−𝑒 𝑖( 𝑑 ) + 1) + 𝑅4∗ (1 + 𝑒 𝑖( 𝑑 ) ))| 4𝜋𝑚𝑖 2 152 2 𝑅𝑚 = | 2𝜋𝑚𝑤 2𝜋𝑚·𝑤 𝐸𝑜 ((𝑒 𝑖( 𝑑 ) − 1) (𝑅1∗ − 𝑅3∗ ) − (1 + 𝑒 𝑖( 𝑑 ) ) (𝑅2∗ − 𝑅4∗ ))| 4𝜋𝑚𝑖 𝜋𝑚𝑤 𝐸𝑜 𝑒 𝑖( 𝑑 𝑅𝑚 = | 4𝜋𝑚𝑖 2 ) ((𝑒 𝑖( 𝜋𝑚𝑤 ) 𝑑 𝜋𝑚𝑤 𝐸𝑜 𝑒 𝑖( 𝑑 𝑅𝑚 = | 2𝜋𝑚 𝑅𝑚 = ) −𝑒 −𝑖( 𝜋𝑚𝑤 ) 𝑑 ) (𝑅1∗ − 𝑅3∗ ) − (𝑒 −𝑖( 𝜋𝑚𝑤 ) 𝑑 + 𝜋𝑚𝑤 𝑒 𝑖( 𝑑 ) ) (𝑅2∗ − 𝑅4∗ ))| 2 𝜋𝑚𝑤 𝜋𝑚𝑤 (𝑠𝑖𝑛 ( ) (𝑅1∗ − 𝑅3∗ ) + 𝑖 𝑐𝑜𝑠 ( ) (𝑅2∗ − 𝑅4∗ ))| 𝑑 𝑑 |𝐸𝑜 |2 𝜋𝑚𝑤 𝜋𝑚𝑤 (𝑠𝑖𝑛2 ( ) |𝑅1∗ − 𝑅3∗ |2 − 𝑐𝑜𝑠 2 ( ) |𝑅2∗ − 𝑅4∗ |2 ) 4(𝜋𝑚)2 𝑑 𝑑 For the diffraction gratings modeled in this thesis, 𝑅2∗ =𝑅4∗ , so the equation can be simplified further: 𝑅𝑚 = |𝐸𝑜 |2 𝜋𝑚𝑤 𝑠𝑖𝑛2 ( ) |𝑅1∗ − 𝑅3∗ |2 2 4(𝜋𝑚) 𝑑 In summary: 𝑚=0 𝑚 = 1, 2, 3, … 𝑚= 1 3 5 , , ,… 2 2 2 |𝐸𝑜 |2 𝑤 𝑑−𝑤 2 |(𝑅1∗ + 𝑅3∗ ) + 2𝑅2∗ | 2 𝑑 𝑑 |𝐸𝑜 |2 𝜋𝑚𝑤 𝑅𝑚 = 𝑠𝑖𝑛2 ( ) |(𝑅1∗ + 𝑅3∗ − 2𝑅2∗ )|2 2 4(𝜋𝑚) 𝑑 |𝐸𝑜 |2 𝜋𝑚𝑤 𝑅𝑚 = 𝑠𝑖𝑛2 ( ) |𝑅1∗ − 𝑅3∗ |2 4(𝜋𝑚)2 𝑑 𝑅0 = The only remaining values to determine are the complex reflection coefficients from each point source group, 𝑅1∗ →𝑅4∗ . These numbers represent the amplitude and phase of each of the four point source groups. Determining these values requires accounting for Fresnel reflections and the interference of waves from one or more thin films. Interference When a wave strikes an interface between two materials of two different indices of refraction, a portion of the wave is reflected, transmitted, and sometimes a portion is absorbed. Often the reflection or transmission of these waves is calculated in terms of the portion of the incident flux that is reflected and transmitted, but in order to take interference into account, one must find the electric field amplitude reflectance and transmission values. 153 Figure B-5: Reflection and transmission of the electric field The reflection at an interface is simply the Fresnel coefficient multiplied by the incident electric field amplitude. For the case of s-polarized light, which was the type of light used for the experiments described in this thesis, the Fresnel coefficient can be found from equation (14). In this thesis, the light in one of the mediums was an evanescent wave, and hence it became necessary to account for the reflection of an evanescent wave at an interface. Using the equation given above, this seems impossible as there is no meaningful value of 𝜃𝑖 . However, the equation can be written in terms of the angle in a previous medium, 𝜃𝑝 , with index np at which the light was not evanescent. This equivalent form of the Fresnel coefficient is written in the following way: 𝑛1 √1 − ( 2 2 𝑛p 𝑛p sin 𝜃𝑝 ) − 𝑛2 √1 − ( sin 𝜃𝑝 ) 𝑛1 𝑛2 𝑛1 √1 − ( 2 2 𝑛p 𝑛p sin 𝜃𝑝 ) + 𝑛2 √1 − ( sin 𝜃𝑝 ) 𝑛1 𝑛2 𝑟𝑠 = 154 Figure B-6: Multiple reflections and transmissions of the electric field For the case of a thin film, multiple reflections and transmissions must be taken into account in order to determine the net reflected and transmitted electric field amplitudes. The resulting reflected electric field amplitude is the result of an infinite series of interfering waves. ∞ 𝐸𝑅 = 𝑅∗ = 𝑟1 + (1 − 𝑟12 ) · 𝑟2 · ∑ (−𝑟1 𝑟2 )𝑚 𝑒 𝑖(𝑚+1) · 𝜙 𝐸𝑜 𝑚=0 𝑅∗ = 𝑟1 + 𝑟2 𝑒 𝑖𝜙 1 + 𝑟1 𝑟2 𝑒 𝑖𝜙 The transmitted wave can similarly be calculated ∞ 𝐸𝑇 = 𝑇 ∗ = √1 − 𝑟12 √1 − 𝑟22 ∑ (−𝑟1 𝑟2 )𝑚 𝑒 𝑖𝑚𝜙 𝐸𝑜 𝑚=0 𝑇∗ = √1 − 𝑟12 √1 − 𝑟22 1 + 𝑟1 𝑟2 𝑒 𝑖𝜙 For the case of two thin films, the resulting electric field amplitude is: 𝑅∗ = 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙2 + 𝑟1,2 𝑟2,3 𝑟3,4 𝑒 𝑖𝜙3 + 𝑟3,4 𝑒 𝑖(𝜙2 +𝜙3 ) 1 + 𝑟1,2 𝑟2,3 𝑒 𝑖𝜙2 + 𝑟2,3 𝑟3,4 𝑒 𝑖𝜙3 + 𝑟1,2 𝑟3,4 𝑒 𝑖(𝜙2 +𝜙3 ) 155 These equations require a separate calculation of the Fresnel coefficient at each interface and the optical path differences (OPD) through each thin film (𝜙2 and 𝜙3 ). The optical path difference can be found in the standard way. Figure B-7: Optical path difference 𝑂𝑃𝐷 = 2𝑛2 𝐵 − 𝑛1 𝐴 = 2𝑛2 𝑑 − 𝑛1 2𝑡 · 𝑆𝑖𝑛(𝜃1 )𝑇𝑎𝑛(𝜃2 ) 𝐶𝑜𝑠(𝜃2 ) = 2𝑛2 𝑡 · ( 1 𝑆𝑖𝑛(𝜃2 )2 − ) 𝐶𝑜𝑠(𝜃2 ) 𝐶𝑜𝑠(𝜃2 ) = 2𝑛2 𝑡 · 𝐶𝑜𝑠(𝜃2 ) The phase difference associated with the optical path difference is then: 𝜙 = 𝑂𝑃𝐷 · 2𝜋 𝜆 = 2𝑛2 𝑡 · 𝐶𝑜𝑠(𝜃2 ) · = 2𝜋 𝜆 4𝜋𝑡 √𝑛22 − 𝑛12 sin2 (𝜃1 ) 𝜆 Finally, with these equations the expected diffraction peak flux values can be calculated. Diffraction Peak Radiant Flux Calculations Finally, after incorporating the effect of thin film interference and the results from the previous section, the ratio of the experimentally measured diffraction peak flux values to the incident laser flux (the flux fraction) were calculated. For the first case the flux fraction of the 156 first few diffraction peaks was calculated when no potential was applied between the interdigitated electrodes. In this case, there were two major wavelet regions, the first arising from the ITO/glass interface, and the second arising from the glass/MB-H2O interface. The complex Fresnel coefficients will be written in terms of an interface. For example, the Fresnel coefficient for the interface of mediums 1 and 2 will be written as 𝑟1,2. Figure B-8: Single pitch of diffraction grating Using this notation, the resulting reflected flux fractions for the 0th order and higher order diffraction peaks are then: 2 𝑅0 = |𝐸𝑜 |2 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙 𝑤 𝑑−𝑤 |( ) + 𝑟1,3 | 𝑖𝜙 1 + 𝑟1,2 𝑟2,3 𝑒 𝑑 𝑑 |𝐸𝑜 |2 𝜋𝑚𝑤 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙 2 𝑅𝑚 = sin ( ) |( ) − 𝑟1,3 | (𝜋𝑚)2 𝑑 1 + 𝑟1,2 𝑟2,3 𝑒 𝑖𝜙 𝜙= 2 4𝜋 · 𝑡 √𝑛22 − 𝑛12 sin2 (𝜃1 ) 𝜆 When a potential is applied between the interdigitated electrodes, a layer of increased methylene blue ionic concentration is created around one of the electrodes. In this case the diffraction peaks are calculated based on four wavelet groups. 157 Figure B-9: Diffraction grating pitch for new diffraction peaks 2 𝑚=0 |𝐸𝑜 |2 𝑟1,2 + 𝑟2,4 𝑒 𝑖𝜙2 + 𝑟1,2 𝑟2,4 𝑟4,3 𝑒 𝑖𝜙4 + 𝑟4,3 𝑒 𝑖(𝜙2+𝜙4 ) 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙2 𝑤 𝑑−𝑤 𝑅0 = |( + ) + 2𝑟1,3 | ) 𝑖𝜙 𝑖𝜙 𝑖𝜙 𝑖(𝜙 +𝜙 2 2 4 2 4 2 1 + 𝑟 𝑟 𝑒 𝑑 𝑑 1 + 𝑟1,2 𝑟2,4 𝑒 + 𝑟2,4 𝑟4,3 𝑒 + 𝑟1,2 𝑟4,3 𝑒 1,2 2,3 𝑚 = 1, 2, 3, … |𝐸𝑜 |2 𝜋𝑚𝑤 𝑟1,2 + 𝑟2,4 𝑒 𝑖𝜙2 + 𝑟1,2 𝑟2,4 𝑟4,3 𝑒 𝑖𝜙4 + 𝑟4,3 𝑒 𝑖(𝜙2 +𝜙4 ) 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙2 2 𝑅𝑚 = 𝑠𝑖𝑛 ( ) | + − 2𝑟1,3 | 4(𝜋𝑚)2 𝑑 1 + 𝑟1,2 𝑟2,4 𝑒 𝑖𝜙2 + 𝑟2,4 𝑟4,3 𝑒 𝑖𝜙4 + 𝑟1,2 𝑟4,3 𝑒 𝑖(𝜙2 +𝜙4 ) 1 + 𝑟1,2 𝑟2,3 𝑒 𝑖𝜙2 1 3 5 𝑚 = , , ,… 2 2 2 |𝐸𝑜 |2 𝜋𝑚𝑤 𝑟1,2 + 𝑟2,4 𝑒 𝑖𝜙2 + 𝑟1,2 𝑟2,4 𝑟4,3 𝑒 𝑖𝜙4 + 𝑟4,3 𝑒 𝑖(𝜙2 +𝜙4 ) 𝑟1,2 + 𝑟2,3 𝑒 𝑖𝜙2 2 𝑅𝑚 = 𝑠𝑖𝑛 ( ) | − | 4(𝜋𝑚)2 𝑑 1 + 𝑟1,2 𝑟2,4 𝑒 𝑖𝜙2 + 𝑟2,4 𝑟4,3 𝑒 𝑖𝜙4 + 𝑟1,2 𝑟4,3 𝑒 𝑖(𝜙2+𝜙4) 1 + 𝑟1,2 𝑟2,3 𝑒 𝑖𝜙2 2 𝜙2 = 4𝜋 · 𝑡2 √𝑛22 − 𝑛12 sin2 𝜃1 𝜆 𝜙4 = 4𝜋 · 𝑡4 √𝑛42 − 𝑛12 sin2 𝜃1 𝜆 These are the final equations used to calculate the new diffraction peak radiant flux fraction values. 158 2















































































































































































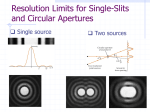



![Scalar Diffraction Theory and Basic Fourier Optics [Hecht 10.2.410.2.6, 10.2.8, 11.211.3 or Fowles Ch. 5]](http://s1.studyres.com/store/data/008906603_1-55857b6efe7c28604e1ff5a68faa71b2-150x150.png)



