Download Interfacing single photons and condensed

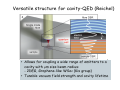
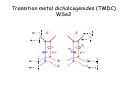
Interfacing single photons and
condensed-matter systems
A. Imamoglu
Quantum Photonics Group, Department of Physics
ETH‐Zürich
Outline
• A two dimensional electron gas embedded in a
microcavity at B=0: Fermi-edge polaritons?
• Strong coupling of optical excitations out of
quantum Hall ground states to a microcavity.
Outline
• A two dimensional electron gas embedded in a
microcavity at B=0: Fermi-edge polaritons?
• Strong coupling of optical excitations out of
quantum Hall ground states to a microcavity.
Motivation
• A new spectroscopic tool for studying
condensed-matter; bulk properties, quantum
quenches, etc.
• A new paradigm for quantum optics with
nonlinearities arising from correlations.
Coupling optical excitations of 2D semiconductors to cavities
Undoped QW
Exciton
resonance
A bound electron‐hole pair free to move in 2D
Coupling optical excitations of 2D semiconductors to cavities
Undoped QW
Exciton
resonance
A bound electron‐hole pair free to move in 2D
Undoped QW in a cavity: polaritons
Strong‐coupling regime: two split harmonic oscillator modes for each in‐plane k (Bloch)
Coupling optical excitations of 2D semiconductors to cavities
Undoped QW
Exciton
resonance
Undoped QW in a cavity: polaritons
2D electron gas
Fermi edge Singularity
(FES)
Electrons at the Fermi‐
surface of the 2DEG screen out the (heavy) hole/impurity potential and in the process render the final state Fermi sea wave‐funtion orthogonal to the initial one:
Power‐law tails
Coupling optical excitations of 2D semiconductors to cavities
Undoped QW
Exciton
resonance
Undoped QW in a cavity: polaritons
2DEG
Fermi edge Singularity
(FES)
Electrons at the Fermi‐
surface of the 2DEG screen out the (heavy) hole/impurity potential and in the process render the final state Fermi sea wave‐funtion orthogonal to the initial one:
Power‐law tails
2DEG in a cavity: Fermi‐edge polaritons
Theoretical prediction by Averkiev & Glazov (2007): ignores finite hole mass and assumes power law is not altered by the strong cavity coupling
Experiment: a gate-tunable 2DEG
embedded in a DBR microcavity
• The experiments are carried out in a fiber-coupled dil
fridge at an electron temperature of T~200 mK
Electron density is varied from 3x1010 to about
3x1011 covering the ranges kFaB < 1 & kFaB > 1
Density dependent optical spectrum
• Low electron density: trions
and excitons are simultaneously
visible; PL from trion – the
lowest energy excitation
• Medium density: exciton
disappeares. Trion aquires an
asymmetric lineshape (FES).
• High density; PL from the
whole Fermi sea is visible.
Asymmetric reflection/
absorption at the Fermi level
Low density limit: tuning the cavity
through the QW resonances
High density limit: tuning the
cavity through the Fermi edge
The excess broadening of the cavity‐mode for Ecav
> EF is consistent with per pass absorption of %
High electron density regime:
cavity on resonance with the Fermi edge
• As the temperature is lowered below 4K, a split resonance
with large asymmetry and a sharp lower peak appears
• The lower energy peak is ~lorentzian and is narrower than
the cavity-mode.
T = 4K
T = 0.2K
High electron density regime:
cavity on resonance with the Fermi edge
• As the temperature is lowered below 4K, a split resonance
with large asymmetry and a sharp lower peak appears
• The lower energy peak is ~lorentzian and is narrower than
the cavity-mode.
• «Best fit» with Glazov model
yields an exponent of -0.7!
T = 0.2K
Fermi-edge polaritons
• Dispersion relation could be measured using
white-light reflection at a finite angle
• The splitting g > κcav/2 – strong coupling!
Fermi‐edge polaritons as the denisty is increased above kFaB > 1
ne increased from 1x1011 (black) to 3x1011 (red)
Features and open questions
• The role of hole-recoil: the disappearance of normal
mode splitting with increasing electron density (kF)?
• We expect recoil to change the low energy physics
and to remove the enhancement of the optical
coupling at the Fermi edge – why does the narrow
lower-polariton peak survive?
• Note: interesting physics takes place in the final
state of the optical transition
Two-dimensional electron-gas (2DEG)
in a perpendicular magnetic field
• A Hall bar of size 1 mm and an optical excitation spot of
2 μm diameter, probing the bulk locally.
Transport measurements
Landau levels in off‐resonant cavity reflection
ν1
ν=1
Cavity
• Landau fan of singlet trion lines
• Spin polarization at n=1 is visible
• For B > 4 T, exciton line also appears
ν=1
Polariton modes for 2 > ν > 1 at B= 3T
ν = 1
ν = 2
ν = 2
•
•
•
For ν > 2, we observe the uncoupled cavity reflection since all electronic transitions are Pauli‐blocked
At ν = 2, a normal mode splitting appears
At ν = 1, ‐ splitting is minimal whereas + splitting is maximal.
Polariton modes at ν = 1 (B=3T)
Spin polarization at ν=1 is not perfect: high temperature or heavy‐
light‐hole mixing?
Polariton modes at B=6T
• ν = 1 spin polarization occurs over a very narrow gate voltage range
• No feature at ν = 2/3 (spin polarization or depolarization)
• A small feature at ν = ½
• The cavity is red‐detuned – hence the asymmetry of the polariton peak strengths.
Few-photon dependent reversible
polariton splitting
Line cut at 4T without (red) and with (blue) a resonant laser.
Time‐resolved measurents:
laser power on sample 60pW
• Controlling polariton splitting with single photons: strong photon‐photon interactions?
Features and open questions
• Cavity-QED is a powerful spectroscopic tool for
studying the bulk properties of both IQHE and
FQHE states:
-
-
The optically generated hole is delocalized over
the entire excitation region.
Spectroscopy using one photon at a time – photon
absorption induced local heating can be minimized
(signal = transmission/reflection of incident
photons).
Sensitivity of the polariton splitting to
incompressibility of the ground-state?
• Novel platform for photon-photon interactions
• Photon absorption induced quantum quench into
or out of a state with topological order?
Versatile structure for cavity-QED (Reichel)
• Allows for coupling a wide range of emitters to a
cavity with m size beam radius:
- 2DEG, Graphene-like WSe2 (Kis group)
• Tunable vacuum field strength and cavity lifetime
Transition metal dichalcogenides (TMDC)
WSe2
m=+3/2
m=+1/2
m=‐3/2
m=‐1/2
m=+1/2
m=‐1/2
m=‐1/2
m=+1/2
Photoluminescence from a monolayer of WSe2
Degree of circular dichroism: ~ 50 – 60 %
quantum dot?
Measurement of the exciton magnetic moment: Faraday geometry
~ 2.5meV@ 8T
g‐factor ~5
‐linearly polarized excitation
‐detection in circular basis Measurement of the exciton magnetic moment: Faraday geometry
~ 2.5meV@ 8T
g‐factor ~5
‐linearly polarized excitation
‐detection in circular basis Voigt geometry
Strongly anisotropic magnetic field response – consistent with the orbital contribution.
Thanks to
• Stephan Smolka, Wolf Wuester, Werner Wegscheider
• Ajit Srivastava, Meinrad Sidler, Andras Kis