Download The Sky

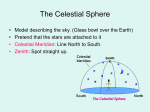
Astronomy 291
Professor Bradley M. Peterson
The Sky
• As a first step, we need to understand the
appearance of the sky.
• Important points (to be explained):
– The relative positions of stars remain the same
(on human time scales).
– The Sun moves eastward relative to the stars
(about 1° per day).
• Relative to the Sun, stars rise 4 min earlier each day.
– The Moon moves eastward relative to the stars
(about 13° per day).
2
The Celestial Sphere
• To understand the
appearance of the sky,
it is useful to imagine
it as a sphere with
Earth at the center.
• Observer can see only
sky above the horizon
(an imaginary plane
tangent to Earth at the
observer).
Observer
3
The Celestial Sphere
• Suppose Earth is
stationary; then sky
revolves around axis
that is extension of the
Earth’s rotation axis.
• Rotation axis intersects
celestial sphere at north
and south celestial
poles.
4
The Celestial Sphere
• Rotation of the sky is
apparently westward as
seen by the observer.
• Stars near celestial pole
never drop below
horizon. These are
circumpolar stars.
5
North Circumpolar Stars in Time Exposure
6
The Celestial Sphere
• Rotation of the sky is
apparently westward as
seen by the observer.
• Stars near celestial pole
never drop below
horizon. These are
circumpolar stars.
Now let’s expand the
view of the Earth
in this diagram….
7
Projection of equator on to sky is the celestial equator.
8
The zenith is the point on the celestial sphere directly
above the observer.
9
The meridian passes through the celestial poles and
the zenith, bisecting the sky into east and west.
10
Apparent Paths
of Stars
• To see the motion of
the stars, let’s zoom
back outside the
celestial sphere….
11
Apparent Paths
of Stars
• During the course of
the day, stars move in
circles at a fixed
distance from the
celestial equator.
• This diurnal motion is
really due to the
rotation of the Earth,
not the sky.
12
From mid-northern
latitudes:
Vega passes
nearly overhead
Mizar is a
circumpolar star
All stars north
of the celestial
equator are above
the horizon more
than 12 hours
Southern stars are
above the horizon
less than 12 hours
Stars on the celestial equator
are above the horizon exactly
12 hours every day
13
Motion of the Sun
• The Sun also appears to rise in the east and
set in the west due to the Earth’s rotation.
• However, the Sun moves relative to the
stars:
– The Sun moves eastward relative to the stars by
about 1° per day.
– The Sun oscillates north/south (within 23°.5 of
the celestial equator) over a period of one year.
14
Sun’s Motion in the Sky
North
Sun moves 1°/day
along the
ecliptic
East
West
celestial equator
ecliptic
South
15
Sun’s Motion in the Sky
North
Vernal equinox
(first day of Spring)
East
West
celestial equator
ecliptic
South
16
Sun’s Motion in the Sky
North
Summer solstice
(first day of Summer)
East
West
celestial equator
ecliptic
South
17
Sun’s Motion in the Sky
North
Autumnal equinox
(first day of Autumn)
East
West
celestial equator
ecliptic
South
18
Sun’s Motion in the Sky
North
Winter solstice
(first day of Winter)
East
West
celestial equator
ecliptic
South
19
The Ecliptic
• The ecliptic is the
Sun’s path among
the stars.
• It is simply the
projection of the
Earth’s orbital
plane onto the
celestial sphere.
September
November
c
i
t
p
i
Ecl
July
April
January
20
Diurnal Path
of the Sun
• The Sun’s diurnal
path varies during
the year.
• Time above
horizon depends on
where it is relative
to the celestial
equator.
21
Equinoxes
9 am
• Equinoxes occur
when the Sun
crosses the equator
(about 21 March
and 21 September).
• Days and nights
have equal length,
exactly 12 hours.
noon
6 am
6 pm
midnight
22
Solstices
• Dates known as the
solstices occur
when Sun is
farthest from the
celestial equator.
Summer solstice (about
21 June)
noon
6 am
4 am
6 pm
8 pm
23
Solstices
• Dates known as the
solstices occur
when Sun is
farthest from the
celestial equator.
noon
8 am
6 am
4 pm
Winter solstice (about
21 December)
6 pm
24
The Zodiac
Apparent eastward
motion of Sun
March
June
• The Sun’s
motion on the
ecliptic carries it
through a group
of constellations
called the
zodiac.
25
Measurement of Time
• Study of astronomy originally motivated by
need for accurate calendars.
• Calendars are necessary for successful
agriculture.
26
Seasonal
Variations
• Seasonal variations in
temperature are due to
two factors:
– Amount of time Sun
spends above horizon
– Maximum elevation of
Sun in sky
27
Basic Measures of Time
Measure
Day
Month
Year
Phenomenon
Rotation of the Earth
Revolution of the Moon
Revolution of the Earth
Day, month, and year are of
astronomical origin.
28
Prehistoric Astronomy
• The week is also tied to astronomy:
– Weeks are an invention of the Babylonians,
loosely based on quarter of lunar cycle.
– Number of days in week equals number of
“planets” (non-stationary celestial objects)
– Seven objects in the sky move relative to the
stars: Sun, Moon, Mercury, Venus, Mars,
Jupiter, and Saturn. English names for the days
of the week are based on these.
29
Names of the Days of the Week
Day (English)
Teutonic God
(equivalent)
“Planet”
Day (French/Italian)
Sunday
Sun
dimanche/domenica
Monday
Moon
lundi/lunedi
Tuesday
Tiw
Mars
mardi/martedi
Wednesday
Woden
Mercury
mercredi/mercoledi
Thursday
Thor
Jupiter
jeudi/giovedi
Friday
Frigg
Venus
vendredi/venerdi
Saturn
samedi/sabato
Saturday
30
Motions of the Earth and
Measures of Time
• The major motions of the Earth determine
how we measure time
– Rotation
• days, hours, minutes, seconds
– Revolution and Precession
• years
31
Motions of the Earth
1 Rotation (P = 23h 56m)
– Earth rotates eastward (i.e., west to east) on its
axis.
• Solar Day = 24h 00m
• Sidereal Day = 23h 56m
32
Rotation of the Earth
Sidereal Day
Solar Day
Earth
1°
one day
later
23h 56m
24h 00m
Sidereal day: one full rotation with respect to the stars.
Solar day: one full rotation with respect to the Sun.
33
Rotation of the Earth
• It takes the Earth about 4 minutes to rotate
the extra 1°.
• Because of difference in sidereal and solar
time, stars rise 4 minutes earlier each day.
34
Rotation of the Earth
• Proof of rotation: The
Foucault Pendulum
– A large mass
suspended by a wire
oscillates in a single
plane (Newton’s First
Law).
– The Earth rotates
underneath the
Foucault Pendulum
35
Major Motions of the Earth
1 Rotation (P = 23h 56m )
2 Revolution (P = 1 year)
– The Earth revolves around the Sun,
counterclockwise as seen from above the North
Pole.
36
Revolution of the Earth
• Proof of revolution: Stellar parallax
• Parallax is the apparent motion of nearby
stars due to the motion of the Earth around
the Sun.
37
Stellar Parallax
• Apparent motion of nearby stars
Earth three months later
"
1 AU
Star
Earth
Sun
Parallax angle "
38
39
Stellar Parallax
• Parallax is inversely proportional to
distance: = 1/ d
• Largest observed parallax is for  Centauri
–  = 0.75 arcseconds
– d = 4 ×1016 m = 270,000 AU
• Because stellar parallaxes are so small, they
were not measured until 1838.
40
Precession
Equator
Earth’s rotation
axis
Ecliptic
41
Precession
• Sun and Moon pull Earth’s equatorial
bulges towards ecliptic
• This results in westward precession of the
Earth’s rotation axis
42
Precession
• The line of intersection of the ecliptic and
celestial equator also precesses westward.
• Precession causes the vernal equinox to
move westward.
• This makes the calendar year (called the
tropical year) shorter than the sidereal (or
orbital) year.
43
Tropical Year
One tropical year
Vernal equinox 2000
Motion of the
Equinoxes

Vernal equinox 1999
Sun
Direction of
Earth’s Motion
44
Tropical Year
Tropical Year:
365.242191 days

Sidereal Year:
365.256363 days
Sun
45
Period of Precession
• Sidereal year: 365d.256363
• Tropical year: 365d.242191
• Difference:
0d.0142 = 20m 24s.5
days
d
0.0142
 N (years)  365 .256
year
N  25,772 years
46
Time and Calendars
• Civil time: Based on the solar day (defined
by successive transits of the Sun)
• Though Earth’s rotation speed remains
(nearly) constant, length of solar day is
variable.
47
Time and Calendars
• Why is the length of the solar day variable?
1 Tilt of the Earth’s axis (astronomers call this
the “obliquity of the ecliptic”)
48
Obliquity of the Ecliptic
Solstice
N
+20º
Equator
W
-20º
Equinox
Ecliptic
12h
6h
0h
18h
12h
49
Qbliquity of the Ecliptic
• Motion of the Sun along the equator is
greater at solstice than at equinox; length of
the solar day is longer at solstice.
50
Time and Calendars
• Why is the length of the solar day variable?
1 Tilt of the Earth’s axis (astronomers call this
the “obliquity of the ecliptic”)
2 Eccentricity of the Earth’s orbit (Kepler’s
Second Law)
51
Eccentricity of the Earth’s Orbit
Solar Day
Sidereal Day
52
Eccentricity of the Earth’s Orbit
Sidereal Day
Solar Day
53
Eccentricity of Earth’s Orbit
• Solar days are thus longest at perihelion
since the Earth must rotate farther to catch
up with the rapid rate at which the Sun is
moving across the sky (i.e., the rapid rate
the Earth is moving in its orbit).
54
Time and Calendars
• Mean Solar Time (MST): based on the
apparent motion of the Sun over a year.
This is what clocks measure; it moves at a
fixed rate.
• The Sun actually moves at a variable rate;
time kept by the real Sun is called apparent
solar time.
55
Equation of Time
• Apparent Solar Time is where the Sun is in
the sky (time measured by sundials).
• The difference between MST and Apparent
Solar Time is the Equation of Time.
MST +
Equation =
of Time
Apparent
Solar Time
56
Equation of Time
• Apparent Solar Time and Mean Solar Time
can differ by as much as 16 minutes.
MST +
Equation =
of Time
Apparent
Solar Time
57
True Sun Behind
58
True Sun Ahead
Equation of Time
59
Equation of Time
• We can also plot the Sun’s declination
(angle from the celestial equator) versus the
equation of time.
• This gives a shape called the analemma.
60
The Analemma
This is often found on
globes.
June
Aug
Declination
The analemma shows the
equation of time and
declination of the Sun.
Mar
May
Sep
Nov
Jan
Time (min)
61
The Analemma
• If you take a photograph at the same (mean
solar) time each day, you can see how the
Sun moves in declination and when it is
ahead and behind of the mean Sun.
62
63
Time Conventions
• Civil Time = Mean Solar Time in year 1900
A.D.
– Earth’s rotation is slowing down, so Earth runs
slower than clocks.
– Compensate by periodically adding leap
seconds, which let the Earth catch up to clocks.
– About 29 leap seconds have been added
between 1900 and 2000.
64
How’s the Math on That Figure?
• A day in the year 2000 is longer than a day
in the year 1900 by 0.0016 seconds.
• The average day in the 20th Century is thus
longer than a day in the year 1900 by half
this, 0.0016/2 =0.0008 seconds.
• Earth falls behind clocks by this amount
every day, for all 36525 days of the century.
• 0.0008 seconds/day × 36525 days = 29 sec.
65
Calendars
• The difficulty with calendars is that the
tropical year is not an integral number of
solar days.
• We therefore use tropical years with a
variable number of integral days to
approximate the true tropical year.
66
Early Roman Calendar
Day 730
Day 365
Day 0

Early Roman calendar of 365 days per year was too short.
First day of Spring occurred later each year.
67
Early Roman Calendar
• 1 year = 365 days
• Vernal equinox occurs later each year.
• After only 128 years, vernal equinox has
moved from March 21 to April 21.
68
Julian Calendar
• Add an extra day every fourth year:
–
–
–
–
Year 1: 365 days
Year 2: 365 days
Year 3: 365 days
Year 4: 366 days
• Average length of year: 365.25 days
69
Julian Calendar
• But after 100 years, the Julian calendar is in
error by more than 3/4 day.
– After 100 years:
100 tropical
 (75 years+25 leap years)
Difference
36524.2191
 36525
 0.7809
70
Gregorian Calendar
• The Julian Calendar has overcorrected by
3/4 of a day, so skip a leap year every
century (1800, 1900, etc.).
400 tropical
146,096.876
 (304 regular years +  146,096.000
96 leap years)
Difference
+0.876
71
Gregorian Calendar
• But skipping a leap year every 100 years
leads to an error of near one day after 400
years.
• Add an extra leap year every 400 years
(instead of skipping the leap year in century
years). Thus, 1200, 1600, 2000, and 2400
are leap years, not skipped leap years.
72
Gregorian Calender
• 365 days per year (Early Roman)
• Years divisible by 4 are leap years, and
have 366 days (Julian modification)
– If year is also divisible by 100, skip the leap
year and make it a regular year
• If year is also divisible by 400, then don’t skip the
leap year, keep it! (Gregorian modifications)
• One day error accumulates after 3225 years
73
Chapter 2: Emergence of Modern
Astronomy
74