Download Black-Body SNR Formulation of Astronomical Camera

1
Black-Body SNR Formulation of Astronomical Camera
Systems
Engin Tola
Abstract—In this study, we present a formulation for the computation of the SNR of an image system designed for astronomical star
observations by combining research results from different disciplines such as physics, astronomy, optics and electronics. Starting from
the energy emitted by the stars and their catalogued magnitudes, we formulate the amount of electrons formed in the pixels of an image
sensor using the camera parameters and then compute the quality of the signal in terms of SNR. We provide formulations for both
space bound and earth bound observations of stars and present example numerical data for a camera and a telescope system. The
formulation given here, although not novel if considered separately in its components, combines the information of different disciplines
in an effort to present a complete resource that relates the full image chain from the source to the finally formed image in the hope that
it will be a self-contained reference for other researchers working on astronomical camera systems.
Index Terms—SNR, stellar flux, apparent magnitude, black-body radiation, astronomical observation, photon counts, telescope design
F
1
I NTRODUCTION
A
N electro-optical system has many interacting parameters
that effect the quality of the formed image in different
ways. For example, decreasing the f-number of the optical
system by increasing the aperture diameter causes more light
to enter the camera and this will likely improve the SNR but it
also results in an increase in the size and weight of the whole
system which might be undesirable; moreover, it typically
decreases the optical performance because of an increase of
the aberations. It follows that it is not possible to build an
optimal camera that can be used for all situations and therefore,
it is common practice to build camera systems considering
the requirements of the capturing purpose. This, however,
necessitates to understand the relations of different parameters
of the system in order to have an estimate about the quality of
the image that will be achieved from a proposed design. In this
work, we will be considering astronomical imaging systems
for star observations, i.e. our objects of interests are point light
sources. For more general simulations refer to the image chain
simulation literature [1].
Our main purpose in this study is to relate the capture
quality of an image system to a star’s astronomical and
physical properties. More specifically, for a given imaging
system, we would like to model the relationship between a
star’s catalogued brightness value to the SNR that it will be
observed with. For this purpose, we will first describe how to
estimate the incoming flux from a star of known brightness in
Section 2, present our camera model in Section 3, delineate
the various sources of noise in an image in Section 4 and
then formulate the amount of signal formed on the image
sensor and its SNR in terms of camera parameters in Section 5.
Finally, simulation results for two different camera systems are
presented in Section 6.
2
F LUX E STIMATION BY B LACK - BODY F ORMULATION
This section details how to estimate the amount of photons
on top of the Earth’s atmosphere coming from a star of known
brightness and temperature. We will construct our formulation
E. Tola is with the Aurvis Research and Development Co., Ankara, Turkiye.
Web : www.aurvis.com
Fig. 1. Spectral plane emittance of a black-body radiator at its
surface at different temperatures.
assuming the stars behave as perfect black-body radiators [2]
and follow the same derivation presented in [3]. Black-body
radiation is the type of electromagnetic radiation emitted by a
body that is in thermal equilibrium at a definite temperature.
The spectral plane emittance from a black-body is given by
Planck’s radiation law [4][5] as:
2πhc2
J
(1)
Bλ (T ) =
2
hc
m ·m·s
λ5 (e λkT − 1)
where, λ is the wavelength, T is the temperature, h is the
Planck’s constant, c is the speed of light in vacuum and
k is the Boltzmann’s constant. The equation formulates the
energy emitted per second per unit area per wavelength from
a surface of absolute temperature T at wavelength λ. Various
universal constants used here are given in Table 1 in SI
units. Figure 1 shows spectral energy distribution estimates
according to black-body models at different temperatures and
Figure 2 shows the fitness of the black-body model to the Sun’s
measured irradiance spectrum [6].
One can convert this emittance to a photon flux by dividing
Equation 1 with the energy of a photon:
Bλ (T )
2πc
photon
φλ (T ) =
=
hc
m2 ·m·s
Ephoton
λ4 (e λkT − 1)
hc
J
with Ephoton =
.
(2)
photon
λ
2
TABLE 1
Constants
c
h
Fig. 2. Sun’s measured irradiance spectrum is compared to
its black-body model. Here, the plotted measurement values
are taken from the ASTM extraterrestrial spectrum reference [6]
and the black-body spectrum is computed using Sun’s effective
temperature (5778 K). Note that Fig. 1 shows the spectrum on
the surface of the Sun. To compute the portion of it that reaches
Earth, according to the r2 -law for irradiance (see Eq. 7), we
2
2
/REarth
(see Table 1).
scale the spectrum with RSun
(a)
(b)
Fig. 3. (Left) Photon ratio for bands 400-625 nm and 400-800
nm at different temperatures (Right) Emitted photon ratio with
different bandwidths at T=10000K
The total number of photons emitted at all wavelengths per
square-meter per second could be calculated by integrating the
photon flux over λ with:
Z ∞
Z ∞
2πc
dλ
(3)
Φ(T ) =
φλ (T ) dλ =
hc
4
λkT
0
0
λ (e
− 1)
hc
Applying the change of variable x = kλT
and reorganizing
the integral results
Z
2πk3 T 3 ∞ x2
Φ(T ) =
dx
(4)
h3 c 2
ex − 1
0
for which the integral evaluates approximately to 2.4041 and
the total photon count equation simplifies to
4.8082 π k3 3
photon
3
Φ(T ) =
T
=
α
T
(5)
2
m ·s
h3 c2
Note that Φ(T ) is the total number of photons at all wavelengths per square-meter per second. Imaging sensors, however, operate only for a limited band. Therefore, to compute
the ratio of the photons in a specific bandwidth, we compute
Z λ1
1
ηT (λ0 , λ1 ) =
φλ (T ) dλ
(6)
Φ(T ) λ0
2.997 · 10
6.626 ·
8
10−34
10−23
k
1.38 ·
α
1.52 · 10
σ
5.67 · 10−8
Lo
3.846 · 1026
Mo
4.83
mo
−26.74
RSun
6.95 · 10
15
m/s
Speed of light
J/s
Planck’s constant
J·K−1
Boltzmann’s constant
photon
K 3 ·m2 ·s
J
K 4 ·m2 ·s
4.8082 π k3
h3 c2
Stefan’s constant
W
Sun’s luminosity
Sun’s absolute magnitude
Sun’s apparent magnitude
8
REarth
1.496 · 10
TSun
5778
11
m
Sun’s equatorial radius
m
Sun’s mean distance
K
Sun’s effective temperature
which could be numerically evaluated. In Figure 3-a we present
the change of the photon ratio computed for different temperatures for the bands 400-625 nm and 400-800 nm. As can be
seen, the peak for these bands is achieved around 10000 K.
We also generated the photon ratio curves, i.e. ηT (λ0 , λ1 ), for
different bands with bandwidths equal to 225, 300 and 400
nm in Figure 3-b at 10000K. From the figure, it is clear that
different bandwidths achieve their peak at different intervals
with a trend that favors smaller starting wavelengths as the
bandwidth increases. This is an important fact to be aware
of when designing detectors to visualize stars with specific
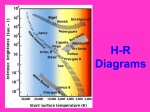
temperature constraints. The Hertzsprung-Russell diagram,
given in Figure 4, shows the relationship between the stars’
luminosity compared to their temperatures and magnitudes. In
Figure 4, we plot the HR diagram for stars with two different
apparent brightness thresholds: mv < 6.5 and mv < 22. The
first limit is to show the trend of the distribution for stars that
can be seen by humans from Earth in a clear night sky. From
this diagram it follows that most stars humans can see from
Earth have temperatures above 5000K (the median is about
6500K). However, the right diagram shows that for stars with
lower brightness values, the temperature is also lower. Hence,
the HR diagram should be consulted to correctly estimate the
photon flux for a desired magnitude range.
The derived photon flux formula given in Eq. 5 is for the
surface of the stars. However, we need to estimate the amount
that reaches Earth. To be able to do that we need to either
know the temperature and distance of the stars that we want
to observe or relate the photon flux of a star to a more readily
available information: its observed brightness. Astronomers have
been observing the stars for thousands of years and have
cataloged the brightness information for many of the stars. A
star’s observed brightness is related to its luminosity (the total
amount of energy emitted per unit time) and its distance to us
by the relation:
L = 4πd2 b,
(7)
where b is its brightness and d is its observation distance. However, instead of dealing with the physical brightness measures
for the stars, astronomers opted to adapt magnitude systems
that are more meaningful with respect to the human visual
system. The brightness systems were developed to reflect the
belief that the human visual system is sensitive to the logarithm
of the EM spectrum and hence most astronomical magnitude
3
Similarly, absolute magnitude, M , is used to represent the
absolute brightness of a star and its relation to the apparent
magnitude is given by the distance modulus equation:
b
= 5 · log10 dp − 5
(12)
B
where dp is the distance in parsecs. Inverting this formula,
the star distance in parsecs can be obtained in terms of the
difference between apparent and absolute magnitudes:
m−M
−2.5 · log10
=
dp
=
10
0.2(m−M +5)
(13)
Now, to relate the magnitude information of a star given in
a star catalog to the amount of photons we observe at the top
of Earth’s atmosphere, we first relate the luminosity of a star
to its absolute magnitude by 1 ,
Fig. 4. The Hertzsprung-Russell diagram shows how the size,
color, luminosity, spectral class, and absolute magnitude of
stars relate. Each dot in the image represents a star whose
absolute magnitude and spectral class have been determined.
The above plots are made using the Hipparcos catalog for which
the effective temperatures for the stars are calculated using their
B-V color indices according to [7].
systems assume a form similar to
m = −2.5 · log10 (f (·)/Q(·))
(8)
where m is the brightness magnitude assigned to a star observed from Earth, f (·) is the mean spectral flux density at
top of Earth’s atmosphere averaged over a defined band and
Q(·) is the normalizing constant for that band [8]. We will not
go into more details about astronomical magnitude systems
but only relate them to the physical brightness values (more
information can be found in [8], [9]). We will consider the
Johnson-V magnitude system for our derivations as it is the
most frequently used one in which the star Vega (Alpha Lyra)
has the magnitude 0 and the magnitudes for other stars are
assigned by comparing their brightnesses to Vega.
The magnitude of a star with respect to Earth is called as
the apparent magnitude and the relation between two magnitude
values is given as:
m1 − m2 = −2.5 log10
b1
b1
⇒
= 10−0.4(m1 −m2 )
b2
b2
(9)
By using Equations 7 and 9, we can derive the following
formula for two stars with equal luminosity values:
m1 − m2 = −5 · log10
d2
.
d1
(10)
From this equation it follows that apparent magnitude favors
closer stars, i.e. assigns a lower value to them. This is not
surprising or unexpected since the apparent magnitude is used
to represent the brightness of the star observed from the Earth.
Stars closer to Earth, even though they may emit less energy,
might seem brighter than more energetic far away ones. In
order to remove this dependence of the brightness measure to
the distance with respect to an observation point, astronomers
compute the absolute brightness of the stars. Absolute brightness, B, is defined as the brightness of a star when observed
from a 10 parsec distance (1 parsec = 3.086 · 1016 meters):
B=
L
4π(10 parsec)2
(11)
L = Lo 10
0.4(Mo −M )
(14)
where (.)o represent the respective quantities for the Sun.
Luminosity is also related to the surface temperature and
surface radius, R, of a star through the Stefan’s Law2 [5] as
L
2π 5 k4
with σ =
(15)
4
σT
15h3 c2
for which σ is known as the Stefan’s constant. Therefore, the
rate, RT (M ), at which a star of absolute magnitude M generates photons at its surface could be computed by combining
Equations 5, 15 and 14:
photon
RT (M ) = Φ(T ) · 4πR2
s
4πR2 =
L
α L
= ·
σ T4
σ T
αLo 10 0.4(Mo −M )
=
·
(16)
σ
T
Finally, by taking into account the distance of a star from the
Earth, we derive the photon irradiance (i.e. number of incident
photons per second per square-meter) over Earth’s atmosphere
in terms of its apparent magnitude and temperature as:
= α T3 ·
Φi (m, T ) =
RT
αLo 10
=
4πd2
400πβ 2 σ
0.4(Mo −m)
T
(17)
where d = β ·10 0.2 (m−M +5) ( β = 3.086·1016 m/pc) is the star
distance in meters (see Eq. 12). Inserting the universal constants
and Sun’s luminosity and absolute magnitude (see Table 1) into
the above equation, photon irradiance equation simplifies to
10−0.4 m
photon
Φi (m, T ) = 7.37 · 1014 ·
(18)
2
m ·s
T
As noted earlier, this is the total photon irradiance, that is, it
covers the whole star emission spectrum. The typical electrooptical systems, however, are only active within a certain
bandwidth and therefore, Equation 6 should be used to weigh
this irradiance with respect to the targeted band.
1. easily derived by combining the equations 7, 9 and 12:
b = bo 10
−0.4 (m−mo )
⇐ from Equation 9
d = do 10
0.2 (m−M −mo +Mo )
⇐ from Equation 12
L = 4πd2 b
=
=
4πd2o bo 10 0.4(Mo −M )
Lo 10 0.4(Mo −M )
2. when applied to a spherical black-body
⇐ from Equation 7
4
As a validation of the formulated model, we compute the
photon irradiance on top of Earth’s atmosphere for a star with
m = 0 and T = 10000K for the wave band of 400-625 nm:
Φi,band = ηT (400, 625) · 7.37 · 10
≈ 0.258 × 7.37 · 1010
≈ 1.90 · 1010
14
10−0.4×0
·
10000
from Figure3-b
photon
m2 ·s
This estimate fits well with the measurement experiment
given in [10] for which the spectral irradiance is reported as
3.64·10−2 W m−2 m−1 for an m = 0 star at 548 nm. The energy
of a photon at 548 nm is 3.63 · 10−19 J and the average photon
count from this energy estimate for the 400-625 nm band is:
3.64 · 10−2
photon
measured
−9
10
Φi
= 225 · 10 ·
≈ 2.25 · 10
m2 ·s
3.63 · 10−19
which is acceptably close to the estimated value considering
the rough approximation of the average photon count above.
One important fact that needs to be noted here is that not
all photons incident on the image sensor are registered by the
electronics. The efficiency of the change of photons to electrons
is called as the Quantum Efficiency (QE) of a sensor and it is
dependent on the wavelength of the light. If the QE of a sensor
could be approximated as uniform across the active band of the
sensor, then the QE value could be taken just as a multiplier
to the computations above. Otherwise, this needs to be taken
into account during the computation of the photon ratio values
by weighing the integrand in Equation 6 to only compute the
number of photons that will be converted to electrons.
3
C AMERA M ODEL
An electro-optical system (EOS) is composed of electrical and
optical components. Electrical system (ES) is made up of the
image sensor that captures the incoming photon flux in terms
of electrical charges and the reader circuitry that digitizes
this charge. Optical systems (OS), on the other hand, are
composed of refractive lenses, reflective mirrors, band filters
and components like teleconverters that guide the incoming
photon flux to the image sensor.
The optical design of the system affects many properties of
the captured image and its quality. For example, the shape and
size of the point spread function (PSF) or its deformations on
the image sensor are two immediate factors that define the
sharpness and resolution of the final image directly. However,
since we are only concerned with the SNR of the signal for this
study, we will not go into advanced optical designs but only
model it as a simple optical system.
A camera system is most importantly defined by three
parameters: field of view (FoV), focal length and image resolution. The FoV is the solid angle through which the camera is
sensitive to electromagnetic radiation. It represents the relation
between the sensor dimensions and the focal length. The
relation between these quantities is given as
0
θ
w̄
w·p
tan
=
=
(19)
2
2f
2f
where θ0 is the field of view in radians, w̄ is the width of the
sensor in meters, w is the width of the sensor in pixels, f is
the focal length in meters and p is the size of a pixel in meters
(see Table 2 for camera related parameters). Note that FoV is
sometimes defined with respect to the diagonal of the image
sensor. Here, we define it with respect to the width alone.
TABLE 2
Parameter Definitions
θ
θ0
δ
f
w̄
w
p
f#
a
A
QE
FF
κlens
L
κband
κoptic
σro
Idark
Ωspot
vslew
βslew
Ωslew
ρ
τ
τd
ε(m)
mback
εback
field of view
field of view
pixel coverage
focal length
sensor width
resolution in horizontal direction
pixel size
f-number
aperture diameter
aperture area
quantum efficiency
fill-factor
lens transmittance
number of lens elements
band filter transmittance
optical transmittance
read-out noise deviation
dark current
spot area
relative slew motion of the object
distance traveled by the spot under
slew motion
area irradiated by the spot under slew
motion
percentage of light falling on the center pixel of the spot
exposure time
dwell time
electrons generated per second for a
star of magnitude m
sky background
sky background electrons generated
per second per pixel
degrees
radians
degrees/pixel
m
m
pixel
m
m
m2
%
%
%
%
%
e−
e− /s
pixel2
degrees/s
pixel
pixel2
%
s
s/pixel
e− /s
mag/(00 )2
e− /s
The amount of light that falls on the sensor is related with
the area of the aperture of the optical system. The aperture is
generally constructed as a circular opening and its diameter is
related to the focal length of the camera through a parameter
named as the f-number:
f# = f /a
(20)
Then, the area for which the light enters the optical system,
called as the aperture area, is equal to:
2
a2
w·p
A=π·
=π·
.
(21)
4
4 tan(θ0 /2) f#
The photon flux entering the camera is focused on an area,
called as the spot area (Ωspot ), on the image plane. Depending
on the optical design, the spot area could cover more than one
pixel and the incoming flux could be shared between several
pixels. At each pixel, photons falling on the photo-sensitive
part of the pixel is converted to electrons. The photo-sensitive
pixel area could cover the full pixel area or it could cover a
fraction of it where some part of the pixel surface is reserved
for electronics. This ratio of the photo-sensitive area to full pixel
area is known as the fill-factor (FF).
Beyond the losses incurred due to the fill-factor and quantum
efficiency, there are some optical factors that reduce the generation of the electrons in the pixels. The lenses are not perfect
5
transmitters of light and so each lens element in the optical
chain reduces the photon flux in some measure. For example,
if an optical system is composed of L lens elements each with
κlens transmittance and a band filter with κband transmittance,
the overall optical lens transmittance is equal to3 :
κoptics = (κlens )2L · κband
(22)
With the defined camera model, we now formulate the
amount of electron flux for a point light source. The number of electrons generated per second for a star with visual
magnitude m and temperature T (assuming a constant QE
profile4 throughout the observed band and no atmospheric
degradation) is:
ε(m, T ) = Φi (m, T ) · ηT (λ0 , λ1 ) · κoptics · QE · F F · A
4
(23)
S OURCES OF N OISE
In the last section, we have detailed how to model the rate
of electrons generated by observing a star. Here, we will talk
about the sources of noise in the capture process.
4.1
Shot Noise
The first source of noise is the light source itself. The intensity
of the light source is related with the amount of photons it
emits per second. This stream or flux of the photons, however,
is not deterministic; it exhibits fluctuations in a Poisson distribution characteristic. This variability is seen as noise in images
and termed as the shot noise or photon noise with a standard
deviation equal to the square root of the average signal itself.
As this noise is directly related with the amount of incoming
photons, it is dependent on the exposure time.
4.2
Read-Out Noise
During reading of the pixel data, electrons collected by the
pixel elements are converted to a voltage proportional to their
number with some amplification and then digitized in an
analog-to-digital converter (ADC) to produce the image raw
data in what is called as analog-to-digital units (ADU) or data
numbers (DN). Ideally, the raw values recorded for the pixels
will directly be proportional to the electron counts in the pixels
but due to fluctuations and noise in the ADC and voltage
amplification units, the raw values also exhibit noise. This noise
is called as the read-out noise; it is independent of the exposure
time and is usually provided by the manufacturers in units of
electrons, i.e. σro = 10 e− .
4.3
Dark Noise
As we have mentioned earlier, an image sensor is a device
that senses the incoming light by counting the number of
electrons excited by it. Thermal conditions, however, also cause
electrons to be generated which are indistinguishable from
the electrons generated by photon absorption. The generation
of electrons due to thermal agitation is termed as the dark
current and it is relatively constant over time at a given
temperature. However, while the constant component of this
noise source could be easily removed from the source signal,
it also exhibits fluctuations following Poisson statistics, which
3. The lens transmittance is doubled for each lens element as they
are normally specified for a single face of the lens.
4. If a variable QE response is included for the computation of ηT ,
then it should not appear again in this formuation.
is called as the dark noise. The dark noise has a standard
deviation equal to the square root of the average number of
electrons generated
√ by the dark current in a given exposure
time, i.e. σdark = Idark × τ .
4.4
Background Noise
In Earth based observations, even if no visible astronomical
sources are within a field of view, there will be some amount
of luminosity present due to light diffusion and atmospheric
scattering. The background luminosity level depends on location, weather conditions, proximity to human settlements and
also it is heavily influenced by the phases of the moon. It is
given in units of apparent magnitude per arcseconds-squared,
i.e. mback = 22/arcsecond2 in the visible band. The number of
electrons generated by the sky background per second for a
pixel is computed as:
εback = εi (mback ) · (δ ∗ 3600)2 with δ =
θ
w
(24)
where δ is the pixel coverage or per-pixel field of view that
represents the amount of solid angle seen by a single pixel and
it is multiplied by 3600 to convert it to arcseconds.
4.5
Other Noise Sources
There are other sources of noise in an image sensor such as the
pixel response non-uniformity or dark-signal non-uniformity
which are caused by the variations in the manufacturing
process, pixel-to-pixel cross-talk or cross-talk asymmetry that
is related with the design of the pixel elements, and rolling
shutter related noise non-uniformity across the sensor. These,
however, are beyond the scope of this study and therefore will
be ignored.
Additionally, for Earth bound observations, one needs to
take into account the atmospheric effects (AE) on the image
quality. Most important of these factors are atmospheric extinction, the absorption and scattering of light due to gas and dust
particles, and astronomical seeing, the blurring and twinkling of
astronomical objects caused by turbulent air masses varying
the optical refractive index throughout the path of the light
ray in the atmosphere and thereby bending the rays in various
amounts during exposure. These effects are most degrading
in hot and low altitude observation sites close to cities and
least degrading at mountain tops which is the reason why
most of the observatories are placed in those remote sites. Even
though AE are very important for the signal quality, they do
not directly influence the camera design parameters considered
in this study. Therefore, they are left beyond the scope and
assumed non-existent.
5
SNR C OMPUTATION
Given the flux estimation model of Section 2, the camera model
given in Section 3 and the noise model of Section 4, we are now
ready to present the formula for the computation of the SNR.
We will provide two different SNR computations: one for the
full spot formed on the image sensor termed as the Spot SNR
and the other one is for the center pixel of the spot termed as
Pixel SNR5 . Additionally, we will also model the SNR formulas
for static and dynamic observation cases. Similar modelings for
the SNR are also presented in [11] and [12].
5. Sometimes also referred to as Peak SNR
6
of generality. The speed is represented as vslew and given in
terms of deg/s. To estimate the size of the area irradiated by
the moving spot on the image sensor, we first compute the
movement in terms of pixels:
βslew =
vslew · τ
.
δ
(28)
The irradiated spot area (see Figure 5 for visualization) can
then be approximated as:
Ωslew =
Fig. 5. Image sensor model. On the left the geometry of a pixel
and the conceptual representation of the fill-factor is shown. On
the right, the image sensor is visualized with fixed and dynamic
conceptualized light spots. The computation of the slew spot
area is related with spot movement and spot’s single dimension.
5.1
Static Formulation
Signal to noise ratio is simply modeled as the ratio of the
number of electrons formed by the incoming photon flux to
the electrons generated due to noise. The per pixel noise is the
electrons gathered in a pixel due to read-out, dark noise and
the sky background (only for earth based observations) in a
given exposure time, τ :
2
σpixel
=
2
σro
+ Idark · τ + εback · τ
(29)
The formula for the dynamic Spot SNR simply uses the
updated spot area size and becomes:
ε·τ
.
SN Rspot = q
2
ε · τ + Ωslew · σpixel
(30)
Pixel SNR computation, however, needs a bit more attention.
Since the light spot is moving on the image plane, an individual
pixel is not irradiated by the source during the full exposure
time but only during when the spot is over the pixel. This
duration is called as the dwell time, τd , and computed as
τd =
δ
θ
=
for τd ≤ τ.
vslew
w · vslew
(31)
(25)
Then, the Spot SNR is found by considering the shot noise of
the signal and per pixel noise over the spot area:
ε·τ
SN Rspot = q
(26)
2
ε · τ + Ωspot · σpixel
Electron generation rate, ε, is found for each star separately
by using its apparent magnitude and temperature according to
Equation 23. We also measure the SNR value for the center of
the spot according to:
ρ·ε·τ
SN Rpixel = q
(27)
2
ρ · ε · τ + σpixel
with ρ being the portion of the light energy incident on the
center pixel. In the static case, spot and pixel SNRs will be
close to each other but the difference will be more important
in the dynamic case. Note that, for optical systems where the
light spot is focused entirely on a single pixel (i.e, Ωspot = 1)
either due to optics or due to using large pixels, the pixel
and spot SNR values will be the same. However, for tasks
requiring accurate localization of star centroids such as star
tracker applications, spots are formed to cover multiple pixels
in order to allow for sub-pixel localization of them using
centroding.
5.2
p
p
Ωspot ·
Ωspot + βslew
Dynamic Formulation
We formulate here how to measure the Spot and Pixel SNRs
for the situations where the camera and the observed stars are
in relative motion with respect to each other. This situation
is often encountered in space based observations where the
satellite is making a slew motion or in Earth based observations where the camera is fixed relative to Earth, not to the
inertial reference frame. We model the motion simply as a
one dimensional horizontal motion of the camera without loss
Then the dynamic Pixel SNR becomes:
ρ · ε · τd
SN Rpixel = q
.
2
ρ · ε · τd + σpixel
(32)
Note that even though source electrons are generated only
during the dwell period, each pixel continues to be exposed by
the sky background and produce dark current for the duration
of the exposure time. Therefore, per pixel noise still has to be
calculated according to Eq. 25 using the full exposure time.
From the dynamic Pixel SNR formulation, it can be seen
that while capturing the image of a fast moving target (i.e.
τd < τ ), increasing the exposure time will reduce the individual
pixel’s SNR value. This insight is not readily apparent from
the Spot SNR formulation as it measures the SNR value for
the joint pixels however the signal might be spread over the
image plane. Therefore, capturing multiple images with short
exposures and then combining the results, instead of capturing
a single image with the exposure time equaling to the sum
of multiple exposures will produce a much better joint SNR
value. To see this, let us assume that we take N individual
short images with exposure time equal to a single pixel’s dwell
time such that τ = N · τd and the irradiated spot area covers
the exact same number of pixels as in the long exposure. The
joint SNR value of the combined images will then be equal to:
2
σpixel
(τd )
=
SN Rjoint
=
2
σro
+ εback · τd + Idark · τd
ε · τd · N
q
2
ε · τd · N + Ωslew · σpixel
(τd )
(33)
(34)
Here, while the nominator is the same as it would be in a
long exposure, the denominator reduces due to the decrease of
dark noise and background sky present in each image because
of the reduced exposure time and, hence, the SNR improves.
7
TABLE 3
Camera Parameters
w
1024
p
18 microns
f#
L
κband
filter band
FoV, θ
exposure, τ
400 - 800 nm
w
2048
15 degrees
p
24 microns
20 ms
6 elements
κlens
98 %
100 %
κatm
100 %
FF
90%
σro
30 e−
Idark
10 e− /s
40%
Ωspot
9 pix2
3 deg/s
mback
-
ρ
vslew
QE
f#
L
κband
50%
FF
2.0
filter band
FoV, θ
exposure, τ
400 - 800 nm
4 degrees
1s
6 elements
κlens
98 %
100 %
κatm
95 %
90%
50%
Idark
10 e− /s
40%
Ωspot
9 pix2
vslew
1/240 deg/s
mback
21 mag/”2
σro
ρ
30
e−
QE
f (Eq 19)
70.002 mm
a (Eq 20)
4.375 cm
f (Eq 19)
703.765 mm
a (Eq 20)
35.188 cm
A (Eq 21)
15.034 cm2
δ (Eq 24)
52.734”
A (Eq 21)
972.489 cm2
δ (Eq 24)
7.031”
τd (Eq 31)
4.883 ms
4.096 pixels
τd (Eq 31)
468.758 ms
βslew (Eq 28)
Ωslew (Eq 29)
15.400 pix2
κoptics (Eq 22)
Ωslew (Eq 29)
6
1.6
TABLE 4
Telescope Parameters
21.288 pix2
βslew (Eq 28)
κoptics (Eq 22)
78.472 %
S IMULATION R ESULTS
In this section, we show some numerical results and plots
for the computed SNR values for a given camera system
and a 35-cm telescope system and demonstrate the effect of
the parameter changes to the signal quality. The camera and
telescope parameters are presented in Table 3 and in Table 4,
respectively.
In Table 5, we show the numerical values for some of
the quantities we have formulated in previous sections for 9
different stars with 3 different temperatures and 3 different
apparent magnitude values for the ease of reproducibility for
future numerical comparison studies. The table shows the flux,
electron generation rate, computed pixel and spot electron
counts and their respective noise levels and the computed SNR
values under dynamic observation conditions for the camera
system given in Table 3.
In Figure 6, a simulation is run for the Table 3 camera for
different {pixel size - f# } combinations for stars with T =
10000K in the magnitude range [5.5, 6.5]. From the figure, it
can be seen that one can achieve similar signal quality levels
for {p = 15 micron f# = 1.4 } and {p = 18 micron f# = 1.6}
setups. However, with the latter setup, the aperture diameter
is also larger (a =4.167 cm vs a =4.375 cm) which might be
undesirable for optical and weight constraints of the system.
In Figure 7, we investigate the effect of the sky background
brightness on the SNR of three T = 10000K stars for the
telescope system given in Table 4. The sky brightness is an
important factor for Earth-bound observation systems and it
exhibits large variations with respect to observation location
and is especially effected by the phases of the Moon. On a
clear night, away from the city lights and when the Moon is
in its new moon phase, sky brightness could reduce to around
m = 22mag/002 . However, during full moon phase, brightness
levels could rise to about m = 17 mag/002 in the U-band [13].
It can be seen in Figure 7 that, the SNR is effected significantly.
Therefore, it is important to factor in the atmospheric conditions and Moon phases for Earth based observations. Note that
we have not taken into account the atmospheric extinction of
the incoming photon flux in this simulation. For more realistic
calculations, a portion of the source flux needs to be degraded
based on observation conditions ( like location, humidity and
time ).
7
2.133 pixels
78.472 %
C ONCLUSION
In this study, we present a Black-body formulation for the
computation of the SNR of astronomical images of stars with
known brightness and temperature values for a given set of
camera parameters. Although the derivation of the incident
stellar photon flux and modeling the SNR in terms of stellar
brightness and camera parameters is a very important requirement before designing an astronomical observation system,
we are unaware of a resource that comprehensively presents
it from an image processing point of view. In this study, by
combining research results from different disciplines such as
physics, astronomy, optics and electronics, we aim to remedy
this situation and present a complete formulation that relates
the full image chain from the source to the finally captured
image for easy reference for other researchers working with
astronomical observation systems.
R EFERENCES
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
[12]
[13]
Robert D. Fiete, Modeling the imaging chain of digital cameras,
Bellingham, Wash. SPIE Press, 2010.
Simon F. Green and Mark H. Jones, An Introduction to Sun and
Stars, Cambridge University Press, 2006.
B. C. Reed, “Stellar magnitudes and photon fluxes,” Journal of the
Royal Astronomical Society of Canada, p. 123, 4 1993.
Max Planck, The Theory of Heat Radiation, Massius M (translator),
P. Blakiston’s Son & Co, 1914.
R. B. Leighton, Principles of Modern Physics, McGraw-Hill, 1959.
Webpage, “ASTM standard extraterrestrial spectrum reference
E-490-00,”
http://rredc.nrel.gov/solar/spectra/am0/ASTM2000.html,
2000.
G. Torres, “On the use of empirical bolometric corrections for
stars,” Astronomical Journal, 2010.
Michael S. Bessell, “Standard photometric systems,” Annual
Reviews of Astronomy and Astrophysics, 2005.
Eugene. F. Milone and Christiaan Sterken, Astronomical Photometry: Past, Present and Future, Springer, 2011.
J.B. Oke and R. E. Schild, “The absolute spectral energy distribution of Alpha Lyrae,” Astrophysical Journal, 1970.
Thomas Schildknecht, Optical astrometry of fast moving objects using
CCD detectors., Institut für Geodsie und Photogrammetrie, 1994.
Herbert Raab, “Detecting and measuring faint point sources with
a ccd.,” in Meeting on Asteroids and Comets in Europe, 2002.
Webpage, “Optical sky background,” http://www.gemini.edu/node/
10781?q=node/11449, 2014.
8
TABLE 5
Numerical Evaluations for the Camera Specified in Table 3
T
Apparent Mag
Flux
Φ(m,T )
ε(m, T )
Spot e− s
Pixel e− s
Spot Noise
Pixel Noise
SN Rspot
SN Rpixel
e− /s
e−
e−
e−
e−
-
-
K
-
photon
m2 ·s
5000
5000
5000
5.50
6.00
6.50
2.17e+08
1.37e+08
8.65e+07
115390
72806
45938
2307.80
1456.13
918.75
225.37
142.20
89.72
146.53
143.60
141.71
33.55
32.29
31.46
15.75
10.14
6.48
6.72
4.40
2.85
8000
8000
8000
5.50
6.00
6.50
2.22e+08
1.40e+08
8.82e+07
117647
74230
46836
2352.95
1484.61
936.72
229.78
144.98
91.48
146.68
143.69
141.78
33.62
32.33
31.49
16.04
10.33
6.61
6.84
4.48
2.90
11000
11000
11000
5.50
6.00
6.50
1.60e+08
1.01e+08
6.37e+07
84928
53586
33810
1698.56
1071.72
676.21
165.88
104.66
66.04
144.44
142.25
140.85
32.65
31.70
31.08
11.76
7.53
4.80
5.08
3.30
2.12
Fig. 6. Pixel and Spot SNR Curves: We plot the estimated SNR curves for the camera system given in Table 3 with respect to
changing star brightness. Left shows the Pixel SNR and right shows the Spot SNR with varying pixel size and f-number parameters
where all other parameters are set according to their values given in the upper half of the table.
Fig. 7. Sky Background Effects on SNR: The background noise experiments are performed for the telescope setup given in
Table 4. Left: SN RSpot vs apparent magnitude for constant background brightness levels. This plot could be used to determine up
to what magnitude stars could be detected for the designed telescope under a given background brightness level. For example if
SN R = 3 is required for detection, only stars up to m = 15 could be seen when the observation is done in a bright background
whereas m = 16 stars could also be observed with the same telescope on a more clear night. Right: Effect of the increasing (going
from right to left of the x-axis) background brightness on the SNR of three stars with apparent magnitudes m = 13, 15 and 17.