Download Quadratic Functions

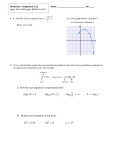
Quadratic Functions; Parabolas
 Graph of a Quadratic Function
The graph of the function
𝒇(𝒙) = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄
is a parabola that opens upward (concave up), and the vertex is minimum, if 𝒂 > 𝟎. The parabola opens
downward (concave down), and the vertex is a maximum, if 𝒂 < 𝟎.
The larger the value of |𝒂|, the more narrow the parabola will be.
−𝒃
−𝒃
Its vertex is at the point ( 𝟐𝒂 , 𝒇 ( 𝟐𝒂 )).
The axis of symmetry of the parabola has equation 𝒙 =
𝟐
−𝒃
𝟐𝒂
𝟐𝒂
𝒇(𝒙) = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 𝒘𝒊𝒕𝒉 𝒂 > 𝟎
𝒇(𝒙) = 𝒂𝒙 + 𝒃𝒙 + 𝒄 𝒘𝒊𝒕𝒉 𝒂 < 𝟎
Vertex: (
−𝒃
Axis of
−𝒃
, 𝒇 ( ))
𝟐𝒂
Symmetry
𝒙=
−𝒃
𝟐𝒂
x
x
Axis of
Symmetry
𝒙=
−𝒃
Vertex: (
−𝒃
𝟐𝒂
𝟐𝒂
−𝒃
, 𝒇 ( ))
Y
Y
EX) (a) Determine if the function is quadratic. If it is, (b) determine if the graph is concave up or concave down. (c) Determine if the
vertex of the graph is a maximum point or a minimum point.
1. 𝑓(𝑥) = 𝑥 2 + 4𝑥 + 4
𝒂 = 𝟏 𝒂𝒏𝒅 𝒃 = 𝟒. Since 𝒂 > 𝟎, The graph is concave up with the minimum vertex.
−𝒃
Vertex: (
x-coordinate of the vertex is
−𝒃
𝟐𝒂
=
−𝟒
𝟐(𝟏)
𝟐𝒂
−𝒃
, 𝒇 ( )) = (−𝟐, 𝟎)
𝟐𝒂
= −𝟐
−𝒃
y-coordinate of the vertex is 𝒇 ( ) = 𝒇(−𝟐) = (−𝟐)𝟐 + 𝟒(−𝟐) + 𝟒 = 𝟒 − 𝟖 + 𝟒 = 𝟎
𝟐𝒂
2. 𝑔(𝑥) = −2𝑥 2 − 4𝑥 + 6
𝒂 = −𝟐 𝒂𝒏𝒅 𝒃 = −𝟒. Since 𝒂 < 𝟎, The graph is concave down with the maximum vertex.
−𝒃
Vertex: (
x-coordinate of the vertex is
−𝒃
𝟐𝒂
=
−𝒃
−(−𝟒)
𝟐(−𝟐)
=
𝟒
−𝟒
𝟐𝒂
−𝒃
, 𝒇 ( )) = (−𝟏, 𝟖)
𝟐𝒂
= −𝟏
y-coordinate of the vertex is 𝒇 ( ) = 𝒇(−𝟏) = −𝟐(−𝟏)𝟐 − 𝟒(−𝟏) + 𝟔 = −𝟐 + 𝟒 + 𝟔 = 𝟖
𝟐𝒂
𝟐𝒂
EX) Suppose the monthly revenue from the sale of Carlson 42-inch plasma televisions is given by the function
𝑅(𝑥) = −0.1𝑥 2 + 600𝑥 𝑑𝑜𝑙𝑙𝑎𝑟𝑠
where x is the number of televisions sold.
a. Find the vertex and the axis of symmetry of the graph of this function.
The function is a quadratic function with 𝒂 = −𝟎. 𝟏, 𝒃 = 𝟔𝟎𝟎. The x-coordinate of the vertex is
−𝒃
𝟐𝒂
=
−𝟔𝟎𝟎
𝟐(−𝟎.𝟏)
= 𝟑𝟎𝟎𝟎, and the axis of symmetry is the line 𝒙 = 𝟑𝟎𝟎𝟎. The y-coordinate of the vertex is
𝑹(𝟑𝟎𝟎𝟎) = −𝟎. 𝟏(𝟑𝟎𝟎𝟎)𝟐 + 𝟔𝟎𝟎(𝟑𝟎𝟎𝟎) = 𝟗𝟎𝟎, 𝟎𝟎𝟎
So the vertex is (3000,900,000).
b. Determine if the vertex represents a maximum or minimum point.
Vertex: (3000, 900,000)
Because 𝒂 < 𝟎, the parabola opens downward (concave down),
so the vertex is a maximum point.
c. Interpreted the vertex in the context of the application.
The x-coordinate of the vertex gives the number of televisions that
must be sold to maximize revenue, so selling 3000 sets will result
in the maximum revenue. The y-coordinate of the vertex gives
the maximum revenue, $900,000.
Axis of symmetry
 Vertex Form of a Quadratic Function
In general, the graph of the function
𝒚 = 𝒂(𝒙 − 𝒉)𝟐 + 𝒌
is a parabola with its vertex at the point (𝒉, 𝒌).
The parabola opens upward if 𝒂 > 𝟎, and the vertex is a minimum.
The parabola opens downward if 𝒂 < 𝟎, and the vertex is maximum.
The axis of symmetry of the parabola has equation 𝒙 = 𝒉.
The a is the same as the leading coefficient in 𝑦 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐, so the larger the value of |𝒂|, the
more narrow the parabola will be.
EX) (a) Is the vertex a maximum or minimum? (b) Give the coordinates of the vertex
1.𝑓(𝑥) = 2(𝑥 − 4)2 − 6
𝒂 = 𝟐 𝒂𝒏𝒅 𝒂 > 𝟎, the vertex is a minimum.
Vertex: (𝟒, −𝟔)
2. 𝑔(𝑥) = −0.5(𝑥 + 2)2 + 1
𝒂 = −𝟎. 𝟓 𝒂𝒏𝒅 𝒂 < 𝟎 , the vertex is a maximum.
Vertex: (−𝟐, 𝟏)
Solving Quadratic Equations
 Zero Product Property
For real numbers a and b, the product 𝒂𝒃 = 𝟎 if and only if either 𝒂 = 𝟎 or 𝒃 = 𝟎 or both a and b are zero
EX) Solve the equation 3𝑥 2 + 7𝑥 = 6
We firs subtract 6 from both sides of the equation to rewrite the equation with 0 on one side:
𝟑𝒙𝟐 + 𝟕𝒙 − 𝟔 = 𝟎
To begin factoring the trinomial 𝟑𝒙𝟐 + 𝟕𝒙 − 𝟔, we seek factors of 𝟑𝒙𝟐 (that is, 3x and x) as the first terms of two binomials and
factors of -6 as the last terms of the binomial. The factorization whose inner and outer products combine to 7x is (𝟑𝒙 − 𝟐)(𝒙 +
𝟑), so we have
(𝟑𝒙 − 𝟐)(𝒙 + 𝟑) = 𝟎
Using the zero product property gives
𝟑𝒙 − 𝟐 = 𝟎 𝒐𝒓 𝒙 + 𝟑 = 𝟎
Solving these linear equations gives the two solutions to the original equation.
𝒙=
𝟐
𝒐𝒓 𝒙 = −𝟑
𝟑
 Quadratic Formula
The solutions of the quadratic equation 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 = 0 are given by the formula
𝒙=
−𝒃 ± √𝒃𝟐 − 𝟒𝒂𝒄
𝟐𝒂
Note that a is the coefficient of 𝑥 2 , b is the coefficient of x, and c is the constant term.
 The Discriminant
We can also determine the type of solutions a quadratic equation has by looking at the expression 𝒃𝟐 −
𝟒𝒂𝒄, which is called the discriminant of the quadratic equation 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 = 0. The discriminant is
the expression inside in the quadratic formula 𝑥 =
−𝑏±√𝑏 2 −4𝑎𝑐
2𝑎
, so it determines if the quantity inside the
radical is positive, zero, or negative. Thus, we have



𝒃𝟐 − 𝟒𝒂𝒄 > 𝟎, there are two different real solutions.
𝒃𝟐 − 𝟒𝒂𝒄 = 𝟎, there are one real solution.
𝒃𝟐 − 𝟒𝒂𝒄 < 𝟎, there are no real solution.
 Connections Between Graphs of Quadratic Functions and Solution Methods
y
y
y
Graph
x
a
b
x
x
Type of x-Intercepts
Graph crosses x-axis twice.
Graph touches but does not
cross x-axis.
Graph does not cross the xaxis.
Type of Solutions
Equation has two real
solutions.
Equation has one real solution.
Equation has not real solutions.
Suggested Solution Methods
Use factoring, graphing, or
quadratic formula.
Use factoring, graphing, or the
square root method.
Use quadratic formula to verify
that solutions are not real.
EX) Solve the equations:
a. 𝑥 2 − 3𝑥 + 5 = 0
Using the quadratic formula, with 𝒂 = 𝟏, 𝒃 = 𝟑, 𝒂𝒏𝒅 𝒄 = 𝟓, gives
𝒙=
−(−𝟑) ± (−𝟑)𝟐 − 𝟒(𝟏)(𝟓) 𝟑 ± √−𝟏𝟏 𝟑 ± 𝒊√𝟏𝟏
=
=
𝟐(𝟏)
𝟐
𝟐
Since 𝒃𝟐 − 𝟒𝒂𝒄 < 𝟎, there are no real solution and the solutions are the complex numbers.
b. 3𝑥 2 + 4𝑥 = 3
Writing 3𝑥 2 + 4𝑥 = −3 in the form 3𝑥 2 + 4𝑥 − 3 = 0 gives 𝒂 = 𝟑, 𝒃 = 𝟒, 𝒂𝒏𝒅 𝒄 = −𝟑, so the solutions are
𝒙=
−𝟒 ± 𝟒𝟐 − 𝟒(𝟑)(−𝟑) −𝟒 ± √𝟏𝟔 + 𝟑𝟔 −𝟒 ± √𝟓𝟐 −𝟒 ± 𝟐√𝟏𝟑 −𝟐 ± √𝟏𝟑
=
=
=
=
𝟐(𝟑)
𝟔
𝟔
𝟔
𝟑
Since 𝒃𝟐 − 𝟒𝒂𝒄 > 𝟎, there are two real solutions, which is
−𝟐+√𝟏𝟑
𝟑
and
−𝟐−√𝟏𝟑
𝟑
.
Piecewise-Defined Functions
 Piecewise-Defined Functions
It is possible that a set of data cannot be modeled with a single equation. We can use a piecewise-defined
function when there is not a single function that accurately represents the situation. A piecewise-defined
function is so named because it is defined with different pieces for different parts of its domain rather
than one equation.
EX) Excluding fuel adjustment costs and taxes, Georgia Power Company charges its residential power customers for electricity during
the months of June through September according to Table.
Monthly Kilowatt-hours (kWh)
Monthly Charge
0 to 650
More than 650, up to 1000
More than 1000
$7.50 plus $0.04657 per kWh
$37.77 plus $0.07738 per kWh above 650
$64.85 plus $0.07976 per kWh above 1000
a. Write the piecewise-defined function C that gives the monthly charge for residential electricity, with input x equal to the monthly
number of kilowatt-hours
𝟕. 𝟓𝟎 + 𝟎. 𝟎𝟒𝟔𝟓𝟕𝒙
𝟑𝟕. 𝟕𝟕 + 𝟎. 𝟎𝟕𝟕𝟑𝟖(𝒙 − 𝟔𝟓𝟎)
𝟔𝟒. 𝟖𝟓 + 𝟎. 𝟎𝟕𝟗𝟕𝟔(𝒙 − 𝟏𝟎𝟎𝟎)
𝑪(𝒙) =
𝒊𝒇 𝟎 ≤ 𝒙 ≤ 𝟔𝟓𝟎
𝒊𝒇 𝟔𝟓𝟎 < 𝒙 ≤ 𝟏𝟎𝟎𝟎
𝒊𝒇 𝒙 > 𝟏𝟎𝟎𝟎
where C(x) is the charge in dollars for x kWh of electricity.
b. Find C(950) and explain what it means.
To evaluate C(950), we must determine which “piece” defines the function when 𝒙 = 𝟗𝟓𝟎. Because 950 is between 650 and 1000,
we use the “middle piece” of the function:
𝑪(𝟗𝟓𝟎) = 𝟑𝟕. 𝟕𝟕 + 𝟎. 𝟎𝟕𝟕𝟑𝟖(𝟗𝟓𝟎 − 𝟔𝟓𝟎) = 𝟔𝟎. 𝟗𝟖𝟒
Companies regularly round charges up to the next cent if any part of a cent is due. This means that if 950 kWh are used in a
month, the bill is $60.99.
c. Find the charge for using 1560kWh in a month.
To find the charge of 1560 kWh, we evaluate C(1560), using the “bottom piece” of the function because 1560>1000. Evaluating
this gives
𝑪(𝟏𝟓𝟔𝟎) = 𝟔𝟒. 𝟖𝟓 + 𝟎. 𝟎𝟕𝟗𝟕𝟔(𝟏𝟓𝟔𝟎 − 𝟏𝟎𝟎𝟎) = 𝟏𝟎𝟗. 𝟓𝟏𝟓𝟔
so the charge for the month is $109.52.
Transformations of Graphs and Symmetry
 Graph Transformations
 Vertical Shifts of Graphs
If k is a positive real number:
The graph of 𝒈(𝒙) = 𝒇(𝒙) + 𝒌 can be obtained by shifting the graph of 𝒇(𝒙) upward k units.
The graph of 𝒈(𝒙) = 𝒇(𝒙) − 𝒌 can be obtained by shifting the graph of 𝒇(𝒙) downward k units.
 Horizontal Shifts of Graphs
If h is a positive real number:
The graph of 𝑔(𝑥) = 𝑓(𝑥 − ℎ) can be obtained by shifting the graph of 𝒇(𝒙) to the right h units.
The graph of 𝑔(𝑥) = 𝑓(𝑥 + ℎ) can be obtained by shifting the graph of 𝒇(𝒙) to the left h units.
 Stretching and Compressing Graphs
The graph of 𝑦 = 𝑎𝑓(𝑥) is obtained by vertically stretching the graph of 𝑓(𝑥) by a factor of |𝑎| if
|𝑎| > 1, and vertically compressing the graph of 𝑓(𝑥) by a factor of |𝑎| if 0 < |𝑎| < 1.
 Reflections of Graphs Across the Coordinate Axes
1. The graph of 𝑦 = −𝑓(𝑥) can be obtained by reflecting the graph of 𝑦 = 𝑓(𝑥) across the x-axis.
2. The graph of 𝑦 = 𝑓(−𝑥) can be obtained by reflecting the graph of 𝑦 = 𝑓(𝑥) across the y-axis.
3
EX) Suppose the graph of 𝑦 = 𝑥 2 is shifted to the left 4 units. What is the equation that gives the new graph?
3
𝑦 = (𝑥 + 4)2
3
EX) Suppose the graph of 𝑦 = 𝑥 2 is shifted down 5 units and to the right 4 units. What is the equation that gives the new graph?
3
𝑦 = (𝑥 − 4)2 − 5
3
EX) Suppose the graph of 𝑦 = 𝑥 2 is stretched by a factor of 3 and then shifted up 5 units. What is the equation that gives the new graph?
3
𝑦 = 3𝑥 2 + 5
3
1
EX) Suppose the graph of 𝑦 = 𝑥 2 is compressed by the factor of and then shifted right 6 unites. What is the equation that gives the new
5
graph?
3
1
𝑦 = (𝑥 − 6)2
5
 Symmetry with Respect to the y-axis
The graph of 𝑦 = 𝑓(𝑥) is symmetric with respect to the y-axis if, for every point (x, y) on the graph, the
point (-x, y) is also on the graph. That is,
𝒇(−𝒙) = 𝒇(𝒙)
for all x in the domain of f. such a function is called an even function.
 Symmetry with Respect to the Origin
The graph of 𝑦 = 𝑓(𝑥)is symmetric with respect to the origin if, for every point (x, y) on the graph, the
point (-x, -y) is also on the graph. That is,
𝒇(−𝒙) = −𝒇(𝒙)
for all x in the domain of f. such a function is called an odd function.
 Symmetry with Respect to the x-axis
The graph of an equation is symmetric with respect to the x-axis if, for every point (x, y) on the graph,
the point (x, -y) is also on the graph.
EX) determine algebraically whether the graph of each equation is symmetric with respect to the x-axis, y-axis, or origin. Confirm your
conclusion graphically.
a. 𝑦 =
2𝑥 2
𝑥 2 +1
To test for symmetry with respect to the x-axis, we replace y with –y. Because the result,
−𝒚 =
𝟐𝒙𝟐
𝒙𝟐 + 𝟏
is not equivalent to the original function, the graph is not symmetric with respect to the x-axis.
To test for y-axis symmetry, we replace x with –x:
𝒚=
𝟐(−𝒙)𝟐
𝟐𝒙𝟐
=
(−𝒙)𝟐 + 𝟏 𝒙𝟐 + 𝟏
which is equivalent to the original equation. Thus, the graph is symmetric to the y-axis.
To test for symmetry with respect to the origin, we replace x with –x and y with –y:
−𝒚 =
𝟐(−𝒙)𝟐
𝟐𝒙𝟐
=
(−𝒙)𝟐 + 𝟏 𝒙𝟐 + 𝟏
which is not equivalent to the original equation. Thus, the graph is not symmetric with respect to the origin.
(continued…)
(continued…)
b. 𝑦 = 𝑥 3 − 3𝑥
To test for symmetry with respect to the x-axis, we replace y with –y. Because the result
−𝒚 = 𝒙𝟑 − 𝟑𝒙
is not equivalent to the original function, the graph is not symmetric with respect to the x-axis.
To test for y-axis symmetry, we replace x with –x:
𝒚 = (−𝒙𝟑 ) − 𝟑(−𝒙) = −𝒙𝟑 + 𝟑𝒙
which is not equivalent to the original equation. Thus, the graph is not symmetric to the y-axis.
To test for symmetry with respect to the origin, we replace x with –x and y with –y:
−𝒚 = −𝒙𝟑 − 𝟑(−𝒙) = −𝒙𝟑 + 𝟑𝒙, 𝐨𝐫 𝒚 = 𝒙𝟑 − 𝟑𝒙
which is equivalent to the original equation. Thus, the graph is symmetric with respect to the origin.
c. 𝑥 2 + 𝑦 2 = 16
To test for symmetry with respect to the x-axis, we replace y with –y. Because the result
𝒙𝟐 + −𝒚𝟐 = 𝟏𝟔 𝐨𝐫 𝒙𝟐 + 𝒚𝟐 = 𝟏𝟔
This is equivalent to the original equation, so the graph is symmetric with respect to the x-axis.
To test for y-axis symmetry, we replace x with –x:
(−𝒙𝟐 ) + 𝒚𝟐 = 𝟏𝟔 𝐨𝐫 𝒙𝟐 + 𝒚𝟐 = 𝟏𝟔
This is equivalent to the original equation, so the graph is symmetric to the y-axis.
To test for symmetry with respect to the origin, we replace x with –x and y with –y:
(−𝒙𝟐 ) + (−𝒚𝟐 ) = 𝟏𝟔 𝐨𝐫 𝒙𝟐 + 𝒚𝟐 = 𝟏𝟔
which is equivalent to the original equation. Thus, the graph is symmetric with respect to the origin.
Combining Functions; Composite Functions
 Operations with Functions
Operation
Formula
Example with
𝒇(𝒙) = √𝒙 𝐚𝐧𝐝 𝒈(𝒙) = 𝒙𝟑
Sum
(𝑓 + 𝑔)(𝑥) = 𝑓(𝑥) + 𝑔(𝑥)
(𝑓 + 𝑔)(𝑥) = √𝑥 + 𝑥 3
Difference
(𝑓 − 𝑔)(𝑥) = 𝑓(𝑥) − 𝑔(𝑥)
(𝑓 − 𝑔)(𝑥) = √𝑥 − 𝑥 3
Product
(𝑓 ∗ 𝑔)(𝑥) = 𝑓(𝑥) ∗ 𝑔(𝑥)
(𝑓 ∗ 𝑔)(𝑥) = √𝑥 ∗ 𝑥 3
Quotient
(𝑔) (𝑥) = 𝑔(𝑥) (𝑔(𝑥) ≠ 0)
𝑓
𝑓(𝑥)
𝑓
(𝑔) (𝑥) =
√𝑥
𝑥3
(𝑥 ≠ 0)
 Composite Function
The composite function, f of g, is denoted by
(𝒇 ∘ 𝒈)(𝒙) = 𝒇(𝒈(𝒙))
The domain of 𝑓 ∘ 𝑔 is the subset of the domain of g for which 𝑓 ∘ 𝑔 is defined.
The composite function 𝑔 ∘ 𝑓 is defined by
(𝒈 ∘ 𝒇)(𝒙) = 𝒈(𝒇(𝒙))
The domain of 𝑔 ∘ 𝑓 is the subset of the domain of f for which 𝑔 ∘ 𝑓 is defined.
𝑓
EX) Find the following: (a) (𝑓 + 𝑔)(𝑥), (b) (𝑓 − 𝑔)(𝑥), (c) (𝑓 ∗ 𝑔)(𝑥), (d) ( ) (𝑥), (e) (𝑓 ∘ 𝑔)(𝑥), (f) (𝑔 ∘ 𝑓)(𝑥).
𝑔
𝒇(𝒙) = 𝟑𝒙 − 𝟓; 𝒈(𝒙) = 𝟒 − 𝒙
(a) (𝒇 + 𝒈)(𝒙) = 𝟑𝒙 − 𝟓 + 𝟒 − 𝒙
= 𝟐𝒙 − 𝟏
(b) (𝒇 − 𝒈)(𝒙) = 𝟑𝒙 − 𝟓 − (𝟒 − 𝒙)
= 𝟑𝒙 − 𝟓 − 𝟒 + 𝒙
= 𝟒𝒙 − 𝟗
(c) (𝒇 ∗ 𝒈)(𝒙) = (𝟑𝒙 − 𝟓) ∗ (𝟒 − 𝒙)
= (𝟑𝒙)(𝟒) + (𝟑𝒙)(−𝒙) + (−𝟓)(𝟒) + (−𝟓)(−𝒙)
= 𝟏𝟐𝒙 − 𝟑𝒙𝟐 − 𝟐𝟎 + 𝟓𝒙
=
−𝟑𝒙𝟐
+ 𝟏𝟕𝒙 − 𝟐𝟎
𝒇
) (𝒙)
𝒈
(d) (
=
𝟑𝒙−𝟓
𝟒−𝒙
(e) (𝒇 ∘ 𝒈)(𝒙) = 𝒇 𝒈(𝒙)
= 𝟑(𝟒 − 𝒙) − 𝟓
= 𝟏𝟐 − 𝟑𝒙 − 𝟓
= −𝟑𝒙 + 𝟕
(f) (𝒈 ∘ 𝒇)(𝒙) = 𝒈 𝒇(𝒙)
= 𝟒 − (𝟑𝒙 − 𝟓)
= 𝟒 − 𝟑𝒙 + 𝟓
= −𝟑𝒙 + 𝟗
Inverse Functions
 Inverse Functions
Functions f and g for which 𝒈 𝒇(𝒙) = 𝒙 for all x in the domain of g, and 𝒇 𝒈(𝒙) = 𝒙 for all x in the
domain of f, are called inverse functions. In this case, we denote g by 𝒇−𝟏, read as “f inverse.”
The functions f and g are inverse functions if, whenever the pair (a, b) satisfies 𝑦 = 𝑓(𝑥), the pair (b, a)
satisfies 𝑦 = 𝑔(𝑥). Note that when this happens,
𝒇 𝒈(𝒙) = 𝒙 and 𝒈 𝒇(𝒙) = 𝒙
for all x in the domain of g and f, respectively.
EX) The function that can be used to convert a temperature of 𝑥° Celsius to a Fahrenheit temperature is
9
𝐹(𝑥) = 𝑥 + 32
5
The function that can be used to convert a temperature of 𝑥° Fahrenheit back to a Celsius temperature is
𝐶(𝑥) =
5𝑥 − 160
9
To see how the two conversion formulas for temperature are related, find 𝐶(𝐹(𝑥)) and 𝐹(𝐶(𝑥)) and determine if the functions are
inverse functions.
We compute 𝑪(𝑭(𝒙)) and 𝑭(𝑪(𝒙)). Evaluating C at 𝑭(𝒙) gives
𝟗
𝟓 ( 𝒙 + 𝟑𝟐) − 𝟏𝟔𝟎 𝟗𝒙 + 𝟏𝟔𝟎 − 𝟏𝟔𝟎 𝟗𝒙
𝟓
𝑪(𝑭(𝒙)) =
=
=
=𝒙
𝟗
𝟗
𝟗
and evaluating F at 𝑪(𝒙) gives
𝑭(𝑪(𝒙)) =
𝟗 𝟓𝒙 − 𝟏𝟔𝟎
𝟒𝟓𝒙 𝟏𝟒𝟒𝟎
∗(
) + 𝟑𝟐 =
−
+ 𝟑𝟐 = 𝒙 − 𝟑𝟐 + 𝟑𝟐 = 𝒙
𝟓
𝟗
𝟒𝟓
𝟒𝟓
Because 𝑪(𝑭(𝒙)) = 𝒙 and 𝑭(𝑪(𝒙)) = 𝒙, the two functions F and C are inverse.
 Finding the Inverse of a Function
To find the inverse of the function f that is defined by the equation 𝑦 = 𝑓(𝑥):
1. Rewrite the equation replacing 𝒇(𝒙) with y.
2. Interchange x and y in the equation defining the function.
3. Solve the new equation for y. if this equation cannot be solve uniquely for y, the original
function has no inverse function.
4. Replace y with 𝒇−𝟏 (𝒙).
 Graphs of Inverse Functions
The graphs of a function and its inverse are symmetric with respect to the line 𝒚 = 𝒙.
EX) (a) Find the inverse function of 𝑓(𝑥) =
2𝑥−1
3
Using the steps for finding the inverse of a function, we have
𝒚=
𝟐𝒙−𝟏
𝒙=
𝟐𝒚−𝟏
1. Replace 𝒇(𝒙) with y.
𝟑
2. Interchange x and y.
𝟑
𝟑𝒙 = 𝟐𝒚 − 𝟏
3. Solve for y.
𝟑𝒙 + 𝟏 = 𝟐𝒚
𝟑𝒙+𝟏
𝟐
=𝒚
𝒇−𝟏 (𝒙) =
(b) Graph 𝑓(𝑥) =
2𝑥−1
3
𝟑𝒙+𝟏
𝟐
and its inverse function on the same axes.
4. Replace y with 𝒇−𝟏 (𝒙)
𝒇−𝟏 (𝒙) =
𝟑𝒙+𝟏
𝟐
𝒚=𝒙
𝒇(𝒙) =
𝟐𝒙−𝟏
𝟑
Exponential Functions
 Exponential Function
If b is a positive real number, 𝑏 ≠ 1, then the function 𝒇(𝒙) = 𝒃𝒙 is an exponential function. The
constant b is called the base if the function and the variable x is the exponent.
 Exponential Growth Function
Equation:
𝑓(𝑥)
𝒚 = 𝒂 𝒃𝒌𝒙 , 𝒃 > 𝟏, 𝒂 > 𝟎, 𝒌 > 𝟎
*x-intercept:
none
*y-intercept:
(0, a)
*Domain:
all real numbers
*Range:
all real numbers y > 0
*Horizontal asymptote:
x-axis (the line y = 0)
*Shape:
increasing on domain and concave up
x
 Exponential Decay Function
Equation:
𝒚 = 𝒂 𝒃−𝒌𝒙 , 𝒃 > 𝟏, 𝒂 > 𝟎, 𝒌 > 𝟎
𝑓(𝑥)
or
𝒚 = 𝒂(𝒄𝒙 ),
𝟎 < 𝒄 < 𝟏, 𝒂 > 𝟎
*x-intercept:
none
*y-intercept:
(0, a)
*Domain:
all real numbers
x
*Range:
y>0
*Horizontal asymptote:
x-axis (the line y = 0)
*Shape:
decreasing on domain and concave up
EX) determine if the following function is a growth exponential or a decay exponential.
𝑦 = 3−𝑥
𝟏 𝒙
We can write the function 𝒚 = 𝟑−𝒙 in the form 𝒚 = ( ) because
𝟑
𝟑−𝒙 = 𝟑−𝟏
𝒙
𝟏 𝒙
=( )
𝟑
𝟏
In general, a function of the form 𝒇(𝒙) = 𝒛(𝒃−𝒙 ) with b > 1 can also be written in the form 𝒇(𝒙) = 𝒛(𝒄𝒙 ) 0 < c < 1 and 𝒄 = .
𝒃
Functions with equations of this form can be used to model exponential decay.
 Growth and Decay
For initial amount 𝑎 > 0, the equation 𝒚 = 𝒂𝒃𝒌𝒙 for 𝑏 > 1 defines a growth function if 𝑘 > 0 and a
decay function if 𝑑 < 0.
 Transformations of Graphs of Exponential Functions
Graphs of exponential function, like other types of functions, can be shifted, reflected, or stretched.
Transformations, which were introduced in Chapter 4.1, can be applied to graphs of exponential
functions.
Ex) a. Explain how the graph of 𝑦 = 3 𝑥−4 compares to the graph of 𝑦 = 3 𝑥
The graph of 𝒚 = 𝟑𝒙−𝟒 has the same shape as 𝒚 = 𝟑𝒙 , but it is shifted 4 units to the right.
b. Explain how the graph of 𝑦 = 3 𝑥 − 4 compares to the graph of 𝑦 = 3 𝑥
The graph of 𝒚 = 𝟑𝒙 − 𝟒 has the same shape as 𝒚 = 𝟑𝒙 , but it is shifted 4 units down.
c. Explain how the graph of 𝑦 = 2 + 3 𝑥−4 compares to the graph of 𝑦 = 3 𝑥
The graph of 𝒚 = 𝟐 + 𝟑𝒙−𝟒 has the same shape as 𝒚 = 𝟑𝒙 , but it is shifted 4 unis to the right and 2 units up.
d. Explain how the graph of 𝑦 = 5(3𝑥 ) compares to the graph of 𝑦 = 3 𝑥
As we saw in Chapter 4.1, multiplication of functions by a constant greater than 1 stretches the graph of the function
by a factor equal to that constant. Each of the y-values of 𝒚 = 𝟓(𝟑𝒙 ) is 5 times the corresponding y-value of 𝒚 = 𝟑𝒙 .
Logarithmic Functions; Properties of Logarithms
 Logarithmic Function
For x > 0, b > 0, and 𝑏 ≠ 1, the logarithmic function to the base b is
𝒚 = 𝒍𝒐𝒈𝒃 𝒙
which is defined by 𝒙 = 𝒃𝒚
That is, 𝒍𝒐𝒈𝒃 𝒙 is the exponent to which we must raise the base b to get the number x.
This function is the inverse function of the exponential function 𝒚 = 𝒃𝒙 .
EX) 1. Write the logarithmic equations in exponential form; 2𝑦 = 𝑙𝑜𝑔5 𝑥
To rewrite 𝟐𝒚 = 𝒍𝒐𝒈𝟓 𝒙 in exponential form, note that the base of the logarithm, 5, becomes the base of the exponential
expression, and 2y equals the exponent in the equivalent exponential form. That is, the exponential form is
𝟓𝟐𝒚 = 𝒙
2. Write the exponential equations in logarithmic form; 92𝑥 = 𝑦
To rewrite 𝟗𝟐𝒙 = 𝒚 in logarithmic form, note that the base of the logarithm will be 9, the same as the base of the
exponential expression. Also not that 2x is the exponent in 𝟗𝟐𝒙 = 𝒚, so y is the value of the logarithm. That is, the
exponential form of 𝟗𝟐𝒙 = 𝒚 is
𝟐𝒙 = 𝒍𝒐𝒈𝟗 𝒚.
 Natural Logarithms
The logarithmic function with base e is 𝒚 = 𝒍𝒐𝒈𝒃 𝒙, defined by 𝒙 = 𝒆𝒚 for all positive numbers x and
denoted by
𝒍𝒏𝒙 = 𝒍𝒐𝒈𝒆 𝒙
 Basic Properties of Logarithms
For 𝑏 > 0, 𝑏 ≠ 1,
1. 𝒍𝒐𝒈𝒃 𝒃 = 𝟏
2. 𝒍𝒐𝒈𝒃 𝟏 = 𝟎
3. 𝒍𝒐𝒈𝒃 𝒃𝒙 = 𝒙
4. 𝒃𝒍𝒐𝒈𝒃𝒙 = 𝒙
5. For positive real number M and N, if M = N, then 𝒍𝒐𝒈𝒃 𝑴 = 𝒍𝒐𝒈𝒃 𝑵
 Additional Logarithmic Properties
For 𝑏 > 0, 𝑏 ≠ 1, k a real number, and M and N positive real numbers,
Product Property
6. 𝒍𝒐𝒈𝒃 (𝑴𝑵) = 𝒍𝒐𝒈𝒃 𝑴 + 𝒍𝒐𝒈𝒃 𝑵
Quotient Property
7. 𝒍𝒐𝒈𝒃 ( 𝑵 ) = 𝒍𝒐𝒈𝒃 𝑴 − 𝒍𝒐𝒈𝒃 𝑵
Power Property
8.𝒍𝒐𝒈𝒃 𝑴𝒌 = 𝒌 𝒍𝒐𝒈𝒃 𝑴
𝑴
EX) Rewrite the following expressions as a single logarithm.
a. 𝑙𝑜𝑔3 𝑥 + 4 𝑙𝑜𝑔3 𝑦
= 𝒍𝒐𝒈𝟑 𝒙 + 𝒍𝒐𝒈𝟑 𝒚𝟒
Use Logarithmic Property 8.
= 𝒍𝒐𝒈𝟑 𝒙𝒚𝟒
Use Logarithmic Property 6.
1
b. log 𝑎 + 3 log 𝑏
2
= 𝐥𝐨𝐠 𝒂𝟏/𝟐 − 𝐥𝐨𝐠 𝒃𝟑
= 𝐥𝐨𝐠(
𝒂𝟏/𝟐
𝒃𝟑
Use Logarithmic Property 8.
)
Use Logarithmic Property 7.
c. ln(5𝑥) − 3 ln(𝑧)
= 𝐥𝐧(𝟓𝒙) − 𝒍𝒏(𝒛𝟑 )
Use Logarithmic Property 8.
𝟓𝒙
= 𝐥𝐧( 𝟑 )
Use Logarithmic Property 7.
𝒛
EX) a. Use logarithmic properties to estimate ln(5𝑒) if ln 5 ≈ 1.61.
𝐥𝐧(𝟓𝒆) = 𝐥𝐧 𝟓 + 𝐥𝐧 𝒆 ≈ 𝟏. 𝟔𝟏 + 𝟏 = 𝟐. 𝟔𝟏
15
b. Find 𝑙𝑜𝑔𝑎 ( ) if 𝑙𝑜𝑔𝑎 15 = 2.71 and 𝑙𝑜𝑔𝑎 8 = 2.079
8
𝟏𝟓
𝒍𝒐𝒈𝒂 ( ) = 𝒍𝒐𝒈𝒂 𝟏𝟓 − 𝒍𝒐𝒈𝒂 𝟖 = 𝟐. 𝟕𝟏 − 𝟐. 𝟎𝟕𝟗 = 𝟎. 𝟔𝟑𝟏
𝟖
152
c. Find 𝑙𝑜𝑔𝑎 (
𝒍𝒐𝒈𝒂 (
√8
𝟏𝟓𝟐
√𝟖
) if 𝑙𝑜𝑔𝑎 15 = 2.71 and 𝑙𝑜𝑔𝑎 8 = 2.079
) = 𝟑𝒍𝒐𝒈𝒂 (
𝟏𝟓𝟐
√𝟖
)
𝟏
= 𝟑 𝒍𝒐𝒈𝒂 𝟏𝟓𝟐 − 𝒍𝒐𝒈𝒂 𝟖𝟐
= 𝟑 𝟐𝒍𝒐𝒈𝒂 𝟏𝟓 −
𝟏
𝒍𝒐𝒈𝒂 𝟖
𝟐
𝟏
= 𝟑 𝟐(𝟐. 𝟕𝟏) − (𝟐. 𝟎𝟕𝟗)
𝟐
= 𝟏𝟑. 𝟏𝟒𝟏𝟓
Exponential and Logarithmic Equations
 Solving Exponential Equations Using Logarithmic Forms
To solve an exponential equation using logarithmic form:
1. Rewrite the equation with the term containing the exponent by itself on one side.
2. Divide both sides by the coefficient of the term containing the exponent.
3. Change the new equation to logarithmic form.
4. Solve for the variable.
EX) Solve the equation 3000 = 150(1014𝑡 ) for t by converting it to logarithmic form.
1. The term containing the exponent is by itself on one side of the equation.
2. We divide both sides of the equation by 150.
𝟑𝟎𝟎𝟎 = 𝟏𝟓𝟎(𝟏𝟎𝟒𝒕 )
𝟐𝟎 = 𝟏𝟎𝟒𝒕
3. We rewrite this equation in logarithmic form.
𝟒𝒕 = 𝒍𝒐𝒈𝟏𝟎 𝟐𝟎 or 𝟒𝒕 = 𝐥𝐨𝐠 𝟐𝟎
4. Solving for t gives the solution:
𝒕=
𝐥𝐨𝐠 𝟐𝟎
≈ 𝟎. 𝟑𝟐𝟓𝟐𝟔
𝟒
 Change of Base Formula
If 𝑏 > 0, 𝑏 ≠ 1, 𝑎 > 0, 𝑎 ≠ 1, and 𝑥 > 0, then
𝒍𝒐𝒈𝒂 𝒙 =
𝒍𝒐𝒈𝒃 𝒙
𝒍𝒐𝒈𝒃 𝒂
In particular, for base 10 and base e,
𝒍𝒐𝒈𝒂 𝒙 =
𝐥𝐨𝐠 𝒙
𝐥𝐨𝐠 𝒂
and
𝒍𝒐𝒈𝒂 𝒙 =
𝐥𝐧 𝒙
𝐥𝐧 𝒂
 Solving Exponential Equations Using Logarithmic Properties
To solve an exponential equation using logarithmic properties:
1. Rewrite the equation with a base raised to a power on one side
2. Take the logarithm, base e or 10, of both sides of the equation.
3. Use a logarithmic property to remove the variable from the exponent.
4. Solve for the variable.
EX) Solve the following exponential equations:
a. 4096 = 82𝑥
1. This equation has the base 8 raised to a variable power on one side
2. Taking the logarithm, base 10, of both sides of the equation 𝟒𝟎𝟗𝟔 = 𝟖𝟐𝒙 gives
𝐥𝐨𝐠 𝟒𝟎𝟗𝟔 = 𝐥𝐨𝐠 𝟖𝟐𝒙
3. Using the Power Property of Logarithms removes the variable x from the exponent:
𝐥𝐨𝐠 𝟒𝟎𝟗𝟔 = 𝟐𝐱 𝐥𝐨𝐠 𝟖
4. Solving for x gives the solution.
𝐥𝐨𝐠 𝟒𝟎𝟗𝟔
=𝒙
𝟐 𝐥𝐨𝐠 𝟖
𝒙=𝟐
b. 6(43𝑥−2 ) = 120
1. We first isolate the exponential expression on one side of the equation by dividing both sides by 6.
𝟔 𝟒𝟑𝒙−𝟐
𝟏𝟐𝟎
=
𝟔
𝟔
𝟒𝟑𝒙−𝟐 = 𝟐𝟎
2. Taking the natural logarithm of both sides leads to the solution.
𝐥𝐧 𝟒𝟑𝒙−𝟐 = 𝐥𝐧 𝟐𝟎
(𝟑𝐱 − 𝟐) 𝐥𝐧 𝟒 = 𝐥𝐧 𝟐𝟎
𝟑𝒙 − 𝟐 =
𝟑𝒙 =
𝐥𝐧 𝟐𝟎
𝐥𝐧 𝟒
𝐥𝐧 𝟐𝟎
+𝟐
𝐥𝐧 𝟒
𝐥𝐧 𝟐𝟎
+𝟐
𝒙 = 𝐥𝐧 𝟒
≈ 𝟏. 𝟑𝟖𝟕
𝟑
Exponential Functions and Investing
 Future Value of an Investment with Annual Compounding
If $P is invested at an interest rate r per year, compounded annually, the future value S at the end of t
years is
𝑺 = 𝑷(𝟏 + 𝒓)𝒕
 Future Value of an Investment with Periodic Compounding
If $P is invested for t years at the annual interest rate r, where the interest is compounded k times per
𝑟
years, then the interest rate per period is 𝑡 , the number of compounding periods if kt, and the future value
that results is given by
𝒓 𝒌𝒕
𝑺 = 𝑷 (𝟏 + ) dollars
𝒕
EX) a. Write the equation that gives the future value of $1000 invested for t years at 8% compounded annually.
Substituting 𝑷 = 𝟏𝟎𝟎𝟎 and 𝒓 = 𝟎. 𝟎𝟖 in 𝑺 = 𝑷(𝟏 + 𝒓)𝒕 gives
𝑺 = 𝟏𝟎𝟎𝟎(𝟏 + 𝟎. 𝟎𝟖)𝒕 or 𝑺 = 𝟏𝟎𝟎𝟎(𝟏. 𝟎𝟖)𝒕
b. Write the equation that gives the future value of $1000 invested for t years at 8% compounded daily.
𝒓 𝒌𝒕
Substituting 𝑷 = 𝟏𝟎𝟎𝟎 and 𝒓 = 𝟎. 𝟎𝟖, and 𝒌 = 𝟑𝟔𝟓 in 𝑺 = 𝑷 (𝟏 + )
𝒕
𝑺 = 𝟏𝟎𝟎𝟎 (𝟏 +
gives
𝟎. 𝟎𝟖 𝟑𝟔𝟓𝒕
)
𝟑𝟔𝟓
 Future Value of an Investment with Continuous Compounding
If $P is invested for t years at an annual interest rate r compounded continuously, then the future value S
is given by
𝑺 = 𝑷𝒆𝒓𝒕 dollars
EX) a. What is the future value of $2650 invested for 8 years at 12% compounded continuously?
The future value of this investment is 𝑺 = 𝟐𝟔𝟓𝟎𝒆𝟎.𝟏𝟐(𝟖) = 𝟔𝟗𝟐𝟏. 𝟎𝟎 dollars
b. How much interest will be earned on this investment?
The interest earned on this investment is the future value minus the original investment:
$𝟔𝟗𝟐𝟏 − $𝟐𝟔𝟓𝟎 = $𝟒𝟐𝟕𝟏
Annuities; Loan Repayment
 Future Value of an Ordinary Annuity
If R dollars are contributed at the end of each period for n periods into an annuity that pays interest at rate
i at the end of the period, the future value of the annuity is
𝑺 = 𝑹[
(𝟏 + 𝒊)𝒏 − 𝟏
]
𝒊
EX) Find the 5-year future value of an ordinary annuity with a contribution of $500 per quarter into an account that pays 8% per year
compounded quarterly.
𝟎.𝟎𝟖
The payments and interest compounding occur quarterly, so the interest rate per period is
= 𝟎. 𝟎𝟐 and the number of
𝟒
compounding periods is 𝟒(𝟓) = 𝟐𝟎. Substituting the information into the formula for the future value of an annuity gives
𝑺 = 𝟓𝟎𝟎 [
(𝟏 + 𝟎. 𝟎𝟐)𝟐𝟎 − 𝟏
] = 𝟏𝟐, 𝟏𝟒𝟖. 𝟔𝟖
𝟎. 𝟎𝟐
Thus, the future value of this investment is $12,148.68
 Present Value of an Ordinary Annuity
If a payment of $R is to be made at the end of each period for n periods from an account that earns
interest at a rate of i per period, then the account is an ordinary annuity, and the present value is
𝑨 = 𝑹[
𝟏 − (𝟏 + 𝒊)−𝒏
]
𝒊
EX) A couple who wants to purchase a home has $30,000 for a down payment and wants to make monthly payments of $2200. If the
interest rate for a 25-year mortgage is 6% per year on the unpaid balance, what is the price of a house they can buy?
The amount of money that they can pay for the house is the sum of the down payment and the present value of the payments that
𝟔%
𝟎.𝟎𝟔
they can afford to pay. The present value of the 𝟏𝟐(𝟐𝟓) = 𝟑𝟎𝟎 monthly payments of $2200 with interest at
=
= 𝟎. 𝟎𝟎𝟓
𝟏𝟐
Per month is
𝑨 = 𝟐𝟐𝟎𝟎 [
𝟏 − (𝟏 + 𝟎. 𝟎𝟎𝟓)−𝟑𝟎𝟎
] = 𝟑𝟒𝟏, 𝟒𝟓𝟓. 𝟏𝟎
𝟎. 𝟎𝟎𝟓
They can buy a house costing $341,455 + $30,0000 = $371,455.10
𝟏𝟐
 Amortization Formula
If a debt of $A, with interest at a rate of i per period, is amortized by n equal periodic payments made at
the end of each period, then the size of each payment is
𝑹=𝑨
𝒊
𝟏 − (𝟏 + 𝒊)−𝒏
EX) A couple that wants to purchase a home with a price of $230,000 has $50,000 for a down payment. If they can get a 25-year
mortgage at 9% per year on the unpaid balance,
a. What will be their equal monthly payment?
The amount of money that they must borrow is $230,000 - $50,000 = $180,000.
The number of monthly payments is 12(25) = 300, and the interest rate is
payment is
𝑹 = 𝟏𝟖𝟎, 𝟎𝟎𝟎
𝟗%
𝟏𝟐
=
𝟎.𝟎𝟗
𝟏𝟐
= 𝟎. 𝟎𝟎𝟕𝟓 per month. The monthly
𝟎. 𝟎𝟎𝟕𝟓
≈ 𝟏𝟓𝟏𝟎. 𝟓𝟓𝟑
𝟏 − (𝟏 + 𝟎. 𝟎𝟎𝟕𝟓)−𝟑𝟎𝟎
so the required payment would be $1510.55
b. What is the total amount they will pay before they own the house outright?
The amount that they must pay before owning the house is the down payment plus the total of the 300 payments:
$50,000 + 300($1510.55) = $503,168
c. How much interest will they pay?
The total interest is the total amount paid minus the price for the house. The interest is
$503,168 - $230,000 = $273,168