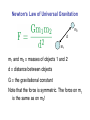Download Early Astronomy and Gravity

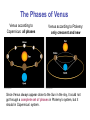
Reminders!
Website: http://starsarestellar.blogspot.com/
Lectures 1-5 are available for download as study aids.
Reading: You should have Chapters 1-4 read, Chapter 5
by the end of today, and Chapters 6 and 7 by the end of
this weekend.
Homework: You should have homework #1 turned in
already. Homework #2 is due next Wednesday.
Discussion: Next week, we’ll review for the midterm.
Remember you can attend ANY discussion section. The
schedule is Monday 1-2, Tuesday 1-2, Wednesday 9-10,
all in Evans 264.
Observing Project
Remember that for one of your observing projects you can
go to a star party (stargazing).
This is available at the Lawrence Hall of Science every 1st and
3rd Saturday of the month. For more information (be sure to call
ahead) see:
http://lawrencehallofscience.org/visit/exhibits/stargazing
Also: The Chabot Space & Science Center has stargazing
every Friday and Saturday 7:30-10:30. This can also count for
your star party observing project.
This Saturday, there will be a special lecture (James Allen
Telescope Array - ATA) and star party, starting at 7:30 pm.
Chabot Space & Science Center:
http://www.chabotspace.org/visit/observatories.aspx
East Bay Astronomical Society: http://www.eastbayastro.org/
Early Astronomy and Gravity
Today’s Lecture:
• Review from yesterday (chapter 5, pages 90-102)
Early astronomy, Copernicus, Galileo
• Kepler and Newton (chapter 5, pages 103-109)
Kepler’s 3 Laws
Newton’s Laws of Motion
The Solar System
Early history of Solar System Studies (Greece)
• Planets wander slowly (over
many weeks) among the “fixed
stars.” (This is NOT to be
confused with the daily east-towest movement due to the
Earth’s rotation.)
Earth
• Usually the planets drift from
west to east.
• It is natural (but incorrect) to
think of the Earth as the center
of the Universe
• Spheres for each planet, the
Moon, the Sun, and the stars
seem to rotate around it.
S
Stars embedded in
the celestial sphere
Retrograde Motion
• Retrograde motion is a problem for the simplest geocentric models.
• Each year, planets drift from east to west for a while!
E
W
E
W
• Ptolemy (~140 AD) devised a new geocentric theory to explain this.
From Ptolemy to Copernicus
• Ptolemy’s geocentric system was very complicated, but also very
accurate. It lasted for nearly 1500 years!
• But most people still thought that the “perfect reality” was a bunch
of “nested spheres” as Aristotle originally suggested.
• Copernicus wrote about
heliocentric theory, first
published in 1543 (after
death)
• Galileo’s used a telescope
to see that Venus goes
through an entire set of
phases (like the Moon)
confirming the heliocentric
hypothesis (1610)
The Phases of Venus
Venus according to
Copernicus: all phases
Venus according to Ptolemy:
only crescent and new
Since Venus always appear close to the Sun in the sky, it could not
go through a complete set of phases in Ptolemy’s system, but it
should in Copernicus’ system.
Tycho Brahe
• He saw a partial solar
eclipse at age 14 and was
impressed by the
prediction.
• He decided to measure
very accurate positions of
planets (especially Mars)
for 20 years.
• Hired Johannes Kepler,
a superb mathematician,
to analyze the data.
Johannes Kepler
• He analyzed Tycho’s data.
• Revised the Copernican system with 3 laws:
1. Planetary orbits are ellipses (and NOT circles), with the Sun
at one focus (nothing at the other focus)
2. A line between the Sun and a planet sweeps out equal
areas in equal times
3. The square of a planet’s orbital period is proportional to the
cube of its semimajor axis
P2 ∝ R3 or
P2 = kR3, where k = some constant
• These laws were purely empirical; Kepler had no physical
explanation for them.
Information on ellipses
Eccentricity: e = (distance between foci) / (major axis)
If both foci are at the same point, then it’s a circle and e = 0.
The maximum value is e=1, which makes a long, skinny ellipse.
e=0
e = 0.5
e = 0.9
P
Ellipse: set of points P
such that a + b = constant
a
Sun
Kepler’s 1st Law: Move
on ellipses with on the
Sun at one focus.
Kepler’s 2nd Law: Equal
areas are swept by the
planets in equal time
(planets go faster when
closer to the Sun).
b
t2
t1
Each sector in this ellipse has
the same area, thus t1 = t2
Kepler’s 3rd Law
P2 ∝ R3
or
P2 = kR3 where k is a constant
It’s convenient to use units based on the Earth’s orbit!
Example:
or
Pearth = 1 year and Rearth = 1 Astronomical Unit (A. U.)
If Pmars = 1.88 years, then what is Rmars?
Rmars = (1.88)2/3 = 1.52 A.U.
Isaac Newton (1642-1727)
1661 Goes to Cambridge University
1665 Flees Cambridge due to the plague. Invents
calculus, discovers universal law of gravitation,
develops laws of motion, begins studies of optics.
1669 Becomes Lucasian Professor of Mathematics
1671 Invents the reflecting telescope.
1687 Publishes The Principia.
1693 Goes temporarily insane
1696 Becomes Warden of the Mint.
1704 Publishes Opticks
1705 Knighted (for service to the government)
Isaac Newton
“The Principia” (1687)
Three Laws of motion:
(1) If no forces act on a body, its speed and
direction of motion stay constant
(2) Force = mass x acceleration
or
F = ma
(Note: acceleration is the change in speed OR
direction of motion)
(3) When two bodies interact, they each exert equal
and opposite forces on each other.
Newton’s Law of Universal Gravitation
m2
d
m1
m1 and m2 = masses of objects 1 and 2
d = distance between objects
G = the gravitational constant
Note that the force is symmetric. The force on m1
is the same as on m2!
Cannon ball thought
experiment
How does gravity produce orbits?
I. No gravity:
III. I + II
Straight line motion at
constant speed.
Constant tangent speed plus
gravity gives an orbit!
Imagine many
small steps
II. Gravity:
Body starts from rest
and accelerates due
gravity to velocity
v = at in a time t
v
An orbit = fall and miss
The Moon is constantly
falling toward the
Earth…it just keeps
missing! (that’s good,
right?)
m2
m1
No m2!
This shows that the
acceleration of an object
acted on by gravity is
independent of its mass!
Newton derives Kepler’s Laws!
• From his laws of motion and universal
gravitation, Newton derived and generalized
Kepler’s three empirical laws.
(1) Orbits in general are conic sections which
depend on the transverse velocity. If bound, it will be
an ellipse or circle, but it can easily be a hyperbola
or parabola.
(2) A planet sweeps out equal areas in equal times:
property of gravity being strongest when the
distance is smallest (difficult to derive simply).
Conic sections
and orbits
Newton derives Kepler’s Laws! (cont.)
(3) Combining Newton’s 2nd law of motion with
gravitation and assuming a circular orbit:
Before Kepler derived his law for things orbiting the
Sun. This new law applies for everything (for
example, the moon of Jupiter).
is nearly constant if m1 >> m2
Newton calculates the Sun’s mass!
• IMPORTANT: If m1 >> m2, then we can ignore m2
so
If we can measure P and R, then we can derive m1!
Example: What is the Sun’s mass?
Plug in numbers ---->
Msun = 2 x 1033 grams!
We can also estimate the mass of the Earth from
the Moon!
Orbital Speeds of Planets
• For any planet:
• If the orbit is roughly circular, then
2πR = VP
(distance = speed x time)
This shows that distant planets should move more
slowly (also related to Kepler’s 2nd law)