* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Domain Restrictions
Abuse of notation wikipedia , lookup
Law of large numbers wikipedia , lookup
Large numbers wikipedia , lookup
Functional decomposition wikipedia , lookup
Principia Mathematica wikipedia , lookup
Big O notation wikipedia , lookup
Continuous function wikipedia , lookup
Dirac delta function wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
History of the function concept wikipedia , lookup
Non-standard calculus wikipedia , lookup
Function (mathematics) wikipedia , lookup
22
Instruction: Domain
In functions that map real numbers to real numbers, the independent variable represents domain
values. In practical terms, the possible values of the independent variable, usually denoted by x,
represent the domain.
or in set interval notation as
Many functions have a domain of all real numbers denoted
(−∞, ∞) . Three important functions that we will study do not have a domain of all real numbers.
Rational functions, that is, functions with a variable in the denominator of a rational expression
like r ( x ) below, often have restrictions on their domain.
r ( x) =
x +1
x−2
A rational expression with zero as the divisor is undefined. Consequently, r ( x ) has a limited
domain since r ( x ) cannot be defined when x = 2. Thus, the domain of r ( x ) in set interval
notation is (−∞,2) ∪ (2, ∞). All rational functions have restrictions on their domain. These
restrictions correspond to the x-values that render the denominator equal to zero. To find the
restrictions on a rational function, set the denominator equal to zero and solve.
Similarly, functions with variables in the radicand of a radical with an even index like R ( x )
below sometimes have limited domains:
index
R ( x) = 4 x
radicand
The radicand of even roots such as a square root or fourth root must be non-negative to render a
real number result. Consequently, R ( x ) has a limited domain since R ( x ) does not exist as real
numbers when x < 0. Thus, the domain of R ( x ) in set interval notation is [0, ∞). All functions
with independent variables in the radicand of a radical with an even index have restrictions on
their domain. These restrictions (x-values that are excluded from the domain) correspond to the
x-values that render the radicand negative. To find the domain (included x-values) of a function
containing a radical with an even index, set the radicand greater than or equal to zero and solve.
Logarithmic functions, which we discuss later in the course, also have restricted domains.
Instruction: Range
In a function, the dependent variable represents elements in the co-domain. In practical terms,
the possible values of the dependent variable, usually denoted by y or f ( x ) , represent the range
(the range is always a subset of the co-domain). Determining a function’s range requires some
understanding of the function’s behavior. Consider q ( x ) = x 2 . Since every x-value is squared to
find the value of q ( x ) , the function never has a negative value. Thus, the range in set interval
notation is [0, ∞). The range can readily be ascertained from the function’s graph.
23
q(x)
Since the lowest value of the graph is zero and since the graph approaches infinity on the y-axis
without interruption, the range extends from zero to positive infinity [0, ∞).
Instruction: Increasing/Decreasing/Constant Behavior
A function increases along an interval if the function’s values increase as the values of the
independent variable increase. In other words, if the y-values increase as the x-values increase,
the function increases. Consider the graph of q ( x ) above. The function q ( x ) increases as the
x-values increase beginning with zero and extending forward. Thus, q ( x ) increases along the
interval (0, ∞).
Likewise, a function decreases along an interval if the function’s values decrease as the values of
the independent variable increase. In other words, if the y-values decrease as the x-values
increase, the function decreases. Consider the graph of q ( x ) above. The function q ( x )
decreases as the x-values increase from negative infinity to zero. Thus, q ( x ) decreases along
the interval (−∞,0).
If a function’s value remains unchanged as the x-value changes, the function is constant.
Consider k ( x ) below.
k ( x)
Since the value of k ( x ) never changes, it is a constant function.
24
An Informal Discussion continued. . .
Recall that a function is a special relation between two sets. A set is a collection of objects, and
for our purposes those objects will be numbers and/or amounts. In this class, we will assume that
the domain for our functions is the set of all real numbers noted as
or using set interval
notation ( −∞, ∞ ) . There are some cases outlined below for which the domain will not include all
real numbers.
I.
The domain is stated as some subset of
II.
The operation of the function implies a domain restriction. Two such operations
are division and taking even roots.
III.
The word problem represented by the function implies a restriction.
.
Previously, we discussed the monthly income of a paperboy who earns $4.50 for every subscriber
to whom he delivers the paper. We used the function below to describe the paperboy's monthly
income.
p(x) = $4.50x
Since the "rule" of the function involves multiplication (multiply the domain value by $4.5 to get
the corresponding range value), the operation of the function does not imply a domain restriction.
In other words, since we can multiply any number by 4.5, the domain could be the set of real
numbers, . Our function, however, represents a word problem where x (the domain variable)
represents the number of subscribers. For our word problem, it does not make sense to assume
the paperboy will deliver papers to a negative number of subscribers. In fact, it does not make
sense to include fractions since the paperboy probably will not have fractional number of
subscribers. If we assume that the paperboy can deliver a maximum of 1,000 papers, we might
use descriptive notation and say:
D = {a whole number of subscribers from 0 to 1,000}.
Using set-builder notation where
D = { x | 0 ≤ x ≤ 1, 000, x ∈
indicates the set of integers, we have:
}.
Since the range of our function is the product of $4.5 and each element from the domain, we
have:
R = { y | $0, $4.5, $9, $13.5, $18, … $4,500}
Note that writing the range as a sequence of numbers reveals that p(x) is an increasing function.
25
Instruction: Seven Elementary Functions
Suppose X = Y = . This lecture discusses seven elementary mappings from X to Y . The
serious student will memorize these seven functions.
I. f ( x) = x
As defined in Box I, f is a linear function. The function increases throughout its domain,
which includes all real numbers. The range also includes all real numbers. Since the range equals the
co-domain, f is surjective. Since the graph passes the horizontal line test, is
injective. Being both
surjective and injective makes f a bijective function.
x
–2
–1
0
1
2
f(x)
–2
–1
0
1
2
II. A( x) = x
As defined in Box II, A is an absolute value function. It decreases from negative infinity to
zero (– ∞ ,0) and increases thereafter (0, ∞ ). The function is symmetrical about the y-axis. The
minimum value of g is zero, so the range is (0, ∞ ). Since the range does not equal the co-domain, this
function is not surjective. Since it does not pass the horizontal line test, A is not injective.
x
A( x)
–2
–1
0
1
2
2
1
0
1
2
26
III. q ( x) = x 2
As defined in Box III, q is a quadratic function with a vertex at the origin (0,0). The function
decreases from negative infinity to zero (– ∞ ,0) and increases thereafter (0, ∞ ). Thus, the y-value of the
vertex represents the absolute minimum value of the function, and the range is (0, ∞ ). The function is
symmetrical about the y-axis. Since the range of the function does not equal the co-domain, q is not
surjective. Since the graph of the function fails the horizontal line test, q is not injective.
x
q ( x)
–2
–1
0
1
2
4
1
0
1
4
IV. s ( x) = x
As defined in Box IV, s is a square root function. When mapping to real numbers, taking the
square root implies a restriction on the domain. The domain of s is limited to where the radicand is
positive; thus, the domain is where x > 0. The function increases throughout its domain. The minimum
value of s is zero, so the range is (0, ∞ ). Since the range does not include all real numbers, s is not
surjective. Since the graph passes the horizontal line test, s is injective.
x
s ( x)
–1
non-real number
(not in domain)
0
1
2
2
0
1
2
4
27
V. c( x) = x 3
As defined in Box V, c is a cubic function. The domain and range both include all real
numbers. Since the range equals the co-domain, c is surjective. It is also injective.
x
–2
–1
0
1
2
c( x )
–8
–1
0
1
8
VI. y ( x) = 3 x
As defined in Box VI, y is a cube-root function. The domain and range both include all real
numbers. Since the range equals the co-domain, y is surjective. It is also injective.
x
–8
–2
–1
0
1
2
8
y(x)
–2
−3 2
–1
0
1
3
2
2
1
VII. r ( x) =
x
As defined in Box VII, r is the reciprocal function. Since zero does not have a reciprocal, the
operation of function implies a restriction on the domain, namely, zero. The domain includes all real
28
numbers except zero, ( −∞, 0 ) ∪ ( 0, ∞ ) . The range also excludes zero because no number divides into
one zero times. Since the range does not include all real numbers, r is not surjective. The graph of r
passes the horizontal line test, so r is injective. The reciprocal function exhibits asymptotic behavior,
something discussed hereafter.
x
–2
–1
–½
0
½
1
2
r(x)
–½
–1
–2
0
2
1
½
Instruction: Asymptotic Behavior
When the graph of a function mimics a line, we say the function exhibits asymptotic behavior.
Defining mimicry requires concepts taught in calculus, but we can begin the discussion here. Let’s
start with oblique and horizontal lines.
Let l be an oblique or horizontal line in the Cartesian plane. Let f be a function. Suppose we
travel further and further in some direction along l and find the graph of f getting closer and closer to
l . Suppose also that for any given positive distance however small, there is some point along the line
where thereafter f is at least that close to l . Then, we say l is an asymptote of f . Note that the
function f might cross back and forth over l but still get closer the further we travel along l .
1
The line y = 0 is an asymptote of the reciprocal function r ( x ) = . Choose any measure of
x
1
proximity, say ε . Then, when x > , the graph of the reciprocal function will be within ε -units of
ε
y = 0 . In particular, let ε = 0.0001 . Then, when x > 10, 000 , r ( x ) is no more than 0.0001 units from
zero.
Vertical lines can also be asymptotes of a function. Suppose x = a is a vertical line in the
Cartesian plane. If the graph of f gets ever further from zero as the corresponding x -values get ever
closer to a and if there is no limit to how far from zero the graph of f will go, then we say x = a is a
vertical asymptote of the function.
When a line is an asymptote of a function, we say the function exhibits asymptotic behavior.
29
Instruction: Piecewise Functions
⎧ x 3 if x < 0
⎪
p ( x) = ⎨
⎪ x + 1 if x ≥ 0.
⎩
Piecewise functions are functions whose definition involves more than one formula. For
example, consider p(x) above.
Since p(x) is defined by two formulas [p(x) = x3 for x-values below zero and p(x) = x + 1 for xvalues greater than or equal to zero], it is a piecewise function. When generating its table of
ordered pairs, substitute values less then zero into x3 and values equal to or greater than zero into
x + 1. Since the first piece of the function has values corresponding to x-values that approach
zero, it may be helpful to substitute zero for x in the first formula just to determine an endpoint of
the first piece. The graph should have an open circle at this end-point unless it corresponds to
the beginning point of the next piece of the function.
x
-2
-1
0
0
1
2
p(x) = x3
-8
-1
0 (not a value of the function)
p(x) =x + 1
1
2
3
30
An Informal Discussion continued. . .
Previously, we discussed the monthly income of a paperboy who earns $4.50 for every subscriber
to whom he delivers the paper. We used the function below to describe the paperboy's monthly
income.
p(x) = $4.50x
Sometimes, real-world functions are much more complicated. For instance, let's consider the
paperboy's weekly income (instead of his monthly income) assuming that he gets paid per hour of
work (instead of per subscriber serviced). In the real world, the paperboy would earn more per
hour if he worked more than forty hours per week. Let's assume he averages $6.00 per hour if he
works more than forty hours in the week and that he cannot work more than eighty hours
according to company policy. According to these assumptions, we can represent the paperboy's
weekly income with a piece-wise function given below.
⎧$4.50 x
P( x) = ⎨
⎩$6.00x
if 0 ≤ x ≤ 40
if 40 < x ≤ 80
Recall that a function only assigns one y-value to any given x-value. Accordingly, when we try
to evaluate P(20) and P(50), we must ask ourselves, "Which rule must be used?" In this case, we
either multiply the x-value by $4.50 or by $6.00. For P(20) where the input value is twenty, we
multiply by $4.50 because that is the rule for x-values from zero to forty. For P(50) where the
input value is fifty, we multiply by $6.00 because that is the rule for x-values greater than forty
but less than or equal to eighty. Thus, P(20) = $90.00 and P(50) = $300.00.
We might also note that our piece-wise function has a stated domain. The "if statements"
represent "pieces" of the domain, and all the "if statements" taken together give the full domain.
The domain of P(x) in our discussion includes all the real numbers from zero to eighty, written in
set interval notation as [0,80].
31
Instruction: Domain, Range, Behavior
Example 1
Stating the Domain of a Function
Given f ( x ) = 5 + −1 − x , what is the domain of f ( x) ?
The domain is understood to be all real numbers unless the operation implies a
restriction. This function implies a restriction because taking the even root of a number
only produces a real number result if the number is a non-negative number. To find the
domain, find where the radicand is non-negative.
−1 − x ≥ 0
−1 − x + x ≥ 0 + x
−1 ≥ x
x ≤ −1
The x-values must be less than or equal to negative one. Using set interval notation, the
domain is ( −∞, −1] . The bracket next to negative one indicates that negative one is part
of the domain.
Example 2
Stating the Domain of a Function
Given Q( x) =
x +1
, what is the domain of Q( x) ?
x − 6 x − 16
2
The domain is understood to be all real numbers unless the operation implies a
restriction. Q(x) implies a restriction because division by zero is undefined. To find the
domain, find where the denominator does not equal zero.
x 2 − 6 x − 16 ≠ 0
( x + 2 )( x − 8) ≠ 0
x + 2 ≠ 0, x − 8 ≠ 0
x ≠ −2,
x≠8
The x-values may take any value except –2 and 8. The domain has three intervals of
values: all the numbers less than –2, the numbers between –2 and 8, and all the
numbers greater than 8; thus, D = ( −∞, −2 ) ∪ ( −2,8 ) ∪ ( 8, ∞ ) .
32
Example 3
Stating the Domain of a Function
Given s ( x ) = x 2 + 2 x + 1 , what is the domain of s(x)?
The domain is understood to be all real numbers unless the operation implies a
restriction. The operations involved with s(x) do not imply a restriction. Any number
can be multiplied by itself. Any number can be doubled, and any two numbers can be
added together and added to one. The domain of s(x) includes all real numbers denoted
by
or written in set interval notation as ( −∞, ∞ ) .
Example 4
Finding the Range of a Function
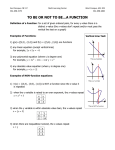
What is the range of the function graphed below?
The range is the set of values assigned to correspond with the domain values. The
vertical axis represents the range values. Identifying the range involves finding the lowest
value and the highest value of the function and noticing any breaks in between. The
graph above shows a function that is continuous--that is, it does not have any breaks-along a domain of [0,24]. The lowest value of 600 megawatts occurs during the fourth
hour and twenty-fourth hour. The highest value of 1,400 megawatts occurs during the
sixteenth hour. The range extends from 600 to 1,400. Using set interval notation, the
range is [ 600,1400] . The brackets indicate that 600 and 1,400 are both included in the
range.
33
Example 5
Recognizing Behavior
Given F(x) = (x – 3)4, for what value of x does the F(x) change behavior?
Behavior refers to whether or not the function's values decrease, remain constant, or
increase as x-values increase. Examining a table of values of the function for increasing
x-values helps determine the behavior. Arbitrarily pick some x-value, below negative
eight is chosen, and then increasing x-values. Look for a change in behavior.
x
–8
–6
–4
–2
0
2
4
(x – 3)4
F(x)
14,641
( −8 − 3)
4
( −6 − 3)
4
( −4 − 3)
4
( −2 − 3)
4
( 0 − 3)
4
( 2 − 3)
4
( 4 − 3)
4
6,561
2,401
625
81
1
1
The function decreased until two, then a change seemed to have occurred. Choosing xvalues closer together may help determine what happens between two and four.
x
2
2.5
3
3.5
4
(x – 3)4
( 2 − 3)
F(x)
1
4
( 2.5 − 3)
4
( 3 − 3)
4
( 3.5 − 3)
4
( 4 − 3)
4
0.0625
0
0.0625
1
This exercise helps make it clear that as x-values increased from negative numbers (with
large absolute values) to x-values close to three, the function decreases, but the function
starts increasing thereafter.
The function changes behavior from decreasing to increasing at x = 3.
34
Instruction: Elementary Functions
Example 1
Elementary Functions
Name the function graphed below.
The function is a quadratic function, y = x 2 .
Example 2
Elementary Functions
Name the function graphed below?
The function is the linear function f ( x) = x .
Example 3
Elementary Functions
State the domain of y = x .
The radicand of a square root must be a non-negative value. The domain of the square
root function includes non-negative numbers: [ 0, ∞ ) .
35
Example 4
Elementary Functions
State the range of A( x) = x .
The absolute value of a non-zero number is positive. The absolute value of zero is zero.
The range of the absolute value function is [ 0, ∞ ) .
Example 5
Elementary Functions
Consider the cubic function C ( x) = x 3 . Is the function bijective?
The range of C ( x ) equals all real numbers, so the function is surjective. The graph of
C ( x ) passes the horizontal line test, so the function is injective. Since it is both
surjective and injective, C ( x ) is bijective.
Example 6
Asymptotic Behavior
1
. Find N such that when x > N , the graph of r will be within
x
0.0000025 units of zero.
Suppose r ( x ) =
The horizontal line y = 0 is an asymptote of r because for any positive value ε when
1
x = , the graph of r is within ε units of zero.
ε
If ε = 0.0000025 =
25
1
1
=
, then = 400, 000 .
10, 000, 000 400, 000
ε
Answer: Let N = 400, 000 .
36
Instruction: Piece-wise Functions
Example 1
Evaluating Piece-wise Functions
⎧− x − 1
Consider f ( x ) = ⎨
⎩2 x
if x < 0
. Which is greater f (1 2 ) or f ( −3) ?
if x ≥ 0
Evaluate f (1 2 ) . Note that 1 2 > 0 , and use the "piece" for x-values greater than zero.
f (1 2 ) = 2 (1 2 ) = 1
Evaluate f ( −3) . Note that −3 < 0 , and use the "piece" for the x-values less than zero.
f ( −3) = − ( −3) − 1 = 3 − 1 = 2
Since f (1 2 ) = 1 and f ( −3) = 2 , f ( −3) > f (1 2 ) .
Example 2
Graphing Piece-wise Functions
⎧− x if x < 0
Consider P( x) = ⎨
. Sketch the graph of P(x).
if x ≥ 0
⎩0
The function P(x) has two "pieces" so-to-speak, meaning it has two rules. One rule states that
the function's range value is the opposite of any x-value less than zero. For instance if x = –4,
then y = 4. If x = –3, then y = 3. If x = –2, then y = 2 and so on until the x-values reach zero
where the second rule applies.
For x-values equal to zero or greater, the rule states that the function's range value is zero for any
x-value greater than or equal to zero. For instance, if x = 0, then y = 0, and if x = 4, then y = 0.
The graph of the "piece" for x-values less than zero is linear. The function decreases by one for
every single-unit increase in x (i.e., it has a slope of negative one). The graph of the "piece" for
x-values equal to or greater than zero is constant, which is a horizontal line along the x-axis.
37
Suggested Homework from Blitzer
Section 2.2:
#1-9 odd, #35 a, #35b, #37, #41, #47, #51
Application Exercise
The period in seconds of a pendulum operating at sea level is a function of the length
of the pendulum in meters.
P:l
2
l
9.81
Give a realistic domain and realistic range for the function. Describe the behavior of
the function (in terms of whether it increases or decreases). Determine to which of
our seven elementary functions this function is related.
Mathematical Exercise
A Mersenne prime is a prime number of the form 2 p 1 where p is itself a prime
number. Suppose
is a function that maps prime numbers to Mersenne prime
numbers. In symbols, Π : p 2 p 1. Does the function have any domain
restrictions less than twenty? In other words, are there any primes p less than twenty
such that 2 p 1 is not prime?
38
Problems
State the domain of each of the following functions.
#1 a( x ) x 3
#2 b( x )
x
x 1
#3 c( x) 3 3x 1
#4 d ( x) 4 x
#5 g ( x)
x
x 8
#6 Q( x)
x 2 x 12
x 2 x 56
Graph the piece-wise functions below.
x2
#7 p( x )
4
x 1
#8 P( x )
x 1
if 2 x 2
if x 2 or x 2
if x 2
if x 2
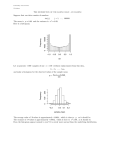
Use the graph of f below to describe the behavior of the function.
#9 What are the intervals of increasing behavior?
#10 What are the intervals of decreasing behavior?
f
a
#1 3,
#5 ,8
#9 , a
#3 ,
8,
0,
#7