Download Ch. 5 Notes.jnt

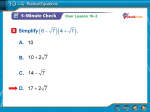
Pre-Calculus 11
Date: _______________
5.0 – Perfect squares and Perfect Cubes
A fast and efficient way to solve radicals is to recognize and know the ‘perfect’ numbers.
Perfect Squares
Perfect Cubes
12
22
13
23
32
33
42
43
52
53
62
63
72
73
82
83
92
93
102
103
112
122
1
132
3
23
142
2
152
3
33
162
3
3
43
172
182
4
192
3
53
20 2
5
212
6
22 2
7
232
8
24 2
9
252
10
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
3
3
3
3
3
3
Page 1 of 29
Pre-Calculus 11
Date: _______________
5.1a – Working with Radical Numbers
Definition:
Radical
Index
Radicand
n
x
Recap: Exponent Laws
(a b) 2
2
a
b
x
3
x
Extension of Exponent Laws:
a b
a
b
In General:
na
n
b =n a n b
a na
=
b nb
Recall:
2
Square roots – a number r , is a square root of a number x , if r
x.
Note: A positive number always has two square roots, one positive and one negative, because:
It is impossible to obtain a negative number when a number is squared, therefore the square root of a
negative number is NOT defined.
Notation: radical sign
, denotes the positive square root only.
x means the positive square root of x , where x
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
0.
Page 2 of 29
Pre-Calculus 11
Date: _______________
Example 1: Simplify.
a)
b) – 0.16 =
2 500 =
3
Cube Roots – A number r , is a cube root of a number x , if r
x.
Note: The cube root of a positive number is _________________.
The cube root of a negative number is _________________.
3
x means the cube root of x
Example 2: Simplify. Round to 3 decimal places if necessary.
a)
note:
3
64
b)
3
125
c)
3
21
b)
3
125
is the same as
Higher Roots
An expression of the form n x is a radical, where n is a natural number. If n is even, the expression
represents only the positive root.
Example 3: Simplify.
a)
4
81
Ch. 5 Radical Expressions & Equations
b)
Loo/Lee/Ko
5
32
Page 3 of 29
Pre-Calculus 11
Date: _______________
Entire Radical vs. Mixed Radical
Let’s look examine the radical
:
can be expressed as a mixed radical 2 different Methods
Method A (Prime Factorization)
Method B (Product of radicals)
Example 4: Express each entire radical as a mixed radical (use method B)
a)
b)
c)
d)
Example 5: Express as an entire radical.
a)
b)
Example 6: Without a calculator order the set of numbers from least to greatest.
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 4 of 29
Pre-Calculus 11
Date: _______________
In all the previous examples so far, the radicand has been a constant term. But what if the radicand
contained a variable? Since a variable is representative of a number, we need to ask ourselves if there
are any restrictions to what this number can be given the index of the radical.
Let’s take a look at the radical expression
What are the values for which this expression is defined?
Let us now look at the expression
What are the values for which this expression is defined?
Can the expression be simplified?
Example 7: Determine the variable for which the expressions are defined. Simplify the expressions.
a)
b)
c)
Assignment
Page 278 (min) #1, 2ad, 4, 6bc, 14, (worksheet) 26
(reg) #1 – 4, 6, 14, (worksheet) 26
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 5 of 29
Pre-Calculus 11
Date: _______________
5.1a Homework Worksheet
26. i. Identify the variables for which the expression is defined
ii. Simplify the expression
a)
b)
c)
Ans: 26a)
i.
ii.
b)
i.
ii.
c)
i.
ii.
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 6 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 7 of 29
Pre-Calculus 11
Date: _______________
5.1b – Adding and Subtracting Radicals
Similar to adding and subtracting polynomials or fractions, radicals have their own set of rules to
simplify radicals.
Recall: 1) 3 + 4 =
2)
Think: 3)
You are only allowed to add/subtract polynomials that have like terms.
Similarly when you are add/subtract radicals, you can only do so when you have like radicals.
Like radicals are radicals that have the same index and same radicand.
Similar to the like terms such as question 2) (where we add the coefficients), we add the numbers that
are in front of the radical signs.
Example 1: Simplify.
a)
b) 6 7 2 7 4 7
3 2 3
c) 6 2
4 5
In cases where the index and radicand are not the same, we need to simplify the radicals first in order to
see if we have any like radicals to add or subtract.
Example 2: Simplify.
a) 6 27 4 3
c) 2 98
10
b) 4 24 3 54
6 8
4 40
Ch. 5 Radical Expressions & Equations
d)
3
16
2 7 6 28
5 3 54
Loo/Lee/Ko
Page 8 of 29
Pre-Calculus 11
Date: _______________
Some radical expressions contain variables. Before you attempt to add/subtract the expressions, you
must state the values for which the expressions are defined.
Example 3: State the values for which the expression is defined, then simplify.
a)
b)
c)
Example 4: State the values for which the expression is defined, then simplify.
a)
c)
4c
3
16 x 2
4 9c
3
2 54 x 2
Ch. 5 Radical Expressions & Equations
b) 20 x 3 45x
d) 2 20 x 3 3 80 x 3
Loo/Lee/Ko
Page 9 of 29
Pre-Calculus 11
Date: _______________
Example 5: A square is inscribed in a circle. The area of the circle is 40
m2.
a) What is the exact length of the diagonal of the square?
b) Determine the exact perimeter of the square.
Assignment
Page 278 (min) #5cd, 8cd, 9bd, 10bd, 15
(reg) #5, 8 – 10, 15, 19
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 10 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 11 of 29
Pre-Calculus 11
Date: _______________
5.2 – Multiplying and Dividing Radical Expressions
Multiplying Radical Expressions
The rule of multiplying radicals:
a
b
ab , a
Note: The expression 4 5 has the same meaning as 4
0, b 0
5
When multiplying radicals the index must be the same. You will calculate the product of the values
outside the radical sign and the product of the values inside the radical sign.
Example 1: Simplify
a)
b)
c)
3 2x
4 6
When multiplying radical expressions that contain more than one term, we will use the distributive
property or F.O.I.L in order to get rid of the brackets.
Example 2: Expand and simplify
a) 7 3 5 5 6 3
Ch. 5 Radical Expressions & Equations
8 2 5 9 5 6 10
Loo/Lee/Ko
Page 12 of 29
Pre-Calculus 11
Date: _______________
Example 3: Expand and simplify. State any restrictions for the variables.
a)
b)
Dividing Radical Expressions
The rule for dividing radicals:
a
b
a
b
when
,
You can combine two radicals into one or separate 1 radical into 2 separate ones.
Example 4: Simplify.
2 30
a)
3
3
b) 4 24
8 18
c)
9x3
3 3x
IMPORTANT: Radicals must NEVER be left in the denominator.
If there is a radical in the denominator, the method to get rid of them is called to “RATIONALIZE
THE DENOMINATOR”
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 13 of 29
Pre-Calculus 11
Date: _______________
Given the expression: 1
3
If we multiply the numerator and denominator by the radical in the denominator, 3 . The radical
will move to the numerator and the answer will remain the same.
1
3
Example 5: Rationalize the denominator then simplify.
a)
b)
c)
Note: Simplify first, it prevents you from doing more work!
Conjugate of a Binomial Expression: The conjugate of
is (
)
When the denominator of an expression contains two terms with at least one radical sign, in order to
rationalize the denominator, you must multiply both the numerator and denominator by the conjugate
of the denominator.
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 14 of 29
Pre-Calculus 11
Date: _______________
Example 6: Rationalize the denominator. Simplify
a)
11
b)
5 7
Assignment
Page 289, (min) #1be, 2ad, 3bc, 4ad, 5c, 6d, 8c, 10d, 11d, 17
(reg) #1bdef, 2ad, 3bc, 4ade, 5bcd, 6d, 7a, 8c, 10bcd, 11cd, 17
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 15 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 16 of 29
Pre-Calculus 11
Date: _______________
Mid-Unit Activity
1. The area of a rectangle is 16 square units. If the width of the rectangle is
units, determine
the exact value of the perimeter in simplified radical form with a rationalized denominator.
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 17 of 29
Pre-Calculus 11
Date: _______________
2. Determine the exact value of both the area and perimeter of the following isosceles triangle.
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 18 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 19 of 29
Pre-Calculus 11
Date: _______________
5.3 – Radical Equations
Radical Equation: __________________________________________________________________
When solving a radical equation we must first state the restrictions on the variable. Because we are
taking the square root, there are certain values for the variable that will make the radical expression
undefined.
To find the restrictions, knowing that the radicand must be a positive number or zero (radicand
set up an inequality and solve for the variable
,
Extraneous Roots: Solution(s) that may arise when an original equation is altered in order to solve the
equation. Any “roots” that are not part of the domain of the original equation are called extraneous
roots.
To solve a radical equation algebraically:
Step 1: Isolate the radical on one side of the equation. If there are two, isolate the most complex term.
Step 2: Square each side, then solve the equation that results.
(note: If the resulting equation still contains a radical term, repeat steps 1 and 2)
Step 3: Identify extraneous roots and reject them.
Example 1: State the restrictions for , them solve for x .
a)
Ch. 5 Radical Expressions & Equations
b)
Loo/Lee/Ko
Page 20 of 29
Pre-Calculus 11
Date: _______________
Example 2: State the restrictions for , then solve for x .
a)
3x 7
8 0
b) 3
x 1 x
Example 3: State the restrictions for , then solve the equation.
x
x 3 5
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 21 of 29
Pre-Calculus 11
Date: _______________
Example 4: The period, T , seconds, of a pendulum is related to its length, L , in metres. The period is
the time to complete one full cycle and can be approximated with the formula T
2
L
.
10
a) Write an equivalent formula with a rational denominator.
b) The length of the pendulum in the HSBC building in downtown Vancouver is 27 m. How long
would the pendulum take to complete 3 cycles (nearest tenth).
Example 5: The mass, m , in kilograms, that a beam with a fixed width and length can support is
related to its thickness, t , in cetimetres. The formula is t
1 m
, m 0 . If a beam is 4 cm thick,
5 3
what mass can it support?
Assignment
(Min) Page 291, #19ab
(Reg) Page 291, #19ab
Page 301, #4bd, 6c, 7d, 8d, 9cd, 10c, 14, 16,18
Page 301, #4bd, 5, 6bc, 7cd, 8ad, 9bcd, 10bcd, 14, 16,18
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 22 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 23 of 29
Pre-Calculus 11
Date: _______________
Ch. 5 Review
Key Ideas
Restrictions and properties of radical expressions
Simplifying radical expressions
Adding & subtracting radical expressions
Multiplying & Dividing radical expressions
Rationalizing the denominator
Solving Radical equations
Example 1: Determine the values of the variables for which the expression is defined.
a)
a)
b)
c)
Example 2: Simplify the following expressions.
a)
b)
Ch. 5 Radical Expressions & Equations
c)
Loo/Lee/Ko
Page 24 of 29
Pre-Calculus 11
Date: _______________
Example 3: Simplify the following expressions.
a)
b)
c)
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 25 of 29
Pre-Calculus 11
Date: _______________
Example 4: Rationalize the denominator.
a)
b)
c)
d)
Example 5: Determine the values for which the expressions are defined, then solve.
a)
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 26 of 29
Pre-Calculus 11
Date: _______________
Example 5: Determine the values for which the expressions are defined, then solve.
b)
c)
d)
Assignment
Page 304, #1ad, 2cd, 3c, 4ab, 6 (nc), 8, 10bc, 11bc, 13ac, 14 – 17, 18bd, 19ade, 21
Ch. 5 Radical Expressions & Equations
Loo/Lee/Ko
Page 27 of 29
Pre-Calculus 11
Ch. 5 Radical Expressions & Equations
Date: _______________
Loo/Lee/Ko
Page 28 of 29