* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 7 . 1 Interior and Exterior Angles
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Integer triangle wikipedia , lookup
Perceived visual angle wikipedia , lookup
Trigonometric functions wikipedia , lookup
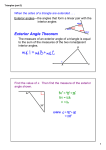
Name Class 7.1 Date Interior and Exterior Angles Essential Question: What can you say about the interior and exterior angles of a triangle and other polygons? Resource Locker Exploring Interior Angles in Triangles Explore 1 You can find a relationship between the measures of the three angles of a triangle. An interior angle is an angle formed by two sides of a polygon with a common vertex. So, a triangle has three interior angles. A Use a straightedge to draw a large triangle on a sheet of paper and cut it out. Tear off the three corners and rearrange the angles so their sides are adjacent and their vertices meet at a point. B What seems to be true about placing the three interior angles of a triangle together? Make a conjecture about the sum of the measures of the interior angles of a triangle. interior angles © Houghton Mifflin Harcourt Publishing Company The conjecture about the sum of the interior angles of a triangle can be proven so it can be stated as a theorem. In the proof, you will add an auxiliary line to the triangle figure. An auxiliary line is a line that is added to a figure to aid in a proof. The Triangle Sum Theorem The sum of the angle measures of a triangle is 180°. B Fill in the blanks to complete the proof of the Triangle Sum Theorem. 4 Given: △ABC Prove: m∠1 + m∠2 + m∠3 = 180° A Statements 1. Parallel Postulate 2. m∠1 = m∠ 2. Module 7 + m∠2 + m∠ 3 C 3. Angle Addition Postulate and definition of straight angle 3. m∠4 + m∠2 + m∠5 = 180° 4. m∠ ℓ 5 Reasons _ 1. Draw line ℓ through point B parallel to AC. and m∠3 = m∠ 1 2 = 180° 4. 313 Lesson 1 Reflect 1. Explain how the Parallel Postulate allows you to add the auxiliary line into the triangle figure. 2. What does the Triangle Sum Theorem indicate about the angles of a triangle that has three angles of equal measure? How do you know? Explore 2 Exploring Interior Angles in Polygons To determine the sum of the interior angles for any polygon, you can use what you know about the Triangle Sum Theorem by considering how many triangles there are in other polygons. For example, by drawing the diagonal from a vertex of a quadrilateral, you can form two triangles. Since each triangle has an angle sum of 180°, the quadrilateral must have an angle sum of 180° + 180° = 360°. A 2 triangles Draw the diagonals from any one vertex for each polygon. Then state the quadrilateral triangle number of triangles that are formed. The first two have already been completed. quadrilateral triangle 1 triangle 2 triangles 1 triangle 2 triangles For each polygon, identify the number of sides and triangles, and determine the angle sums. Then complete the chart. The first two have already been done for you. Polygon Number of Sides Number of Triangles Sum of Interior Angle Measures Triangle 3 1 (1)180° = 180° Quadrilateral 4 2 (2)180° = 360° Pentagon ( ) 180° = Hexagon ( ) 180° = Decagon ( ) 180° = Module 7 314 Lesson 1 © Houghton Mifflin Harcourt Publishing Company B quadrilateral Do you notice a pattern between the number of sides and the number of triangles? If n represents the number of sides for any polygon, how can you represent the number of triangles? Make a conjecture for a rule that would give the sum of the interior angles for any n-gon. Sum of interior angle measures = Reflect 3. In a regular hexagon, how could you use the sum of the interior angles to determine the measure of each interior angle? 4. How might you determine the number of sides for a polygon whose interior angle sum is 3240°? [# Explain 1 Using Interior Angles You can use the angle sum to determine the unknown measure of an angle of a polygon when you know the measures of the other angles. Polygon Angle Sum Theorem The sum of the measures of the interior angles of a convex polygon with n sides is (n – 2)180°. Example 1 A Determine the unknown angle measures. For the nonagon shown, find the unknown angle measure x°. © Houghton Mifflin Harcourt Publishing Company First, use the Polygon Angle Sum Theorem to find the sum of the interior angles: n=9 (n - 2)180° = (9 - 2)180° = (7)180° = 1260° Then solve for the unknown angle measure, x°: 125 + 130 + 172 + 98 + 200 + 102 + 140 + 135 + x = 1260 x = 158 The unknown angle measure is 158°. Module 7 x° 135° 315 125° 98° 130° 102° 140° 200° 172° Lesson 1 B Determine the unknown interior angle measure of a convex octagon in which the measures of the seven other angles have a sum of 940°. n= ( ) Sum = + x= x= ( ) 180° = - 2 180° = The unknown angle measure is . Reflect 5. How might you use the Polygon Angle Sum Theorem to write a rule for determining the measure of each interior angle of any regular convex polygon with n sides? Your Turn 6. Determine the unknown angle measures in this pentagon. x° Determine the measure of the fourth interior angle of a quadrilateral if you know the other three measures are 89°, 80°, and 104°. Module 7 8. 316 Determine the unknown angle measures in a hexagon whose six angles measure 69°, 108°, 135°, 204°, b°, and 2b°. Lesson 1 © Houghton Mifflin Harcourt Publishing Company 7. x° Explain 2 Proving the Exterior Angle Theorem An exterior angle is an angle formed by one side of a polygon and the extension of an adjacent side. Exterior angles form linear pairs with the interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle. Example 2 Remote interior angles Exterior angle Follow the steps to investigate the relationship between each exterior angle of a triangle and its remote interior angles. Step 1 Use a straightedge to draw a triangle with angles 1, 2, and 3. Line up your straightedge along the side opposite angle 2. Extend the side from the vertex at angle 3. You have just constructed an exterior angle. The exterior angle is drawn supplementary to its adjacent interior angle. 2 1 3 4 3 4 Step 2 You know the sum of the measures of the interior angles of a triangle. m∠1 + m∠2 + m∠3 = ° Since an exterior angle is supplementary to its adjacent interior angle, you also know: m∠3 + m∠4 = ° Make a conjecture: What can you say about the measure of the exterior angle and the measures of its remote interior angles? Conjecture: The conjecture you made in Step 2 can be formally stated as a theorem. Exterior Angle Theorem © Houghton Mifflin Harcourt Publishing Company The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles. Step 3 Complete the proof of the Exterior Angle Theorem. 2 ∠4 is an exterior angle. It forms a linear pair with interior angle ∠3. Its remote interior angles are ∠1 and ∠2. 1 By the Also, m∠3 + m∠4 = , m∠1 + m∠2 + m∠3 = 180°. because they are supplementary and make a straight angle. By the Substitution Property of Equality, then, m∠1 + m∠2 + m∠3 = m∠ Subtracting m∠3 from each side of this equation leaves + m∠ . . This means that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles. Module 7 317 Lesson 1 Reflect 9. Discussion Determine the measure of each exterior angle. Add them together. What can you say about their sum? Explain. 60° 40° 10. According to the definition of an exterior angle, one of the sides of the triangle must be extended in order to see it. How many ways can this be done for any vertex? How many exterior angles is it possible to draw for a triangle? for a hexagon? Explain 3 Using Exterior Angles You can apply the Exterior Angle Theorem to solve problems with unknown angle measures by writing and solving equations. Determine the measure of the specified angle. Example 3 A B Find m∠B. Find m∠PRS. Q A 2z° R C (5z - 2)° (x + 2)° P © Houghton Mifflin Harcourt Publishing Company 145° D (3x - 8)° S B Write and solve an equation relating the exterior and remote interior angles. Write an equation relating the exterior and remote interior angles. 145 = 2z + 5z - 2 145 = 7z - 2 Solve for the unknown. z = 21 Now use this value for the unknown to evaluate the expression for the required angle. Use the value for the unknown to evaluate the expression for the required angle. m∠B = (5z - 2)° = (5(21) - 2)° = (105 - 2)° = 103° Module 7 318 Lesson 1 Your Turn Determine the measure of the specified angle. 11. Determine m∠N in △MNP. N 12. If the exterior angle drawn measures 150°, and the measure of ∠D is twice that of ∠E, find the measure of the two remote interior angles. (3x + 7)° D 150° E G (5x + 50)° 63° M F P Q Elaborate 13. In your own words, state the Polygon Angle Sum Theorem. How does it help you find unknown angle measures in polygons? © Houghton Mifflin Harcourt Publishing Company 14. When will an exterior angle be acute? Can a triangle have more than one acute exterior angle? Describe the triangle that tests this. 15. Essential Question Check-In Summarize the rules you have discovered about the interior and exterior angles of triangles and polygons. Module 7 319 Lesson 1 Evaluate: Homework and Practice 1. Consider the Triangle Sum Theorem in relation to a right triangle. What conjecture can you make about the two acute angles of a right triangle? Explain your reasoning. 2. Complete a flow proof for the Triangle Sum Theorem. • Online Homework • Hints and Help • Extra Practice B 4 Given △ABC Prove m∠1 + m∠2 + m∠3 = 180° A 1 2 ℓ 5 3 C Draw ℓ parallel to AC through B. m∠3 = m∠5 m∠4 + m∠2 + m∠5 = Definition of straight angle Alternate Interior Angles Theorem Substitution Property of Equality 3. Given a polygon with 13 sides, find the sum of the measures of its interior angles. 4. A polygon has an interior angle sum of 3060°. How many sides must the polygon have? 5. Two of the angles in a triangle measure 50° and 27°. Find the measure of the third angle. 6. A pentagon has angle measures of 100°, 105°, 110° and 115°. Find the fifth angle measure. Module 7 7. 320 The measures of 13 angles of a 14-gon add up to 2014°. Find the fourteenth angle measure? Lesson 1 © Houghton Mifflin Harcourt Publishing Company Solve for the unknown angle measures of the polygon. 8. Determine the unknown angle measures for the quadrilateral in the diagram. 4x° x° 9. 3x° 2x° The cross-section of a beehive reveals it is made of regular hexagons. What is the measure of each angle in the regular hexagon? 10. Create a flow proof for the Exterior Angle Theorem. 2 © Houghton Mifflin Harcourt Publishing Company ⋅ Image Credits: ©StudioSmart/Shutterstock 1 3 4 Find the value of the variable to find the unknown angle measure(s). 11. Find w to find the measure of the exterior angle. 12. Find x to find the measure of the remote interior angle. x° w° 46° 134° 68° Module 7 321 Lesson 1 14. Determine the measure of the indicated exterior angle in the diagram. 13. Find m∠H. (6x + 1)° H 3x° 126° F G J (3x + 4)° 2x° (5x + 17)° ? 15. Match each angle with its corresponding measure, given m∠1 = 130° and m∠7 = 70°. Indicate a match by writing the letter for the angle on the line in front of the corresponding angle measure. A.m∠2 50° 7 5 B.m∠3 60° 6 C.m∠4 70° D.m∠5 110° 2 3 1 4 E.m∠6 120° 16. The map of France commonly used in the 1600s was significantly revised as a result of a triangulation survey. The diagram shows part of the survey map. Use the diagram to find the measure of ∠KMJ . 70° 88° 48° 17. An artistic quilt is being designed using computer software. The designer wants to use regular octagons in her design. What interior angle measures should she set in the computer software to create a regular octagon? Module 7 322 Lesson 1 © Houghton Mifflin Harcourt Publishing Company 104° ladd er 20° house 18. A ladder propped up against a house makes a 20° angle with the wall. What would be the ladder's angle measure with the ground facing away from the house? ? ground 19. Photography The aperture of a camera is made by overlapping blades that form a regular decagon. a. What is the sum of the measures of the interior angles of the decagon? b. What would be the measure of each interior angle? each exterior angle? c. Find the sum of all ten exterior angles. 20. Determine the measure of ∠UXW in the diagram. Y V © Houghton Mifflin Harcourt Publishing Company ⋅ Image Credits: ©neyro2008/iStockPhoto.com U 78° 54° W X Z 21. Determine the measures of angles x, y, and z. 80° 100° 55° Module 7 x° z° y° 60° 323 Lesson 1 → → 22. Given the diagram in which BD ‾ bisects ∠ABC and CD ‾ bisects ∠ACB, what is m∠BDC? B 15° D A C 24. Algebra Draw a triangle ABC and label the 23. What If? Suppose you continue the congruent angle construction shown here. What polygon will measures of its angles a°, b°, and c°. Draw ray BD you construct? Explain. that bisects the exterior angle at vertex B. Write an expression for the measure of angle CBD. 120° 25. Look for a Pattern Find patterns within this table of data and extend the patterns to complete the remainder of the table. What conjecture can you make about polygon exterior angles from Column 5? Column 2 Sum of the Measures of the Interior Angles Column 3 Average Measure of an Interior Angle Column 4 Average Measure of an Exterior Angle 3 180° 60° 120° 120°(3) = 4 360° 90° 90° 90°(4) = 5 540° 108° 6 © Houghton Mifflin Harcourt Publishing Company Column 1 Number of Sides Column 5 Sum of the Measures of the Exterior Angles 120° Conjecture: Module 7 324 Lesson 1 26. Explain the Error Find and explain what this student did incorrectly when solving the following problem. What type of polygon would have an interior angle sum of 1260°? 1260 = ( n - 2)180 7 = n - 2 5 = n The polygon is a pentagon. H.O.T. Focus on Higher Order Thinking 27. Communicate Mathematical Ideas Explain why if two angles of one triangle are congruent to two angles of another triangle, then the third pair of angles are also congruent. Given: ∠L ≅ ∠R, ∠M ≅ ∠S R L T N S M Prove: ∠N ≅ ∠T © Houghton Mifflin Harcourt Publishing Company 28. Analyze Relationships Consider a right triangle. How would you describe the measures of its exterior angles? Explain. 29. Look for a Pattern In investigating different polygons, diagonals were drawn from a vertex to break the polygon into triangles. Recall that the number of triangles is always two less than the number of sides. But diagonals can be drawn from all vertices. Make a table where you compare the number of sides of a polygon with how many diagonals can be drawn (from all the vertices). Can you find a pattern in this table? Number of Sides, n Number of Diagonals, d Module 7 325 Lesson 1 Lesson Performance Task You’ve been asked to design the board for a new game called Pentagons. The board consists of a repeating pattern of regular pentagons, a portion of which is shown in the illustration. When you write the specifications for the company that will make the board, you include the measurements of ∠BAD, ∠ABC, ∠BCD and ∠ADC. Find the measures of those angles and explain how you found them. A D B C © Houghton Mifflin Harcourt Publishing Company Module 7 326 Lesson 1