* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Math 251: Beginning Algebra Section 4.1 Notes Solving Systems of
Cubic function wikipedia , lookup
Quartic function wikipedia , lookup
Quadratic equation wikipedia , lookup
Elementary algebra wikipedia , lookup
Linear algebra wikipedia , lookup
Signal-flow graph wikipedia , lookup
System of polynomial equations wikipedia , lookup
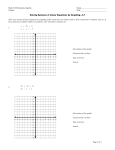
Math 251: Beginning Algebra Section 4.1 Notes Solving Systems of Linear Equations by Graphing Recall, an equation in two variables is linear provided it can be written in the form: Ax + By = C A system of linear equations is a grouping of two or more linear equations. Definition: Examples: (a) (b) A solution of a system of linear equations is an ordered pair that makes both equations true at the same time. A solution of an equation is said to satisfy the equation. Example 1: Decide whether the ordered pair (4,−1) is a solution of each system. (a) (b) 5 x + 6 y = 14 2x + 5 y = 3 − x − y = −3 x + y = −3 Math 251: Beginning Algebra Section 4.1 Notes A system of two equations containing two variables represents a pair of lines. The points of intersection are the solutions of the system. Hence, we can look at their graphs to solve the system! Their graphs can appear in one of 3 ways: Intersect at exactly one point Parallel They are the same line One solution No solution Infinite number of solutions Example 2: Solve the system by graphing. 2x − y = 4 4x + y = 2 Math 251: Beginning Algebra Section 4.1 Notes Example 3: Solve the system by graphing. x + 2y = 4 2 x + 4 y = 12 Example 4: Solve the system by graphing. 2x − y = 4 4x = 2 y + 8