Download Math 101 - Review for Quiz 3 Populations Demographics and the

Math 101 - Review for Quiz 3
Populations
Demographics and the demographic equation
Birth and death rate, growth rate/natural rate of increase, life expectancy, population momentum
Population density
Population pyramids
Survival Rate
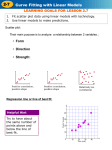
Scatter Plots
Scatter plots, characteristics of scatter plots
Correlation, correlation coefficient, correlation table
Correlation does not imply causation
Probability
Experiment, outcome, sample space, event
Experimental (relative frequency) and theoretical probability, probability distribution
Union (E or F) and intersection (E and F) of events
Complement of an event, P(E’) = 1 - P(E)
Mutually exclusive events, addition principle P(E or F) = P(E)+P(F)
Independence and the multiplication principle (experiment 1 has m outcomes and experiment 2 has n
outcomes, then experiment 1 followed by experiment 2 has m x n outcomes)
The probabilities are multiplied.
Tree diagrams and conditional probability
Probabilities of dependent events, P(E or F) = P(E) + P(F) - P(E and F)
Expected value
Gambler’s Fallacy
1. An experiment consists of selecting a number at random out of the set of numbers {1, 2, 3, 4, 5, 6,
7, 8, 9}. Find the probability that the number is
(a) less than 4.
(b) odd.
(c) less than 4 or odd.
2. Three horses, A, B, and C, are going to race. The probability that A wins is 13 and the probability
that B wins is 21 . What is the probability that C will win? Draw the probability distribution.
3. A couple decides to have four children. What is the probability that they will have more girls than
boys? What is the probability that they will have more boys?
4. The probability that a prize appears in a cookie package is 0.01. What is the probability that 2
packages will contain at least 1 prize?
5. The proportion of individuals in a certain city earning more than $40,000 per year is .25. The
proportion of individuals earning more that $40,000 and having a college degree is .10. Suppose
that a person is randomly chosen and he turns out to be earning more than $40,000, what is the
probability that he is a college graduate?
6. In a certain agricultural region, the probability of a drought during growing season in 0.2, the
probability of a cold spell is 0.15, and the probability of both is 0.1. Find the probability of
(a) not having a drought
(b) either a drought or a cold spell
7. An insurance company sells an insurance policy that pays out $100,000 in the event of job loss due
to illness. The claim rate is 1 in 500 customers. If the policy sells for $250 per person, what is the
expected value for the insurance company (assuming that the number of policies sold is a very large
number)?