Download 1 Lesson 14 (1) Ammeter and Voltmeter Measurement of currents

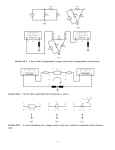
Lesson 14 (1) Ammeter and Voltmeter
Measurement of currents and voltages are made with ammeters and voltmeters. At the
heart of both is a galvanometer, which consists of a coil
in
a magnetic field that deflects when a current passes
through. To measure the current through a resistor R ,
the ammeter should be connected in series as shown:
It is important that the introduction of the ammeter does not change much the original current and voltage across the resistor. Since from the point of view of the external circuit (the rest of the circuit other than the ammeter and the resistor), the resistor is replaced by the ammeter and the resistor in series, the equivalent resistance is R + RA where R A is the resistance of the ammeter. We therefore require R A to be much less than R . This can be accomplished by connecting the galvanometer in parallel with a resistor R A much less than that of the galvanometer. To measure the voltage across the resistor, the voltmeter should be connected in parallel with the resistor as show: The equivalent resistance faced by the external circuit is given by
1
1
1
= +
Req R RV
where RV is the resistance of the voltmeter. In order for Req to be close to R , we now require RV to be much large than R . This can be accomplished by connecting the galvanometer in series with a resistor RV much greater than that of the galvanometer. 1 (2) Circuit Breakers and Fuses A parallel connection of resistors has the advantage over a series connection in that should one resistor burns out and no longer lets through current, there would still be currents going through the remaining good ones. Therefore in the design of the electrical circuits that supply power for household use, electrical outlets are grouped together and connected to a pair of 120V power lines as shown: The drawback of such a connection is that as more appliances are connected, the less is the equivalent resistance offered to the power supply, and the more is the current drawn. As a result, more power is dissipated as heat in the connecting wires 2
( P = I rms
R ). When the power is excessive, it becomes a fire hazard. To limit the current drawn, a circuit breaker or fuse can be connected as shown. It would break the circuit when the current exceeds a specified amount. Example: Two 150W light bulbs and a 200W toaster are plugged into electrical outlets that draw power from the same pair of 120V power lines. A 800W hair dryer is now also plugged in. If the circuit breaker is designed to trip at 10A, will the circuit trip? Solution: At the point of tripping, the power drawn from the power lines is P = I rmsVrms = 10 × 120 = 1200W The total power consumed when all four are plugged in is Ptotal = 2 × 150 + 200 + 800 = 1300W The current drawn from the main would exceed 10A to supply this power. Hence the breaker will trip. 2 (3) Kirchhoff’s Rules In general, an electric circuit cannot be decomposed into series and parallel combinations of resistors. But the currents and voltages in the circuit can always be found using the Kirchhoff rules. A circuit always has junctions and loops. A junction is a point where more than two branches (paths) meet. Drawing arrows to represent currents going in and out of a junction, the junction rule states that the sum of currents going in is equal to the sum of currents going out: ! I =! I in
out
This is because the junction is considered to be so small that it cannot accumulate electric charge. For any loop in the circuit, a sense of traverse is first introduced. The loop rule states that the sum of increments of potentials across each resistor and each source of emf in the loop is zero: " !V = 0 loop
We have seen that this is simply because each point of the circuit has a definite potential. The increments of potentials for resistors and ideal emf sources are as shown: The procedure to solve for the currents in any circuit is as follows: 1. Assign current variables: Choose any branch to start with, assign an arrow and label it with the current variable I1 . At each junction, assign as few new current variables as needed, consistent with the junction rule. An example as shown: 2. Apply loop rules: Select as many loops as there are current variables. (The loops should lead to independent equations.) For each loop, choose a direction of traverse and write down the loop rule, using for !V the appropriate expressions for resistors and sources of emf. 3 3. Solve the system of simultaneous linear equations for the current variables. A negative value for a current means that it is in the opposite direction to the current flow arrow . Example: In the following circuit, the batteries are all ideal. Find (1) the currents in each resistor, (2) the power delivered or absorbed by each battery, and (3) the potential difference Vb !Va between the points a and b in the circuit. Solution: The currents variables are assigned and two loops both traversed clockwise are chosen as shown Application of loop rules: Bottom loop : 14 ! 4I1 ! 9 ! 3I 2 = 0 !2 ( I1 ! I 2 ) + 3I 2 + 9 = 0 Top loop: Simplifying and putting in standard form, the pair of equations become 4I1 + 3I 2 = 5 2I1 ! 5I 2 = 9 Subtracting two times the second equation from the first: 4 13I 2 = !13
I 2 = !1 Substitute into the second equation: The currents are indicated in the diagram below: I1 =
9 + 5I 2
= 2 2
The power delivered by the batteries are: P14 = 2 !14 = 28W
P9 = 1! 9 = 9W Calculating the increment of potential along the path from a to b by way of the 14V battery and 4! resistor: Vb !Va = 14 ! 2 " 4 = 6V We get a third loop equation from the outermost loop: 14 ! 4I1 ! 2 ( I1 ! I 2 ) = 0 This is just the sum of the equations for the top and bottom loops, and so does not yield additional information. 5 Example: An example of a problem with three independent loops is as shown: This is called the Wheatstone bridge. If the resistor R5 is removed, the resistor series combination R1 + R2 is in parallel with the series combination R3 + R4 , and the same potential difference ℰ exists across both combinations. Within each series combination, this potential difference is divided up in proportion to the resistances in the combination. Therefore, if R1 R3
=
R2 R4
the potentials at the two points where the bridge R5 were connected to are equal. If R5 is now reconnected, no current will flow through is. This observation forms the basis for the measurement of resistance. Suppose R1 is the unknown resistance, while R2 , R3, R4 are all known and variable, and R5 is replaced by a galvanometer. By varying R3 and R4 , the reading on the galvanometer is made to read zero. Then R1
can be calculated from the above relation. In general, for any given values of the resistances, the currents can be determined with the assignment shown, and using the three loop equations as follows: Left loop: !R1I 2 ! R5 I 3 + R3 ( I1 ! I 2 ) = 0 Right loop: R5 I 3 ! R2 ( I 2 ! I 3 ) + R4 ( I1 ! I 2 + I 3 ) = 0 Big loop: E ! R1I 2 ! R2 ( I 2 ! I 3 ) = 0 which form a system of three equations for three unknowns. Left loop: !R1I 2 ! R5 I 3 + R3 ( I1 ! I 2 ) = 0 6