Download - Catalyst

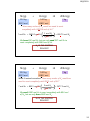
10/9/2011
Chapter 3
•
•
•
•
•
•
•
•
•
Atomic Masses(3.1)
The Mole (3.2)
Molar Mass (3.3)
Percent Composition (3.4)
Determining the Formula of a Compound (3.5)
Chemical Equations (3.6)
Balancing Chemical Equations (3.7)
Introducing Stoichiometry (3.8)
Introducing Limiting Reagents (3.9)
This is the outline for the content we will cover in
lecture. Please read the entire chapter.
A Brief History of the amu
• Stanislao Canizzaro (1826-1910) proposed that the H atom
be used as a standard of mass and set its atomic mass at 2.
• Other chemists of the day wanted to use a more massive
atom to reduce experimental error.
• Chemists eventually took the mass of naturally occurring
oxygen (O) to be 16 amu.
• Concurrently, physicists defined the oxygen-16 isotope as
16 amu.
Are these two definitions that use oxygen the same?
NO. Naturally occurring oxygen is a combination of three stable
isotopes, oxygen-16, oxygen-17, and oxygen-18.
These two definitions resulted in conflicting values.
• Finally in the 1950s the carbon-12 isotope was adapted as
the standard…hence 1 amu = 1/12 the mass of one 12C atom.
2
1
10/9/2011
Some Isotope Comparisons
Element
Isotope
Hydrogen
1H
2H
Carbon
12C
13C
Sulfur
32S
33S
34S
36S
Lithium
6Li
7Li
Average
Atomic Mass
(amu)
Mass of
Isotope (amu)
Relative
Abundance
1.00782
2.01410
99.9844%
0.0156%
1.0079
12 (exact)
13.00335
98.892%
1.108%
12.01115
31.972071
32.971458
33.967867
35.967080
95.06%
0.74%
32.064
4.18%
0.0136%
6.015123
7.016005
7.5%
92.5%
6.941
3
Calculating Atomic Mass
Let’s say we have a sample of 1000 carbon (C) atoms. Based on
isotopic abundance:
989 weigh 12 amu (98.9%)
11 weigh 13 amu (1.1%)
What is the average mass of a carbon atom in this sample?
Atomic mass =
=
(989 C atoms)*(12 amu) + (11 C atoms)*(13 amu)
1000 C atoms
(989 C atoms)*(12 amu) + (11 C atoms)*(13 amu)
1000 C atoms
1000 C atoms
=
(989/1000)*(12 amu) + (11/1000)*(13 amu)
=
(0.989)*(12 amu) + (0.011)*(13 amu)
=
12.011 amu
2
10/9/2011
Calculating Atomic Mass
Let’s say we have a sample of 1000 lithium (Li) atoms. Based on
isotopic abundance:
925 weigh 7 amu (92.5%)
75 weigh 6 amu (7.5%)
What is the average mass of a lithium atom in this sample?
Atomic mass
=
(0.925)*(7 amu) + (0.075)*(6 amu)
=
6.9 amu
5
Don’t confuse “Atomic Mass” with the
mass of one atom!!
• An atom can be only one isotope at a time.
12C:
13C:
Z = 12, isotopic mass = 12 amu (exactly)
Z = 13, isotopic mass = 13.003354 amu
• The Atomic Mass (aka Atomic Weight or Average
Atomic Mass) is the average of the atomic masses of
all of the element's isotopes, weighted by isotopic
abundance.
• Naturally occurring carbon has an atomic mass of
12.011 amu
• There is no carbon isotope that weighs 12.011 amu.
6
3
10/9/2011
Determining isotopic mass using a
Mass Spectrometer
• Stream of vaporized atoms is bombarded with highspeed electrons, which knock electrons off the gaseous
atoms, turning them into cations.
• Gaseous cations are accelerated through magnetic field,
and their paths are bent according to their mass.
7
Counting by Weighing
• Chemical reactions occur at the microscopic level,
between individual molecules and/or atoms.
• In the lab, we measure substances in terms of grams or
milliliters…these are macroscopic measurements.
• The number of molecules in 1 g of water will be different
than the number of molecules in 1 g of glucose, because
these molecules have different masses.
• We need a way to convert between the microscopic and
macroscopic descriptions.
4
10/9/2011
Dozen – mass
12 red marbles (7g each) = 84g
12 yellow marbles (4g each) = 48g
Mole – mass
6.022 x 1023 atoms Fe = 55.85g Fe
6.022 x 1023 atoms S = 32.07g S
How many 12C atoms in 12 g?
Mass of one carbon-12 atom: 1.992646632 x 10-23 g
Divide 12 g (exact) by the mass of a single 12C atom:
12 g of carbon-12
1.992646632 x
10-23
g/
C atom
= 6.022 141 511 x 1023 C atoms
Avogadro’s Number (NA)
One mole (mol) of a substance contains Avogadro’s Number
of elementary entities.
Note: the elementary entities may be atoms, molecules, ions,
electrons, other particles, or specified groups of such
particles.
11
5
10/9/2011
Interpreting the Mole
If we had 1 mol of bicycles…
– How many mol bike seats would we
1 mol seats
have?
2 mol tires
– Tires?
– Spokes? (assuming 36
spokes/wheel) 72 mol spokes
If we had 1 mol of isopropyl alcohol (C3H8O)…
CH3
C
H
CH3
HO
– How many mol O atoms would we
have?
1 mol O atoms
– Carbon atoms? 3 mol C atoms
– Hydrogen atoms? 8 mol H atoms
12
What does one mole look like?
For condensed-phase
substances (solids and
liquids), one mole is a
convenient “hand-full” sized
quantity.
1 mol N2(g),
V = 22.4 L
For gas-phase substances
at room temperature at sea
level, one mole has a
volume of about 22.4 L.
1 mol H2O(l)
1 mol NaCl(s)
13
6
10/9/2011
Molar Mass
How much does one mole of a substance weigh?
Find the molar mass of carbon dioxide, CO2:
1 amu = 1.661 x 10–24 g (1/12 the mass of one 12C atom)
12.011 amu/C + 2 15.999 amu/O = 44.009 amu/CO2
? g/mol = 44.009 amu
molecule CO2
23
1.661 x 10-24 g 6.022 x 10 molecules CO2
1 mol CO2
1 amu
= 44.009 g/mol
The mole and the amu are defined in
such a manner that the atomic weights
given in the periodic table can be
interpreted as molar masses.
12.011 g/mol C
+ 2 15.999 g/mol O
44.009 g/mol CO2
Molar Mass as a Conversion Factor
Molar mass (the mass of one mole of a substance), allows
us to convert between macroscopic and particulate points
of view.
How many grams of oxygen corresponds to 0.50 moles?
? g O2 = 0.5 mol O2
32 g O2
1 mol O2
= 16 g O2
How many moles of oxygen are there in 1.2 grams?
? mol O2 = 1.2 g O2
1 mol O2
32 g O2
= 0.038 mol O2
15
7
10/9/2011
Calculating the Moles in a Given
Mass of a Compound
Problem: Sodium phosphate is a component of some detergents.
How many moles are in a 38.6 g sample?
Plan:
Determine the formula and then the molar mass from
the masses of each element, multiplied by the subscripts.
Solution: The formula is Na3PO4.
Calculating the molar mass:
MM = 3 x sodium + 1 x phosphorous + 4 x oxygen
= (3 x 22.99 g/mol) + (1 x 30.97 g/mol) + (4 x 16.00 g/mol)
= 68.97 g/mol + 30.97 g/mol + 64.00 g/mol = 163.94 g/mol
Converting mass to moles:
moles Na3PO4 = 38.6 g Na3PO4 x
1 mol Na3PO4
163.94 g Na3PO4
= 0.235 mol Na3PO4
Aluminum (Al)
atomic weight = 26.98 amu.
molar mass = 26.98 g/mol
1 mol Al contains 6.022 x 1023 Al atoms
Lead (Pb)
atomic weight = 207.2 amu.
molar mass = 207.2 g/mol
1 mol Pb contains 6.022 x 1023 Pb atoms
17
8
10/9/2011
Table salt (NaCl)
formula mass = 58.44 amu
molar mass = 58.44 g/mol
1 mol of table salt contains 6.022 x 1023
NaCl formula units…this means:
6.022 x 1023 sodium ions (Na+)
and…
6.022 x 1023 chloride ions (Cl-)
18
water
O
H
H
1 mol sucrose
contains 6.022 x 1023
sucrose molecules.
1 mol water contains
6.022 x 1023 water
molecules.
HO
HO
CH
H2 C
H2O
Molc.Wt.: 18.02 amu
MM: 18.02 g/mol
sucrose (table sugar) O
H2
C
HO
isopropyl alcohol
CH3
C
H
CH3
HO
C3H8O
Molc.Wt.: 60.10 amu
MM: 60.10 g/mol
HO
CH2
O
OH
CH
CH
1 mol isopropyl
alcohol contains
6.022 x 1023
isopropyl alcohol
molecules.
C
O
CH
OH
CH
CH
CH
CH
OH
C12H22O11
OH Molc.Wt.: 342.3 amu
MM: 342.3 g/mol
19
9
10/9/2011
More Practice…
You have 3.0 mol of aluminum sulfate. Calculate the
following quantities:
1. The total number of Al atoms.
2. The total number of Al2(SO4)3 formula units.
3. The moles of sulfate ions.
4. The moles of oxygen atoms.
More Practice…
How many mol of ions are present in a 1.0-g sample of zinc
oxide (ZnO)?
Calculate the mass of 4.85 mol of acetic acid, CH3COOH.
21
10
10/9/2011
Atoms
Chemical
Formula
Molecules/
Formula Units
6.022 x 1023
mol
6.022 x 1023
mol
Moles
11
10/9/2011
Mass Fraction and Mass %
Mass of Red Balls = 3 balls x 3.0 g/ball = 9.0 g
Mass Fraction Red = 9.0 g / 16.0 g total = 0.56
Mass % Red = 0.56 x 100 = 56% red
Mass Fraction Purple
and Mass
= % Purple =
2 balls x 2.0 g/ball / 16.0 g total = 0.25 = 25%
Similarly, mass fraction yellow = 3 x 1.0 /16.0 = 0.19
Check: 56% + 25% + 19% = 100%
Calculate the Percent Composition of
Sulfuric Acid H2SO4
Molar mass of sulfuric acid =
2(1.008 g/mol) + 1(32.07 g/mol) + 4(16.00 g/mol) = 98.09 g/mol
%H = 2(1.008 g H) x 100 = 2.055% H
98.09 g
%S = 1(32.07 g S) x 100 = 32.69% S
98.09 g
%O =
4(16.00 g O)
x 100 = 65.25% O
98.09 g
Check = 100.00%
12
10/9/2011
Calculating Mass Percentage and Masses of
Elements in a Sample of a Compound
Problem: Sucrose (C12H22O11) is common table sugar.
(a) What is the mass percent of each element in sucrose?
(b) How many grams of carbon are in 24.35 g of sucrose?
(a) Determining the mass percent of each element:
mass of C per mole sucrose = 12 x 12.01 g C/mol = 144.12 g C/mol
mass of H / mol =
22 x 1.008 g H/mol = 22.176 g H/mol
mass of O / mol =
11 x 16.00 g O/mol = 176.00 g O/mol
total mass per mole = 342.296 g/mol
Finding the mass fraction of C in sucrose & % C :
Mass fraction of C = mass of C per mol sucrose = 144.12 g C/mol
mass of 1 mol sucrose
342.30 g sucrose/mol
= 0.42103
To find mass % of C = 0.4210 x 100 =
42.103%
Calculating Mass Percents and Masses of
Elements in a Sample of Compound - II
(a) continued
Mass % of H =
mol H x M of H x 100
mass of 1 mol sucrose
= 22 x 1.008 g H x 100
342.30 g
= 6.479% H
Mass % of O =
mol O x M of O
x 100
mass of 1 mol sucrose
= 11 x 16.00 g O x 100
342.30 g
= 51.42% O
(b) Determining the mass of carbon in 24.35 g sucrose:
Mass (g) of C = mass of sucrose x ( mass fraction of C in sucrose)
Mass (g) of C = 24.35 g sucrose x
0.4210 g C
1 g sucrose
= 10.25 g C
13
10/9/2011
Empirical and Molecular Formulas
Empirical Formula - The simplest formula for a compound that
agrees with the elemental analysis! The smallest set of whole
numbers of atoms.
Molecular Formula - The formula of the compound as it really
exists. It must be a multiple of the empirical formula.
14
10/9/2011
Elemental Analysis
Decomposition or combustion analysis is used to determine
the mass of each type of element present in a compound.
Figure 3.5:
Schematic Diagram of a Combustion Analysis Device
Determining Empirical Formulas from
Measured Masses of Elements - I
The elemental analysis of a sample gave the following results:
5.677g Na, 6.420 g Cr, and 7.902 g O. What is the empirical
formula and name of the compound?
Start by finding the moles of each element:
1 mol Na
= 0.2469 mol Na
22.99 g Na
Moles of Cr = 6.420 g Cr x 1 mol Cr = 0.1235 mol Cr
52.00 g Cr
Moles of O = 7.902 g O x 1 mol O = 0.4939 mol O
16.00 g O
Moles of Na = 5.677 g Na x
15
10/9/2011
Determining Empirical Formulas from
Masses of Elements - II
Constructing the preliminary formula:
Na0.2469 Cr0.1235 O0.4939
Converting to integer subscripts:
(dividing all by smallest subscript)
Na1.999 Cr1.000 O3.999
Rounding off to whole numbers:
Na2CrO4
sodium chromate
Determining the Molecular Formula from
Elemental Composition and Molar Mass - I
The sugar burned for energy in cells of the body is glucose (MM =
180.16 g/mol), elemental analysis shows that it contains
40.00 mass % C, 6.729 mass % H, and 53.27 mass % O.
(a) Determine the empirical formula of glucose.
(b) Determine the molecular formula of glucose.
HINT: We are only given mass % so we will assume a 100 g sample.
Solution:
Mass carbon = 40.00% x 100 g/100% = 40.00 g C
Mass hydrogen = 6.729% x 100 g/100 = 6.729 g H
Mass oxygen = 53.27% x 100 g/100 = 53.27 g O
99.999 g cmpd
16
10/9/2011
Determining the Molecular Formula from
Elemental Composition and Molar Mass - II
Converting from grams of elements to moles:
Moles of C = 40.00 g C x
Moles of H = 6.719 g H x
Moles of O = 53.27 g O x
1 mole C
= 3.331 moles C
12.01 g C
1 mol H
= 6.666 moles H
1.008 g H
1 mol O = 3.330 moles O
16.00 g O
Constructing the preliminary formula C 3.33 H 6.67 O 3.33
Converting to integer subscripts, ÷ all subscripts by the smallest #:
C 3.33/3.33 H 6.667 / 3.33 O3.33 / 3.33 = C1H2O1 = CH2O
Empirical Formula!!
Determining the Molecular Formula from
Elemental Composition and Molar Mass - III
(b) Determining the molecular formula:
The molar mass of the empirical formula is:
(1*C) + (2*H) + (1*O) = (1*12.01) + (2*1.008) + (1*16.00)
= 30.03 g/mol
whole-number multiple = MM of the compound
empirical molar mass
Stated in the
problem
180.16 g/mol
= 6.00 = 6
30.03 g/emp. mol
Therefore the molecular formula is:
C1x6H2x6O1x6 =
C6H12O6
17
10/9/2011
Ascorbic acid (Vitamin C ) - I
(contains only C , H , and O)
Upon combustion in excess oxygen, a 6.49 mg sample yielded
9.74 mg CO2 and 2.64 mg H2O.
Calculate the empirical formula of ascorbic acid.
Mass of C and H in the CO2 and H2O, respectively:
9.74 x10-3g CO2
X
12.01 g C =
44.01 g CO2
2.65 x 10-3 g C
2.64 x10-3g H2O X
2.016 g H =
18.02 g H2O
2.95 x 10-4 g H
Mass of O (by difference!!):
6.49 x10-3 g sample - 2.65 x10-3 g C - 2.95 x10-4g H =
3.55 x 10-3 g O
Vitamin C combustion - II
Now we convert to moles:
-3
C: 2.65 x 10 g C X 1 mol C
12.011g C
H: 2.95 x 10-3 g H X 1 mol H
1.008g H
-3
O: 3.55 x 10 g O X
1 mol O
16.00g O
-4
= 2.21 x 10 mol C
= 2.93 x 10-4 mol H
-4
= 2.22 x 10 mol O
Divide each by smallest (2.21 x 10-4 ):
C = 1.00
Multiply each by 3:
H = 1.33
(to get ~integers)
O = 1.00
C3H4O3
C = 3.00 = 3.0
H = 3.99 = 4.0
O = 3.00 = 3.0
18
10/9/2011
If the empirical formula of ascorbic acid is C3H4O3, and
the molecular mass of ascorbic acid is
176 g/mol, what is the molecular formula?
C3H4O3: (3* ~12) + (4*~1) + (3*~16) =
1.
2.
3.
4.
5.
C3H4O3
C6H8O6
C9H12O9
C12H16O12
None of the above
Chemical Equations
• Chemistry is the study of the rearrangement of matter due
to the flow of energy.
• In a chemical reaction, some bonds are broken and others
are formed, resulting in a reorganization of the atoms.
• Atoms are neither created or destroyed in a chemical
reaction!
When methane (CH4) reacts with oxygen,
carbon dioxide and water are formed…
+
+
Reactants and products must occur in numbers that give the
same number of each type of atom on both sides of the
arrow.
39
19
10/9/2011
Formulas of Elements and
Compounds
•
The name or chemical formula of a compound
gives you information about the relative number
of atoms in the compound
– sodium chloride: NaCl
– copper(II) nitrate: Cu(NO3)2
– carbon tetrachloride: CCl4
•
The formula of most elements (particularly metals)
is simply the element symbol
– tungsten: W
– calcium: Ca
– boron: B
– carbon (graphite): C
•
A solution of C60
Allotropes of
sulfur
Elemental forms of nonmetals are often found as
molecules
– H2, N2, O2, F2, Cl2, Br2, I2
– S8, C60, P4
Interpreting Chemical Equations
• A reaction results in the rearrangement of atoms in one
or more reactants to produce one or more products.
• What is this chemical equation telling us?
CO(g)
+
2H2(g)

CH3OH(l)
1 CO
molecule
+
2 H2 molecules

1 CH3OH molecule
6.022 x 1023
CO molecules
+
2(6.022 x 1023)
H2 molecules

6.022 x 1023 CH3OH
molecules
1 mol CO
molecules
+
2 mol H2
molecules

1 mol CH3OH
molecules
1 g CO
molecules
+
2 g H2
molecules

1 g CH3OH
molecules
20
10/9/2011
Balancing Chemical Equations
1. Determine what reaction is
occurring. What are the reactants,
products, and physical states
involved?
2. Write the unbalanced equation
that summarizes the reaction in
step 1.
3. Balance the equation by
inspection. Do not change the
identities (formulas) of any of the
reactants or products.
(dissolved in water)
At temperatures near room temperature, most
elements are in the solid phase. Exceptions:
• Gases: H2, N2, O2, F2, Cl2, He, Ne, Ar, Kr, Xe
• Liquids: Hg, Br2
43
How to Balance Equations
Mass Balance (or Atom Balance)- same number of each element
on each side of the equation:
(1) start with largest/most complicated molecule
(2) progress to other elements, leaving lone elements for last
(3) make all whole numbers
(4) re-check atom balance
1 CH4 (g) +
O2 (g)
1 CO2 (g) +
H2O (g)
1 CH4 (g) +
O2 (g)
1 CO2 (g) + 2 H2O (g)
1 CH4 (g) + 2 O2 (g)
1 CO2 (g) + 2 H2O (g)
1 CH4 (g) + 2 O2 (g)
1 CO2 (g) + 2 H2O (g)
21
10/9/2011
Balancing Chemical Equations - I
Problem: The hydrocarbon hexane is a component of gasoline that
burns in an automobile engine to produce carbon dioxide and
water, as well as energy. Write the balanced chemical equation for
the combustion of hexane (C6H14).
Plan: Write the skeleton equation, converting the words into
compounds, with blanks before each compound. Begin element
balance, putting 1 on the most complex compound first, and save
oxygen until last!
C6H14 (l) +
O2 (g)
CO2 (g) +
H2O(g) + Energy
Begin with one C6H14 molecule which means that we will form 6 CO2!
1 CH
6 14 (l) +
O2 (g)
6 CO
2 (g)
+
H2O(g) + Energy
Balancing Chemical Equations - II
The H atoms in the hexane will end up as H2O, and we have 14
H atoms. Since each water molecule has two H atoms, we will get
a total of 7 water molecules.
1 CH
6 14 (l) +
O2 (g)
6 CO
2 (g) +
7 H O + Energy
2 (g)
Since oxygen atoms only come as diatomic molecules (two O atoms,
O2),we must have even numbers of oxygen atoms on the product side.
We do not since we have 7 water molecules! Therefore, multiply
everything by 2, giving a total of 2 hexane molecules, 12 CO2
molecules, and 14 H2O molecules.
2 CH
6 14 (l) +
O2 (g)
12 CO
2 (g)
+ 14 H2O(g) + Energy
This now gives 24 O from the carbon dioxide, and 14 O atoms from the
water, which will be a total of 24+14 = 38 O or 19 O2 !
2 CH
19 O
6 14 (l) +
2 (g)
12 CO
14 H O + Energy
2 (g) +
2 (g)
22
10/9/2011
Balancing Practice
a) NH3(g) + HCl(g)  NH4Cl(s)
b) NO(g) + H2(g)  N2(g) + H2O(l)
c) Fe2O3(s) + HNO3(aq)  Fe(NO3)3(aq) + H2O(l)
d) Dihydrogen sulfide gas reacts with aqueous lead(II) nitrate to form
solid lead (II) sulfide and aqueous nitric acid.
e) Solid ammonium nitrite decomposes to nitrogen gas and gaseous
water.
f) Solid antimony trichloride is formed from its elements at room
temperature.
Stoichiometry: A Recipe for Chemistry
• A recipe specifies that the following ingredients…
– 1 ¾ cup cake flour
– 3 tsp baking powder
– 2 oz. baking chocolate
– 1 ½ cup sugar
- ½ cup butter
- 4 eggs
- ½ cup milk
…are necessary to bake one chocolate cake.
• Similarly, chemical reactions include information about how
much of each reactant you need to produce a certain amount
of product.
CH4 + 2 O2  CO2 + 2 H2O
• Chemistry occurs on the atomic/molecular level, but it is
extremely difficult to keep track of one atom or molecule at a
time.
• We use molar ratios to relate the mass of a sample (a
macroscopic measurement) to the number of atoms or molecules
in a sample (a microscopic measurement).
23
10/9/2011
Mole Ratios
• We can use a balanced chemical equation to predict the
number of moles of products that a given number of
moles of reactants will produce.
2H2O(l) 
2H2O(l)
2H2(g) + O2(g)
2H2(g) + O2(g)
4H2O(l)
4H2(g) + 2O2(g)
Mole Ratios (cont)
• What if we wanted to know the number of moles of H2 and O2
produced from the decomposition of 5.8 mol of H2O?
2H2O(l)  2H2(g) + O2(g)
• We know the following:
2 mol H2O
2 mol H2
2 mol H2O
1 mol O2
• We can represent these molar equivalencies as conversion
factors:
2 mol H2O
~
2 mol H2
2 mol H2
2 mol H2O
2 mol H2O
~
1 mol O2
=
1 mol H2
1 mol H2O
1 mol O2
2 mol H2O
24
10/9/2011
Mole Ratios (cont)
• Now we can answer the question…How many moles of H2
and O2 are produced from the decomposition of 5.8 mol of
H2O?
2H2O(l)  2H2(g) + O2(g)
? mol H2
= 5.8 mol H2O
1 mol H2
=
5.8 mol H2
=
2.9 mol O2
1 mol H2O
? mol O2
= 5.8 mol H2O
1 mol O2
2 mol H2O
Stoichiometry and Mass
Consider the reaction in which powdered aluminum and
finely ground iodine react violently to produce aluminum
iodide:
2 Al(s) + 3 I2(s)  2 AlI3(s)
Let’s say we have 35.0 g of aluminum powder.
How many grams of ground iodine do we need to react
completely with this amount of aluminum?
25
10/9/2011
Stoichiometry and Mass (cont)
We need to construct the mole ratios from our balanced
chemical equation.
2 Al(s) + 3 I2(s)  2 AlI3(s)
2 mol Al
~
3 mol I2
3 mol I2
2 mol Al
How many grams of I2 are required to react with 35.0 g Al?
? g I2 = 35.0 g Al
1 mol Al
3 mol I2
253.8 g I2
26.98 g Al
2 mol Al
1 mol I2
= 493.87 g I2
=
494 g I2
Calculating the Amounts of Reactants and
Products in a Reaction Sequence - I
Calcium phosphate could be prepared from phosphorus in the following
reaction sequence:
POW!!
3 P4 (s) + 10 KClO3 (s)
3 P4O10 (s) + 10 KCl (s)
P4O10 (s) + 6 H2O (l)
2 H3PO4 (aq) + 3 Ca(OH)2 (aq)
4 H3PO4 (aq)
6 H2O(aq) + Ca3(PO4)2 (s)
Given 15.50 g P4 and sufficient KClO3 , H2O and Ca(OH)2. What mass
of calcium phosphate could be formed?
Plan:
(1) Calculate moles of P4 provided.
(2) Use molar ratios to get moles from P4 to Ca3(PO4)2.
(3) Convert the moles of product into mass using the
molar mass of calcium phosphate.
26
10/9/2011
Calculating the Amounts of Reactants and
Products in a Reaction Sequence - II
moles of phosphorous = 15.50 g P4 x
For Reaction #1: 3 P4 (s) + 10 KClO3 (s)
1 mole P4
= 0.1251 mol P4
123.88 g P4
3 P4O10 (s) + 10 KCl (s)
For Reaction #2: 1 P4O10 (s) + 6 H2O (l)
For Reaction #3: 2 H3PO4 + 3 Ca(OH)2
4 H3PO4 (aq)
1 Ca3(PO4)2 + 6 H2O
0.1251 moles P4 x 3 moles P4O10 x 4 moles H3PO4 xx 1 mole Ca3(PO4)2
3 moles P4
1 mole P4O10
2 moles H3PO4
= 0.2502 moles Ca3(PO4)2
Molar mass of Ca3(PO4)2 = 310.18 g/mol
mass of product = 0.2502 moles Ca3(PO4)2 x
= 77.61 g Ca3(PO4)2
Demo:
310.18 g Ca3(PO4)2
1 mole Ca3(PO4)2
3 P4(s) + 10 KClO3(s)  3 P4O10(s) + 10 KCl(s)
Heat of reaction = - 9,425 kJ
The head of safety matches are made of an oxidizing agent such as
potassium chlorate, mixed with sulfur, fillers and glass powder. The side of
the box contains red phosphorus, binder and powdered glass. The heat
generated by friction when the match is struck causes a minute amount of
red phosphorus to be converted to white phosphorus, which ignites
spontaneously in air. This sets off the decomposition of potassium
chlorate to give oxygen and potassium chloride. The sulfur catches fire
and ignites the wood.
The head of "strike anywhere" matches contain an oxidizing agent
such as potassium chlorate together with tetraphosphorus trisulfide (P4S3),
glass and binder. The phosphorus sulfide is easily ignited, the potassium
chlorate decomposes to give oxygen, which in turn causes the phosphorus
sulfide to burn more vigorously.
27
10/9/2011
Limiting Reactants
Given a balanced chemical equation, the amount of
reactants available to react determines the amount of
products we can produce.
1 ¾ cup cake flour
3 tsp baking powder
2 oz. baking chocolate
1 ½ cup sugar
½ cup butter
4 eggs
½ cup milk
1 ¾ cup cake flour
3 tsp baking powder
2 oz. baking chocolate
1 ½ cup sugar
½ cup butter
one whole chocolate cake
Having only 2 eggs available limits the
amount of cake we can make, even though
we have plenty of the other ingredients.
one half of a chocolate cake
2 eggs
½ cup milk
The same kind of thing happens
in chemical reactions!
Limiting Reagent
3N2 (g) + 9 H2 (g)  6 NH3 (g)
28
10/9/2011
LRs in Action
CO(g)
+
2H2(g)
CH3OH(l)

Initial
1 mol
2 mol
0 mol
Change
- 1 mol
- 2 mol
+ 1 mol
End
0 mol
0 mol
1 mol
Both reactants are completely used
up…neither CO or H2 limit the
production of CH3OH.
LRs in Action (cont)
CO(g)
+
2H2(g)
CH3OH(l)

Initial
0.5 mol
2 mol
0 mol
Change
- 0.5 mol
- 1 mol
+ 0.5 mol
End
0 mol
1 mol
0.5 mol
CO is used up before H2 …
CO limits the production of
CH3OH.
29
10/9/2011
LRs in Action (cont)
CO(g)
+
2H2(g)
CH3OH(l)

Initial
1 mol
1 mol
0 mol
Change
- 0.5 mol
- 1 mol
+ 0.5 mol
End
0.5 mol
0 mol
0.5 mol
H2 is used up before CO…
H2 limits the production of
CH3OH.
Example
• Suppose 25.0 kg of nitrogen gas and 5.00 kg of
hydrogen gas are mixed and reacted to form
ammonia. Calculate the mass of ammonia
produced when this reaction is run to completion.
N2(g)
25.0 kg
+
3 H2(g)
5.00 kg

2 NH3(g)
? kg
30
10/9/2011
Example (cont)
N2(g)
+
3H2(g)
25.0 kg
5.00 kg
MM
MM
mol N2
Use mole
ratios to
determine LR
mol LR
N2(g)
25.0 kg
+

? kg
MM
mol H2
mol NH3
mol LR
3H2(g)
2NH3(g)
mol NH3

2NH3(g)
? kg
5.00 kg
? mol N2 = 25.0 kg N2 1000 g N2
1 kg N2
1 mol N2
28.01 g N2
? mol H2 = 5.00 kg H2 1000 g H2
1 kg H2
1 mol H2
= 2480.16 mol H2
2.016 g H2
= 892.54 mol N2
To determine which of this reactants is limiting, ask the
following question:
“How many moles of N2 would we need to react
completely with 2480.16 mol of H2?”
31
10/9/2011
N2(g)
+
3H2(g)
25.0 kg
5.00 kg
892.5 mol
2480.2 mol

2NH3(g)
? kg
“How many moles of N2 would we need to react
completely with 2480.16 mol of H2?”
? mol N2 = 2480.2 mol H2
1 mol N2
3 mol H2
= 826.73 mol N2
We have 892 mol N2, but we only need 827 mol N2 to
react completely with 2480 mol of H2.
H2 IS THE LIMITING
REAGENT.
N2(g)
+
3H2(g)
25.0 kg
5.00 kg
892.5 mol
2480.2 mol

2NH3(g)
? kg
What if instead we asked: “How many moles of H2 would we
need to react completely with 892.5 mol of N2?”
? mol H2 = 892.5 mol N2
3 mol H2
1 mol N2
= 2677.5 mol H2
We need 2680 mol H2 to react completely with 892 mol
of N2, but we only have 2480 mol H2.
H2 IS THE LIMITING
REAGENT.
32
10/9/2011
N2(g)
+
3H2(g)

25.0 kg
5.00 kg
892.5 mol
2480.2 mol
2NH3(g)
? kg
LIMITING REAGENT
? kg NH3
= 2480.2 mol H2
2 mol NH3
3 mol H2
17.03 g NH3
1 mol NH3
1 kg NH3
1000 g NH3
= 28.1585 kg NH3 = 28.2 kg NH3
Making the LR work for YOU
• Chemistry happens at the particulate level…
…so the limiting reactant in a chemical equation must be
determined by comparing numbers of moles.
• To determine which reactant is the LR, we must compare the
following quantities…
– what we have (based on the problem set up)
– what we need (based on the balanced chemical equation)
• The mole ratios in a chemical equation are crucial for
determining the LR…
• The reactant for which you have fewer moles is not
necessarily the LR!!
33
10/9/2011
Theoretical vs. Actual Yield
• The theoretical yield of a reaction is the amount of
product that would be formed under ideal reaction
conditions in which starting materials are completely
consumed (up to the LR). This is a calculated number.
• The actual yield is the amount of product that is actually
produced in real life (in the lab).
• The actual yield is always less than the theoretical yield
because…
–
–
–
–
LR starting materials may not be completely consumed
side reactions may occur
the reverse reaction may occur
there may be loss of product during purification steps
Percent Yield
A comparison of…
how much product we actually produced
to
how much product we could theoretically produce
Gives us the percent yield of a chemical reaction.
% yield =
actual yield
theoretical yield
100
34
10/9/2011
N2(g)
+
3H2(g)
25.0 kg
5.00 kg
892.5 mol
2480.2 mol
LIMITING REAGENT

2NH3(g)
28.2 kg
Theoretical
Yield
In a certain experiment, the actual yield of this reaction
was only 26.7 kg NH3. What was the percent yield?
% yield =
26.7 kg NH3
28.2 kg NH3
100
= 94.68% = 94.7%
Percent yield should never be greater than 100%. If it is, there is
something wrong with your theoretical yield calculation, or with
the actual yield you obtained experimentally.
If two compounds are about to react, which statement about the
reaction states an accurate observation?
1. If temperature conditions can be kept optimal, both
compounds will fully react with no excess.
2. The reactant present with the fewest grams will be the limiting
reactant.
3. The reactant present with the fewest moles will be the limiting
reactant.
4. None of the statements are accurate.
A limiting reactant can be determined only when both
the moles of the two compounds AND the mole ratio
by which the compounds react are known.
35
10/9/2011
Tips for Stoichiometric Success
•
Make sure your chemical equation is balanced.
•
Always compare moles, not mass.
•
Use mole ratios from your balanced chemical equation to
determine the limiting reactant.
•
Remember…
– theoretical yield is a calculated quantity.
– actual yield is a measured quantity.
•
If your percent yield is greater than 100%...
– something is wrong with the theoretical yield you
calculated, or…
– something is wrong with the actual yield you measured in
your experiment.
36