Download e-tcos (2t

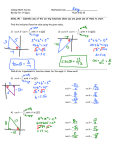
Review Key
1. A 8 lb weight is attached to a spring. It takes a force of 10 lb to stretch the spring 8 feet.
The damping force is approximately half of the velocity. If the mass is pulled 18 inches to the
right of the equilibrium position and given an initial velocity of 3 ft/sec to the left, find the
position function of the mass as well as the amplitude and frequency. Write the position
function in terms of a single cosine function.
Initial conditions:
x(0) = 4/3 feet & x'(0) = 4 ft/sec
Find the spring constant: F = kx »» 10lb = k(8 ft) »» k = 1.25 lb/ft
The differential equation representing the motion is:
mx" + cx' + kx = 0 »»
x" + x' + 1.25x = 0 »»
2
x" + x' + 1.25x = 0
2
»» r + 2r + 5 = 0 »» (r+1) = -4
»» r = -1 ± 2i
»» x = e-t[Acos(2t) + Bsin(2t)]
Since x(0) = 4/3 »» A = 4/3
»» x = e-t[Acos(2t) + Bsin(2t)]
x'(t) = -e-t[Acos(2t) + Bsin(2t)] + e-t[-2Asin(2t) + 2Bcos(2t)]
x'(0) = 4 = -A + 2B
and A = 4/3 »» B = 8/3
»» x(t) = e-tcos(2t) + e-tsin(2t) = e-t[cos(2t) + sin(2t) ]
Now to write as a single trigonometric function: C = √ + = () + () = =
and tan(α) = 2 with cos(α) > 0 & sin(α) > 0 »» α is in Quadrant I
»» α = tan-1(2) = 1.107 and
Time varying amplitude =
√
we have x(t) =
√ -t
e cos
e-2t ft
Period = 2π/2 = π sec
Frequency = 1/π ≈ 0.318 hz
2. Solve the differential equation: y(3) + 125y = 0
Characteristic equation:
r3 +125 = 0 »»
r3 = -125
(2t - 1.107)
√
r3 = 125cisπ »»
r1 = (125cisπ)య = (125)య cis( ) = 5[cos + isin ] = 5( + భ
భ
√
i) = + √
i
Since the roots will have the same modulus and will be equally spaced within 2π we have
ω=
r2 = 5cis( +
) = 5cis(π) = 5[cos(π) + isin(π ) ] = -5
r3 = 5cis(+ ) = 5cis( ) = 5[cos( ) + isin( ) ] =
»» Our solution is: y = c1e-5x + మ [c2cos(
ఱ
√
√
x) + c3sin(
− √
i
x)]
3. Solve the differential equation: y(3) + y" - 2y = xex
Since xex is a UC function we can use the Method of Undetermined Coefficients.
First find yc: the characteristic equation is r3 + r2 - 2r = 0
Using the Rational Zero Theorem we find that the roots are r = 1, r = -1 ± i
and yc = c1ex + [c2cos(x) + c3sin(x)]
Now consider f(x), the nonhomogenous function: f(x) = xex
The typical form of yp = ( A + Bx) ex but since this overlaps with ex in the complementary
solution we must multiply by the appropriate power of x to obtain:
yp = x(A+Bx)ex =(Ax+Bx2) ex
Now, we need to find the derivatives:
(yp)' = (A + 2Bx)ex + (Ax+Bx2) ex = [A + (2B + A)x + Bx2]ex combining the like terms to ease the
differentiation process.
(yp)'' = [(2B + A) + 2Bx]ex + [A + (2B + A)x + Bx2]ex = [(2B+2A) + (4B + A)x + Bx2]ex
(yp)''' = [(4B + A) + 2Bx]ex + [(2B+2A) + (4B + A)x + Bx2]ex = [(6B+3A) +(6B + A)x + Bx2]ex
Now, to substitute into the DE:
[(6B+3A) +(6B + A)x + Bx2]ex + [(2B+2A) + (4B + A)x + Bx2]ex - 2(Ax+Bx2) ex = xex
»» Equating coefficients:
ex-term: (6B+3A) + (2B+2A) = 0 »» 5A + 8B = 0 »» A = − B
xex-term: (6B + A) + (4B + A) - 2A = 1 »» 10B = 1 »» B = and A = − ()= − Finally, yp = ( + x) ex
And, yg = c1ex + [c2cos(x) + c3sin(x)] + (− + x2) ex
4. Use Variation of Parameters to solve the differential equation: y" + 4y' + 4 = e-2xlnx
The characteristic equation: r2 + 4r + 4 = 0 »» (r + 2)2 = 0 and yc = c1e-2x + c2xe-2x
Here we have yp = Ae-2x + Bxe-2x with
y1 = e-2x and y2 = xe-2x so that (y1)' = -2e-2x and (y2)' = e-2x-2xe-2x
Our system of equations we have from the 2 conditions is:
(*) A'e-2x + B'xe-2x = 0
»» Multiplying by 2 »»
-2A'e-2x +B'e-2x-2B'xe-2x=e-2xlnx
»»
2A'e-2x + 2B'xe-2x = 0
-2A'e-2x +B'e-2x-2B'xe-2x=e-2xlnx
Adding these last 2 equations yields: B'e-2x = e-2xlnx »»
»»
B = = xlnx - 1 = xlnx - x
B' = lnx
(**)
Tabular Integration by Parts
u→
u & du
Lnx
dv & v
dx
x
From (*): A'e
-2x
= -B'xe
-2x
du →
»» A' = -B'x
= uv - and using (**)»» A' = -B'x = -xlnx
»» A = −
Again Tabular By Parts
మ
A=
+ − =
మ
Tabular Integration By Parts
+ x2
u→
u & du
Lnx
du →
మ
»» yp = (
←v
dv & v
-x
మ
+ x2)e-2x + (xlnx - x)xe-2x
←v
మ
and yg = yc + yp = c1e-2x + c2x e-2x + (
+ x2)e-2x + (xlnx - x)xe-2x
5. Use Variation of Parameters to solve the differential equation: y" + 4y = csc2(2x)
The characteristic equation: r2 + 4 = 0 »» r = ±2i and yc = c1cos(2x) + c2sin(2x)
Here we have yp = Acos(2x) + Bsin(2x)
and y1 = cos(2x) and y2 = sin(2x) so that (y1)' = -2sin(2x) and (y2)' = 2cos(2x)
Our system of equations we have from the 2 conditions is:
(*) A'cos(2x) + B'sin(2x) = 0 »» Multiplying by 2sin(2x) »
2A'sin(2x)cos(2x) + 2B'sin2(2x) = 0
-2A'sin(2x)+2B'cos(2x)=csc2(2x)» Multiplying bycos(2x) »
-2A'sin(2x)cos(2x)+2B'cos2(2x) = cos(2x) csc2(2x)
Adding these last two equations »» 2B'= csc(2x)cot(2x) »» B' = csc(2x)cot(2x)
»» B = - csc(2x)
»» A =
From (*) we see that A' = -B'tan(2x) = - csc(2x)
ln|csc(2x) - cot(2x)|
and finally:
yp =
()
(
And, yg
ln|csc(2x) - cot(2x)|)
-
= yc + yp = yc = c1cos(2x) + c2sin(2x) +
()
(
ln|csc(2x) - cot(2x)|)
-
6. Use the Series Method to find the power series solution of the form ∑
.
Express in terms of elementary functions.
y" - 4y = 0, y(0) = 2, y'(0) = 0
From the initial conditions we see that c0 = 2 and c1 = 0.
ஶ
௡
௡ିଶ
Subtituting y = ∑ஶ
into the DE:
଴ ௡ and y" = ∑ଶ ( − 1)௡ ௡ିଶ
௡
∑ஶ
- 4∑ஶ
=0
ଶ ( − 1)௡ାଶ ଴ ௡ Re-index the first series
Combining the series
௡
௡
∑ஶ
- 4∑ஶ
=0
଴ ( + 2)( + 1)௡ାଶ ଴ ௡ »»
௡
௡
∑ஶ
଴ [( + 2)( + 1)௡ାଶ − 4௡ ] = 0
»»
Which yields the coefficient recursion formula:
=
n = 0:
, n≥0
()() = ∗ with = 2
Waiting until the end to replace ଴ with 2 for
ease in calculations
n = 1: = ∗ with = 0
We see that all odd-powered terms drop out!
n = 2: = ∗ = ∗ (∗ ) = ∗∗∗ ()మ
n = 4: = ∗ = ∗ (∗∗∗ )=
()మ
()య
!
The coefficient pattern becomes obvious:
=
»» y = [ 2 +
(2)x2 +
!
()೙
!
()మ
!
=
(2)x4 +
()೙
!
()య
!
∗ 2 but with only even powered terms.
(2)x6 + ...] = 2[ 1 + !x2 +
()మ 4
x
!
+
()య 6
x
!
+ ...]
This series looks similar to the cosh(x) series except for the powers of 4 in the numerator.
These can be converted to powers of 2:
y = 2[ 1 +
()మ 2
x
!
+
()ర 4
x
!
+
()ల 6
x
!
+ ...] = 2[ 1 +
()మ
!
+
()ర 4
x
!
+
()ల
!
+ ...] = 2∑ஶ
଴
(2)݊
!
Which is the elementary function: y = 2cosh(2x)
7. Use the Series Method to find the power series solution of the form ∑
.
Express in terms of elementary functions.
y" - 2y' + y = 0, y(0) = 0, y'(0) = 1
From the initial conditions we find: c0 = 0 and c1 = 1.
௡
௡ିଵ
௡ିଶ
Substituting y = ∑ஶ
, y' = ∑ஶ
and y" = ∑ஶ
into the DE:
଴ ௡ ଵ ௡ ଶ ( − 1)௡ ௡ିଶ
௡ିଵ
௡
∑ஶ
- 2∑ஶ
+ ∑ஶ
=0
ଶ ( − 1)௡ ଴ ௡ ଵ ௡ Adjusting the indices of the first two series »»
ஶ
௡
௡
௡
∑ஶ
- ∑ஶ
=0
଴ ( + 2)( + 1)௡ାଶ ଴ 2( + 1)௡ାଵ + ∑଴ ௡ Combining the series »»
௡
௡
∑ஶ
଴ [( + 2)( + 1)௡ାଶ − 2 + 1௡ାଵ + ௡ ]
=0
»»
௡ାଶ = ଶ௖ ି௖
n = 1:
=
n = 2:
=
n = 3:
ଵ
(௡ିଵ)!
ሺ௡ାଶሻ(௡ାଵ)
భ
బ
ଶ = ሺ௡ାଶሻ(௡ାଵ)
=
n = 0:
»» cn =
ଶሺ௡ାଵሻ௖೙శభ ି௖೙
ଶ௖భ
ଶ∗ଵ
, n≥0
=1
=
ଶమ ିଵ
ଵ
ଵ
22 ܿ2 −ܿ1
=
=
=
3∗2
ଷ∗ଶ
ଶ
ଶ!
ଷିଵ
ଶ
ଵ
23ܿ3 −ܿ2
=
= = 4∗3
ସ∗ଷ
ଵଶ
ଷ∗ଶ
2(4)ܿ4−ܿ3
ଵ
5∗4
=
=
ଵ
ଷ!
ସ!
and we have the series
ଵ
ଵ
ଵ
ଵ
ଵ
ଵ
ଶ!
ଷ!
ସ!
ଶ!
ଷ!
ସ!
y = x + x2 + x3 + x4 + x5 + ... = x[ 1 + x + x2 + x3 + x4 + ...] = xex