Download When the rate of change depends upon the amount present we get

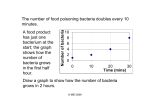
Section 3­8 Exponential Growth and Decay
Examples:
When the rate of change depends upon the amount present we get the following differential equation:
The only solution (something that replaces the y)
is of the form:
P=
Po =
t =
k = relative growth rate
population growth of
people
bacteria, etc
money (continuously compounded interest)
exponential decay
radioactive decay
Newton's law of cooling
Example:
At time zero there are 120 bacteria. After two hours there are 600 bacteria.
a. Find an expression for the number of bacteria at t hours.
b. Find the number of bacteria after 8 hours.
Example:
A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 420.
a. Find an expression for the number of bacteria in t hours.
b. What is the relative growth rate?
c. Find the number of bacteria after 3 hours.
d. Find the rate of growth after 3 hours.
e. When will the population reach 10,000?
Radioactive Decay: using y(t) = y(0)ekt
Note that k is negative for decay. We can write:
m(t) = mass remaining after time t and ­1 dm =k
m dt
Or we have m(t) = m0ekt half life ­ amount of time it takes for ....
from the text: 3­8 #8
Bismuth 210 has a half­life of 5.0 days
a. A sample originally has a mass of 800 mg. Find a formula for the mass remaining after t days.
b. Find the mass remaining after 30 days.
c. When is the mass reduced to 1 mg?
A substance has a half­life of 7 minutes. Find out what fraction of the substance is left after 10 minutes.
Newton's Law of Cooling: The rate of cooling of an object is
proportional to the temperature difference between the object
and its surroundings, provided that this difference is not too
large. (also applies to warming!)
T(t) = temp. of object at time = t
Ts = temp. of the surroundings
Newton's Law as a Differential Equation:
dT = k(T - Ts)
dt
If we let y(t) = (T(t) - Ts) we can use our other formula:
dy = ky
dt
(note that Ts is a constant so y'(t) = T'(t))
See Exercise #14 pg. 240: A thermometer is taken from a room where
the temperature is 20℃ to the outdoors, where the temperature is 5℃.
After one minute the thermometer reads 12℃.
a) What will the reading on the thermometer be after one more minute?
b) When will the thermometer read 6℃?